LightOJ 1319 - Monkey Tradition CRT除数互质版

本题亦是非常裸的CRT。 CRT的余数方程 那么定义

则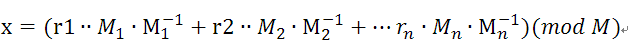

其中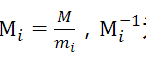
为模mi的逆元。

/** @Date    : 2016-10-23-15.11

  * @Author  : Lweleth (SoungEarlf@gmail.com)

  * @Link    : https://github.com/Lweleth

  * @Version : $

  */

#include <stdio.h>

#include <iostream>

#include <string.h>

#include <algorithm>

#include <utility>

#include <vector>

#include <map>

#include <set>

#include <string>

#include <stack>

#include <queue>

#define LL long long

#define MMF(x) memset((x),0,sizeof(x))

#define MMI(x) memset((x), INF, sizeof(x))

using namespace std;



const int INF = 0x3f3f3f3f;

const int N = 1e5+2000;



LL r[16];

LL p[16];

LL gcd(LL a, LL b)

{

    return b?gcd(b, a % b):a;

}

LL exgcd(LL a, LL b, LL &x, LL &y)

{

    LL d = a;

    if(!b)

    {

        x = 1;

        y = 0;

    }

    else

    {

        d = exgcd(b , a % b, y, x);

        y -= (a / b) * x;

    }

    return d;

}

LL Inv(LL a, LL b)//exgcd求逆元

{

    LL g = gcd(a, b);

    if(g != 1)

        return -1;

    LL x, y;

    exgcd(a, b, x, y);

    return (x % b + b) % b;

}

//x--= (r1*M1*(M1^-1)+r2*M2*(M2^-1)…rn*Mn*(Mn^-1)) mod M;

//M 是所有互素p的乘积 Mi 是 M/p[i]

//M^-1是 模 p[i]的逆元

LL CRT(LL *r, LL *p, int n)

{

    LL M = 1;

    LL ans = 0;

    for(int i = 0; i < n; i++)

    {

        M *= p[i];

    }

    for(int i = 0; i < n; i++)

    {

        LL x, y;

        LL Mi = M / p[i];

        ans = (ans + r[i] * Mi * Inv(Mi, p[i])) % M;

    }

    if(ans < 0)

        ans += M;

    return  ans;

}

int main()

{

    int T;

    int cnt = 0;

    cin >> T;

    while(T--)

    {

        int n;

        scanf("%d", &n);

        for(int i = 0; i < n; i++)

        {

            scanf("%lld%lld", p + i, r + i);

        }

        LL ans = CRT(r, p, n);

        printf("Case %d: %lld\n", ++cnt, ans);

    }

    return 0;

}