Codeforces 450B div.2 Jzzhu and Sequences 矩阵快速幂or规律
Jzzhu has invented a kind of sequences, they meet the following property:
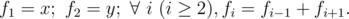
You are given x and y, please calculate fn modulo 1000000007 (109 + 7).
Input
The first line contains two integers x and y (|x|, |y| ≤ 109). The second line contains a single integer n (1 ≤ n ≤ 2·109).
Output
Output a single integer representing fn modulo 1000000007 (109 + 7).
Examples
input
2 3
3
output
1
input
0 -1
2
output
1000000006
Note
In the first sample, f2 = f1 + f3, 3 = 2 + f3, f3 = 1.
In the second sample, f2 = - 1; - 1 modulo (109 + 7) equals (109 + 6).
题意:给出一个递推式和前两项,求第n项模1e9+7后的值。
题解:这题其实本来是很水的..只是最近都在尝试写一些矩阵快速幂的题目,最难的在于化递推式并构造矩阵上,而这道题直接给出了递推式,心痒想使用矩阵。_(:3」∠)_
由f(i)=f(i+1)+f(i-1)可以得出f(i+1)=f(i)-f(i-1)
又由于i>=2,从f(1)开始,于是
f(3)=(1) * f(2) + (-1) * f(1)
f(2)=(1) * f(1) + (0) * f(0)
另外要注意的是,得到的值是负数还得再处理一下。(最近总WA在这上)
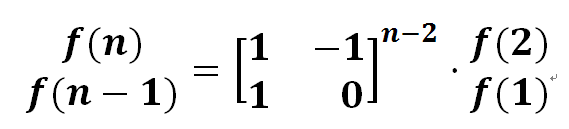
1 #include <stdio.h>
2 #include <algorithm>
3 #include <iostream>
4 #include <string.h>
5 #define ll __int64
6 using namespace std;
7
8 const int mod = 1000000007;
9 struct matrix
10 {
11 ll x[2][2];
12 };
13 matrix mul(matrix a, matrix b)
14 {
15 matrix c;
16 c.x[0][0] = c.x[0][1] = c.x[1][0] = c.x[1][1] = 0;
17 for( int i = 0; i < 2; i++)
18 for(int j = 0; j < 2; j++)
19 {
20 for(int k = 0; k < 2; k++)
21 {
22 c.x[i][j] += a.x[i][k] * b.x[k][j];
23 }
24 c.x[i][j] %= mod;
25 }
26 return c;
27 }
28 matrix powe(matrix x, ll n)
29 {
30 matrix r;
31 r.x[1][1] = r.x[0][0] = 1; //注意初始化
32 r.x[0][1] = r.x[1][0] = 0;
33 while(n)
34 {
35 if(n & 1)
36 r = mul(r , x);
37 x = mul(x , x);
38 n >>= 1;
39 }
40 return r;
41 }
42 int main()
43 {
44
45 ll x, y, n, ans;
46 while(~scanf("%I64d%I64d%I64d", &x, &y, &n))
47 {
48 if(n == 2)
49 printf("%I64d\n",(y%mod + mod)%mod); //负数情况下的考虑
50 else if(n == 1)
51 printf("%I64d\n",(x%mod + mod)%mod);
52 else
53 {
54 matrix d;
55 d.x[0][0] = 1;
56 d.x[0][1] = -1;
57 d.x[1][0] = 1;
58 d.x[1][1] = 0;
59
60 d = powe(d, n - 2);
61 ans = d.x[0][0] * y +d.x[0][1]*x;
62 printf("%I64d\n", (ans%mod+mod)%mod );
63 }
64
65 }
66 }





