决策树算法系列之一 ID3

1 什么是决策树

• 通俗来说，决策树分类的思想类似于找对象
• 一个女孩的母亲要给这个女孩介绍男朋友 (分类问题、见或不见)
• 女孩有自己的一套标准

长相	收入	职业	见面与否
丑	高	某箭队经理	不见
中等	低	某大学学生会主席	不见
中等	中等	某NN记者	不见
中等	高	某上市公司CTO	见
帅	中等	公务员	见

       那么有下面的对话

       女儿：长的帅不帅？
       母亲：挺帅的。
       女儿：收入高不？
       母亲：不算很高，中等情况。
       女儿：是公务员不？
       母亲：是，在税务局上班呢。
       女儿：那好，我去见见。

2 决策树的做法

       每次选择一个属性进行判断， 若不能得出结论，继续选择其
他属性进行判断，直到能够“肯定地”判断

       长相 -> 收入 -> 职业

       如何让机器学习到这种有递进关系、且考虑有优先顺序属性像树结构的分类方法？

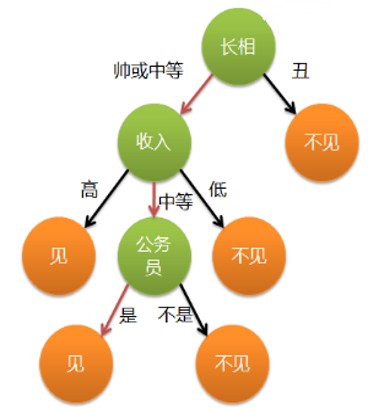
图1 一颗简单的决策树

3 决策树的构建

• 步骤1：将所有的数据看成是一个节点，进入步骤2；
• 步骤2：从中挑选一个数据特征对节点进行分割，进入步骤3；
• 步骤3：生成若干孩子节点，对每一个孩子节点进行判断若满足停止分裂的条件，进入步骤4；否则，进入步骤2；
• 步骤4：设置该节点是子节点，其输出为该节点数量占比最大的类别。

       所以有三个问题:
       (1) 数据如何分割
       离散型数据的分割
       连续型数据的分割

       (2)如何选择分裂的属性
       分裂算法（ID3 C4.5 CART)

       (3)什么时候停止分裂
       最小节点数、树深度、所有特征已经使用完毕

4 一个做分类的数据集

天气	温度	湿度	是否有风	是否室内打网球
晴	热	高	否	否
晴	热	高	是	否
阴	热	高	否	是
雨	温	高	否	是
雨	凉爽	中	否	是
雨	凉爽	中	是	否
阴	凉爽	中	是	是
晴	温	高	否	否
晴	凉爽	中	否	是
雨	温	中	否	是
晴	温	中	是	是
阴	温	高	是	是
阴	热	中	否	是
雨	温	高	是	否

5 ID算法

       训练集为D, 总样本数|D|
       训练集中有N个类别，|Ci|为第i个类别的数量
       假设其中一个属性A有n个不同离散取值(a1,a2…an)
       假设取值a1样本集为Da1，个数为|Da1|，其中属于第j个类的个数为|Da1,j |
       假设取值a2样本集为Da2，个数为|Da2|，其中属于第j个类的个数为|Da2,j|
       …
       假设取值an样本集为Dan，个数为|Dan|，其中属于第j个类的个数为|Dan,j|

       (1) 计算数据集D的经验熵

\[H\left( D \right) = - \sum\limits_{i = 1}^N {\frac{{\left| {{C_i}} \right|}}{{\left| D \right|}}} \log \frac{{\left| {{C_i}} \right|}}{{\left| D \right|}} \]

       (2) 计算属性A对数据集D的经验条件熵

\[H\left( {D\left| A \right.} \right) = \sum\limits_{i = 1}^n {\frac{{\left| {{D_{ai}}} \right|}}{{\left| D \right|}}} H\left( {{D_{ai}}} \right) = \sum\limits_{i = 1}^n {\left( {\frac{{\left| {{D_{ai}}} \right|}}{{\left| D \right|}}\left( { - \sum\limits_{j = 1}^N {\frac{{\left| {{D_{ai,j}}} \right|}}{{\left| {{D_{ai}}} \right|}}\log \frac{{\left| {{D_{ai,j}}} \right|}}{{\left| {{D_{ai}}} \right|}}} } \right)} \right)} \]

       (3) 计算属性A信息增益

\[G\left( {D\left| A \right.} \right){\rm{ = }}H\left( D \right) - H\left( {D\left| A \right.} \right) \]

       选择使得G(D|A）最大的属性A作为最优属性进行决策划分

6 具体实例

       (1) 计算数据集D的经验熵
       一共14个样本，9个正例、5个负例

\[H\left( D \right) = - \left( {\frac{{\rm{9}}}{{{\rm{14}}}}\log \frac{{\rm{9}}}{{{\rm{14}}}}{\rm{ + }}\frac{{\rm{5}}}{{{\rm{14}}}}\log \frac{{\rm{5}}}{{{\rm{14}}}}} \right){\rm{ = }}0.2830 \]

       (2) 计算属性对数据集D的经验条件熵 (天气属性)
       天气一共有晴、阴、雨三个属性
       天气 =晴 , 2个正例、3个负例,所以

\[H\left( {D\left| {{A_晴}} \right.} \right) = - \left( {\frac{2}{5}\log \frac{2}{5}{\rm{ + }}\frac{3}{5}\log \frac{3}{5}} \right){\rm{ = }}0.{\rm{2923}} \]

       天气 =阴, 4个正例、0个负例, 所以

\[H\left( {D\left| {{A_阴}} \right.} \right) = - \left( {\frac{4}{4}\log \frac{4}{4}{\rm{ + }}\frac{0}{4}\log \frac{0}{4}} \right){\rm{ = 0}} \]

       天气 =雨, 3个正例、2个负例,所以

\[H\left( {D\left| {{A_雨}} \right.} \right) = - \left( {\frac{3}{5}\log \frac{3}{5}{\rm{ + }}\frac{2}{5}\log \frac{2}{5}} \right){\rm{ = }}0.{\rm{2923}} \]

       所以天气属性的经验条件熵为

\[H\left( {D\left| A \right.} \right) = \frac{{\rm{5}}}{{{\rm{14}}}} \cdot 0.{\rm{2923 + }}\frac{{\rm{4}}}{{{\rm{14}}}} \cdot {\rm{0 + }}\frac{{\rm{5}}}{{{\rm{14}}}} \cdot 0.{\rm{2923 = }}0.{\rm{2}}0{\rm{87}} \]

       (3) 天气属性的信息增益

\[G\left( {D\left| A \right.} \right) = H\left( D \right) - H\left( {D\left| A \right.} \right) = 0.0{\rm{743}} \]

       同理可以算出温度、湿度、是否有风的信息增益

属性	信息增益
天气	0.0743
温度	0.0088
湿度	0.0457
是否有风	0.0145

       因此天气的信息增益最大，决策树第一个决策节点选择天气进行决策即有:

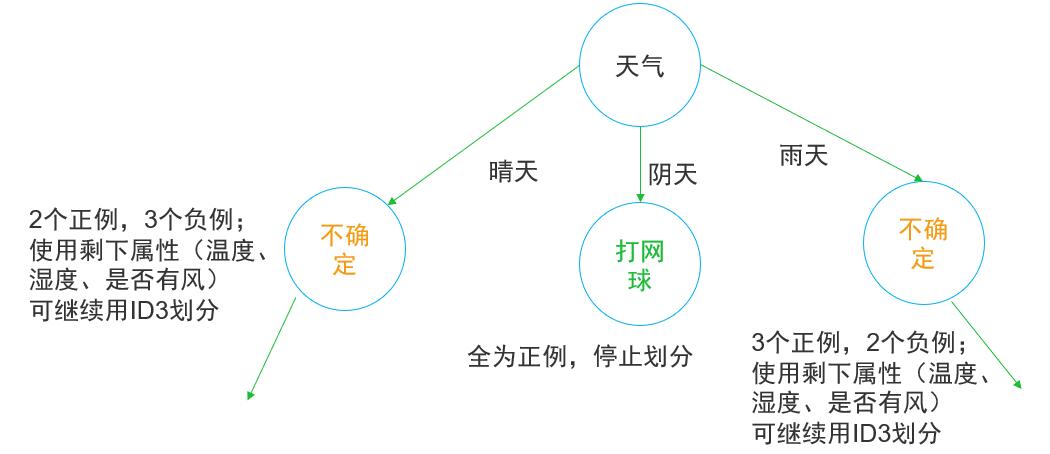
图2 决策树节点划分