机器学习是时下流行AI技术中一个很重要的方向,无论是有监督学习还是无监督学习都使用各种“度量”来得到不同样本数据的差异度或者不同样本数据的相似度。良好的“度量”可以显著提高算法的分类或预测的准确率,本文中将介绍机器学习中各种“度量”,“度量”主要由两种,分别为距离、相似度和相关系数,距离的研究主体一般是线性空间中点;而相似度研究主体是线性空间中向量;相关系数研究主体主要是分布数据。本文主要介绍距离。
1 向量距离
1.1 欧式距离¬——从勾股定理而来
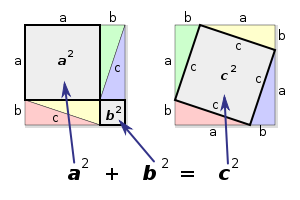
让我回忆一下中学时候学过的勾股定理,历史悠久的勾股定理告诉了如果在一个直角三角形中两条直角边分别为\(a\)和\(b\),那么斜边\(c\)和\(a\)、\(b\)的关系一定满足\(c^{2} = a^{2} + b^{2}\)
![]()
图1 勾股定理
![]()
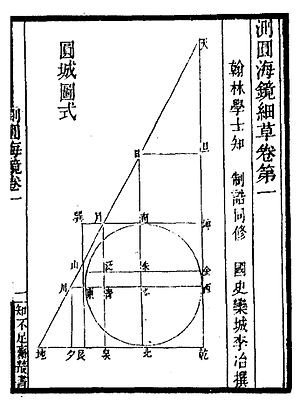
图2 成书于宋金时期《测圆海镜》中的十五个勾股形
从直观上将,图2中两个点距离是蓝线的长度,而使用勾股定理可以计算出如图2的两个数据点之间距离。
![]()
图3 可汗学院距离教程中样例
根据勾股定理很容易求出上面两个点距离为如下式子表示:
![]()
这个最直观的距离还有一个正式称呼,欧几里得距离(Euclidean distance),上面是二维空间中欧式距离,更为一般的情况为:在笛卡尔坐标系(Cartesian Coordinates)中如果点x = (x1, x2,..., xn) 和点 y = (y1, y2, ..., yn) 是两个欧式空间的点,则点x和点y的欧式距离为:
\[\begin{array}{l}
{d_{Euclidean}}\left( {x,y} \right){\rm{ = }}{d_{Euclidean}}\left( {y,x} \right) = \sqrt {{{\left| {{x_1} - {y_1}} \right|}^2} + {{\left| {{x_2} - {y_2}} \right|}^2} + \cdots + {{\left| {{x_n} - {y_n}} \right|}^2}} \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; = \sqrt {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^2}} } \\
\end{array}\]
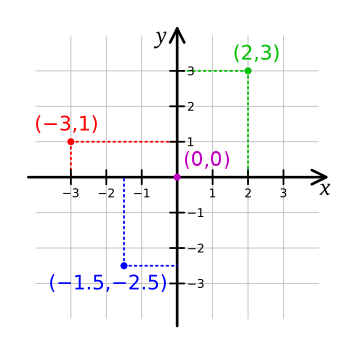
笛卡尔坐标系: 一种正交坐标系。参阅图4,二维的直角坐标系是由两条相互垂直、相交于原点的数线构成的。在平面内,任何一点的坐标是根据数轴上对应的点的坐标设定的
![]()
图4 一个直角坐标系
1.2 曼哈顿距离¬¬——行走在纽约曼哈顿街道上
曼哈顿距离(Manhattan distance)是由十九世纪的赫尔曼·闵可夫斯基所创辞汇,用以标明两个点上在标准坐标系上的绝对轴距之总和。例如在平面上,坐标(x1, x2)的点P1与坐标(y1, y2)的点P2的曼哈顿距离为:
\[\left| {{x_1} - {y_1}} \right| + \left| {{x_2} - {y_2}} \right|
\]
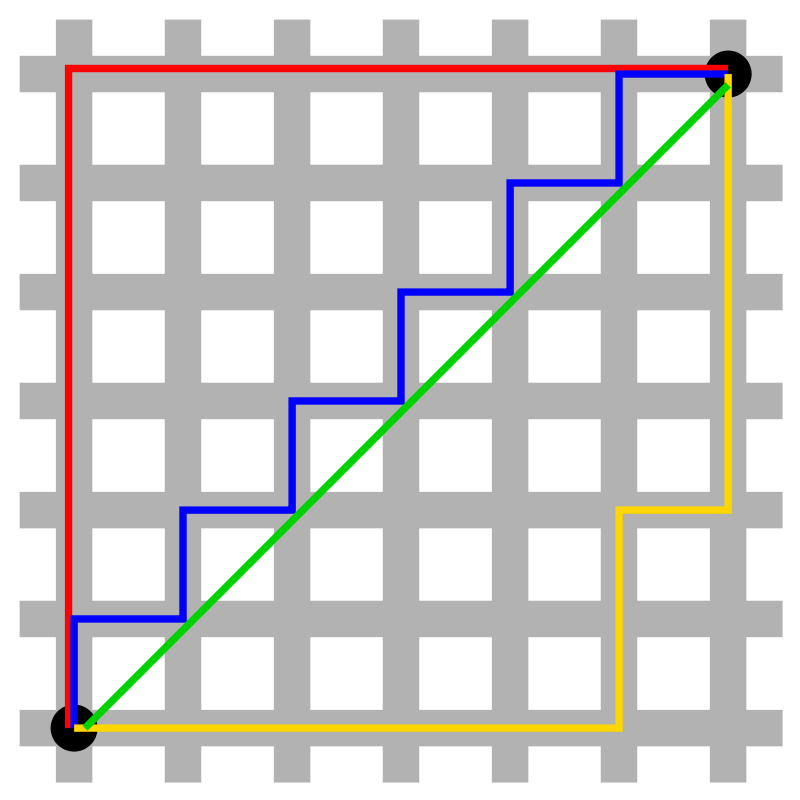
如图所示为曼哈顿与欧几里得距离。由曼哈顿距离和欧式距离定义可知两点曼哈顿距离为12,其中红、蓝与黄线分别表示几种不同曼哈顿距离;两点的欧式距离为6√2其中绿线表示唯一的欧几里得距离。
![]()
图5 曼哈顿与欧几里得距离
![]()
图6 到蓝点的曼哈顿距离为2的所有点构成的“单位圆”
上面是二维空间中曼哈顿距离,更为一般的情况为:在笛卡尔坐标系中如果点x = (x1, x2,..., xn) 和点 y = (y1, y2, ..., yn) 是两个欧式空间点,则点x和点y的曼哈顿距离为:
\[\begin{array}{l}
{d_{Manhat\tan }}\left( {x,y} \right){\rm{ = }}{d_{Manhat\tan }}\left( {y,x} \right) = \left| {{x_1} - {y_1}} \right| + \left| {{x_2} - {y_2}} \right| + \cdots + \left| {{x_n} - {y_n}} \right| \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; = \sum\limits_{i = 1}^n {\left| {{x_i} - {y_i}} \right|} \\
\end{array}\]
1.3 切比雪夫距离——来下盘国际象棋吧
切比雪夫距离(Chebyshev distance)或是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值]。切比雪夫距离得名自俄罗斯数学家切比雪夫。例如在平面上,坐标(x1, x2)的点P1与坐标(y1, y2)的点P2的切比雪夫距离为:
\[\max \left( {\left| {{x_1} - {y_1}} \right|,\left| {{x_2} - {y_2}} \right|} \right)
\]
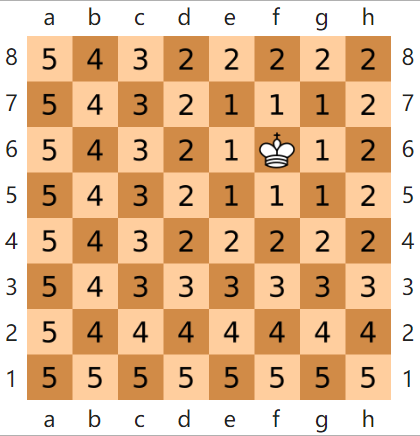
若将国际象棋棋盘放在二维直角座标系中,格子的边长定义为1,座标的x轴及y轴和棋盘方格平行,原点恰落在某一格的中心点,则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离,因此切比雪夫距离也称为棋盘距离。由于王可以往斜前或斜后方向移动一格,因此可以较有效率的到达目的的格子。例如位置F6和位置E2的切比雪夫距离为4。任何一个不在棋盘边缘的位置,和周围八个位置的切比雪夫距离都是1。
![]()
图7 国际象棋棋盘上二个位置间的切比雪夫距离
上面是二维空间中切比雪夫距离,更为一般情况为:在笛卡尔坐标系中如果点x = (x1, x2,..., xn) 和点 y = (y1, y2, ..., yn) 是两个欧式空间点,则点x和点y切比雪夫距离为:
1.4 闵科夫斯基距离¬——大统一论
闵科夫斯基距离(Minkowski distance)实际上是欧式距离、曼哈顿距离、切比雪夫距离在笛卡尔坐标系下的一种推广,闵科夫斯基距离将上述所以距离都统一在一个框架中。在笛卡尔坐标系中如果点x = (x1, x2,..., xn) 和点 y = (y1, y2, ..., yn)是两个欧式空间点,则点x和点y的p阶闵科夫斯基距离为:
\[\begin{array}{l}
{d_{p - Minkowski}}\left( {x,y} \right){\rm{ = }}{d_{p - Minkowski}}\left( {y,x} \right) = {\left( {{{\left| {{x_1} - {y_1}} \right|}^p} + {{\left| {{x_2} - {y_2}} \right|}^p} + \cdots + {{\left| {{x_n} - {y_n}} \right|}^p}} \right)^{\frac{1}{p}}} \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; = {\left( {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^p}} } \right)^{\frac{1}{p}}} \\
\end{array}\]
当p=1的时候,1阶闵科夫斯基距离等价于曼哈度距离
\[\begin{array}{l}
{d_{1 - Minkowski}}\left( {x,y} \right){\rm{ = }}{d_{1 - Minkowski}}\left( {y,x} \right) = {\left( {{{\left| {{x_1} - {y_1}} \right|}^1} + {{\left| {{x_2} - {y_2}} \right|}^1} + \cdots + {{\left| {{x_n} - {y_n}} \right|}^1}} \right)^{\frac{1}{1}}} \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\;\;\;\;\; = \sum\limits_{i = 1}^n {\left| {{x_i} - {y_i}} \right|} \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\;\;\;\;\; = \left| {{x_1} - {y_1}} \right| + \left| {{x_2} - {y_2}} \right| + \cdots + \left| {{x_n} - {y_n}} \right| \\
\end{array}\]
当p=2的时候,2阶闵科夫斯基距离等价于欧几里得距离
\[\begin{array}{l}
{d_{2 - Minkowski}}\left( {x,y} \right){\rm{ = }}{d_{2 - Minkowski}}\left( {y,x} \right) = {\left( {{{\left| {{x_1} - {y_1}} \right|}^2} + {{\left| {{x_2} - {y_2}} \right|}^2} + \cdots + {{\left| {{x_n} - {y_n}} \right|}^2}} \right)^{\frac{1}{2}}} \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\;\;\;\;\; = \sqrt {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^2}} } \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\;\;\;\;\; = \sqrt {{{\left| {{x_1} - {y_1}} \right|}^2} + {{\left| {{x_2} - {y_2}} \right|}^2} + \cdots + {{\left| {{x_n} - {y_n}} \right|}^2}} \\
\end{array}\]
当p=∞的时候,∞阶闵科夫斯基距离等价于车比雪夫距离
\[\begin{array}{l}
{d_{\infty - Minkowski}}\left( {x,y} \right){\rm{ = }}{d_{\infty - Minkowski}}\left( {y,x} \right) = \mathop {\lim }\limits_{x \to \infty } {\left( {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^p}} } \right)^{\frac{1}{p}}} \\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\;\;\;\;\; = \max \left( {\left| {{x_1} - {y_1}} \right|,\left| {{x_2} - {y_2}} \right|, \cdots ,\left| {{x_n} - {y_n}} \right|} \right) \\
\end{array}\]

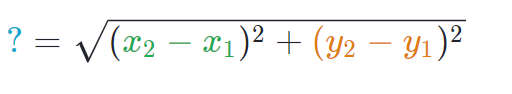



 浙公网安备 33010602011771号
浙公网安备 33010602011771号