「模拟赛」NOIP2024 模拟 2
Rank 14，190 pts
新的阶乘
容易发现只需要处理 1~n 的质因子分解即可，每个数 \(i\) 本来有 \(n-i+1\) 个
我们在欧拉筛的过程中同时维护每个数的一个质因子 \(pri\)
每次从 \(n\) 到 1 把遇到的非质数 \(i\) 现有的个数加到他的质因子 \(pri_i\) 和 \(\frac{i}{pri_i}\) 上
这样最后只会剩下质数里是有数的，就是答案
code
#include<bits/stdc++.h>
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type int
#define qr(x) x=read()
typedef long long ll;
using namespace std;
inline Type read(){
char c=getchar(); Type x=0, f=1;
while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();
while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();
return x*f;
}
const int N = 1e7 + 5;
const int M = 7e5 + 5;
int n, pri[M], a[N], cnt;
bool ifpri[N]; ll num[N], f[N];
int nxt[N], to[N];
inline void Euler(){
for(int i=2; i<=n; i++){
if(!a[i]){
pri[++cnt] = i;
a[i] = i;
}
for(int j=1; j<=cnt; j++){
if(1ll * i * pri[j] > n or pri[j] > a[i]) break;
a[i*pri[j]] = pri[j];
}
}
for(int i=1; i<=cnt; i++)
ifpri[pri[i]] = true, nxt[pri[i]] = pri[i+1];
}
signed main(){ // factorial
Aqrfre(factorial, factorial);
qr(n); Euler();
for(int i=2; i<=n; i++) num[i] = n - i + 1;
for(int i=n; i>=2; i--){
if(ifpri[i]) continue;
num[a[i]] += num[i]; num[i/a[i]] += num[i];
}
cout<<"f("<<n<<")"<<"=";
for(int i=1; i<=cnt; i++){
if(i != 1) cout<<"*";
cout<<pri[i];
if(num[pri[i]] > 1) cout<<"^"<<num[pri[i]];
}
return 0;
}
博弈树
先放下好说的结论：起点作根时，如果以起点作为一个端点的所有最长链都在这个点的一颗子树内，则先手必胜，否则先手必败
证明如下：
-
先手必败：如下图，发现先手跳到 1 号点，那么后手一定可以绕过跟跳到 3 号点；若跳到 2 号点或者 5 号点，后手可以跳到 4 号点
后手一定可以跳到跨过根节点的和先手对称的点，所以只要先手能跳后手就能跳
-
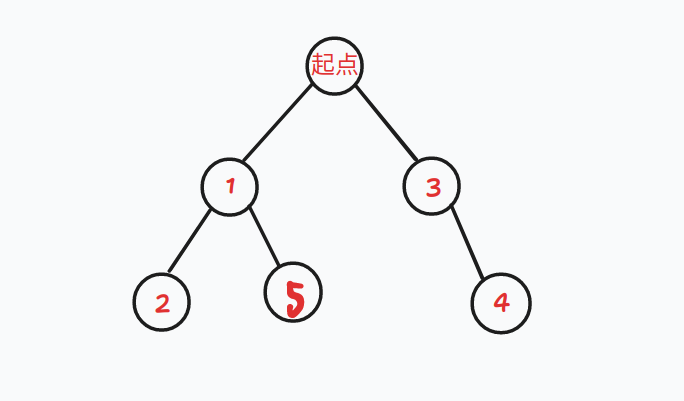
先手必胜：如下图，先手直接跳到 1 号点，此时如果后手继续向下跳的话相当于先后手互换，仍同以上情况（互换后的先手必败）；
而若后手向上走到 3 号点，先手再走到 4 号点便可以让后手无路可走，所以先手必胜。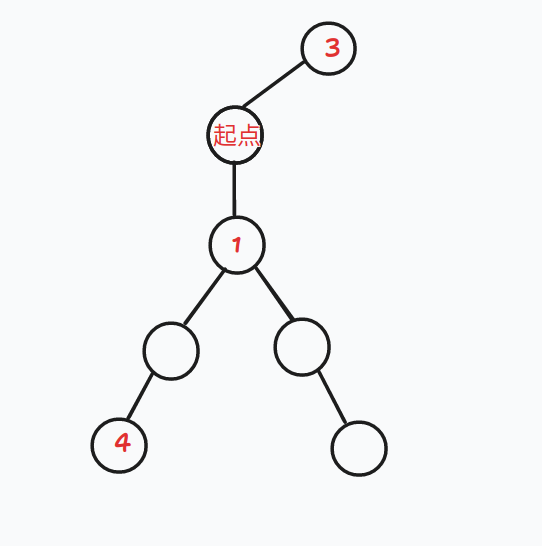
发现以上结论等价于如下：
- 树只有一个重心的时候，只有重心的位置有后手胜，其余都是先手胜；
- 树有两个重心的时候，全是先手胜。
划分
考虑两种情况：
-
前 \(k\) 位没有 1：那么一定是从第一个 1 开始到最后为一段，第一个 1 之前的数（设有 \(q\) 个）分成至少 \(k-1\) 段，方案数用插板法易得为 \(\sum_{i=k-1}^qC_{q-1}^{i-1}\)
-
前 \(k\) 位有 1：那么最优答案一定是最高位为 1 且共有 \(n-k+1\) 位，也就是说选出组合起来的值最大的 \(n-k+1\) 作为一段，其余的分成 \(k-1\) 段长度为 1 的；
易证：前 \(k\) 位有 1，所以可以做到有 \(n-k+1\) 位的数最高位为 1，此时若位数减少一位，则原数左移一位，至少减少 1，减去的那一位若是一，最多增加 1，所以直接选 \(n-k+1\) 位一定不劣
所以可以用最“大”表示法或者二分哈希（下文中细说）找出长度为 \(n-k+1\) 的值最大的字符串，方案数也是哈希找出从高到低前 \(n-k\) 位与这个数相等的个数。
为什么是前 \(n-k\) 位：若最大值第 \(n-k+1\) 位为 0，则前 \(n-k\) 位相等两数一定相同；若最大值第 \(n-k+1\) 位为 1，则前 \(n-k\) 位相同，无论第 \(n-k\) 位是不是 1，这种划分也一定是最优的，因为第 \(n-k\) 位是 1 对答案的贡献增加 1，不是 1 它也会以自己成一段的方式对答案贡献 1.
二分哈希：枚举起点，维护当前找到的值最大的起点，二分找到 当前枚举的起点构成的字符串 和 值最大的起点构成的字符串 第一个不一样的位，判断大小即可判断出两个字符串的大小
