Noip 复习 知识点 + trick
updated on 11.28，Noip2024 考前前两天：明天就出发秦皇岛了，今天复习复习板子
杂项
筛法
线性筛：
线性复杂度筛出所有素数
核心思想：为了防止重复筛一个数，我们让一个数只被它最小的素数筛去
int pri[N], vis[N], cnt; //pri 存所有质数
for(int i=2; i<=n; i++){
if(!vis[i]) pri[++cnt] = i; //未被筛出去则是素数
for(int j=1; j<=cnt&&pri[j]*i<=n; j++){
vis[i*pri[j]] = true;
if(i % pri[j] == 0) break; //如果 i 是 pri[j] 的倍数，则 i 的所有乘积也都是其倍数，所以被它筛过了
}
}
二维数点（二维偏序）
【模板】问题：在一段区间 \([l, r]\) 内查询小于等于 \(x\) 的元素数量。
考虑前缀和的思想，实际上答案就是 \([1,r]\) 区间内小于等于 \(x\) 的元素数量 减去 \([1,l-1]\) 小于等于 \(x\) 的元素数量
所以直接离线维护权值线段树或树状数组，从左到右依次加入序列中元素，并在需要的时候统计答案
主函数核心代码如下：
for(int i=1; i<=m; i++){
int qr(l), qr(r), qr(x);
v[l-1].emplace_back( mp(x, mp(i, -1)) );
v[r].emplace_back( mp(x, mp(i, 1)) );
}
for(int i=1; i<=n; i++){
t.update(1, 1, n, a[i]);
for(auto A : v[i])
ans[A.th2.th1] += t.query(1, 1, n, A.th1) * A.th2.th2;
}
————11.20
图论
tarjan
求强连通分量，点双连通分量，边双连通分量，割点，割边
说到 tarjan，肯定要推一推这篇前无古人后无来者的简练详细的博客，初学看得懂，复习也够简练
这里就只放求强连通分量代码了
int th, top, scc; //分别表示 dfs 的时间戳、栈顶、强连通分量个数
int s[N], ins[N]; //s 为手写栈，ins[i] 表示 i 这个点是否在栈中
int low[N], dfn[N], belong[N]; //belong[i] 表示 i 这个点所属的强连通分量的标号
void tarjan(int x){
low[x] = dfn[x] = ++th;
s[++top] = x, ins[x] = true;
for(int i=head[x]; i; i=nxt[i]){ //链式前向星存边
int y = to[i];
if(!dfn[y]){ //若 y 还没被搜索过
tarjan(y); // 搜索 y
low[x] = min(low[x], low[y]);
}
else if(ins[y]){ // y 在栈中
low[x] = min(low[x], dfn[y]);
}
}
if(low[x] == dfn[x]){
++scc;
do{ //将栈中从 x 到栈顶所有元素取出
belong[s[top]] = scc;
ins[s[top]] = false;
}while(s[top--] != x);
}
}
数据结构
ST 表
利用倍增思想，可以做到 \(O(n\log)\) 预处理 \(O(1)\) 查询，如询问区间最大值、最小值等
详见 ST表详解(稀疏表)
查询大致原理如图：
蓝线长度为 \(2^{\lfloor log_2(r-l+1)\rfloor}\)，显然大于 \(\frac{(r-l+1)}2\)，所以这两条蓝线可以做到覆盖整个区间
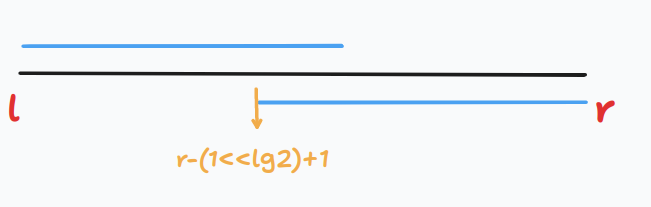
倍增预处理：
for(int j=1; j<=18; j++){
for(int i=1; i<=n; i++)
stmax[j][i] = max(stmax[j-1][i], stmax[j-1][i+(1<<j-1)]),
stmin[j][i] = min(stmin[j-1][i], stmin[j-1][i+(1<<j-1)]);
}
查询：
inline int getmax(int l, int r){
int lg2 = log2(r-l+1);
return max(stmax[lg2][l], stmax[lg2][r-(1<<lg2)+1]);
}
inline int getmin(int l, int r){
int lg2 = log2(r-l+1);
return min(stmin[lg2][l], stmin[lg2][r-(1<<lg2)+1]);
}
题：
abc352D Permutation Subsequence
——写于 11.7
STL
map
注意到 map 查询一次的复杂度在 \(O(\log)\) 左右，一般推荐使用 unordered_map。 大多数情况为 \(O(1)\)，但可以构造的哈希冲突可以卡到 \(O(n)\)，所以有以下 pbds 中的两个解决哈希冲突的哈希表 gp_hash_table、cc_hash_table，可以去下文阅读。
而如果我们只需要查询一个元素 \(key\) 是否在 map 数组 t 里出现过的话，可以使用比 if(t[key]) 较快一些的 count 或者 find 函数
函数 count()：
返回容器中一个元素出现的次数。而在 map 中，一个元素只有 有或没有 两种情况，所以返回值只能为 1/0，表示是否出现过。
map<int>t;
int num = t.count(3); //num 为 1/0 表示 3 出现的次数
函数 find()：
返回的是被查找元素的指针位置，没有则返回 map.end()
要判断某一个 \(key\) 是否出现过：
if(t.find(key) != t.end()) cout<<"出现过";
vector （去重、离散化）
离散化：
只介绍一种常用的去重方法，时间复杂度 \(O(n\log )\)，当然也有一些别的如自带函数的实现方法，详见 C++ 给vector去重的三种方法
排序加去重：
-
排序
-
找重，
auto it = unqiue(v.begin(), v.end());：把 vector 数组中重复的元素堆到最后，返回的是堆到后面的第一个重复元素的指针 -
erase函数，erase(it, v.end());：删除指针为it开始一直删到最后
sort(v.begin(), v.end());
erase(unique(v.begin(), v.end()), v.end()); //去重
pbds
比 STL 还 STL ！
也叫做平板电视 Here，内含比 map 快很多的哈希表，甚至平衡树？！
封装了 hash、tree、trie、priority_queue 这四种数据结构
需要万能拓展库头文件 #include<bits/extc++.h>
以及 using namespace __gnu_pbds;
内带哈希表：如：gp_hash_table<int, int>、cc_hash_table<int, int>
gp 和 cc 的对比： 一般是 cc_hash_table 较快，gp 采用 探测法，cc 采用 拉链法。
C++ 中的 map, unordered_map, cc_hash_table, gp_hash_table 简记
——写于 11.7
updated on 11.13，更新了 gp 和 cc 的实现方式 并添加了两篇资料
字符串算法
manacher
马拉车算法（ ，OI-Wiki
算法介绍： 线性复杂度内找出以每个字符为回文中心的最长回文半径
存下模板代码（只用于求奇数回文）：
int l = 0, r = -1;
for(int i=1; i<=n; i++){
int k = i > r ? 1 : min(d[l+r-i], r-i+1);
while(i - k > 0 and k + i <= n and s[i-k] == s[i+k]) k++;
d[i] = k--;
if(r < i + k) l = i - k , r = i + k;
}
偶数回文：直接把原字符串每相邻两个字符之间加上一个特殊字符就避免了偶数回文的情况，如 #
当时自己推的板子是个什么构思？？
板子题： 【模板】manacher
code
#include<bits/stdc++.h>
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type ll
#define qr(x) x=read()
typedef __int128 INT;
typedef long long ll;
using namespace std;
inline ll read(){
char c=getchar(); ll x=0, f=1;
while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();
while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();
return x*f;
}
const int N = 2.2e7 + 10;
int n, d[N];
char in[N], s[N];
signed main(){ // a
// Aqrfre(a, a);
cin>>(in+1); n = strlen(in+1);
int cnt = 0;
for(int i=1; i<=n; i++)
s[++cnt] = '@', s[++cnt] = in[i];
s[++cnt] = '@'; n = cnt;
int l = 0, r = -1, ans = 0;
for(int i=1; i<=n; i++){
int k = i > r ? 1 : min(d[l+r-i], r-i+1);
while(i - k > 0 and k + i <= n and s[i-k] == s[i+k]) k++;
d[i] = k--;
if(r < i + k) l = i - k , r = i + k;
}
for(int i=1; i<=n; i++){
if(s[i] == '@') ans = max(ans, d[i] / 2 * 2);
else ans = max(ans, d[i] - !(d[i] & 1));
}
cout<<ans<<"\n";
return 0;
}
最小表示法
用于解决： 有一个字符串，这个字符串的首尾是连在一起的，要求寻找一个位置，以该位置为起点的字符串的字典序在所有的字符串中中最小。
考虑在 外层枚举起点 内层遍历以该起点打头的字符串 的基础上进行优化。如果两个字符串分别是从 \(i\) 位置和 \(j\) 位置打头的，并且有 \(s_{[i,i+k)}=s_{[j,j+k)}\)，而 \(s_{i+k}\neq s_{j+k}\)，那么若 \(s_{i+k}>s_{j+k}\)，则显然的有 \([i,i+k)\) 位置上的字符都不可以作为要找的位置；否则也同理。那么这样我们内层遍历了多大的长度，下一次外层枚举的时候就可以忽略这么多的长度，保证时间复杂度为 \(O(n)\) 的。
解释一下为什么 k==n 的时候 break，发现这种情况整个字符串是会存在循环节的，并且以循环节的每一个字符为开头都做过一遍了
模板代码：
int k = 0, i = 1, j = 2;
while(i <= n and j <= n){
for(k=0; k<n; k++)
if(in[i+k] != in[j+k]) break;
if(k == n) break;
if(in[i+k] < in[j+k]) j = max(j+k+1, i+1); //此时从 i~i+k 为开始的字符串都会小于相应的 j~j+k 位置开始的字符串，所以一定不以 j~j+k 为起点
else i = max(i+k+1, j+1);
}i = min(i, j);
题：
注意：输入字符的范围为 #33~#256，需要开 unsigned char，char 的范围在为 -128 ~ +127
KMP
利用后缀函数线性求一个模板串在一个文本串里出现的次数或位置等等
预处理出模板串的最大相等前后缀，与文本串进行匹配的时候每次匹配不上就将模板串的调到与此时后缀相同的前缀位置
预处理代码
inline void prefix(string s, int pi[]){ // pi[i]表示 s 到第 i 个字符时的串的前后缀的长度
int len = s.length();
for(int i=1; i<len; i++){
int j = pi[i-1]; // j 表示到 i 前一个字符时的前缀最后一个字符的位置 + 1
while(j and s[i] != s[j]) j = pi[j-1]; //j 继续往前跳到前缀最后一个字符 + 1 的位置
if(s[i] == s[j]) ++j; //找到最大的 j 前后缀匹配上了，长度为位置 + 1
pi[i] = j;
}
}
code
#include<bits/stdc++.h>
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type int
#define qr(x) x=read()
typedef long long ll;
using namespace std;
inline Type read(){
char c=getchar(); Type x=0, f=1;
while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();
while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();
return x*f;
}
const int N = 1e6 + 5;
string s, t;
int n, m, pre[N];
inline void prefix(string s, int pi[]){
int len = s.length();
for(int i=1; i<len; i++){
int j = pi[i-1];
while(j and s[i] != s[j]) j = pi[j-1];
if(s[i] == s[j]) ++j;
pi[i] = j;
}
}
signed main(){ // a
// Aqrfre(a, a);
cin>>s>>t;
n = s.length(), m = t.length();
prefix(t, pre);
for(int i=0,j=0; i<n; i++){
while(j > 0 and s[i] != t[j]) j = pre[j-1];
if(s[i] == t[j]) ++j;
if(j == m){
cout<<i-m+2<<"\n";
j = pre[j-1];
}
}
for(int i=0; i<m; i++) cout<<pre[i]<<" ";
return 0;
}
AC 自动机
给定一个文本串和多个模式串，求出每个模式串在文本串中出现的次数，时间复杂度为所有模式串的长度和
为 trie 树 和 KMP 的思想结合
主要的三步：
-
trie 树正常建，不再叙述
-
构建 fail 指针：
fail 的实质含义： 如果一个点 \(i\) 的 fail 指针指向 \(j\)，那么 \(root\) 到 \(j\) 的字符串是 \(root\) 到 \(i\) 的字符串的可以在 trie 树中找到的最长的后缀。
在处理 \(i\) 节点时保证处理好了其父亲节点 \(fa\)，（所以使用 bfs），设 \(fa->i\) 的字符为 \(c\)，这时 \(fail_i\) 指向 \(fail_{fa}\ 'son_c\)。具体操作以及细节看链接中讲解
-
查询：
在 trie 树上跑文本串，每次到一个节点 \(i\)，不断向上跳 fail 指针到根节点，即为把【 $\forall j\in $ ( \(root\) 到 \(i\) 路径上的字符 ) 模板串 \(j\) -> \(i\) 】的贡献加上。
如最基础的求每个模式串是否在文本串中出现过：对于 trie 树上的每一个节点打个标记 \(tag\)，记以这个点结束的字符串的个数，查询的时候经过这个点一次就标记 \(tag=-1\)，保证每个点只走一次。如下文例题中的 【模板 1】
但如果我们要求的是每个模板串在文本串中出现了几次，显然就不能用上述的 -1 标记优化了，必须每次不断跳 fail 指针直到根节点，时间复杂度也明显不对了，所以考虑拓扑优化。
每次遇到一个节点不断跳 fail 指针会存在以下问题：
若有 fail 指针如下：9->7->4->2->1，并且我们跑文本串时走了 1-2-4-7-9 的路径，每次到一个节点都会再跳 fail 指针到 1 号点。而又容易发现 9 的贡献都会全加到 7 的贡献上，同样 7 的贡献都会全加到 4 的贡献上······所以我们每次遇到一个点，只更新该点的贡献，先不往回跳 fail，最后“从深到浅”处理完 9 的所有贡献，再去处理 7 的贡献，这样可以保证每个点只处理一次，复杂度是对的，本质上也就是一次拓扑的过程。
相当于把 fail 指针看成是一条单向边，且每个点的出度为 1，以拓扑图的方式从深到浅更新点对应的答案。
注意题目是否存在多个模板串长得一样，若有这种情况，还需要开个 map 记一下每种字符串在 trie 树上最后一个节点的编号
整个 trie 树函数代码：
gp_hash_table<string, int>ma; //pbds 哈希表
struct Trie{
int rt = 1, t[M][28], fail[M<<5], in[M<<5];
inline void insert(string s, int th){
int len = s.length(), u = 1;
for(int i=0; i<len; i++){
int v = s[i] - 'a';
if(!t[u][v]) t[u][v] = ++rt;
u = t[u][v];
}
ma[s] = u; // 记字符串 s 对应的节点
}
inline void getfail(){
for(int i=0; i<26; i++) t[0][i] = 1;
fail[1] = 0; q.push(1);
while(q.size()){
int u = q.front(); q.pop();
for(int i=0; i<26; i++){
int v = t[u][i];
if(!v){ t[u][i] = t[fail[u]][i]; continue; }
fail[v] = t[fail[u]][i];
in[fail[v]]++; q.push(v);
}
}
}
inline void update(string s){
int u = 1, len = s.length();
for(int i=0; i<len; i++){
int v = s[i] - 'a';
u = t[u][v]; cnt[u]++;
}
}
inline void topu(){
for(int i=1; i<=rt; i++)
if(!in[i]) q.push(i);
while(q.size()){
int u = q.front(); q.pop();
int v = fail[u];
cnt[v] += cnt[u]; in[v]--;
if(!in[v]) q.push(v);
}
}
}tri;
题
【模板 1】：求有多少个不同的模式串在文本串里出现过。
code
【模板】AC 自动机：求每个模板串在文本串中出现的次数。code
—— AC 自动机写于 11.8
