【填算符】（log 值域的做法）

比赛在这里呢

填算符

~~下发题解说的神马东西，赛时根本想不到~~

讲一个赛时想得到的 $O(n\log 值域)$ 的思路，很好理解

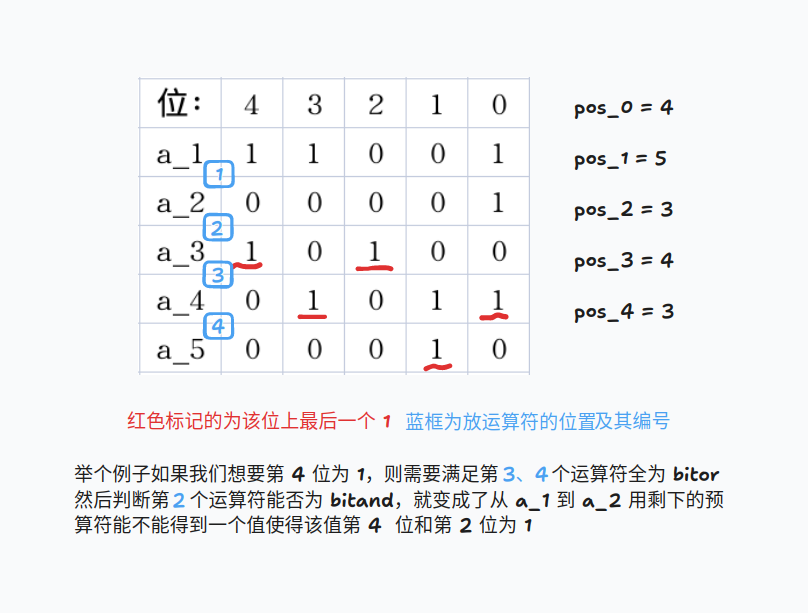
我们处理出二进制下每一位上的 1 的最后一次出现的位置，将第 $i\ (i\in[0,60])$ 位上的 1 最后一次出现的位置记作 $pos_i$

同时我们设 $H=n-k-1$ 为总共有的 bitor 的操作数

有以下结论：由于 $pos_i$ 是 $i$ 位上最后一个 1，所以一旦它后面放了一个与，这一位上就是 0 了；若我们想要这一位为 1，必须至少满足从 $pos_i$ 到最后的运算符全是 bitor。

发现有以下情况：

若 $n-pos_i>H$，即 $pos_i$ 之后需要放的运算符的数量比 bitor 的总操作数多，也就是说在 $pos_i$ 之后我一定需要放 bitand 操作，所以这种情况下这一位一定不对答案有贡献
若 $n-pos_i<H$，也就是说我可以从 $pos_i$ 的前一个位置开始到最后全放 bitor 操作，那么这样第 $i$ 位上可以是 1，为了使值最大，所以第 $i$ 位上一定要是 1，所以从第 $pos_i$ 位到最后必须全是 bitor 操作，对于这种情况的 $i$ 我们记为合法位
若 $n-pos_i=H$，也就是说从第 $pos_i$ 到最后的运算符可以全是 bitor 操作，但 $pos_i$ 的前一位只能是 bitand
所以我们特判从第 1 个位置到 $pos_i$ 的前一位全放 bitand 能不能让到第 $pos_i$ 个数时得到的值第 $\forall $ $j 满足 [pos_j=pos_i]$ 位为 1，若能则该位也为合法位，否则不合法

对于所有合法位的 $pos$ 取最小值设为 $end$，因为已经保证 $end$ 到最后的预算符全是 bitor，此时有一下两种可能，而我们想尽量构成第二种可能：

$end$ 的前一位预算符也为 bitor，这样我们一定能达到答案最大了，想使答案最优直接让从 $end-2$ 开始的 $k$ 个运算符为 bitor 就好了
$end$ 的前一位在某些情况为 bitand 也是可以使答案最大的，所以我们判断能不能让 $end$ 的前一位为 bitand 同样使答案最大；
发现可以的条件相当于从第 $end-1$ 个数到最前面用仅剩的 bitor 操作得到一个答案，使得这个答案第 $\forall $ $i 满足 [pos_i=end]$ 位为 1，若能满足条件则第 $end-1$ 个操作符为 bitand。

满足条件的判断又和上述的第三个情况判断一致了，相当于以 $end-1$ 为下界，再做一次求 $min(合法的\ pos)$，实质上是不断的递归。

形式化如下：

所以一个递归 $dfs(end, H)$ 表示下界为 $end$，还剩 $H$ 个 bitor 操作，判断能不能得到我想要的答案：

若不能则直接从第 $end-2$ 开始的 $k-res$ 个运算符全为 bitand 就是答案（$res$ 为在之前的递归中已经确定的 bitand 的个数）

若能则第 $end-1$ 个位置可以为 bitand，并设 $end'=min(这一层中合法的\ pos)$，继续递归 $dfs(end',H-(end-end'))$ 判断第 $end'-1$ 个位置能不能为 bitand。

code：

#include<bits/stdc++.h>
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type ll
#define qr(x) x=read()
typedef __int128 INT;
typedef long long ll;
using namespace std;

inline ll read(){
    char c=getchar(); ll x=0, f=1;
    while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();
    while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();
    return x*f;
}

const int N = 1e6 + 5; 
const int maxn = 1e8;

int n, k, K; ll a[N], b[N];

int la[62], pre[62][N], zh[62], X;
vector<int>v[N], ans, tem, num;

inline bool check(int pos, int op){ // 判断从第一个运算符到第 pos 个全为 & 能不能使得到的值满足条件
    int now = pos + 1; ll x = 0;
    for(int i : v[now]) x += (1 << i);
    if(~X) x += (1 << X);
    int y = a[1];
    for(int i=2; i<=now; i++)
        y = y & a[i];
    if(y & x == x) return true;
    return false;
}

inline void dfs(int pos, int H){ // 递归函数
    if(pos <= 0 and H <= 0) return;
    int now = pos + 1, end = 2e9;
    bool f = true; X = -1;
    for(int x : tem) v[pre[x][now]].clear(); //为方便更新新的一层的 V ，先清空
    for(int x : tem){
        if(pos - pre[x][now] > H or !pre[x][now]){
            f = false; break;
        }
        else if(pos - pre[x][now] < H) // 合法则更新 end 并加入 V
            end = min(end, pre[x][now] - 1), v[pre[x][now]].emplace_back(x);
        else{
            X = x;
            if(pre[x][now] == 1 or check(pre[x][now] - 1, 1))
                end = min(end, pre[x][now] - 1), v[pre[x][now]].emplace_back(x);
            else f = false;
        }
    }
    if(f) ans.emplace_back(pos), k--; // pos 位可以为 &，加到答案中
    if(!k) return;
    if(f and end >= k){
        tem.clear(); for(int x : v[end+1]) tem.emplace_back(x);
        dfs(end, H-(pos-end-1)); //继续递归判断 end 位可否为 &
    }
    else{
        int cnt = k; // pos 位不可以为 &，则最优方案为从 pos-1 到 pos-cnt 全为 &
        for(int i=pos-cnt; i<pos; i++)
            k--, cout<<i<<" ";
        return;
    }
}

signed main(){ // bitop
    Aqrfre(bitop, bitop);

    qr(n); qr(k); K = k;
    for(int i=1; i<=n; i++){
        qr(a[i]);
        for(int j=0; j<62; j++){
            if(a[i] & (1ll << j)) pre[j][i] = la[j], la[j] = i;
            else pre[j][i] = pre[j-ans.size()][i-1]; // 二进制下第 j 位为 1 在第 i 个数之前一次出现的位置
        }
    }

    if(k == n - 1){
        for(int i=1; i<=k; i++) cout<<i<<" ";
        return 0;
    }

    for(int j=0; j<62; j++) //  V 存当前这一层递归的下界包含的 最后一个 1 出现在这个下界的 二进制位
        if(la[j]) zh[j] = la[j], v[zh[j]].emplace_back(j);

    int H = n - 1 - k, endi = 1e9; bool go = false;
    for(int i=0; i<62; i++){ // 把第一次递归剖出来单独做
        if(!zh[i]) continue; 
        if(n - zh[i] > H) continue; 
        if(n - zh[i] < H){
            endi = min(endi, zh[i] - 1);
            continue;
        }
        if(go) continue;
        if(n - zh[i] == H){
            if(check(zh[i] - 1, 0)){ //特殊的：合法直接输出
                for(int i=1; i<=k; i++)
                    cout<<i<<" ";
                return 0;
            }
            go = true;
        }
    }

    for(int x : v[endi+1]) tem.emplace_back(x); //tem 暂存下界这个数的 V

    H -= (n - endi - 1);

    dfs(endi, H);
    sort(ans.begin(), ans.end());
    
    for(int x : ans) cout<<x<<" ";



    return 0;
}

posted @ 2024-11-04 09:46 Aqr_Rn 阅读(382) 评论(16) 编辑收藏举报

刷新页面返回顶部

Aqr's blog

【填算符】（log 值域的做法）

填算符

code：

公告