CSP 集训(9.23-9.26)
用来整理模拟赛等
9.23
csp-3【noip23 ZR二十连测 DAY10】
保龄.
A.奇观
狗市题目描述。

不是这题意太大歧义了吧,我讨厌的第二种出题人——题意描述相当不清。
CTH:13 座城市又不代表是 13 座不同的城市。
直接看形式化题目的话(如果能看懂要干什么)那这题确实不难。
解:
容易发现,答案就是 \(C\times C \times F\)。(\(C、F\) 分别表示组成一个 C、F 的方案数)
关键在于 \(CCF\) 怎么求?看懂题意的话,较容易明白:
记 \(v1_i =∑_j[(i, j) ∈ E] ,v2_i=∑_{j,k} [(i, j) ∈ E ∧ (j, k) ∈ E] = ∑_j[(i, j) ∈ E]v1_j\);
分别为以 \(i\) 为端点能拼成如下形式的方案数。
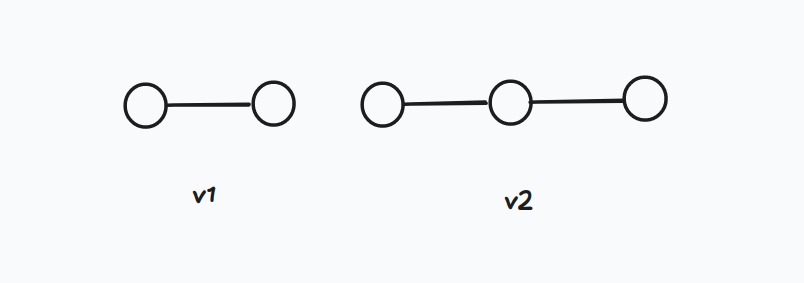
那么有 \(C=\sum_i v1_i\times v2_i\) , \(F = \sum v1_i \times \ v1_i \times v2_i\) 。
显然 \(v1_i\) 其实就等于删去 \(m\) 条边后的出度。现在考虑 \(v2_i\) 如何求。
我们再求一个 \(sum=\sum_i v1_i\),把每个 \(v2_i\) 都赋成 \(sum\),删去了哪些 \(i,j\) 相连的边,就减去 \(v1_j\) 即可。
B.铁路

随便钦定一个根跑 \(dfs\) 得到所有点的深度 \(dep\) 和父节点 \(fa\)
并查集维护连通块,每次把要合并的点都合并到其中深度最浅的点的并查集上,把 \(n+i\) 映射到这个最浅点上就好了。
C.光纤
9.24 补 从下午 14:00 调到 21:00,救命啊!
需要知识:凸包 向量叉积 旋转卡壳
- 构建一个包含所有点的凸包。
丁真的引理:答案直线就是平行于凸包所有边的直线中最优的那个。
显然:对于凸包的一条边,凸包上的点到该边的距离中最大的那个的一半就是该边对答案的贡献。
如下图中蓝边对于答案的贡献就是红色虚线(最远点到该边距离)的一半。
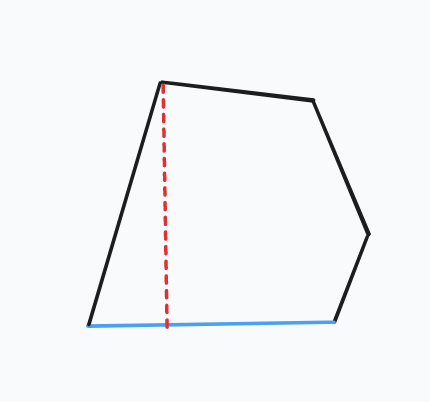
- 旋转卡壳 \(O(n)\) 找凸包上的每一条边的最远点,叉积计算最远点的距离,计算答案。
code
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 1e6 + 10;
int n, m, top, H;
pair<__int128, __int128>ans;
struct point{
__int128 x, y;
bool operator < (const point &A)const{
return x == A.x ? y < A.y : x < A.x;
}
}a[N], s[N], q[N];
char anss[N];
inline void print(__int128 x){
if(!x)putchar('0');
else{
if(x<0)x=-x,putchar('-');
int cnt=0;
while(x)anss[++cnt]=x%10+'0',x/=10;
for(int i=cnt;i;--i)
putchar(anss[i]);
}
}
point operator - (point A, point B){return {A.x - B.x, A.y - B.y};}
inline double Cross(point A, point B){return (double)(B.y - A.y) / (B.x - A.x);} //算直线斜率
inline void Andrew(){ //Andrew 算法建凸包
for(int i=1; i<=n; i++){
while(top > 1 and Cross(s[top], a[i]) <= Cross(s[top-1], s[top])) top--;
s[++top] = a[i];
}
int k = 0;
for(int i=n; i>=1; i--){
while(k > 1 and Cross(a[i], q[k]) <= Cross(q[k], q[k-1])) k--;
q[++k] = a[i];
}
for(int i=2; i<k; i++) s[++top] = q[i];
s[++top] = s[1]; // s[] 中存凸包上的每个点
}
inline __int128 Pf(__int128 x){return x * x;}
inline __int128 dis(point a, point b){return Pf(a.x - b.x) + Pf(a.y - b.y);}
inline __int128 _abs(__int128 x) {return x > 0 ? x : -1 * x;}
inline __int128 GetSum(point a, point b, point c){ //已知 a,b,c 三点,叉积求三点围成的三角形面积的两倍
return _abs((b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y));
}
inline void GetHigh(){
int j = 3; //旋转卡壳计算答案
for(int i=1; i<top; i++){
while(GetSum(s[i], s[i+1], s[j]) <= GetSum(s[i], s[i+1], s[j+1==top ? 1:j+1]))
j = (j + 1 == top ? 1 : j + 1);
if(!ans.second or 1.0 * ans.first / ans.second > 1.0 * Pf(GetSum(s[i], s[i+1], s[j])) / dis(s[i], s[i+1]))
ans.first = Pf(GetSum(s[i], s[i+1], s[j])), ans.second = dis(s[i], s[i+1]); //first,second 分别为答案的分子分母
}
}
int main(){
freopen("a.in", "r", stdin), freopen("a.out", "w", stdout);
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin>>n;
if(n == 2){
cout<<"0/1\n"; return 0;
}
for(int i=1; i<=n; i++){
int x, y; cin>>x>>y;
a[i].x = x, a[i].y = y;
}sort(a+1, a+1+n);
n = unique(a+1, a+1+n, [](const point &A, const point &B){return A.x==B.x&&A.y == B.y;}) - (a+1);
Andrew();
GetHigh();
__int128 gcd = __gcd(ans.first, ans.second*4); //因为面积算的是三角形的两倍,平方后就是四倍,分母乘以 4
print(ans.first/gcd); putchar('/'); print(ans.second*4/gcd);
return 0;
}
CSP-4
9.25 由上文可知,改了一下午和一晚上的凸包( 先咕网络流和超级分讨了!
A.商品
9.26 早读偷偷打的。。。本来在被 \(**\) 下发题解折磨, 5k 讲了一个很简单也很快的解法,绝!
首先显然区间长度为 \(d\) 时才能最优, \(l\) 确定时,\(r\) 则为 \(l+d\)。
这个题是想让我们求不同的 \([l,r]\) 区间中所有两两相邻数的差,\(\sum _{i=1} ^{n}|a_i-a_{i+1}|\) ,也就是 \(\sum a_i和a_{i+1}中大减小\),可以转化为 \(\sum 大 - \sum 小\)。那么我们把所有 \(a_i 和 a_{i+1}\) 中大的存到一个数组 \(b\) 里,小的存到一个数组 \(c\) 里,分别排序。
还有一个显然的结论:区间一端固定在一个原序列的元素上时较优,这是 \(60pts\) 暴力需要的结论。
那么 \(l\) 和 \(r\) 最多只有 \(2\times n\) 种情况,所以 \(O(n)\) 枚举当前哪一个元素作为区间的一端,对于每一组区间 \([l,r]\),用二分找区间外的元素,前缀和维护区间内的元素,大总和减小总和就是当前区间的答案,所有区间的答案取 min 即可。
B.价值
发现多写几层循环的话不用那么多分讨了,设 \(f_{i,0/1,0/1,0/1}\) 表示 \(i\) 这个点是否匹配上,以该点为根的子树中最左边的叶子结点是否向左匹配,最右边的叶子结点是否向右匹配 的状态下的方案数。
注:点是否匹配指该点的连边是否选进一个边集里。
设计状态转移就行,有些细节但不难设计。
C.货币
9.26 花了一上午学了网络流,发现算法没搞的很明白,但在 lxyt 的细心教导下,把建模搞清楚了。
写了 题解
多校-1
DP 专场,只拿了 T1 60pts 暴力。

A.几何
发现我能看着官方题解打出这个题挺不容易的,其实可能赛后看下发题解改题比赛时 AC 还难吧。
设 \(f_{i,j,k}\) 表示 \(s\) 的 \([1,i]\) 位可以由 (\(x\) 重复加上 \(x_{[1,j]}\))$ + $ (\(y\) 重复加上 \(y_{[1,k]}\) )构成。转移如下:

发现炸时空,考虑用位运算优化,bitset 存 \(f_{i,j}\) 表示 \(i,j\) 下的所有 \(k\) 的状态,转移代码如下:
(我又滚掉一维,仅仅是方便自己写 memset 而不用写循环清空数组)
memset(f, 0, sizeof f);
f[0][0] = 1;
for(int i=0; i<n; i++){
int now = i & 1, to = (i + 1) & 1;
for(int j=0; j<=len1; j++){
if(s[i+1] == c[0][j%len1+1]) f[to][j%len1+1] = f[to][j%len1+1] | f[now][j];
for(int k=0; k<=len2; k++)
if(f[now][j][k] & 1 and s[i+1] == c[1][k%len2+1])
f[to][j][k%len2+1] = f[to][j][k%len2+1] | 1;
}
for(int j=0; j<=len1; j++) f[now][j].reset();
}
B.分析
又是树形 DP。

设 \(f_{i,0/1,0/1}\) 表示(当前点为 \(i\) 时,该点出度的奇偶性,以该点为根的子树中是否有出度为奇数的点) 状态下的答案。
设计状态跑树形 dp 转移就可以了。
[C.]
咕咕咕,下一道题就该这个!


