「模拟赛」暑期集训CSP提高模拟3（7.20）
仍在施工...
$165 pts, Rank 18$
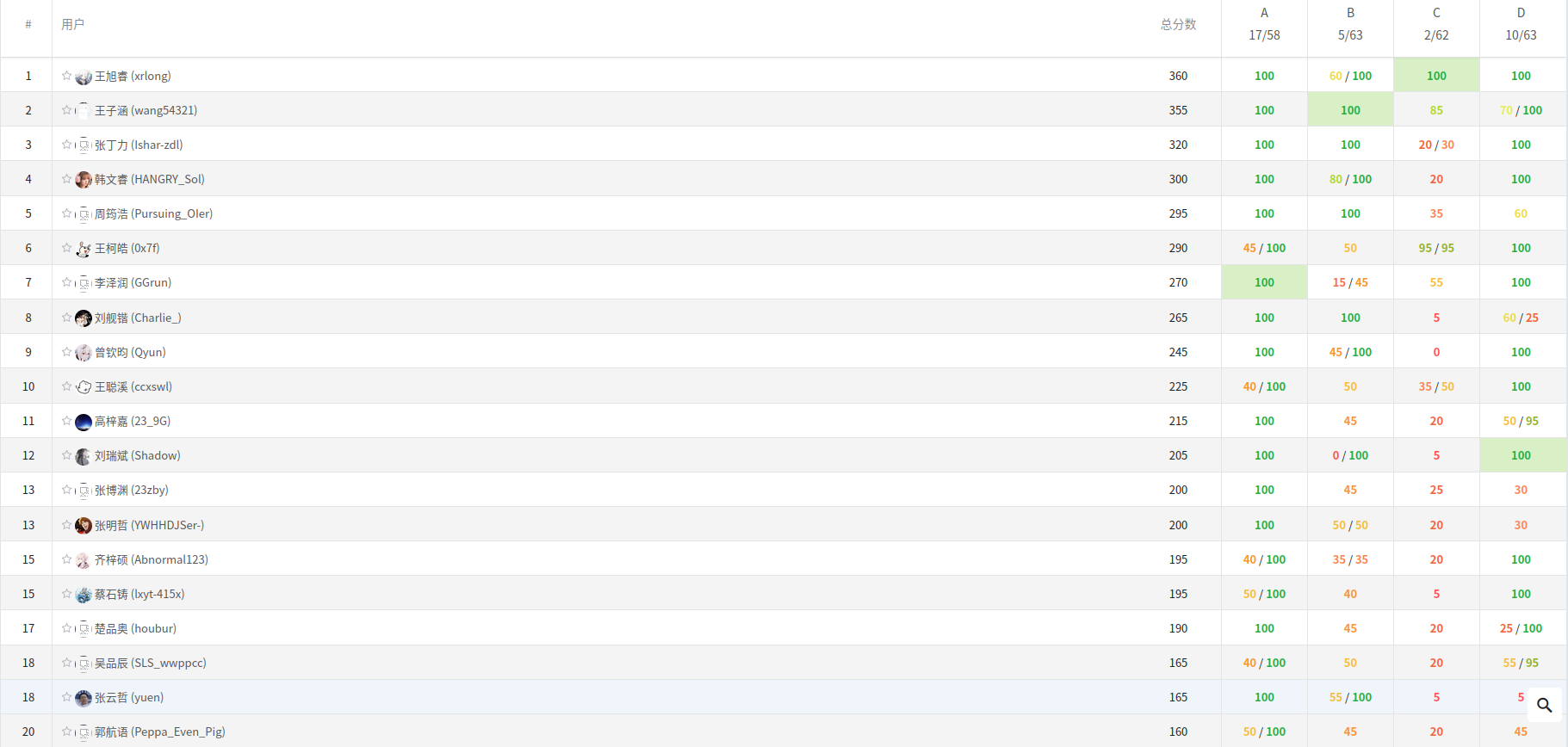
B 题挂了 45 分，不然可以 AC 两道题的，呜
题目列表：
A.abc猜想
题意：
给定三个正整数 \(a,b,c\)，你需要求出 \(a^b\) 除以 \(c\) 并向下取整得到的值对 \(c\) 取模的结果。
赛时分析：
大概十天之前 和 \(DrRatio\)、\(GGrun\) 玩洛谷随机跳题做过一道类似且难度大于等于这个的题，开赛没十秒， GGrun：做过做过这个，于是十分钟切了。
正解:
求 \(a^b\) 显然快速幂，模什么呢，模 \(c\) 的话之后再 \(\div c\) 结果显然为 0，所以我们模 \(c^2\)。
code:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll a, b, c;
ll qpow(ll x, ll y, ll mod){
ll ans = 1;
while(y)
{
if(y & 1) ans = ans * x % mod;
x = x * x % mod;
y >>= 1;
}
return ans;
}
signed main(){
// freopen("in.in", "r", stdin); freopen("out.out", "w", stdout);
scanf("%lld%lld%lld", &a, &b, &c);
ll ans = qpow(a, b, c * c) / c;
ans = ans % c;
printf("%lld", ans);
return 0;
}
B.简单的排列最优化题
题意：
对长度为 \(n\) 的排列 \(π=(π1,π2,…,πn)\)，定义它的权值 \(wt(π)=∑_{i=1}^n∣π_i−i∣\)，定义它的 k-移位为新的排列 \(πk=(πn−k+1,πn−k+2,…,πn,π1,…,πn−k)\)。特别的，\(π_0=π\)。
现在给定长度为 \(n\) 的排列 \(π\)，请找到一个 \(k∈[0,n−1]\)，使得 \(wt(πk)\) 最小。
赛时分析：
上来想半天没想到什么正解，于是决定先打上暴力 \(O(n^2)\)， 还写了个循环，发现每次状态完全可以由上次转移而来，不需要每次都 \(O(n)\) 计算，于是想如何转移，细节很多，打了一个多小时过了所有样例，但数组开小了加之有个地方的 \(=\) 忘了写，挂了\(45pts\)。
正解：
枚举移位的位数 \(k\)，预处理初始的总和 \(sum\)，以及小于 0 的个数 \(sm\) 和大于等于 0 的个数 \(bi\)，对于每一个 \(k\)，\(sum\) 都可以由 \(lastsum+sm-bi\) 加上特判最后一位数转移，考虑转移 \(sm,bi\) 即可。
code：
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 4e6 + 10;
int n, a[N];
int sm_0, bi_0, b_s[N];
ll sum;
signed main(){
// freopen("in.in", "r", stdin); freopen("out.out", "w", stdout);
scanf("%d", &n);
for(int i=1; i<=n; i++){
scanf("%d", &a[i]);
sum += (long long)abs(a[i] - i);
if(a[i] - i < 0) sm_0++;
else{
bi_0++;
if(a[i] != n) b_s[a[i]-i]++;
}
}
int ansid = 0; ll ans = sum;
for(int k=1; k<n; k++){
if(a[n-k+1] >= n) bi_0--;
if(a[n-k+1] < n) sm_0--;
bi_0 -= b_s[k-1]; sm_0 += b_s[k-1];
sum = sum + sm_0 - bi_0 + abs(a[n-k+1] - 1) - abs(a[n-k+1] - n);
if(a[n-k+1] != n) b_s[a[n-k+1]-1+k]++;
if(a[n-k+1] < 1) sm_0++;
if(a[n-k+1] >= 1) bi_0++;
if(sum < ans){
ans = sum, ansid = k;
}
}
printf("%d %lld", ansid, ans);
return 0;
}
C.简单的线性做法题
D.简单的线段树题
正解：
雀氏线段树，我们发现对于每一棵树，最多开平方到 1 以后便一直为 1，我们在只需维护一个区间总和，当区间总和等于区间大小时，那么该区间内所有数都为 1，不再需要递归更新，直接返回即可。
code：
#include<bits/stdc++.h>
#define int long long
#define ll long long
using namespace std;
const int N = 4e6 + 10, N1 = 1e6 + 10;
int n, m;
ll a[N1];
namespace Segment_tree
{
#define lson rt<<1
#define rson rt<<1|1
ll sum[N];
void pushup(int rt){
sum[rt] = sum[lson] + sum[rson];
}
void build(int rt, int l, int r){
if(l == r){
sum[rt] = a[l];
return;
}
int mid = l + r >> 1;
build(lson, l, mid);
build(rson, mid+1, r);
pushup(rt);
}
void update(int rt, int l, int r, int ql, int qr){
if(l == r){
sum[rt] = sqrt(sum[rt]);
return;
}
if(sum[rt] == r - l + 1) return;
int mid = l + r >> 1;
if(ql <= mid) update(lson, l, mid, ql, qr);
if(qr > mid) update(rson, mid+1, r, ql, qr);
pushup(rt);
}
ll find(int rt, int l, int r, int ql, int qr){
if(ql <= l and r <= qr){
return sum[rt];
}
int mid = l + r >> 1; ll ans = 0;
if(ql <= mid) ans += find(lson, l, mid, ql, qr);
if(qr > mid) ans += find(rson, mid+1, r, ql, qr);
return ans;
}
}
signed main(){
// freopen("in.in", "r", stdin); freopen("out.out", "w", stdout);
scanf("%lld", &n);
for(int i=1; i<=n; i++){
scanf("%lld", &a[i]);
}
Segment_tree::build(1, 1, n);
scanf("%lld", &m);
for(int i=1; i<=m; i++){
int op, l, r;
scanf("%lld%lld%lld", &op, &l, &r);
if(op == 1){
printf("%lld\n", Segment_tree::find(1, 1, n, l, r));
}
else{
Segment_tree::update(1, 1, n, l, r);
}
}
return 0;
}
