背包dp

一. 背包DP

1. 0/1背包:

要素：

• 每个物品只有选一次或不选两种选择
• n个物品 ，每个物品只有一件，第i个物品体积为vi，价格pi,现在有一个体积为V的背包，选出若干件物品使背包里价值最大
• 装入第i件物品已用体积为j时，有两种选择：
  1.不放入第i件物品：f[i][j]=f[i-1][j]
  2. 放入第i件物品：f[i][j]=f[i-1][j-v[i]]+c[i]

状态转移方程： f[j] = max(f[j], f[j-v[i]] + w[i]);

代码模板如下：

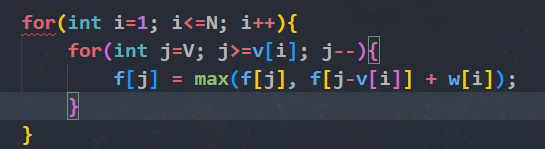
例：

输入样例

 4 5
 1 2
 2 4
 3 4
 4 5

输出样例

 8

代码如下：

#include<bits/stdc++.h>
using namespace std;

const int MAX = 1050;

int N, V, v[MAX], w[MAX];
int f[MAX];

int main(){

    scanf("%d%d",&N, &V);
    for(int i=1; i<=N; i++){
        scanf("%d%d",&v[i], &w[i]); 
    }

    for(int i=1; i<=N; i++){
        for(int j=V; j>=v[i]; j--){
            f[j] = max(f[j], f[j-v[i]] + w[i]); //f[j]表示体积为j时的价值
        }
    }
    printf("%d", f[V]);

    return 0;
}

2. 完全背包:

- 每个物品可以选择无数次

• 有n件物品，每个物品无数件，第i个物品体积为vi，价格为ci现在有一个体积为V的背包，请你从n件物品里选出若干件放进背包里使得背包里的物品价值最大。

• 我们用和0/1背包一样的状态，f[i][j]表示前i种物品放入一个容量为j的背包的最大价值，那我们应该用k表示当前容量下可以装第i种物品的件数，那么k的范围应该是0≤k≤V/v[i].
• 状态转移方程为： f[i][j]=max(f[i-1][j],f[i-1][j-kv[i]]+kc[i])
• 极端情况比如n个物品体积均为1，此时k=V，时间效率为O(n*V2)
  
  

模板代码：

• 因为每种物品有无穷个，体积也是无穷的，则我们可以省略一维。推理如下：

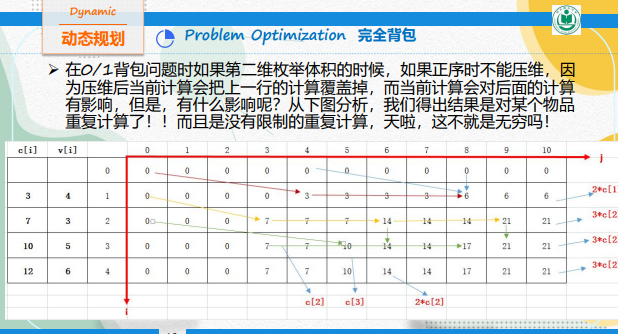
• 则最终化简后：

状态转移方程：f[j] = max(f[j], f[j-v[i]] + w[i]);

模板如下：

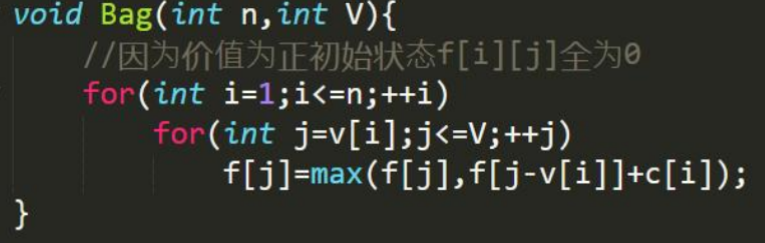
太神奇了，第二维倒序是0/1背包，正序是完全背包，我就问你们服不服！

3. 多重背包:

• 有n种物品，每种物品bi件，第i个物品体积为vi，价格为ci.现在有一个体积为V的背包，请你从n件物品里选出若干件放进背包里使得背包里的物品价值最大。(每种物品可以选固定次数)
• 数据范围：0<n<=100,0<V<=10000.物品和背包体积为正整数，保证所有物品价值为正，且价值和在int范围内
• 这题目和完全背包问题很类似。基本的方程只需将完全背包问题的方程略微一改即可，因为对于第i种物品有b[i]+1种策略：取0件，取1件…取b[i]件。令f[i][j]表示前i种物品放入一个容量为j的背包的最大权值，则有状态转移方程：f[i][j]=max(f[i-1][j-kv[i]]+kc[i]) 0<=k<=b[i]
• 复杂度是O(V*Σb[i])。 显然时间效率有点低下，我们可以借鉴完全背包的二进制优化。
  
  
  
  
  
  

例：

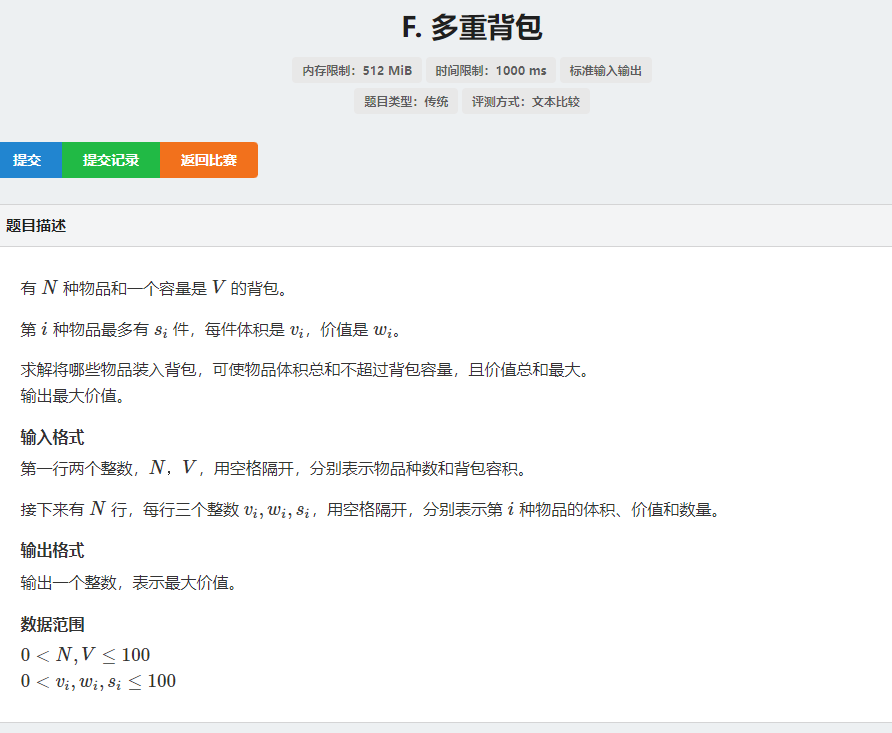
样例输入：

 4 5
 1 2 3
 2 4 1
 3 4 3
 4 5 2

样例输出：

10

解：

#include<bits/stdc++.h>
using namespace std;

const int MAX = 10050;

int n, m;
int v[MAX], w[MAX], s[MAX];
int f[MAX];

int main(){

    scanf("%d%d",&n, &m);
    for(int i=1; i<=n; i++){
        scanf("%d%d%d",&v[i], &w[i], &s[i]);
    }

    for(int i=1; i<=n; i++){
        for(int j=1; j<=s[i]; j++){  //j遍历i物品使用次数
            for(int k=m; k>=v[i]; k--){
                f[k] = max(f[k], f[k-v[i]]+w[i]); //如0/1背包一样
            }
        }
    }
    
    printf("%d", f[m]);

    return 0;
}

4. 分组背包:

• 每若干物品分为一组，每组中只能选一件物品。
• 现有体积为V的背包，有n种物品，第i件物品重量为wi，价值为pi。这些物品被划分为若干组，每组中的物品互相冲突，最多选一件。
• 每组物品要么一件不取，要么只取其中的一件，跟0/1背包很类似，0/1背包是对单个物品而言，而分组背包是对分组而言
• 定义f[i][j]表示第i组物品在背包容量为j对第i组的第k个物品进行决策的最大价值，动态转移方程为: f[i][j]=max(f[i-1][j],f[i-1][j-w[g[i][k]]]+c[g[i][k]]

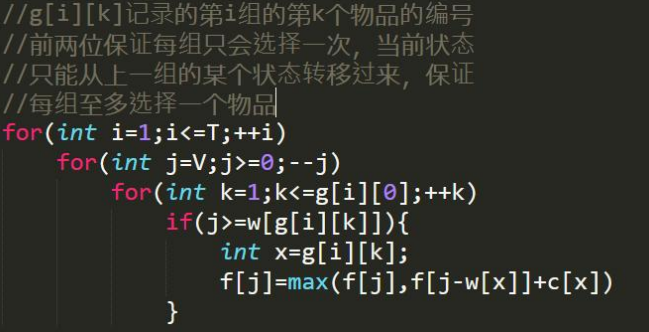
例：

样例输入：

 10 6 3
 2 1 1
 3 3 1
 4 8 2
 6 9 2
 2 8 3
 3 9 3

样例输出：

20

解：

#include<bits/stdc++.h>
using namespace std;

const int MAX = 1500;

int n, V, T;
int m[MAX], p[MAX], vp[MAX][MAX], g[MAX];	 
int f[MAX];
int main(){	

    int P;
    scanf("%d%d%d",&V, &n, &T);
    for(int i=1; i<=n; i++){
        scanf("%d%d%d",&m[i], &p[i], &P);
        g[P]++;  //g[P]表示P组中物品数量
        vp[P][g[P]] = i;  //eg.vp[1][2]表示第一组中第二个物品
    }

    for(int i=1; i<=10; i++){  //第一层按组依次遍历
        for(int j=V; j>=0; j--){
            for(int k=1; k<=g[i]; k++){  //该组中物品一次遍历求最大
                if(j >= m[vp[i][k]])
                    f[j] = max(f[j], f[ j-m[vp[i][k]] ]+p[vp[i][k]] );
            }
        }
    }
    printf("%d", f[V]);

return 0;
}