作业

这个网页可以更新东西，凑合用吧

1、第6题

1.1 python源代码

# -*- coding:utf-8 -*-
# @Time    : 2018/9/6 10:48
# @Author  : yuanjing liu
# @Email   : lauyuanjing@163.com
# @File    : question_6.py
# @Software: PyCharm

import math

# 计算级数不同方法求和的精度
# 参数要求n必须为大于1的正整数
def series_sum(n):
    # 第一种方法：按正常次序相加
    Sn1, Sn2, Sn3, Sn4 = 0, 0, 0, 0
    for i in range(1, n+1):
        Sn1 = Sn1 + ((-1)**(i+1))*(1/i)
    # 第二种方法：按相反次序相加
    for j in range(n, 0, -1):
        Sn2 += ((-1)**(j+1))*(1/j)
    # 第三种方法：按成对组合数相加
    k = 1
    while k <= n:
        tmp3 = ((-1)**(k+1))*(1/k) + ((-1)**(k+2))*(1/(k+1))
        Sn3 += tmp3
        k = k + 2
    # 第四种方法：按成对组合的通分后结果相加
    l = 1
    while l <= n:
        Sn4 += 1/(l * (l+1))
        l += 2

    bz = math.log(2, math.e)
    result = {'Sn1': Sn1, 'Sn2': Sn2, 'Sn3': Sn3, 'Sn4': Sn4}
    # 是求绝对值
    result_jingdu = {'Sn1': abs(bz-Sn1), 'Sn2': abs(bz-Sn2), 'Sn3': abs(bz-Sn3), 'Sn4': abs(bz-Sn4)}
    result_sort = sorted(result_jingdu.items(), key=lambda e: e[1])

    print('第一种方法：按正常次序相加Sn1: %.16f' % Sn1)
    print('第二种方法：按相反次序相加Sn2: %.16f' % Sn2)
    print('第三种方法：按成对组合数相加Sn3: %.16f' % Sn3)
    print('第四种方法：按成对组合的通分后结果相加Sn4: %.16f' % Sn4)
    print('精度排序：%s > %s > %s > %s' %
          (result_sort[0][0], result_sort[1][0], result_sort[2][0], result_sort[3][0]))
    return result, result_jingdu, result_sort


# 测试
result0, result_jingdu0, result_sort0 = series_sum(10**6)

 

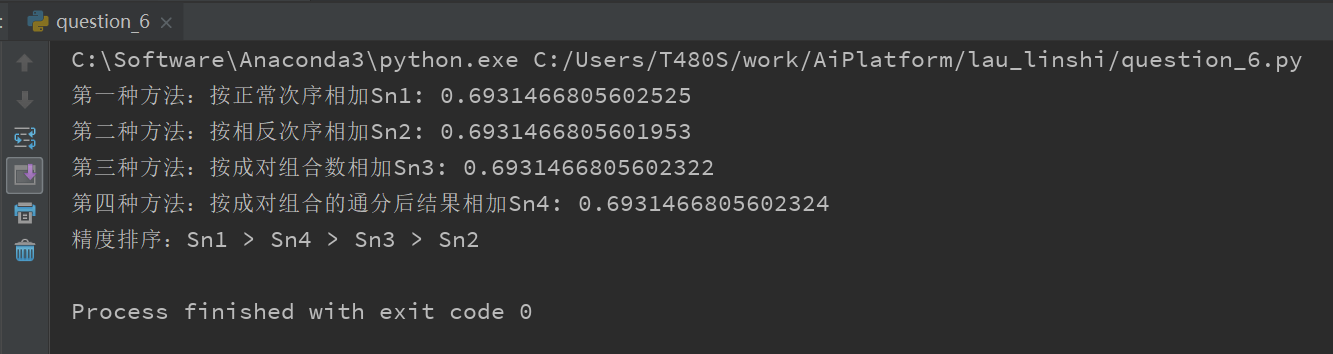
1.2 输出结果

第一种方法：按正常次序相加Sn1: 0.6931466805602525
第二种方法：按相反次序相加Sn2: 0.6931466805601953
第三种方法：按成对组合数相加Sn3: 0.6931466805602322
第四种方法：按成对组合的通分后结果相加Sn4: 0.6931466805602324
精度排序：Sn1 > Sn4 > Sn3 > Sn2

 

 

2、第2题

2.1 python源代码

# -*- coding:utf-8 -*-
# @Time    : 2018/9/5 22:42
# @Author  : yuanjing liu
# @Email   : lauyuanjing@163.com
# @File    : question_2.py
# @Software: PyCharm


# 此函数计算向量x长度为s的滑动和
def vector_sum(x, s):
    n = len(x)
    vector_sum = []
    if s <= n:
        i = 0
        while i <= n-s:
            tmp = 0
            for j in range(i, s+i):
                tmp += x[j]
            vector_sum.append(tmp)
            i += 1
        print('向量x长度为%d的滑动和: ' % s)
        print(vector_sum)
    else:
        print('错误：s必须小于等于n')
    return vector_sum


# 测试
x1 = [1, 2, 3, 4, 5, 6, 7, 8]
sum1 = vector_sum(x1, 3)
sum2 = vector_sum(x1, 4)
sum3 = vector_sum(x1, 5)
# sum2 = vector_sum(x1, 15)  # 会返回错误，s>n

 

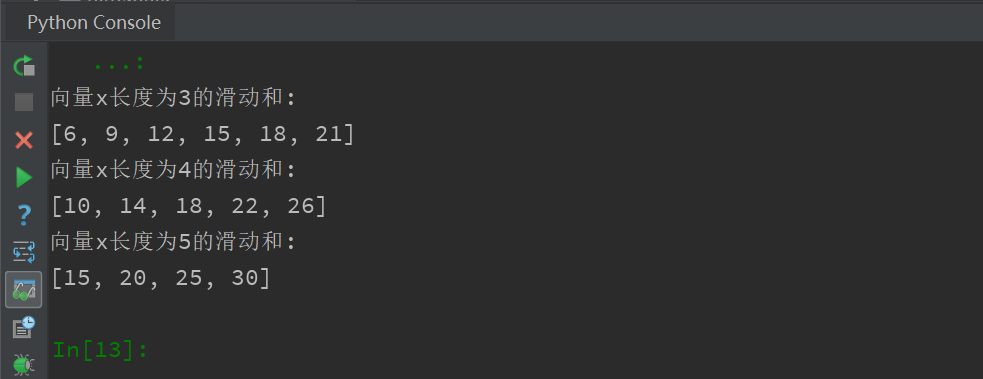
2.2 输出结果