时间序列算法理论及python实现（2-python实现）
如果你在寻找时间序列是什么？如何实现时间序列？那么请看这篇博客，将以通俗易懂的语言，全面的阐述时间序列及其python实现。
时间序列算法理论详见我的另一篇博客：时间序列算法理论及python实现 - 知-青 - 博客园
5 Python实现ARIMA模型
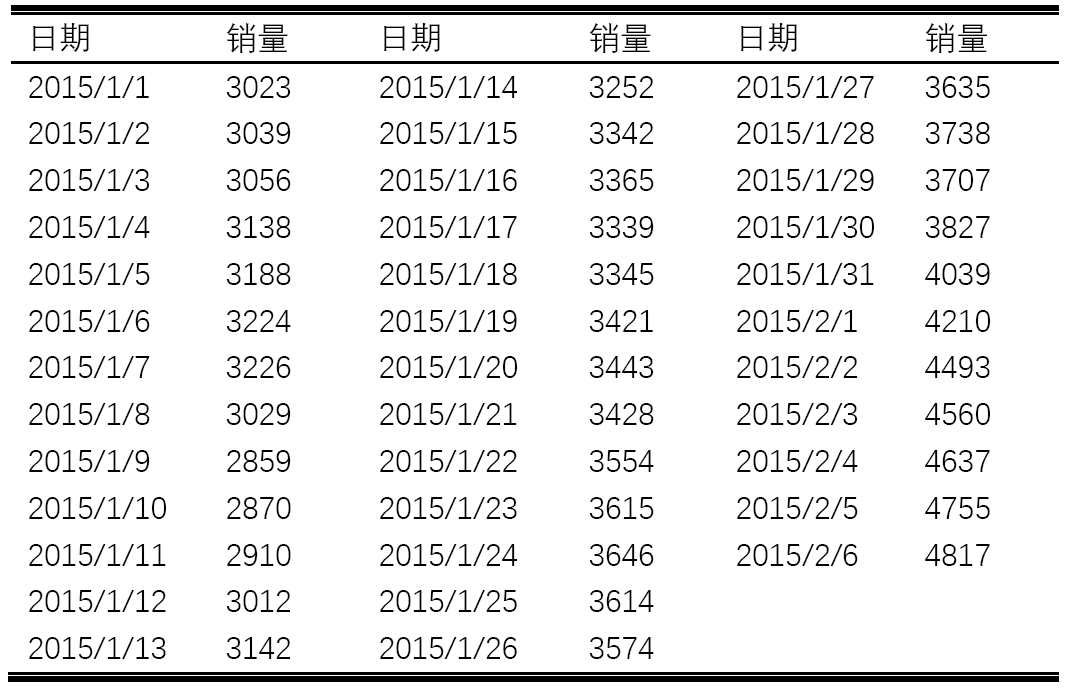
下面应用以上理论知识，对表6中2015/1/1~2015/2/6某餐厅的销售数据进行建模。
就餐饮企业而言，经常会碰到如下问题。
由于餐饮行业是胜场和销售同时进行的，因此销售预测对于餐饮企业十分必要。如何基于菜品历史销售数据，做好餐销售预测，以便减少菜品脱销现象和避免因备料不足而造成的生产延误，从而减少菜品生产等待时间，提供给客户更优质的服务，同事可以减少安全库存量，做到生产准时制，降低物流成本
餐饮销售预测可以看作是基于时间序列的短期数据预测，预测对象为具体菜品销售量
表6 原序列数据
5.1 环境配置
1 import pandas as pd 2 import matplotlib.pyplot as plt 3 from matplotlib.pylab import style 4 from statsmodels.tsa.stattools import adfuller as ADF 5 from statsmodels.stats.diagnostic import acorr_ljungbox # 白噪声检验 6 from statsmodels.tsa.arima_model import ARIMA 7 import statsmodels.tsa.api as smt 8 import seaborn as sns 9 style.use('ggplot') 10 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 11 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
要安装的环境有点小多，需要提前安装好。
5.2 导入数据
1 # 参数初始化 2 discfile = './data/arima_data.xls' 3 forecastnum = 5 4 5 # 读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式 6 data = pd.read_excel(discfile, index_col=u'日期')
代码和数据将会公布在Github，请到文末链接。
5.3 检验序列的*稳性
1 # 时序图 2 import matplotlib.pyplot as plt 3 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 4 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 5 data.plot() 6 plt.show() 7 8 # 自相关图 9 from statsmodels.graphics.tsaplots import plot_acf 10 plot_acf(data).show() 11 12 # *稳性检测 13 from statsmodels.tsa.stattools import adfuller as ADF 14 print(u'原始序列的ADF检验结果为：', ADF(data[u'销量'])) 15 # 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
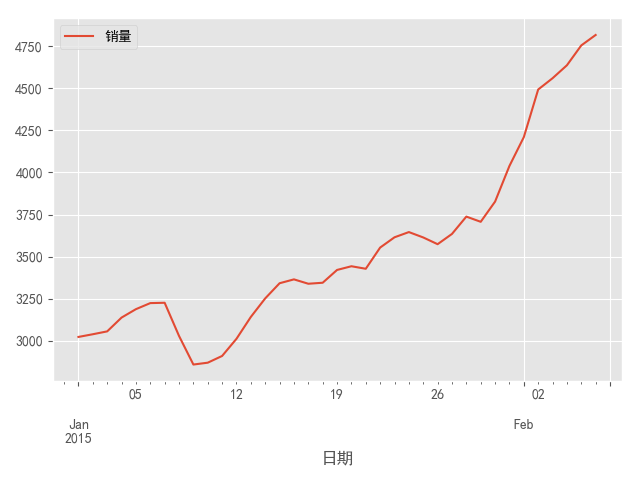
图3 原始序列的时序图
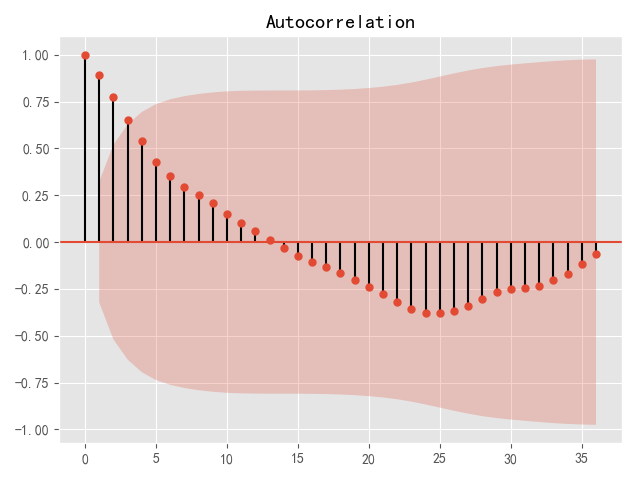
图4 原始序列的自相关图
原始时间序列的单位根检验
表7 原始序列的单位根检验
图3时序图显示该序列具有明显的单调递增趋势，可以判断为是非*稳序列；图4的自相关图显示自相关系数长期大于零，说明序列间具有很强的长期相关性；表7单位根检验统计量对应的P值显著大于0.05，最终将该序列判断为非*稳序列（非*稳序列一定不是白噪声序列）。
5.4 对原始序列进行一阶差分，并进行*稳性和白噪声检验
5.4.1 对一阶差分后的序列再次做*稳性判断
1 # 差分后的结果 2 D_data = data.diff().dropna() 3 D_data.columns = [u'销量差分'] 4 D_data.plot() # 时序图 5 plt.show() 6 plot_acf(D_data).show() # 自相关图 7 from statsmodels.graphics.tsaplots import plot_pacf 8 plot_pacf(D_data).show() # 偏自相关图 9 print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分'])) # *稳性检测
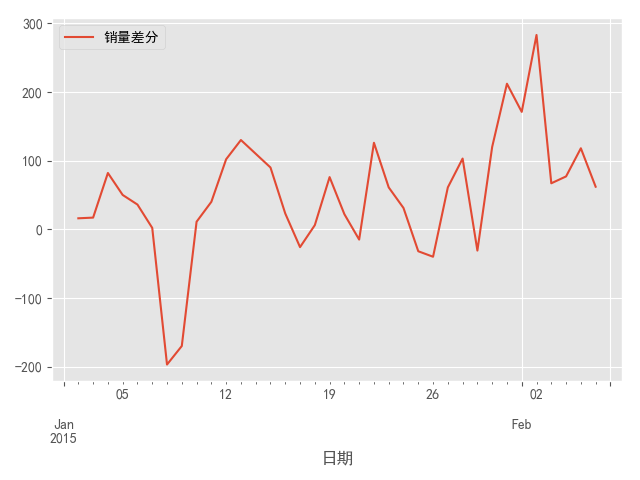
图5 一阶差分之后序列的时序图
图6 一阶差分之后序列的自相关图
一阶差分之后序列的单位根检验
表8 一阶差分之后序列的单位根检验
结果显示，一阶差分之后的序列的时序图在均值附*比较*稳的波动、自相关图有很强的短期相关性、单位根检验P值小于0.05，所以一阶差分之后的序列是*稳序列。
5.4.2 对一阶差分后的序列做白噪声检验（结果见表5-28）
from statsmodels.stats.diagnostic import acorr_ljungbox print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) # 返回统计量和p值
表9 一阶差分后的序列的白噪声检验
输出的P值远远小于0.05，所以一阶差分之后的序列是*稳非白噪声序列。
5.5 对一阶差分之后的*稳非白噪声序列拟合ARMA模型
下面进行模型定阶，模型定阶就是确定p和q。
5.5.1 人为识别实现模型定阶
一阶差分后自相关图（见图6）显示出1阶截尾，偏自相关图显示出拖尾性，所以可以考虑用MA(1)模型拟合1阶差分后的序列，即对原始序列建立ARIMA(0,1,1)模型。
图7 一阶差分后序列的偏自相关图
5.5.2 相对最优模型识别
计算ARMA(p,q)。当p和q均小于等于3的所有组合的BIC信息量，取其中BIC信息量达到最小的模型阶数。
1 from statsmodels.tsa.arima_model import ARIMA 2 3 data[u'销量'] = data[u'销量'].astype(float) 4 # 定阶 5 pmax = int(len(D_data) / 10) # 一般阶数不超过length/10 6 qmax = int(len(D_data) / 10) # 一般阶数不超过length/10 7 bic_matrix = [] # bic矩阵 8 for p in range(pmax + 1): 9 tmp = [] 10 for q in range(qmax + 1): 11 try: # 存在部分报错，所以用try来跳过报错。 12 tmp.append(ARIMA(data, (p, 1, q)).fit().bic) 13 except: 14 tmp.append(None) 15 bic_matrix.append(tmp) 16 17 bic_matrix = pd.DataFrame(bic_matrix) # 从中可以找出最小值 18 19 p, q = bic_matrix.stack().idxmin() # 先用stack展*，然后用idxmin找出最小值位置。 20 print(u'BIC最小的p值和q值为：%s、%s' % (p, q))
计算完成BIC矩阵如下（绘制程序在主程序，以上程序仅仅只有计算）
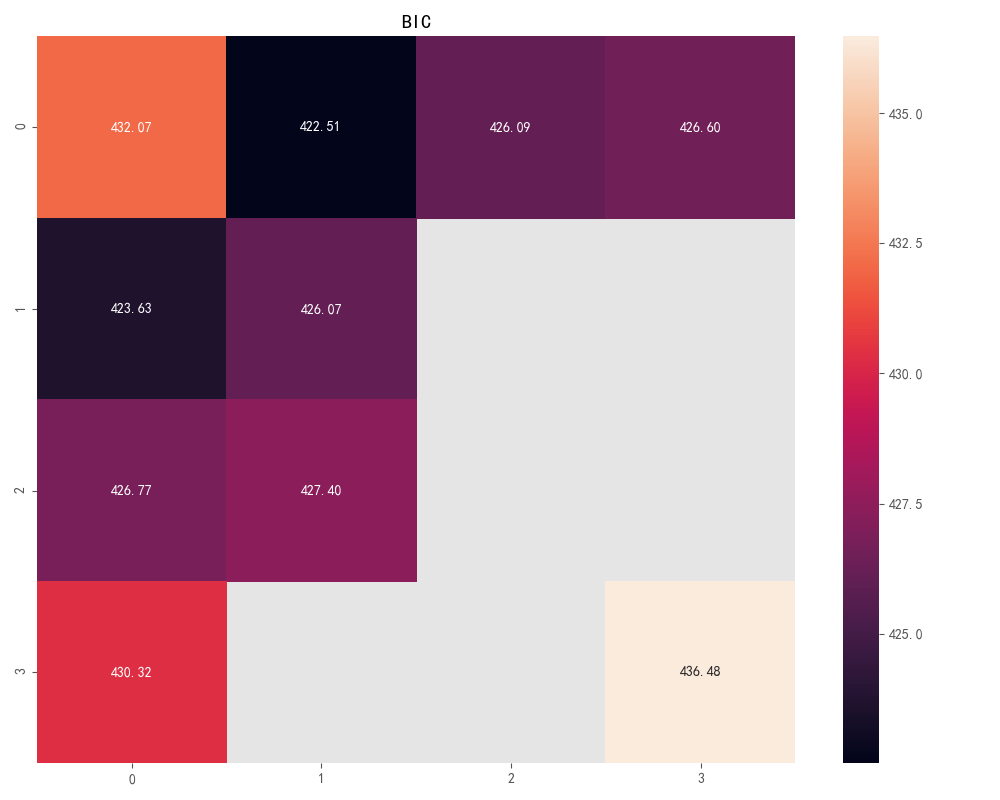
图8 矩阵热度图
P值为0、q值为1时最小BIC值为：430.1374。p、q定阶完成！
5.6 模型检验
用AR(1)模型拟合一阶差分后的序列，即对原始序列建立ARIMA(0,1,1)模型。虽然两种方法建立的模型是一样，但模型是非唯一的，可以检验ARIMA(1,1,0)和ARIMA(1,1,1)，这两个模型也能通过检验。
下面对一阶差分后的序列拟合AR(1)模型进行分析。
（1）模型检验。残差为白噪声序列，p值为：0.627016
（2）参数检验和参数估计见表10。
表10 模型参数
5.7 模型预测
1 model = ARIMA(data, (p, 1, q)).fit() # 建立ARIMA(0, 1, 1)模型 2 model.summary2() # 给出一份模型报告 3 model.forecast(5) # 作为期5天的预测，返回预测结果、标准误差、置信区间。
应用ARIMA(0,1,1)对表11中的2015/1/1~2015/2/6某餐厅的销售数据做为期5天的预测，结果如下。
表11 预测结果
需要说明的是，利用模型向前预测的时期越长，预测误差将会越大，这是时间预测的典型特点。
6 文献
王黎明，王连等. 应用时间序列分析
张良均，王路，谭立云，苏剑林. Python数据分析与挖掘实战
Complete guide to create a Time Series Forecast (with Codes in Python)
时间序列预测如何变成有监督学习问题？ - 云+社区 - 腾讯云
7 附录：程序及数据
说明：为了方便调用，我把所有程序都封装成函数，调用极其方便只用改动很小的参数。
1 # -*- coding:utf-8 -*- 2 # @Time : 2018/7/11 15:18 3 # @Author : yuanjing liu 4 # @Email : lauyuanjing@163.com 5 # @File : ts_arima.py 6 # @Software: PyCharm 7 # arima时序模型 8 9 import pandas as pd 10 import matplotlib.pyplot as plt 11 from matplotlib.pylab import style 12 from statsmodels.tsa.stattools import adfuller as ADF 13 from statsmodels.stats.diagnostic import acorr_ljungbox # 白噪声检验 14 from statsmodels.tsa.arima_model import ARIMA 15 import statsmodels.tsa.api as smt 16 import seaborn as sns 17 style.use('ggplot') 18 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 19 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 20 21 22 # 对原始数据进行ACF、PACF检验 23 def tsplot(y, lags=None, title='', figsize=(14, 8)): 24 fig = plt.figure(figsize=figsize) 25 layout = (2, 2) 26 ts_ax = plt.subplot2grid(layout, (0, 0)) 27 hist_ax = plt.subplot2grid(layout, (0, 1)) 28 acf_ax = plt.subplot2grid(layout, (1, 0)) 29 pacf_ax = plt.subplot2grid(layout, (1, 1)) 30 31 y.plot(ax=ts_ax) 32 ts_ax.set_title(title) 33 y.plot(ax=hist_ax, kind='hist', bins=25) 34 hist_ax.set_title('Histogram') 35 smt.graphics.plot_acf(y, lags=lags, ax=acf_ax) 36 smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax) 37 [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]] 38 sns.despine() 39 fig.tight_layout() 40 plt.show() 41 return ts_ax, acf_ax, pacf_ax 42 43 44 # *稳性检测(P值大于0.05，则存在单位根，是不*稳时间序列） 45 # adf_jy返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore 46 def steady(sdata): 47 adf_jy = ADF(sdata) # data[u'销量'] 48 adf_p_value = adf_jy[1] 49 return adf_jy, adf_p_value 50 51 52 # 白噪声检验 53 def w_noise(wdata): 54 w_noise = acorr_ljungbox(wdata, lags=1) # 返回统计量和p值 55 w_p_value = float(w_noise[1]) 56 return w_noise, w_p_value 57 58 59 # 差分后的结果（如果不*稳） 60 def ts_diff(ddata): 61 D_data = ddata.diff().dropna() # dropna是缺失值处理 62 D_data.columns = [u'1阶差分'] 63 return D_data 64 65 66 def ts_arima(tsdata, forenum=5): 67 tsdata = tsdata.astype(float) 68 # 定阶 69 D_data = ts_diff(tsdata) 70 pmax = int(len(D_data) / 10) # 一般阶数不超过length/10 71 qmax = int(len(D_data) / 10) # 一般阶数不超过length/10 72 bic_matrix = [] # bic矩阵 73 for p in range(pmax + 1): 74 tmp = [] 75 for q in range(qmax + 1): 76 try: # 存在部分报错，所以用try来跳过报错。 77 tmp.append(ARIMA(tsdata, (p, 1, q)).fit().bic) 78 except: 79 tmp.append(None) 80 bic_matrix.append(tmp) 81 82 bic_matrix = pd.DataFrame(bic_matrix) # 从中可以找出最小值 83 84 # 可视化BIC矩阵 85 fig, ax = plt.subplots(figsize=(10, 8)) 86 ax = sns.heatmap(bic_matrix, 87 mask=bic_matrix.isnull(), 88 ax=ax, 89 annot=True, 90 fmt='.2f', 91 ) 92 ax.set_title('BIC') 93 plt.show() 94 95 p, q = bic_matrix.stack().idxmin() # 先用stack展*，然后用idxmin找出最小值位置。 96 # print(u'BIC最小的p值和q值为：%s、%s' % (p, q)) 97 98 model = ARIMA(tsdata, (p, 1, q)).fit() # 建立ARIMA(0, 1, 1)模型 99 summary = model.summary2() # 给出一份模型报告 100 forecast = model.forecast(forenum) # 作为期forenum天的预测，返回预测结果、标准误差、置信区间。 101 return bic_matrix, p, q, model, summary, forecast 102 103 104 # 测试 105 # 读取数据 106 discfile = '../data/arima_data.xls' 107 forecastnum = 5 108 data = pd.read_excel(discfile, index_col=u'日期') 109 ddata = data[u'销量'] 110 # 检验 111 ts_ap = tsplot(ddata, title='A Given Training Series', lags=20) # ACF 和 PACF 检验 112 s_total, s_p = steady(ddata) # *稳性检验 113 w_total, w_p = w_noise(ddata) 114 # 差分 115 dif_data = ts_diff(ddata) 116 # arima模型 117 bic_matrix1, p1, q1, model1, summary, forecast = ts_arima(ddata)
转载说明
1、本人博客纯属技术积累和分享，欢迎大家评论和交流以求共同进步。
2、在无明确说明下，博客可以转载以供个人学习和交流，但是要附上出处。
3、如果原创博客使用涉及商业/公司行为请邮件(1547364995@qq.com)告知，一般情况均会及时回复同意。
4、如果个人博客中涉及他人文章我会尽力注明出处，但受限于能力并不能保证所有引用之处均能够注明出处，如有冒犯，请您及时邮件告知以便修改，并于此提前向您道歉。
5、转载过程中如有涉及他人作品请您与作者联系。
6、所有文章（不限于原创）仅为个人见解，个人只能尽量保证正确，如有错误您需要自负责任，并请您留下评论提出错误之处以便及时更正，惠泽他人，谢谢
