时间序列算法理论及python实现(1-算法理论部分)
正文
如果你在寻找时间序列是什么?如何实现时间序列?那么请看这篇博客,将以通俗易懂的语言,全面的阐述时间序列及其python实现。
就餐饮企业而言,经常会碰到如下问题。
由于餐饮行业是胜场和销售同时进行的,因此销售预测对于餐饮企业十分必要。如何基于菜品历史销售数据,做好餐销售预测,以便减少菜品脱销现象和避免因备料不足而造成的生产延误,从而减少菜品生产等待时间,提供给客户更优质的服务,同事可以减少安全库存量,做到生产准时制,降低物流成本
餐饮销售预测可以看作是基于时间序列的短期数据预测,预测对象为具体菜品销售量
常用按时间序列排列的一组随机变量,来表示一个随机事件的时间序列,简记为;用或表示该随机序列的n个有序观察值,称之为序列长度为n的观察值序列
本博文应用时间序列分析的目的就是给定一个已被观测了的时间序列,预测该序列的未来值。
1 时间序列算法
常用的时间序列模型见表1.
表1 常用时间序列模型
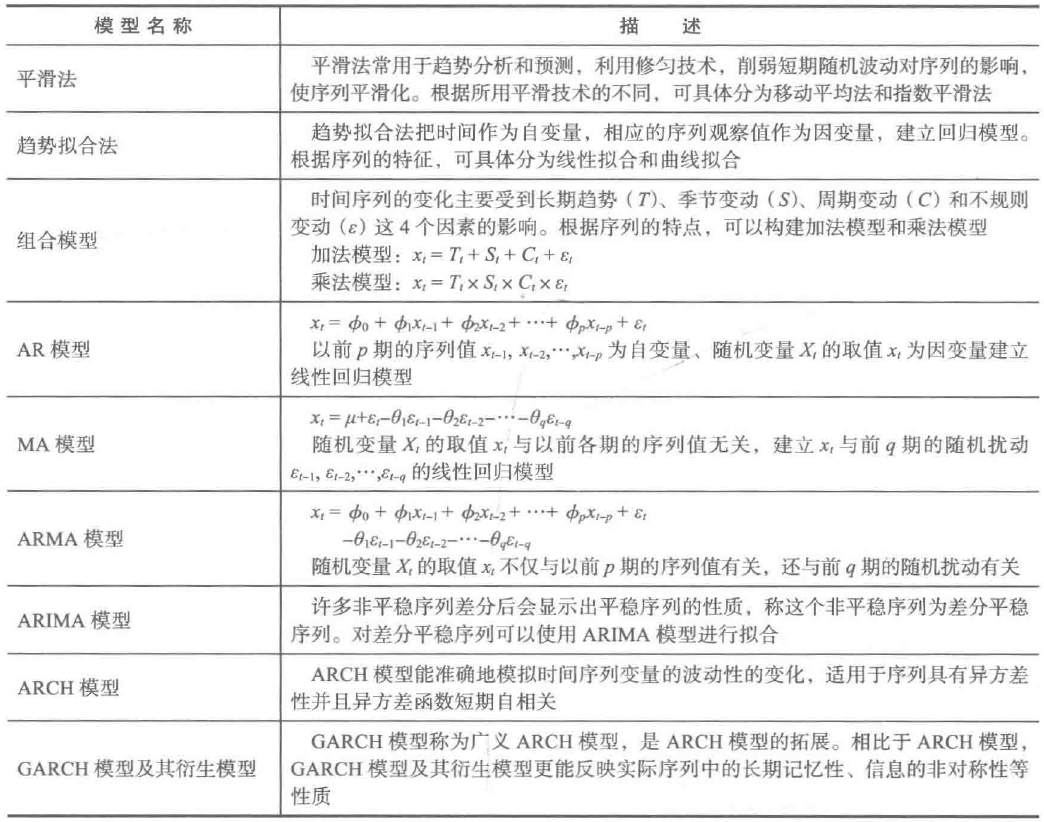
本博文将重点介绍AR模型、MA模型、ARMA模型和ARINA模型。
2 时间序列的预处理
拿到一个观察序列后,首先对它的纯随机性和平稳性进行检验,这两个重要的检验成为序列的预处理。根据检验结果可以将序列分为不同夫的类型,对不同类型的序列会采取不同的分析方法。
对于纯随机序列,又称为白噪声序列,序列的各项之间没有任何相关关系,序列在进行完全无序的随机波动,可以终止对该序列的分析。白噪声序列是没有信息可提取的平稳序列。
对于平稳非白噪声序列,它的均值和方差是常数,现已有一套非常成熟的平稳序列的的建模方法。通常是建立一个线性模型来拟合该序列的发展,借此提取该序列有用信息。ARMA模型是最常用的平稳序列拟合模型。
对于非平稳序列,由于它的均值和方差不稳定,处理方法一般是将其转变为平稳序列,这样就可以应用有关平稳时间序列的分析方法,如建立ARMA模型来进行相应的研究。如果一个时间序列经差分运算后具有平稳性,则该序列为差分平稳序列,可以使用ARIMA模型进行分析。
2.1 平稳性检验
2.1.1 平稳时间序列的定义
对于随机变量X,可以计算其均值(数学期望)、方差;对于两个随机变量X和Y,可以计算X,Y的协方差和相关系数,他们度量了两个不同事件之间的相互影响程度。
对于时间序列,任意时刻的序列值都是一个随机变量,每一个随机变量都会有均值和方差,记的均值为,方差为;任取,定义序列的自协方差函数和自相关函数(特别地,),之所以称它们为自协方差和自相关系数,是因为它们衡量的是同一个事件在两个不同时期(时刻t和s)之间的相关程度,形象地讲就是度量自己过去的行为对自己现在的影响。
如果时间序列在某一常数附近波动且波动范围有限,即有常数均值和常数方差,并且延迟k期的序列变量的自协方差和自相关系数是相等的或者说延迟k期的序列变量之间的影响程度是一样的,则称为平稳序列。
2.1.2 平稳性的检验
对序列的平稳性的检验有两种检验方法,一种是根据时序图和自相关图的特征做出判断的图检验,该方法操作简单、应用广泛,缺点是带有主观性;另一种是构造检验统计量进行检验的方法,目前最常用的方法是单位根检验
(1) 时序图检验
根据平稳时间序列的均值和方差都为常数的性质,平稳序列的时序图显示该序列值始终在一个常数附近随机波动,而且波动的范围有界;如果有明显的趋势性或周期性,那它通常不是平稳序列。
(2) 自相关图检验
平稳序列具有短期相关性,这个性质表明对平稳序列而言通常只有近期的序列值对现时值得影响比较明显,间隔越远的过去值对现时值的影响越小。随着延迟期数k的增加,平稳序列的自相关系数(延迟k期)会比较快的衰减趋向于零,并在零附近随机波动,而非平稳序列的自相关系数衰减的速度比较慢,这就是利用自相关图进行平稳性检验的标准。
(3) 单位根检验
单位根检验是检验序列中是否存在单位根,如果存在单位根就是非平稳时间序列了。
2.2 纯随机性检验
如果一个序列是纯随机序列,那么它的序列值之间应该没有任何关系,即满足这是一种理论上才会出现的理想状态,实际上纯随机序列的样本自相关系数不会绝对为零,但是很接近零,并在零附近随机波动。
纯随机性检验也称白噪音检验,一般是构造检验统计量来检验序列的纯随机性,常用的检验统计量有Q统计量、LB统计量,由样本各延迟期数的自相关系数可以计算得到检验统计量,然后计算出对应的p值,如果p值显著大于显著性水平,则表示该序列不能拒绝纯随机的原假设,可以停止对该序列的分析。
3 平稳时间序列分析
ARMA模型的全称是自回归移动平均模型,它是目前最常用的拟合平稳序列的模型。它又可以细分为AR模型、MA模型和ARMA模型三大类。都可以看作是多元线性回归模型。
3.1 AR模型
具有如下结构的模型称为p阶自回归模型,简记为。
即在t时刻的随机变量的取值是前期的多元线性回归,认为主要是受过去期的序列值的影响。误差项是当期的随机干扰,为零均值白噪声序列。
平稳AR模型的性质见表2.
表2 平稳模型的性质

3.1.1 均值
对满足平稳性条件的模型的的方程,两边取期望,得:
已知,所以有,解得:
3.1.2 方差
平稳模型的方差有界,等于常数。
3.2 MA模型
具有如下结构的模型称为阶自回归模型,简记为。
即在t时刻的随机变量的取值是前q期的随机扰动的多元线性函数,误差项是当期的随机干扰,为零均值白噪声序列,是序列的均值。认为主要是受过去q期的误差项的影响。
平稳模型的性质见表3.
表3 平稳模型的性质

3.3 ARMA模型
具有如下结构的模型称为自回归移动平均模型,简记为。
即在t时刻的随机变量的取值是前期和前期的多元线性函数,误差项是当期的随机干扰,为零均值白噪声序列。认为主要是受过去期的序列值和过去期的误差项的共同影响。
特别的,当时,是模型;当时,是模型
平稳的性质见表4.
表4 平稳模型的性质

3.4 相关评判方法介绍
3.4.1 自相关系数(ACF)
平稳模型的自相关系数呈指数的速度锐减,始终有非零取值,不会在大于某个常数之后就恒等于零,这个性质就是平稳模型的自相关系数具有拖尾性。
3.4.2 偏自相关系数(PACF)
对于一个平稳模型,求出延迟k期自相关系数时,实际上的得到的并不是
与之间单纯的相关关系,因为同时还会收到中间个随机变量的影响,所以自相关系数里实际上掺杂了其他变量对与的相关影响,为了单纯地测度对的影响,引进偏自相关系数的概念。
可以证明平稳模型的偏自相关系数具有阶截尾性。这个性质连同前面的自相关系数的拖尾性是模型重要的识别依据。
3.4.3 截尾和拖尾
(1)p阶自回归模型
AR(p)模型的偏自相关函数PACF在p阶之后应为零,称其具有截尾性;
AR(p)模型的自相关函数ACF不能在某一步之后为零(截尾),而是按指数衰减(或成正弦波形式),称其具有拖尾性。
(2)q阶移动平均模型
MA(q)模型的自相关函数ACF在q阶之后应为零,称其具有截尾性;
MA(q)模型的偏自相关函数PACF不能在某一步之后为零(截尾),而是按指数衰减(或成正弦波形式),称其具有拖尾性。
3.4.4 截尾和拖尾判断
(1)如果样本自相关系数(或偏自相关系数)在最初的d阶明显大于2倍标准差范围,而后几乎95%的样本自相关(偏自相关)系数都落在2倍标准差范围以内,而且由非零自相关(偏自相关)系数衰减为小值波动的过程非常突然,这时,通常视为自相关(偏自相关)系数截尾。
(2)如果有超过5%的样本相关系数落在2倍标准差范围以外,或者是由显著非零的相关函数衰减为小值波动的过程比较缓慢或者非常连续,这时,通常视为相关系数不截尾。
3.4 平稳时间序列建模
某个时间序列经过预处理,被判定为平稳非白噪声序列,就可以利用ARMA模型进行建模。计算出平稳非白噪声序列的自相关系数和偏自相关系数,再由模型、模型和模型的自相关系数和偏自相关系数的性质,选择合适的模型。平稳时间序列建模步骤如图1所示。
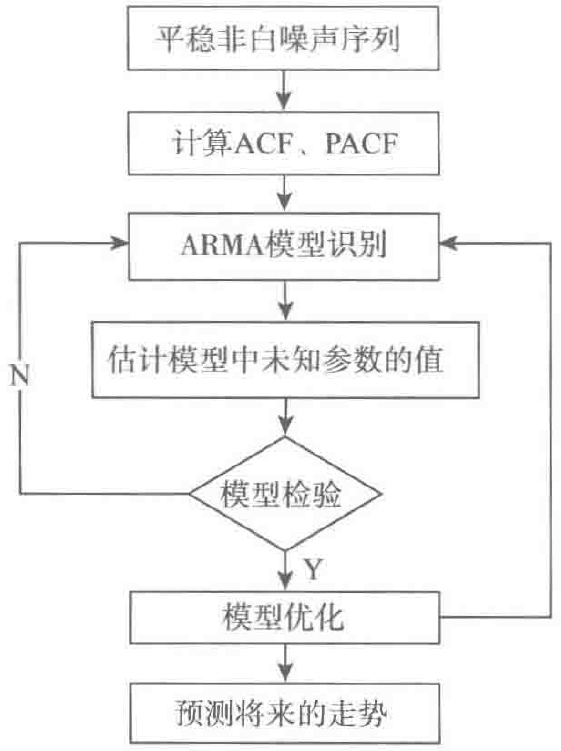
图1 平稳时间序列ARMA模型建模步骤
3.4.1 计算ACF和PACF
先计算非平稳白噪声序列的自相关系数(ACF)和偏自相关系数(PACF)。
3.4.2 ARMA(p,d,q)模型识别
也称为模型定阶,由模型、模型和的自相关系数和偏自相关系数的性质,选择合适的模型。识别的原则见表5.
表5 ARMA模型识别原则

以这个表来确定和,p值确定看PACF,q值确定看ACF,截尾的意义简而言之,就是落到95%置信区间内。
其次,模型中d,主要指d阶差分之后,模型能通过平稳性检验,此时d就是合适的参数。
4 非平稳时间序列分析
前面介绍了对平稳时间序列进行分析的方法。实际上,在自然界中绝大部分序列都是非平稳的。因而对非平稳序列的分析更普遍、更重要,创造出来的分析方法也更多。
对非平稳时间序列的分析方法可以分为确定性因素分解的时序分析和随机时序分析两大类。
确定性因素分解的方法把所有序列的变化都归结为4个因素(长期趋势、季节变动、循环变动和随机波动)的综合影响,其中长期趋势和季节变动的规律性信息通常比较容易提取,而由随机因素导致的波动则非常难确定和分析,对随机信息浪费严重,会导致模型拟合精度不够理想。
随机时序分析法的发展就是为了弥补确定性因素分解方法的不足。根据时间序列的不同特点,随机时序分析可以建立的模型有ARIMA模型、残差自回归模型、季节模型、异方差模型等。本节重点介绍使用ARIMA模型对非平稳时间序列进行建模的方法。
4.1 差分运算
4.1.1 p阶差分
相距p期的两个序列值之间的减法运算称为p阶差分运算。
4.1.2 k步差分
相距k期的两个序列值之间的减法运算称为k步差分运算。
4.2 ARIMA模型
差分运算具有强大的确定性信息提取能力,许多非平稳序列差分后会显示出平稳序列的性质,这时称这个非平稳序列为差分平稳序列。对差分平稳序列可以使用ARMA模型进行拟合。ARIMA模型的实质就是差分运算与ARMA模型的组合,掌握了ARMA模型的建模方法和步骤之后,对序列建立ARIMA模型是比较简单的。
差分平稳时间序列建模步骤如图2所示。
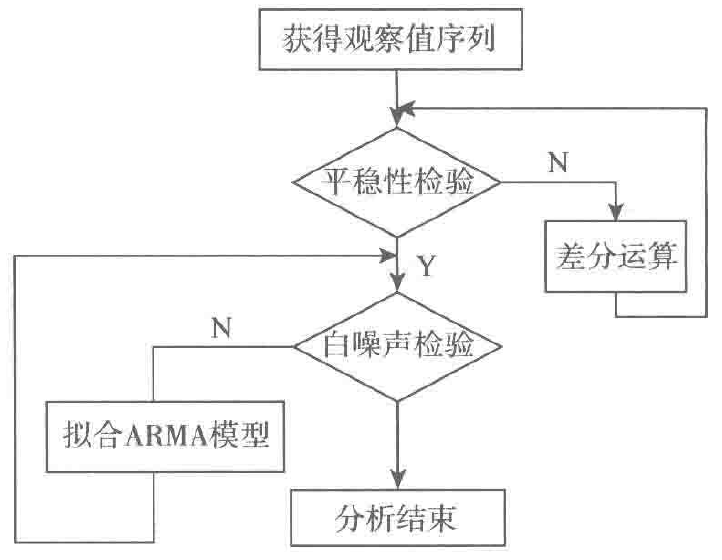
图2 差分平稳时间序列建模步骤
4.2.1 计算ACF和PACF
4.2.2 ARIMA模型识别
也称为模型定阶,由模型、模型和的自相关系数和偏自相关系数的性质,选择合适的模型。识别的原则见表5.
表5 ARMA模型识别原则

以这个表来确定和,p值确定看PACF,q值确定看ACF,截尾的意义简而言之,就是落到95%置信区间内。
其次,模型中d,主要指d阶差分之后,模型能通过平稳性检验,此时d就是合适的参数。
4.2.3 使用AIC与BIC模型选择:选择更简单的模型
(1)AIC:赤池信息准则(Akaike Information Criterion,)
(2)BIC:贝叶斯信息准则(Bayesian Information Criterion,)
其中,为模型参数个数,为样本数量,为似然函数
这个准则是为了选择更简单的模型,当p和q有多种组合,我们不确定哪一个组合更优,我们就可以观察模型的AIC和BIC参数,以此来找出使模型最优的p和q,这一系列过程可以在程序中实现自动化进行模型定阶,将在python实现部分,进行阐述。
4.2.4 模型检验
我们对于某个预想为目标的模型判断是否结果可用,就需要对模型进行诊断,如果诊断不合格,这时候需要重新选择模型,如果模型可用,就可以进行下一步的预测操作,其中模型诊断一般包括两个方面,一个是残差的检验分析,一个是关于模型过度拟合和参数冗余的问题,总体原则是尽量选择简单的模型。
(1)残差检验分析
对于残差检验分析还有很多的方法,这里只列出常见的方法以及要检验的内容:
- 残差图肉眼简单查看;
- ARIMA模型的残差是否是平均值为0且方差为常数的正态分布;
- QQ图:线性即正态分布;
- Ljung-Box检验:独立性
(2)过度拟合和参数冗余
对于统计建模或者是机器学习,我们一般都需要模型过拟合的问题,同样的,于时间序列而言,过度拟合和参数冗余也是不容忽视的问题:
- 在过度拟合时,不要同时增加AR和MA部分的阶数
- 例如:如果拟合了MA(1)模型后,残差在2阶滞后处仍存在明显的相关性,那么应该尝试MA(2),而不是ARMA(1,1)模型。
4.2.5 模型优化
一般情况下,安装步骤系统选择好模型之后,模型的方法不存在太大的问题,主要是参数优化方面,我们使用AIC和BIC来确定最优模型的参数,是较为准确的,如果在使用AIC和BIC确定好了参数之后,模型还是没有通过以上检验,则需要考虑模型方法是否选择正确,模型使用是否是合适的情况。
4.2.6 模型应用:进行短期预测
当上面的步骤走完之后,就可以对数据进行预测了,也就是时间序列建模的主要目标之一,预测该序列未来的取值,此外我们要评估预测的精度。一般采用最小均方误差标准。
5 Python实现ARIMA模型
由于写在同一篇博客篇幅太长,不利用阅读,这部分内容请移步我的另一篇博文:时间序列算法理论及python实现(2-python实现) - 知-青 - 博客园
6 Python主要时序模式算法
同理,由于写在同一篇博客篇幅太长,不利用阅读,这部分内容请移步我的另一篇博文:
7 文献
王黎明,王连等. 应用时间序列分析
张良均,王路,谭立云,苏剑林. Python数据分析与挖掘实战
Complete guide to create a Time Series Forecast (with Codes in Python)
时间序列预测如何变成有监督学习问题? - 云+社区 - 腾讯云

转载说明
1、本人博客纯属技术积累和分享,欢迎大家评论和交流以求共同进步。
2、在无明确说明下,博客可以转载以供个人学习和交流,但是要附上出处。
3、如果原创博客使用涉及商业/公司行为请邮件(1547364995@qq.com)告知,一般情况均会及时回复同意。
4、如果个人博客中涉及他人文章我会尽力注明出处,但受限于能力并不能保证所有引用之处均能够注明出处,如有冒犯,请您及时邮件告知以便修改,并于此提前向您道歉。
5、转载过程中如有涉及他人作品请您与作者联系。
6、所有文章(不限于原创)仅为个人见解,个人只能尽量保证正确,如有错误您需要自负责任,并请您留下评论提出错误之处以便及时更正,惠泽他人,谢谢




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统