机器学习速成笔记四

特征组合是指两个或多个特征相乘形成的合成特征。特征的相乘组合可以提供超出这些特征单独能够提供的预测能力。

特征组合 (Feature Crosses)：对非线性规律进行编码

请看如下示例，我们做出如下假设：

• 蓝点代表生病的树。
• 橙点代表健康的树。

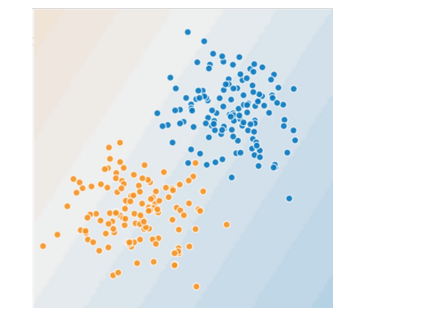
您可以画一条线将生病的树与健康的树清晰地分开吗？当然可以。这是个线性问题。这条线并不完美。有一两棵生病的树可能位于“健康”一侧，但您画的这条线可以很好地做出预测。
现在再来看下图：

您可以画一条直线将生病的树与健康的树清晰地分开吗？不，您做不到。这是个非线性问题。您画的任何一条线都不能很好地预测树的健康状况。

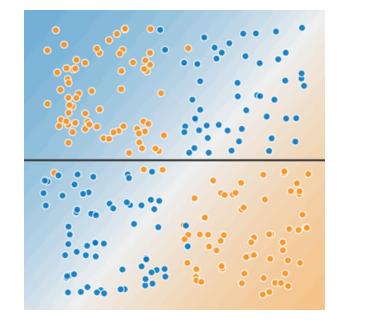
要解决上图所示的非线性问题，可以创建一个特征组合。特征组合是指通过将两个或多个输入特征相乘来对特征空间中的非线性规律进行编码的合成特征。“cross”（组合）这一术语来自 cross product（向量积）。我们通过将\(x_1\) 与\(x_2\) 组合来创建一个名为\(x_3\) 的特征组合：

\[x_3 = x_1x_2 \]

我们像处理任何其他特征一样来处理这个新建的 \(x_3\) 特征组合。线性公式变为：

\[y = b + w_1x_1 + w_2x_2 + w_3x_3 \]

线性算法可以算出\(w_3\)的权重，就像算出\(w_1\)和\(w_2\)的权重一样。换言之，虽然\(w_3\)表示非线性信息，但不需要改变线性模型的训练方式来确定\(w_3\)的值。

特征组合的种类

我们可以创建很多不同种类的特征组合。例如：

• [A X B]：将两个特征的值相乘形成的特征组合。
• [A x B x C x D x E]：将五个特征的值相乘形成的特征组合。
• [A x A]：对单个特征的值求平方形成的特征组合。

通过采用随机梯度下降法，可以有效地训练线性模型。因此，在使用扩展的线性模型时辅以特征组合一直都是训练大规模数据集的有效方法。

特征组合 (Feature Crosses)：组合独热矢量

到目前为止，我们已经重点介绍了如何对两个单独的浮点特征进行特征组合。在实践中，机器学习模型很少会组合连续特征。不过，机器学习模型却经常组合独热特征矢量，将独热特征矢量的特征组合视为逻辑连接。例如，假设我们具有以下两个特征：国家/地区和语言。对每个特征进行独热编码会生成具有二元特征的矢量，这些二元特征可解读为 country=USA, country=France 或 language=English, language=Spanish。然后，如果您对这些独热编码进行特征组合，则会得到可解读为逻辑连接的二元特征，如下所示：

country:usa AND language:spanish

再举一个例子，假设您对纬度和经度进行分箱，获得单独的独热 5 元素特征矢量。例如，指定的纬度和经度可以表示如下：

  binned_latitude = [0, 0, 0, 1, 0]
  binned_longitude = [0, 1, 0, 0, 0]

假设您对这两个特征矢量创建了特征组合：

 binned_latitude X binned_longitude

此特征组合是一个 25 元素独热矢量（24 个 0 和 1 个 1）。该组合中的单个 1 表示纬度与经度的特定连接。然后，您的模型就可以了解到有关这种连接的特定关联性。假设我们更粗略地对纬度和经度进行分箱，如下所示：

binned_latitude(lat) = [
  0  < lat <= 10
  10 < lat <= 20
  20 < lat <= 30
]

binned_longitude(lon) = [
  0  < lon <= 15
  15 < lon <= 30
]

针对这些粗略分箱创建特征组合会生成具有以下含义的合成特征：

binned_latitude_X_longitude(lat, lon) = [
  0  < lat <= 10 AND 0  < lon <= 15
  0  < lat <= 10 AND 15 < lon <= 30
  10 < lat <= 20 AND 0  < lon <= 15
  10 < lat <= 20 AND 15 < lon <= 30
  20 < lat <= 30 AND 0  < lon <= 15
  20 < lat <= 30 AND 15 < lon <= 30
]

线性学习器可以很好地扩展到大量数据。对大规模数据集使用特征组合是学习高度复杂模型的一种有效策略。神经网络可提供另一种策略。

简化正则化 (Regularization for Simplicity)：L₂ 正则化

请查看以下泛化曲线，该曲线显示的是训练集和验证集相对于训练迭代次数的损失。

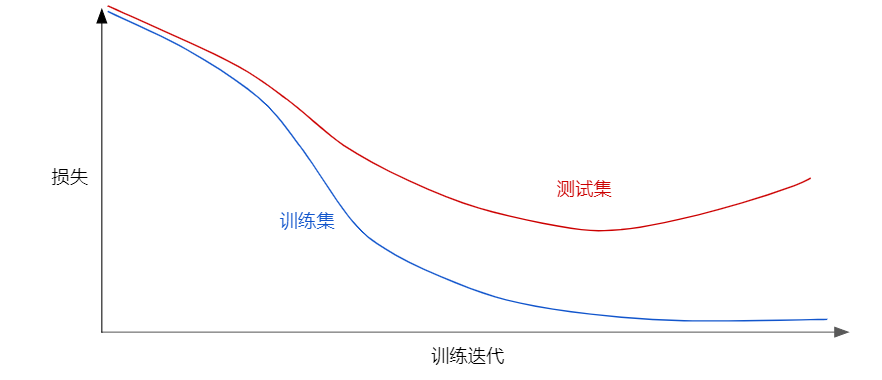
上图显示的是某个模型的训练损失逐渐减少，但验证损失最终增加。换言之，该泛化曲线显示该模型与训练集中的数据过拟合。根据奥卡姆剃刀定律，或许我们可以通过降低复杂模型的复杂度来防止过拟合，这种原则称为正则化。也就是说，并非只是以最小化损失（经验风险最小化）为目标：

\[minimize(Loss(Data|Model)) \]

而是以最小化损失和复杂度为目标，这称为结构风险最小化：

\[minimize(Loss(Data|Model) + complexity(Model)) \]

现在，我们的训练优化算法是一个由两项内容组成的函数：一个是损失项，用于衡量模型与数据的拟合度，另一个是正则化项，用于衡量模型复杂度。下面介绍两种衡量模型复杂度的常见方式（这两种方式有些相关）：

• 将模型复杂度作为模型中所有特征的权重的函数。
• 将模型复杂度作为具有非零权重的特征总数的函数。

如果模型复杂度是权重的函数，则特征权重的绝对值越高，对模型复杂度的贡献就越大。我们可以使用 L2 正则化公式来量化复杂度，该公式将正则化项定义为所有特征权重的平方和：

\[L_2 regularization term = \lvert\lvert w \rvert\rvert^2_2 = w^2_1 + w^2_2 + \dots +w^2_n \]

在这个公式中，接近于 0 的权重对模型复杂度几乎没有影响，而离群值权重则可能会产生巨大的影响。例如，某个线性模型具有以下权重：

\[\{ w_1 = 0.2, w_2=0.5, w_3=5,w_4=1,w_5=0.25,w_6=0.75 \} \]

L2 正则化项为 26.915：

\[w_1^2 + w_2^2 + w_3^2 + w_4^2 + w_5^2 + w_6^2 = 0.2^2 + 0.5^2 + 5^2 + 1^2 + 0.25^2 + 0.75^2 = 26.915 \]

但是 \(w_3\) 的平方值为 25，几乎贡献了全部的复杂度。所有 5 个其他权重的平方和对 L2 正则化项的贡献仅为 1.915

简化正则化 (Regularization for Simplicity)：Lambda

模型开发者通过以下方式来调整正则化项的整体影响：用正则化项的值乘以名为 lambda（又称为正则化率）的标量。也就是说，模型开发者会执行以下运算：

\[minimize(Loss(Data|Model) + \lambda complexity(Model)) \]

执行 L2 正则化对模型具有以下影响:

• 使权重值接近于 0（但并非正好为 0）
• 使权重的平均值接近于 0，且呈正态（钟形曲线或高斯曲线）分布。

增加 lambda 值将增强正则化效果。 例如，lambda 值较高的权重直方图可能会如下图所示。

降低 lambda 的值往往会得出比较平缓的直方图，如下图所示。

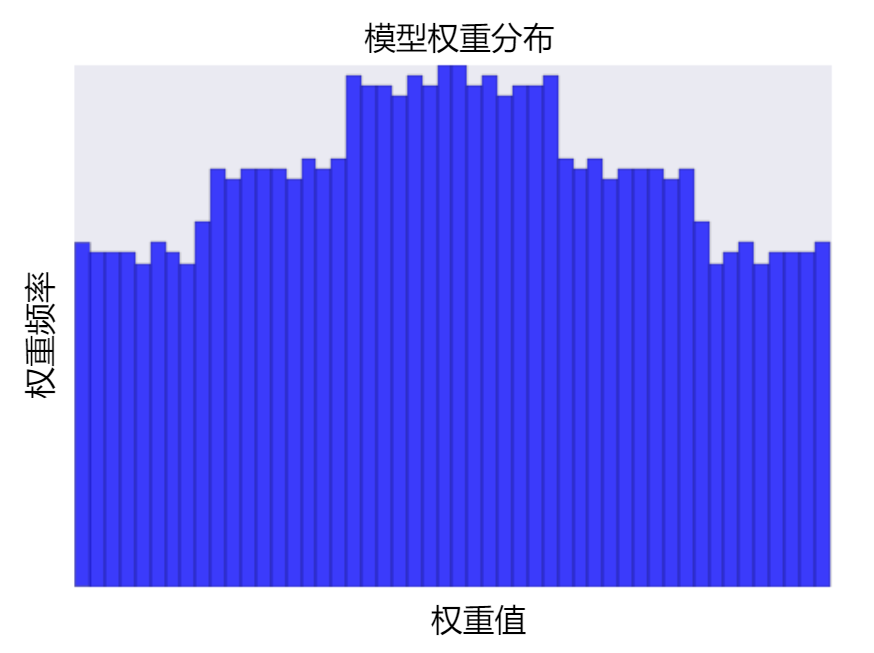
在选择 lambda 值时，目标是在简单化和训练数据拟合之间达到适当的平衡：

• 如果您的 lambda 值过高，则模型会非常简单，但是您将面临数据欠拟合的风险。您的模型将无法从训练数据中获得足够的信息来做出有用的预测。
• 如果您的 lambda 值过低，则模型会比较复杂，并且您将面临数据过拟合的风险。您的模型将因获得过多训练数据特点方面的信息而无法泛化到新数据

注意：将 lambda 设为 0 可彻底取消正则化。 在这种情况下，训练的唯一目的将是最小化损失，而这样做会使过拟合的风险达到最高。

理想的 lambda 值生成的模型可以很好地泛化到以前未见过的新数据。 遗憾的是，理想的 lambda 值取决于数据，因此您需要手动或自动进行一些调整。
学习速率和 lambda 之间存在密切关联。强 L2 正则化值往往会使特征权重更接近于 0。较低的学习速率（使用早停法）通常会产生相同的效果，因为与 0 的距离并不是很远。 因此，同时调整学习速率和 lambda 可能会产生令人混淆的效果。
早停法指的是在模块完全收敛之前就结束训练。在实际操作中，我们经常在以在线（连续）方式进行训练时采取一些隐式早停法。也就是说，一些新趋势的数据尚不足以收敛。

如上所述，更改正则化参数产生的效果可能会与更改学习速率或迭代次数产生的效果相混淆。一种有用的做法（在训练一批固定的数据时）是执行足够多次迭代，这样早停法便不会起作用。