bzoj1468 Tree*
题意:
给你一棵TREE,以及这棵树上边的距离.问有多少对点它们两者间的距离小于等于K
题解:
点分治:先建树,然后分两步
1、计算当前点所在子树中符合条件的点对
2、在当前点的子树中选一个点作为根节点,递归这些根结点
如何求当前点所在子树中符合条件的点对数呢?
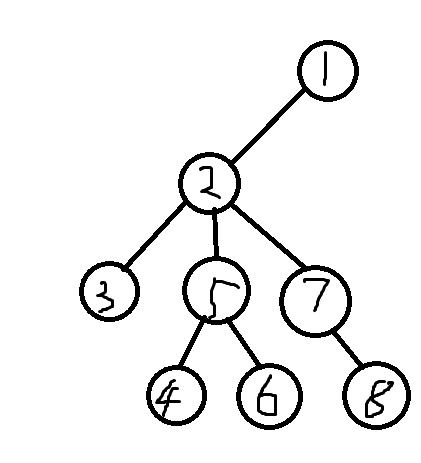
先通过dfs求出从当前节点到所在子树各节点的距离,然后用排序+两头计算法计算出从某节点到当前节点再到另一节点的距离满足条件的点对。但是,这样做是有缺陷的。
如图,当前节点为2,就可能求出4-5-2-5-6这样不存在的情况,怎么办呢?设此点对数为x。我们可以对每个子节点进行这样的计算:将该子节点的初始距离数组d[x]置为当前节点到该子节点的距离,求出该子节点到其所在子树所有点的距离,然后用与刚才类似的方法算出与该子节点相关的点对数设为yi。将x减掉所有子节点的yi得到的值就是真实的点对数。
刚才计算子节点的操作实际上求得的就是经过该子节点的不存在的点对数(如中间经过5-2-5的点对)。
前面述说的两个操作类似,可以合并成一个函数getdis,前者操作就是把当前节点的初始距离数组d[x]置为0。具体看代码。
选哪个节点作为根节点?
引入一个概念:树的重心:找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,生成的多棵树尽可能平衡。
很明显,我们找根就要找树的重心。怎么求树的重心呢?用dfs求出当前节点所在子树的每个节点最大子树的最小值即可,注意树的形态是不一定的,所以除了逻辑上的儿子sz[i]还有sm-sz[x]
同时还有一些细节,比如vis数组,使搜索时不要搜到想搜的子树之外的节点
时间复杂度?work执行n次,calc执行O(log2n)次(因为根为树的重心),getroot和getdis总共执行了O(nlog2n)次,所以总复杂度为O(nlog2n)(其实我也不知道为什么复杂度是这个,但它就是这个……)
代码:
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #define INF 0x3fffffff 5 #define inc(i,j,k) for(int i=j;i<=k;i++) 6 #define visit(i,j) for(int i=g[j];i!=-1;i=es[i].n) 7 #define N 40010 8 using namespace std; 9 10 int n,k,ans; 11 12 struct e{int t,w,n;}; e es[N*2]; int ess,g[N]; 13 inline void pe(int f,int t,int w){es[++ess]=(e){t,w,g[f]}; g[f]=ess; es[++ess]=(e){f,w,g[t]}; g[t]=ess;} 14 15 int root,sm,mn,szs,d[N],sz[N],data[N]; bool vis[N]; 16 void getroot(int x,int fa){ 17 sz[x]=1; int mx=0; 18 visit(i,x)if(! vis[es[i].t]&&es[i].t!=fa){getroot(es[i].t,x); sz[x]+=sz[es[i].t]; mx=max(mx,sz[es[i].t]);} 19 mx=max(mx,sm-sz[x]); if(mx<mn)root=x,mn=mx; 20 } 21 void getdis(int x,int fa){ 22 data[++szs]=d[x]; 23 visit(i,x)if(! vis[es[i].t]&&es[i].t!=fa){d[es[i].t]=d[x]+es[i].w; getdis(es[i].t,x);} 24 } 25 int calc(int x,int st){ 26 d[x]=st; szs=0; getdis(x,-1); sort(data+1,data+szs+1); int l=1,r=szs,a=0; 27 while(l<r){if(data[l]+data[r]<=k)a+=(r-l),l++;else r--;} 28 return a; 29 } 30 void work(int x){ 31 ans+=calc(x,0); vis[x]=1; 32 visit(i,x)if(!vis[es[i].t]){ans-=calc(es[i].t,es[i].w); root=es[i].t; sm=sz[es[i].t]; mn=INF; getroot(es[i].t,x); work(root);} 33 } 34 35 int main(){ 36 scanf("%d",&n); ess=0; memset(g,-1,sizeof(g)); 37 inc(i,1,n-1){int a,b,c; scanf("%d%d%d",&a,&b,&c); pe(a,b,c);} scanf("%d",&k); 38 memset(vis,0,sizeof(vis)); root=1; mn=INF; getroot(1,-1); ans=0; work(root); printf("%d\n",ans); 39 return 0; 40 }
20151210



