[手游]碧蓝档案pt活动材料刷取的数学模型与Lingo程序求解

1. 问题

在碧蓝档案中的pt活动中，由于Quest最后一关会掉落所有活动材料，与前面的特定材料关刷取时不容易把控合理的刷取次数，从而造成材料的溢出和资源的浪费。即使商店对于溢出的材料有回收机制（很亏），通过合理的规划刷取使得资源的利用最大化是值得讨论的。

以本次日服复刻梦幻岛活动为例

2. 定义

碧蓝档案中的pt活动指的是：在活动时间内，使用体力重复刷取一组特定关卡，获得固定的活动材料去商店兑换奖励。pt活动有以下特点：

1. 当关卡的加成不变时，每次刷取关卡的活动材料的数量时固定的（通用素材随机掉落）。
2. 当玩家解锁扫荡时，刷取关卡的次数仅受限于玩家的体力。
3. 不论回收机制，搬空商店需要的材料是有限的，过多刷取的材料会被浪费。

活动的Quest关卡为活动材料的刷取关卡，其分布有一定的规律性：在一组关卡中，除最后一关外每关均会掉落少量pt点数和一种活动材料，该组最后一关会掉落大量pt点和少量所有活动材料。Quest关卡包含了不同难度的关卡组，关卡的难度与收益成正比。考虑到刷取效率和大部分玩家的等级，计算刷取的关卡组选用最高难度。

本活动最高难度关组为Quest9，Quest10，Quest11，Quest12

3. 模型建立

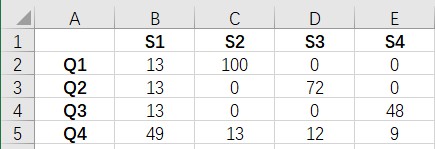
收益表取自本人队伍加成的情况，可能与各位不同。

决策变量：设关卡q1, q2, …, qn的刷取次数分别为x1, x2, …, xn；
目标函数：设刷取消耗的总体力为z，为各关卡刷取次数与对应体力花费乘积之和；
约束条件：刷取的活动材料数量不小于期望值，各关卡的刷取次数为正整数；
由此得如下整数线性规划模型：

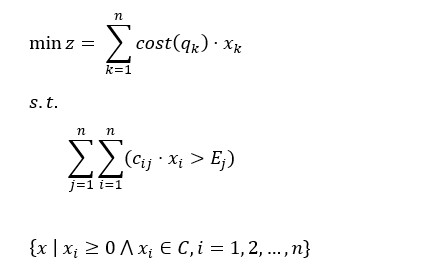
4. 模型求解

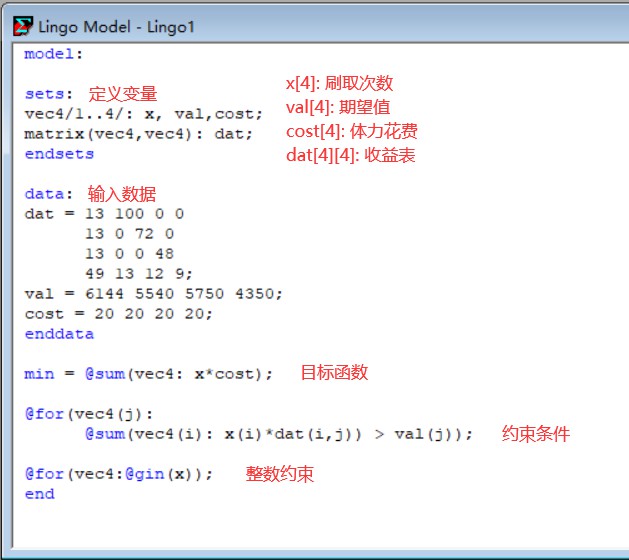
编写的Lingo程序（收益表dat和活动材料期望值val使用的是自己的数据，结果仅供参考）

求解结果：

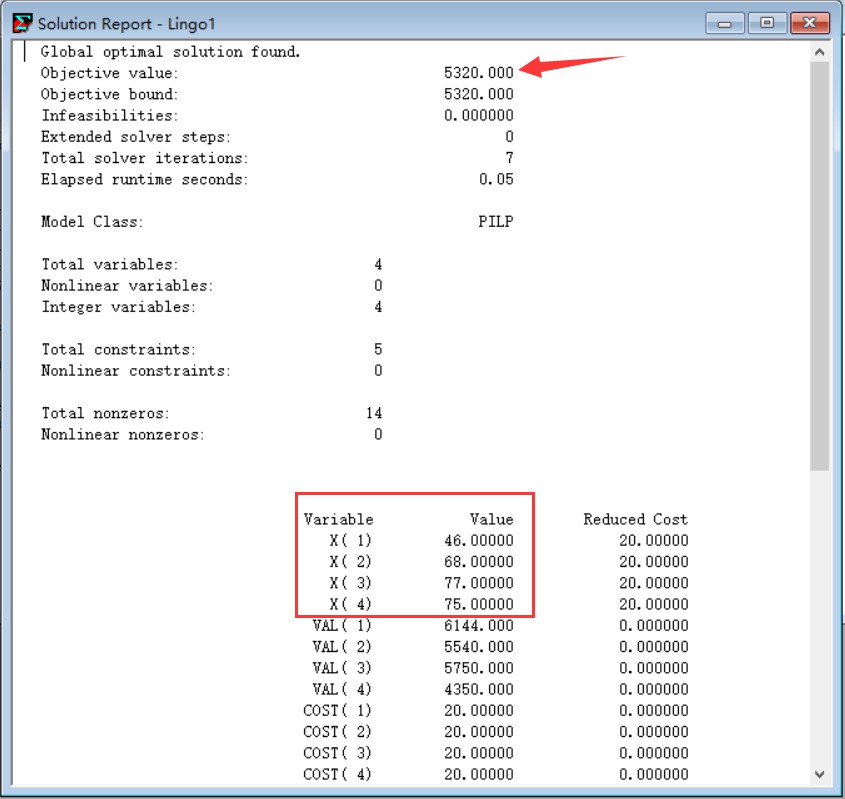
我们只需要关注目标值（箭头）和用于存储求解结果的变量X（红框）。
目标值显示最小需要消耗的体力是5320。当需求体力超过自己的体力获取能力时，需要重新调整期望值。
X(1)—X(4)的值显示达到期望值的刷取次数，对应游戏中Quest9刷46次，Quest10刷68次，Quest11刷77次，Quest12刷75次。若出现小数则可能是未加上整数约束@gin()。

*活动结束前显然凑不出5k体力，故只能放弃一些商店物品了QAQ

5. 代码

model:

sets:
vec4/1..4/: x, val,cost;
matrix(vec4,vec4): dat;
endsets

data:
dat = 13 100 0 0
	13 0 72 0 
	13 0 0 48
	49 13 12 9;
val = 6144 5540 5750 4350;
cost = 20 20 20 20;
enddata

min = @sum(vec4: x*cost);

@for(vec4(j): 
	@sum(vec4(i): x(i)*dat(i,j)) > val(j));

@for(vec4:@gin(x));
end