2023年度好题(2)
文章有点长,都是由本人一点一点写出来的,公式加载需要一段时间。
CF149D Coloring Brackets
思路
这是一道很好的区间 DP 题目。
我们可以设 \(f_{l, r, c1, c2}\) 表示在 \([l, r]\) 这一段头端染色 \(c1\),尾部染色 \(c2\) 可以获得方案数,\(c1, c2\) 可以为 \(0, 1, 2\),\(0\) 表示不染色,\(1, 2\) 是题目中规定的两种颜色。
对于 \(l, r\) 有三种情况:
- \(l, r\) 相邻,相邻的括号序列 \(()\) 可以染为 \(\{0, 1\}\{0, 2\}\{1, 0\}\{2, 0\}\)。
- 如果 \(match_l = r\) 且 \(l, r\) 不相邻,那么要先计算出 \(l + 1, r - 1\) 的染色方案,然后与 \(l, r\) 不冲突就可以相加。
- 如果 \(match_l \ne r\) 且 \(l, r\) 不相邻,那么分 \([l, match_l]\) 和 \([match_l + 1, r]\) 两段计算再合起来就可以啦。
是不是很简单?
代码
跑得飞快:

/*******************************
| Author: SunnyYuan
| Problem: Coloring Brackets
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF149D
| When: 2023-09-14 16:21:55
|
| Memory: 250 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 710, M = 3, MOD = 1000000007;
int f[N][N][M][M];
int n;
char s[N];
int match[N];
void init() {
stack<int> t;
for (int i = 1; i <= n; i++) {
if (s[i] == '(') t.push(i);
else {
match[t.top()] = i;
t.pop();
}
}
}
void dfs(int l, int r) {
if (r - l + 1 <= 2) {
for (int i = 0; i < M; i++) {
for (int j = 0; j < M; j++) {
if ((i == 0 && j == 0) || (i && j) || (i == j)) continue;
f[l][r][i][j] = 1;
}
}
return;
}
if (match[l] == r) {
dfs(l + 1, r - 1);
for (int i = 0; i < M; i++) {
for (int j = 0; j < M; j++) {
if ((i == 0 && j == 0) || (i && j) || (i == j)) continue;
for (int u = 0; u < M; u++) {
for (int v = 0; v < M; v++) {
if (i && u && (i == u)) continue;
if (v && j && (j == v)) continue;
f[l][r][i][j] = (f[l][r][i][j] + f[l + 1][r - 1][u][v]) % MOD;
}
}
}
}
}
else {
dfs(l, match[l]);
dfs(match[l] + 1, r);
for (int i = 0; i < M; i++) {
for (int j = 0; j < M; j++) {
for (int u = 0; u < M; u++) {
for (int v = 0; v < M; v++) {
if (j && u && (j == u)) continue;
f[l][r][i][v] = (f[l][r][i][v] + 1ll * f[l][match[l]][i][j] * f[match[l] + 1][r][u][v]) % MOD;
}
}
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> (s + 1);
n = strlen(s + 1);
init();
dfs(1, n);
int ans = 0;
for (int i = 0; i < M; i++)
for (int j = 0; j < M; j++)
ans = (ans + f[1][n][i][j]) % MOD;
cout << ans << '\n';
return 0;
}
P4822 [BJWC2012] 冻结
思路
非常水的一道题目,十分钟就水完了。
它只配是一个黄题
我们设 \(f_{i, j, k}\) 为从 \(i\) 到 \(j\) 使用 \(k\) 张卡所需要的最小时间。
然后就是在 Floyd 的算法基础上加入对卡片数量计算:
代码
/*******************************
| Author: SunnyYuan
| Problem: P4822 [BJWC2012] 冻结
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P4822
| When: 2023-09-14 17:25:34
|
| Memory: 125 MB
| Time: 3000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
int dis[N][N][N];
int n, m, f;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> f;
memset(dis, 0x3f, sizeof(dis));
for (int i = 1; i <= m; i++) {
int u, v, w;
cin >> u >> v >> w;
dis[u][v][0] = dis[v][u][0] = w; // 无重边
dis[u][v][1] = dis[v][u][1] = (w >> 1);
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
for (int l = 0; l <= k; l++)
for (int r = 0; l + r <= k; r++)
dis[i][j][l + r] = min(dis[i][j][l + r], dis[i][k][l] + dis[k][j][r]);
int ans = 0x3f3f3f3f;
for (int i = 1; i <= f; i++) ans = min(ans, dis[1][n][i]);
cout << ans << '\n';
return 0;
}
P6833 [Cnoi2020] 雷雨
思路
来水题解了
我们求出 \((1, a), (n, b), (n, c)\) 到每个点的最短路,记为 \(dis1, dis2, dis3\),然后枚举两束闪电的交点 \((i, j)\),那么最终的答案就是 \(\min\{dis1_{i, j} + dis2_{i, j} + dis3_{i, j} - 2s_{i, j}\}\)。
代码
/*******************************
| Author: SunnyYuan
| Problem: P6833 [Cnoi2020] 雷雨
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P6833
| When: 2023-09-14 20:35:33
|
| Memory: 128 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using PIII = pair<i64, pair<int, int> >;
const int N = 1010;
const i64 INF = 1e18;
int n, m, a, b, c;
i64 dis1[N][N];
i64 dis2[N][N];
i64 dis3[N][N];
bool vis[N][N];
int s[N][N];
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
void dijkstra(i64 dis[N][N], int x, int y) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dis[i][j] = INF;
vis[i][j] = false;
}
}
dis[x][y] = s[x][y];
priority_queue<PIII, vector<PIII>, greater<PIII> > q;
q.push({s[x][y], {x, y}});
while (q.size()) {
int x = q.top().second.first, y = q.top().second.second;
q.pop();
if (vis[x][y]) continue;
vis[x][y] = true;
for (int k = 0; k < 4; k++) {
int nx = x + dx[k], ny = y + dy[k];
if (dis[nx][ny] > dis[x][y] + s[nx][ny]) {
dis[nx][ny] = dis[x][y] + s[nx][ny];
q.push({dis[nx][ny], {nx, ny}});
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> a >> b >> c;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> s[i][j];
dijkstra(dis1, 1, a);
dijkstra(dis2, n, b);
dijkstra(dis3, n, c);
i64 len = INF;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
len = min(len, dis1[i][j] + dis2[i][j] + dis3[i][j] - s[i][j] * 2);
}
}
cout << len << '\n';
return 0;
}
P2700 逐个击破
思路
水题
我们使用 kruskal 算法的思想,不过这次是优先保留权值更大的边,这次判断的不是是否在一个环里面,而是是否边连接的两个部分都是有敌人的,如果都有敌人,那么不能连接这两条边,否则加入这条边,并且将两个部分合并。
代码
/*******************************
| Author: SunnyYuan
| Problem: P2700 逐个击破
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2700
| When: 2023-09-14 21:24:39
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010;
struct edge {
int u, v, w;
} e[N];
bool cmp(edge a, edge b) {
return a.w > b.w;
}
int fa[N], s[N];
int find(int x) {
if (x == fa[x]) return x;
return fa[x] = find(fa[x]);
}
int n, k;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k;
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= k; i++) {
int x;
cin >> x;
s[x] = true;
}
i64 ans = 0;
for (int i = 1; i < n; i++) cin >> e[i].u >> e[i].v >> e[i].w, ans += e[i].w;
sort(e + 1, e + n, cmp);
for (int i = 1; i < n; i++) {
int u = e[i].u, v = e[i].v, w = e[i].w;
int fx = find(u), fy = find(v);
if (s[fy] && s[fx]) continue;
ans -= w;
s[fy] |= s[fx];
fa[fx] = fy;
}
cout << ans << '\n';
return 0;
}
P3252 [JLOI2012] 树
思路
我们可以想到树上倍增的方法。
设 \(f_{i, k}\) 表示第 \(i\) 个点的 \(2^k\) 的父亲。
设 \(s_i\) 表示从根节点到 \(i\) 点的权值之和。
那么我们枚举点 \(u\),然后想找 \(LCA\) 一样进行试探,
知道找到一个 \(v\) 使得 \(a_u - a_v \le s\),如果 \(a_u - a_v\) 正好等于 \(s\),那么答案 \(ans + 1\),就可以了。
时间复杂度:\(O(n \log n)\)。
代码
/*******************************
| Author: SunnyYuan
| Problem: P3252 [JLOI2012] 树
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P3252
| When: 2023-09-14 22:50:44
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
struct edge {
int to, next;
} e[N];
int head[N], idx = 1;
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
}
int n, s;
int a[N], c[N];
int fa[N][20];
void dfs(int u, int f) {
fa[u][0] = f;
a[u] += a[f];
for (int i = head[u]; i; i = e[i].next) {
dfs(e[i].to, u);
}
}
void initfa() {
for (int j = 1; j < 20; j++)
for (int i = 1; i <= n; i++)
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> s;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
add(u, v);
}
dfs(1, 0);
initfa();
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (a[i] < s) continue;
else if (a[i] == s) {
cnt++;
continue;
}
int u = i;
for (int j = 19; j >= 0; j--) {
if (a[i] - a[fa[u][j]] <= s) {
u = fa[u][j];
}
}
if (a[i] - a[u] == s) cnt++;
}
cout << cnt << '\n';
return 0;
}
P1993 小 K 的农场
思路
有了差分约束系统,这个题就很简单了。
设 \(x_u\) 表示农场 \(u\) 种植的作物数量。
农场 \(a\) 比农场 \(b\) 至少多种植了 \(c\) 个单位的作物可以转化为 \(x_b - x_a \le -c\)。
农场 \(a\) 比农场 \(b\) 至多多种植了 \(c\) 个单位的作物可以转化为 \(x_a - x_b \le c\)。
农场 \(a\) 与农场 \(b\) 种植的作物数一样多可以转化为 \(x_a - x_b \le 0, x_b - x_a \le 0\)。
然后就是板子了,然后就没有然后了。
代码
/*******************************
| Author: SunnyYuan
| Problem: P1993 小 K 的农场
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P1993
| When: 2023-09-18 11:21:28
|
| Memory: 128 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 5010, M = 20010;
struct edge {
int to, next, w;
} e[M];
int head[N], idx = 1;
void add(int u, int v, int w) {
idx++, e[idx].to = v, e[idx].next = head[u], e[idx].w = w, head[u] = idx;
}
int n, m;
int dis[N];
int cnt[N];
bool st[N];
bool spfa(int u) {
memset(dis, 0x3f, sizeof(dis));
dis[u] = 0;
queue<int> q;
q.push(u);
st[u] = true;
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = head[t]; i; i = e[i].next) {
int to = e[i].to;
if (dis[to] > dis[t] + e[i].w) {
dis[to] = dis[t] + e[i].w;
cnt[to] = cnt[t] + 1;
if (cnt[to] >= n + 1) return false;
if (!st[to]) {
st[to] = true;
q.push(to);
}
}
}
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
int opt, a, b, c;
for (int i = 1; i <= n; i++) add(0, i, 0);
for (int i = 1; i <= m; i++) {
cin >> opt;
if (opt == 1) {
cin >> a >> b >> c;
// Xb - Xa <= -c
add(a, b, -c);
}
else if (opt == 2) {
cin >> a >> b >> c;
// Xa - Xb <= c
add(b, a, c);
}
else {
cin >> a >> b;
add(a, b, 0);
add(b, a, 0);
}
}
if (spfa(0)) cout << "Yes\n";
else cout << "No\n";
return 0;
}
P4926 [1007] 倍杀测量者
思路
这个紫题还算比较水。
众所周知,乘法可以 \(\log\) 以后转化为加法。
比如 \(a\times b \le c\) 可以转化为 \(\log a + \log b \le \log c\)。
回到题目,我们可以转化一下题意:
“选手 Y 只要成功 \(k - T\) 倍杀了选手 X”可以转化为 \(score_Y \ge (k - T) score_X\)。
“选手 Y 只要没有成功被选手 X \(k + T\) 倍杀”可以转化为 \(score_X < (k + T) score_Y\)。
我们现在对它们进行转化。
然后我们将从超级源点连向已知的分数,然后就是标准的差分约束系统,然后就没有然后了。
代码
/*******************************
| Author: SunnyYuan
| Problem: P4926 [1007] 倍杀测量者
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P4926
| When: 2023-09-18 11:34:51
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 5010;
const double eps = 1e-6, INF = 1e18;
struct edge {
int opt, to, next;
double w;
} e[M];
int head[N], idx = 1;
void add(int opt, int u, int v, double w) {
idx++, e[idx].opt = opt, e[idx].to = v, e[idx].next = head[u], e[idx].w = w, head[u] = idx;
}
int n, s, t; // n: 机房人数 s: 立下的 flag 总数 t: 已知分数人数
int cmp(double a, double b) {
if (fabs(a - b) < eps) return 0;
if (a < b) return -1;
return 1;
}
double dis[N];
int cnt[N];
bool st[N];
bool spfa(int s, double T) {
queue<int> q;
q.push(s);
for (int i = 0; i <= n; i++) {
dis[i] = -INF;
cnt[i] = 0;
st[i] = false;
}
dis[s] = 0;
st[s] = true;
while (q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for (int i = head[t]; i; i = e[i].next) {
int to = e[i].to;
double w = log2(e[i].w);
if (e[i].opt == 1) w = log2(e[i].w - T);
else if (e[i].opt == 2) w = -log2(e[i].w + T);
if (cmp(dis[to], dis[t] + w) == -1) {
dis[to] = dis[t] + w;
cnt[to] = cnt[t] + 1;
if (cnt[to] >= n + 1) return false;
if (!st[to]) {
st[to] = true;
q.push(to);
}
}
}
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> s >> t;
int opt, a, b;
double k;
for (int i = 1; i <= s; i++) {
cin >> opt >> a >> b >> k;
add(opt, b, a, k);
}
for (int i = 1; i <= t; i++) {
int x;
double v;
cin >> x >> v;
add(-1, 0, x, v);
add(-1, x, 0, 1 / v);
}
if (spfa(0, 0)) {
cout << "-1\n";
return 0;
}
double l = eps, r = 1e18, mid = 0.0;
while (cmp(l, r)) {
mid = (l + r) / 2.0;
if (spfa(0, mid)) r = mid;
else l = mid;
}
cout << setprecision(10) << fixed << l << '\n';
return 0;
}
[ARC165A] Sum equals LCM
思路
cn_ryh 老师爆切了这个经典题,然后 Let me try try。
我们发现在 \(a, b \ge 2\) 时,\(a + b \le a \times b\)。
所以这个题就是看 \(x\) 能不能分解质因数且质因数个数大于等于 \(2\) 个就可以了,如果这些质因数全部加起来 \(\le x\),那么就补 \(1\),因为 \(1\) 并不影响 \(\text{LCM}\)。
代码
#include <bits/stdc++.h>
using namespace std;
void solve() {
int x;
cin >> x;
set<int> s;
for (int i = 2; i * i <= x; i++) {
if (x % i == 0) {
s.insert(i);
}
while (x % i == 0) x /= i;
}
if (x > 1) s.insert(x);
cout << (s.size() >= 2 ? "Yes\n" : "No\n");
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
SP5973 SELTEAM - Selecting Teams
思路
我们对选择 \(1 \sim k\) 个人进行枚举,然后发现:
那这个式子是什么意思呢?我们从 \(1\) 枚举到 \(k\) 表示我们选择 \(i\) 个人作为一个球队,对于一个球队,我们要选择一个队长,选队长有 \(i\) 种选择,剩下 \(i - 1\) 个人可以选择也可以不选择,所以总共有 \(2^{i - 1}\) 种选择,这里利用了乘法原理和加法原理。
然后我们发现模数 \(8388608 = 2^{23}\),所以对于 \(i > 23\),\(C_n^i\cdot i\cdot 2^{i - 1}\) 的余数始终为 \(0\),所以我们至多计算 \(23\) 次,即 \(i\) 循环到 \(\min(23, k)\) 即可。
upd 9/19/2023
那怎么求组合数呢?
设 \(f_{i, j}\) 表示 \(C_i^j\),我们发现
\(f_{i - 1, j - 1} + f_{i - 1, j}\) 表示第 \(i\) 个要选择时,那么选择到第 \(i - 1\) 个时已经选择了 \(j - 1\) 个,否则如果不选第 \(i\) 个时,选到第 \(i - 1\) 个时已经选择了 \(j\) 个,不会增多了。
代码
#include <bits/stdc++.h>
using namespace std;
const int mod = 8388608, N = 100010, S = 30;
int c[N][S];
void init() {
c[0][0] = 1;
for (int i = 1; i < N; i++) {
c[i][0] = 1;
for (int j = 1; j <= min(S - 1, i); j++) {
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
}
}
}
void solve() {
int n, k, ans = 0;
cin >> n >> k;
for (int i = 1; i <= min(k, 23); i++) {
ans = (ans + (1ll * c[n][i] * i * (1ll << (i - 1))) % mod) % mod;
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
int T;
cin >> T;
while (T--) solve();
return 0;
}
P4180 [BJWC2010] 严格次小生成树
代码
这道紫题很经典。
我们可以先用 Prim 算法或者 Kruskal 算法求出最小生成树。
我们要求严格次小生成树,那么可以想到要将一条边 \((u, v)\) 加入生成树,需要在最小生成树上的路径 \(u\rightarrow v\) 上选择一条边然后删掉,再加上 \((u, v)\) 这条边,这样才能保证它还是一棵树。
删掉的那条边可以是 \(u\rightarrow v\) 这条路径上边权最大的一条边,但是如果最大值等于要加的边的权值,那么就做不到“严格次小生成树”,它还是个最小生成树,所以还要记录一个次大值,用次大值来替换。
维护树上路径的权值最大值和次大值可以使用倍增 LCA 来求解。
然后最大值和次大值的维护我用的 set(简单好用),然后就没有然后了。
思路
/*******************************
| Author: SunnyYuan
| Problem: P4180 [BJWC2010] 严格次小生成树
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P4180
| When: 2023-09-19 10:42:55
|
| Memory: 500 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using PII = pair<i64, i64>;
const int N = 100010, M = 300010;
const i64 INF = 1e18;
struct edge {
int u, v, w;
} e[M];
vector<PII> graph[N]; // 生成树
int n, m;
int fa[N];
i64 mintree; // 最小生成树
int find(int x) {
if (x == fa[x]) return x;
return fa[x] = find(fa[x]);
}
int s[N][25];
i64 w[N][25];
i64 c[N][25];
int dep[N];
void dfs(int u, int fa) {
s[u][0] = fa;
dep[u] = dep[fa] + 1;
for (auto to : graph[u]) {
if (to.first == fa) continue;
dfs(to.first, u);
w[to.first][0] = to.second;
c[to.first][0] = -INF;
}
}
set<i64> p;
PII merge(i64 a, i64 b, i64 c, i64 d) {
p.clear();
p.insert(-a), p.insert(-b), p.insert(-c), p.insert(-d);
auto begin = p.begin();
return {-(*begin), -(*(++begin))};
}
void initlca() {
for (int j = 1; j < 25; j++) {
for (int i = 1; i <= n; i++) {
auto ans = merge(w[i][j - 1], c[i][j - 1], w[s[i][j - 1]][j - 1], c[s[i][j - 1]][j - 1]);
w[i][j] = ans.first, c[i][j] = ans.second;
s[i][j] = s[s[i][j - 1]][j - 1];
}
}
}
PII query(int l, int r) {
PII ans = {-INF, -INF};
if (dep[l] < dep[r]) swap(l, r);
for (int j = 24; j >= 0; j--) {
if (dep[s[l][j]] >= dep[r]) {
ans = merge(ans.first, ans.second, w[l][j], c[l][j]);
l = s[l][j];
}
}
if (l == r) return ans;
for (int j = 24; j >= 0; j--) {
if (s[l][j] != s[r][j]) {
ans = merge(ans.first, ans.second, w[l][j], c[l][j]);
ans = merge(ans.first, ans.second, w[r][j], c[r][j]);
l = s[l][j], r = s[r][j];
}
}
ans = merge(ans.first, ans.second, w[l][0], c[l][0]);
ans = merge(ans.first, ans.second, w[r][0], c[l][0]);
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= m; i++) cin >> e[i].u >> e[i].v >> e[i].w;
sort(e + 1, e + m + 1, [](const edge a, const edge b) { return a.w < b.w; });
for (int i = 1; i <= m; i++) {
int u = e[i].u, v = e[i].v, w = e[i].w;
int fx = find(u), fy = find(v);
if (fx == fy) continue;
graph[u].push_back({v, w});
graph[v].push_back({u, w});
fa[fx] = fy;
mintree += e[i].w;
}
w[1][0] = c[1][0] = w[0][0] = c[0][0] = -INF;
dfs(1, 0);
initlca();
i64 ans = INF;
for (int i = 1; i <= m; i++) {
int u = e[i].u, v = e[i].v;
auto getmax = query(u, v);
i64 maxx = (e[i].w == getmax.first ? getmax.second : getmax.first);
ans = min(ans, mintree - maxx + e[i].w);
}
cout << ans << '\n';
return 0;
}
P1725 琪露诺
思路
容易发现
然后我们暴力统计就可以获得 60 分的好成绩,开个 O2 直接过了。
但是我们是严谨的 OIer,一定要保证时间复杂度是正确的。
这个题显然可以用单调队列进行优化。
然后队列从后往前从大到小维护 \(f\),\(f_i = f_{\text{队首}} + a_i\),如果 \(i \ge l\) 就将 \(f_{i - l}\) 放入单调队列,然后就没有然后了。
代码
/*******************************
| Author: SunnyYuan
| Problem: P1725 琪露诺
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P1725
| When: 2023-09-19 16:29:00
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 300010, INF = 0x3f3f3f3f;
int n, l, r;
int q[N];
i64 f[N], a[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> l >> r;
for (int i = 0; i <= n; i++) cin >> a[i];
for (int i = 0; i < n + r; i++) f[i] = -INF;
f[0] = 0;
int hh = 0, tt = -1;
for (int i = 0; i < n + r; i++) {
// [i - r, i - l]
while (hh <= tt && q[hh] < i - r) hh++;
if (i >= l) {
while (hh <= tt && f[q[tt]] <= f[i - l]) tt--;
q[++tt] = i - l;
f[i] = f[q[hh]] + a[i];
}
}
i64 ans = -INF;
for (int i = n; i < n + r; i++) ans = max(ans, f[i]);
cout << ans << '\n';
return 0;
}
P2340 [USACO03FALL] Cow Exhibition G
思路
这个题目不同于普通的 01 背包。
设 \(f_{i, j}\) 表示考虑到第 \(i\) 个物品,智商为 \(j\) 可以获得的最高情商为多少。
假设 \(a_i\) 表示智商,\(b_i\) 表示情商。
\(f_{i, j} = \max(f_{i - 1, j}, f_{i - 1, j - a_i} + b_i)\)
因为空间不够,所以只能将二维降为一维。
很标准的递推式:\(f_j = \max(f_j, f_{j - a_i} + b_i)\)。
重点来了,如果牛 \(i\) 的智商 \(a_i < 0\) 要正着枚举,否则 \(a_i \ge 0\),就可以像普通的 01 背包一样倒着枚举。
答案就是 \(\max\{i + f_i\}\),当然要保证 \(f_i > 0\) 才能算!
还有,智商的和也有可能为负数,所以先将指针往后移 500000 位,这样 f[-1], f[-2], f[-3] 也都可以访问了。
代码
/*******************************
| Author: SunnyYuan
| Problem: P2340 [USACO03FALL] Cow Exhibition G
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2340
| When: 2023-09-19 16:55:07
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 410, M = 500010;
int n;
int dp[M * 2];
int *f = dp + 500000;
int a[N], b[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];
memset(dp, -0x3f, sizeof(dp));
f[0] = 0;
for (int i = 1; i <= n; i++) {
if (a[i] > 0) for (int j = 400000; j >= -400000; j--) f[j] = max(f[j], f[j - a[i]] + b[i]);
else for (int j = -400000; j <= 400000; j++) f[j] = max(f[j], f[j - a[i]] + b[i]);
}
int ans = 0;
for (int i = 0; i <= 400000; i++) if (f[i] >= 0) ans = max(ans, i + f[i]);
cout << ans << '\n';
return 0;
}
P4552 [Poetize6] IncDec Sequence
思路
我们先求一个差分数组 \(c_i = a_i - a_{i - 1}\),然后发现正负可以抵消,抵消完剩下的可以跟第一个元素 \(c_1\) 对着干,直到对于 \(i > 1\) 的部分,\(c_i\) 都等于 \(0\)。那么答案就是 \(\max(sum1, sum2)\),\(sum1\) 表示在 \(c\) 数组中所有非负数之和,\(sum2\) 表示在 \(c\) 数组中所有负数的绝对值之和。
对于第二问,我们发现我们可以跟第一个元素 \(c_1\) 抵消,也可以跟 \(c_{n + 1}\) 抵消,所以总共有 \(|sum1 - sum2| + 1\) 种方案。
然后我觉得我解释得像 1 + 1 = 3 一样简单,不适合作为题解,然后就没有然后了。
代码
/*******************************
| Author: SunnyYuan
| Problem: P4552 [Poetize6] IncDec Sequence
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P4552
| When: 2023-09-19 21:41:50
|
| Memory: 128 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010;
int n;
i64 a[N];
i64 ans1, ans2;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = n; i >= 1; i--) a[i] -= a[i - 1];// 求差分
for (int i = 2; i <= n; i++) { // 求正负之和
if (a[i] > 0) ans1 += a[i];
else ans2 += -a[i];
}
cout << max(ans1, ans2) << '\n' << llabs(ans1 - ans2) + 1 << '\n';
return 0;
}
CF1870C Colorful Table 题解
思路
当一个数字 \(x\) 碰上了比它更大的数字 \(y\) 才有可能在 \(\min(x, y)\) 被输出。
所以这道题的思路就是对于 \(k\),找到最小的 \(j\) 使得 \(a_j \ge k\),找到最大的 \(p\) 使得 \(a_p \ge k\),一定有 \(\min(a_j, k) = k, \min(a_p, k) = k\),反过来也一样,\(\min(k, a_j) = k, \min(k, a_p) = k\),所以对于 \(k\) 的影响力也就 \(j\sim p\) 行和 \(j \sim p\) 列,所以必须拿长宽都为 \(p - j + 1\) 的正方形覆盖,所以答案为长宽之和为 \(2(p - j + 1)\)(题目要求的)。
代码
代码中 first[i] 表示数字 \(i\) 第一次出现在数组中的位置;last[i] 表示数字 \(i\) 最后一次出现在数组中的位置;max_last[i] 表示最大的坐标 \(p\) 使得 \(a_p \ge i\);min_first[i] 表示最小的坐标 \(j\) 使得 \(a_j \ge i\)。
还有,一定要注意,如果一个数字没有出现过,那么一定不要计算进去啊!
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, INF = 0x3f3f3f3f;
int n, k;
int a[N];
int first[N], last[N];
int max_last[N];
int min_first[N]; // 数组的意思都在上面写过了
void solve() {
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
if (!first[a[i]]) first[a[i]] = i;
last[a[i]] = i;
}
for (int i = 0; i <= k + 1; i++) min_first[i] = INF, max_last[i] = -INF;
for (int i = k; i >= 1; i--) {
if (last[i]) max_last[i] = max(max_last[i + 1], last[i]);
else max_last[i] = max_last[i + 1]; // 如果一个数字没有出现过,那么一定不要计算进去
}
for (int i = k; i >= 1; i--) {
if (first[i]) min_first[i] = min(min_first[i + 1], first[i]);
else min_first[i] = min_first[i + 1]; // 如果一个数字没有出现过,那么一定不要计算进去
}
for (int i = 1; i <= k; i++) {
if (!first[i]) {
cout << "0 ";
continue;
}
int p1 = min_first[i], p2 = max_last[i];
cout << 2 * (p2 - p1 + 1) << ' ';
}
cout << '\n';
for (int i = 0; i <= k; i++) first[i] = last[i] = max_last[i] = min_first[i] = 0; // 清空
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P3469 [POI2008] BLO-Blockade
前言
思路
实际上就是我们要找出割点,然后算出被割点分成的几部分两两相乘的和即可。注意删除一个点的所有边还可以贡献 \(2(n - 1)\) 个组合。
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010, M = 1000010;
struct edge {
int to, next;
} e[M];
int head[N], idx = 1;
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
}
int n, m;
int dfn[N], low[N], tot;
int sz[N], t[N];
i64 res[N];
bool cut[N];
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++tot;
int ch = 0;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (!dfn[to]) {
ch++;
tarjan(to, u);
low[u] = min(low[u], low[to]);
if ((low[to] >= dfn[u] && u != fa) || (ch >= 2 && u == fa)) {
cut[u] = true;
res[u] += 1ll * sz[to] * t[u];
t[u] += sz[to];
}
sz[u] += sz[to];
}
else if (to != fa) low[u] = min(low[u], dfn[to]);
}
sz[u]++;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
int u, v;
for (int i = 1; i <= m; i++) {
cin >> u >> v;
add(u, v), add(v, u);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) tarjan(i, i);
}
for (int i = 1; i <= n; i++) {
if (cut[i]) cout << 2 * (n - 1 + res[i] + 1ll * t[i] * (n - t[i] - 1)) << '\n';
else cout << 2 * (n - 1) << '\n';
}
return 0;
}
P1155 [NOIP2008 提高组] 双栈排序
思路
刚拿到题目非常迷茫,然后看了一眼题解。
我们可以发现,当 \(a_k < a_i < a_j\) 时,\(i\) 要在 \(j\) 前面弹出,\(k\) 又要在 \(a_i\) 和 \(a_j\) 之前弹出,所以是矛盾的。
所以我们可以建立一个二分图,从左到右连接矛盾的 \(i, j\),然后根据染上的颜色进行判断,进行入栈和出栈操作。
然后我们发现 \(d, a\) 和 \(c, b\) 这两个完全无关的操作放在一起会导致字典序变大,所以当遇到 \(d, a\) 和 \(c, b\) 就要调换它们的顺序。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
vector<int> e[N];
int n, a[N], minn[N];
int color[N];
bool dfs(int u, int c) {
color[u] = c;
for (int to : e[u]) {
if (!color[to]) {
if (!dfs(to, 3 - c)) {
return false;
}
}
else {
if (color[to] != 3 - c) {
return false;
}
}
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
minn[n + 1] = 0x3f3f3f3f;
for (int i = n; i >= 1; i--) minn[i] = min(minn[i + 1], a[i]);
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j < n; j++) {
if (minn[j + 1] < a[i] && a[i] < a[j]) {
e[a[i]].push_back(a[j]);
e[a[j]].push_back(a[i]);
}
}
}
for (int i = 1; i <= n; i++) {
if (!color[a[i]]) {
if (!dfs(a[i], 1)) {
cout << "0\n";
return 0;
}
}
}
stack<int> s1, s2;
string s;
int tmp = 1;
for (int i = 1; i <= n; i++) {
if (color[a[i]] == 1) {
s.push_back('a');
s1.push(a[i]);
}
else {
s.push_back('c');
s2.push(a[i]);
}
while ((s1.size() && s1.top() == tmp) || (s2.size() && s2.top() == tmp)) {
if (s1.size() && s1.top() == tmp) {
s1.pop();
s.push_back('b');
}
else {
s2.pop();
s.push_back('d');
}
tmp++;
}
}
for (int i = 0; i < s.size() - 1; i++) {
if (s[i] == 'd' && s[i + 1] == 'a') {
swap(s[i], s[i + 1]);
}
if (s[i] == 'c' && s[i + 1] == 'b') {
swap(s[i], s[i + 1]);
}
}
for (auto x : s) cout << x << ' ';
return 0;
}
P1433 吃奶酪
思路
我们发现用 dfs 就可以拿到 90 分的好成绩。
然后,我们发现 \(n\le 15\),所以我们可以想到用状压。
设 \(f_{i, j}\) 表示到第 \(i\) 号点,状态为 \(j\),如果 \(j\) 的第 \(k\) 位,等于 \(1\),就是已经走过了 \(k\) 点。
那可以枚举从哪里来,假设从点 \(k\) 来,看点 \(k\) 能不能更新答案:
但是一定要注意,状态 \(j\) 的第 \(k\) 位,一定要是 \(1\),第 \(i\) 位,也必须是 \(1\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
double f[N][1 << N];
struct point {
double x, y;
} p[N];
double dis(int x, int y) {
return sqrt((p[x].x - p[y].x) * (p[x].x - p[y].x) + (p[x].y - p[y].y) * (p[x].y - p[y].y));
}
int n;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> p[i].x >> p[i].y;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= (1 << n + 1); j++) {
f[i][j] = 1e18;
}
}
f[0][1] = 0;
for (int j = 0; j < (1 << n + 1); j++) {
for (int i = 0; i <= n; i++) {
if (j >> i & 1) {
for (int k = 1; k <= n; k++) {
if (j >> k & 1) {
f[k][j] = min(f[k][j], f[i][j - (1 << k)] + dis(i, k));
// cout << k << ' ' << j << ' ' << i << ' ' << (j - (1 << i)) << endl;
}
}
}
}
}
double ans = 1e18;
for (int i = 1; i <= n; i++) {
ans = min(ans, f[i][(1 << (n + 1)) - 1]);
}
cout << setprecision(2) << fixed << ans << '\n';
return 0;
}
POJ3134. Power Calculus
题意
给你一个数字 \(n\),设 \(x\) 初始值为 \(1\),问每次可以加上或减去一个前面出现过的 \(x\),最少几次可以到达 \(n\)。\(x\) 在操作中必须为正数。
思路
这个题目,我们可以想到在原来暴力的基础上进行优化,即使用 IDA*。
不会 IDA* 的可以看看我的博客。
现在想想怎么写 \(h()\) 函数呢?如果从当前 \(x\) 开始,不断加上最大的可以用的数字(也就是 \(x\)),那么相当于每次将 \(x = x + x\),那么每次 \(x\) 的值都可以变成 \(2x\),那么假如现在还能操作 \(cnt\) 次,如果 \(x \cdot 2 ^ {cnt} < n\),那么在怎么样也到达不了目标,直接返回即可。
代码
/*******************************
| Author: SunnyYuan
| Problem: Power Calculus
| Contest: Virtual Judge - POJ
| URL: https://vjudge.net/problem/POJ-3134
| When: 2023-09-27 14:55:12
|
| Memory: 64 MB
| Time: 5000 ms
*******************************/
#include <iostream>
using namespace std;
int n, depth, x;
int use[110], c;
bool dfs(int dep) {
if (dep > depth) return false;
if (x == n) return true;
if (x << (depth - dep)< n) return false;
use[++c] = x;
for (int i = 1; i <= c; i++) {
int y = use[i];
x += y;
if (dfs(dep + 1)) return true;
x -= y;
if (x > y) {
x -= y;
if (dfs(dep + 1)) return true;
x += y;
}
}
c--;
return false;
}
int main() {
while (cin >> n, n) {
x = 1;
c = 0;
for (depth = 0; ; depth++) {
if (dfs(0)) {
cout << depth << '\n';
break;
}
}
}
return 0;
}
UVA 1343 旋转游戏
思路
首先是暴力,暴力每次要进行什么操作,然后我们可以使用 IDA* 进行优化。
不会 IDA* 的,可以参考我的博客。
那怎么写 \(h()\) 函数呢?因为只有 \(1, 2, 3\) 三个数字,那么我们对 \(3\) 个数字分别进行讨论,发现对于一个数字 \(x\),想要让中间都是 \(x\),那么我们就算出中间有多少个点不是 \(x\) 的数量 \(c\),那么这些点至少要挪动 \(1\) 个位置,所以总共至少要 \(c\) 次操作才能完成。最后再在 \(1, 2, 3\) 中找出一个最少次数作为 \(h()\) 函数的值返回。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 7, INF = 0x3f3f3f3f;
int a[N][N];
int depth;
string ans;
bool check() {
int x = INF;
for (int i = 2; i <= 4; i++) {
for (int j = 2; j <= 4; j++) {
if (i == 3 && j == 3) continue;
if (x == INF) x = a[i][j];
if (a[i][j] != x) return false;
}
}
return true;
}
void gonxt_line(int line) {
int x = a[line][6];
for (int i = 6; i > 0; i--) a[line][i] = a[line][i - 1];
a[line][0] = x;
}
void gonxt_col(int col) {
int x = a[6][col];
for (int i = 6; i > 0; i--) a[i][col] = a[i - 1][col];
a[0][col] = x;
}
void gopre_line(int line) {
int x = a[line][0];
for (int i = 0; i < 6; i++) a[line][i] = a[line][i + 1];
a[line][6] = x;
}
void gopre_col(int col) {
int x = a[0][col];
for (int i = 0; i < 6; i++) a[i][col] = a[i + 1][col];
a[6][col] = x;
}
void process(char opt) {
if (opt == 'A') gopre_col(2);
if (opt == 'F') gonxt_col(2);
if (opt == 'B') gopre_col(4);
if (opt == 'E') gonxt_col(4);
if (opt == 'H') gopre_line(2);
if (opt == 'C') gonxt_line(2);
if (opt == 'G') gopre_line(4);
if (opt == 'D') gonxt_line(4);
}
char calcback(char opt) {
char cur = -1;
if (opt == 'A') cur = 'F';
if (opt == 'B') cur = 'E';
if (opt == 'C') cur = 'H';
if (opt == 'D') cur = 'G';
if (opt == 'E') cur = 'B';
if (opt == 'F') cur = 'A';
if (opt == 'G') cur = 'D';
if (opt == 'H') cur = 'C';
return cur;
}
void goback(char opt) {
process(calcback(opt));
}
int h() {
int cnt[4] = {0, 0, 0, 0};
for (int i = 2; i <= 4; i++) {
for (int j = 2; j <= 4; j++) {
if (i == 3 && j == 3) continue;
cnt[a[i][j]]++;
}
}
int ans = INF;
for (int i = 1; i <= 3; i++) ans = min(ans, 8 - cnt[i]);
return ans;
}
bool dfs(char last, int dep) {
if (dep > depth) return false;
if (check()) return true;
if (dep + h() > depth) return false;
// g[a] = true;
for (int i = 0; i < 8; i++) {
char opt = 'A' + i;
if (calcback(opt) == last) continue;
process(opt);
ans.push_back(opt);
if (dfs(opt, dep + 1)) return true;
ans.pop_back();
goback(opt);
}
return false;
}
bool solve() {
int x;
cin >> x;
if (!x) return false; // end
a[0][2] = x;
cin >> a[0][4];
for (int i = 1; i < N; i++) {
if (i == 0 || i == 1 || i == 3 || i == 5 || i == 6) cin >> a[i][2] >> a[i][4];
else for (int j = 0; j < N; j++) cin >> a[i][j];
}
ans.clear();
for (depth = 0; ; depth++) {
if (dfs(-1, 0)) {
assert(ans.size() == depth);
if (!depth) cout << "No moves needed\n" << a[2][2] << '\n';
else cout << ans << '\n' << a[2][2] << '\n';
return true;
}
}
}
int main() {
// freopen("test.in", "r", stdin);
ios::sync_with_stdio(false);
cin.tie(nullptr);
while (solve());
return 0;
}
P2346 四子连棋
思路
思路就是算先手是黑的和白的答案再取 \(\min\)。
那怎么计算答案呢?
我们使用 dfs 枚举下一次走哪一步。
然后就是使用 IDA* 优化,不会的看我博客。
那怎么写 \(h()\) 函数呢?
我们计算一行,一列或一条对角线是黑或白的最小步骤,然后再取一个 \(\min\)。
那怎么计算最小步骤呢?如果一个颜色不在一条直线上,那么至少需要 \(1\) 步才能归位,所以就是最小步骤就是不是某个颜色的格子数量。
代码
代码不长,就 200 多行。
/*******************************
| Author: SunnyYuan
| Problem: P2346 四子连棋
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2346
| When: 2023-09-27 15:54:52
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
using PII = pair<int, int>;
const int N = 4;
char s[N][N];
char g[N][N];
int depth;
int h() {
// line
int c1 = 0, c2 = 0;
for (int i = 0; i < N; i++) {
int p1 = 0, p2 = 0;
for (int j = 0; j < N; j++) {
if (s[i][j] == 'B') p1++;
else if(s[i][j] == 'W') p2++;
else p1 = p2 = -0x3f3f3f3f;
}
c1 = max(c1, p1), c2 = max(c2, p2);
}
// col
for (int j = 0; j < N; j++) {
int p1 = 0, p2 = 0;
for (int i = 0; i < N; i++) {
if (s[i][j] == 'B') p1++;
else if (s[i][j] == 'W') p2++;
else p1 = p2 = -0x3f3f3f3f;
}
c1 = max(c1, p1), c2 = max(c2, p2);
}
// djx
int p1 = 0, p2 = 0;
for (int i = 0; i < N; i++) {
if (s[i][i] == 'B') p1++;
else if (s[i][i] == 'W') p2++;
else p1 = p2 = -0x3f3f3f3f;
}
c1 = max(c1, p1), c2 = max(c2, p2);
p1 = p2 = 0;
for (int i = 0; i < N; i++) {
if (s[i][3 - i] == 'B') p1++;
else if (s[i][3 - i] == 'W') p2++;
else p1 = p2 = -0x3f3f3f3f;
}
c1 = max(c1, p1), c2 = max(c2, p2);
return min(4 - c1, 4 - c2);
}
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
bool dfs1(int dep) {
if (dep > depth) return false;
if (!h()) return true;
if (dep + h() > depth) return false;
PII s1 = {-1, -1}, s2 = {-1, -1};
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
if (s[i][j] == 'O') {
if (s1.x == -1) s1 = {i, j};
else s2 = {i, j};
}
if (dep & 1) { // black
for (int i = 0; i < 4; i++) {
int nx = s1.x + dx[i], ny = s1.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'B') {
swap(s[s1.x][s1.y], s[nx][ny]);
if(dfs1(dep + 1)) return true;
swap(s[s1.x][s1.y], s[nx][ny]);
}
}
for (int i = 0; i < 4; i++) {
int nx = s2.x + dx[i], ny = s2.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'B') {
swap(s[s2.x][s2.y], s[nx][ny]);
if(dfs1(dep + 1)) return true;
swap(s[s2.x][s2.y], s[nx][ny]);
}
}
}
else {
for (int i = 0; i < 4; i++) {
int nx = s1.x + dx[i], ny = s1.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'W') {
swap(s[s1.x][s1.y], s[nx][ny]);
if(dfs1(dep + 1)) return true;
swap(s[s1.x][s1.y], s[nx][ny]);
}
}
for (int i = 0; i < 4; i++) {
int nx = s2.x + dx[i], ny = s2.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'W') {
swap(s[s2.x][s2.y], s[nx][ny]);
if(dfs1(dep + 1)) return true;
swap(s[s2.x][s2.y], s[nx][ny]);
}
}
}
return false;
}
bool dfs2(int dep) {
if (dep > depth) return false;
if (!h()) return true;
if (dep + h() > depth) return false;
PII s1 = {-1, -1}, s2 = {-1, -1};
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
if (s[i][j] == 'O') {
if (s1.x == -1) s1 = {i, j};
else s2 = {i, j};
}
if (!(dep & 1)) { // black
for (int i = 0; i < 4; i++) {
int nx = s1.x + dx[i], ny = s1.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'B') {
swap(s[s1.x][s1.y], s[nx][ny]);
if(dfs2(dep + 1)) return true;
swap(s[s1.x][s1.y], s[nx][ny]);
}
}
for (int i = 0; i < 4; i++) {
int nx = s2.x + dx[i], ny = s2.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'B') {
swap(s[s2.x][s2.y], s[nx][ny]);
if(dfs2(dep + 1)) return true;
swap(s[s2.x][s2.y], s[nx][ny]);
}
}
}
else {
for (int i = 0; i < 4; i++) {
int nx = s1.x + dx[i], ny = s1.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'W') {
swap(s[s1.x][s1.y], s[nx][ny]);
if(dfs2(dep + 1)) return true;
swap(s[s1.x][s1.y], s[nx][ny]);
}
}
for (int i = 0; i < 4; i++) {
int nx = s2.x + dx[i], ny = s2.y + dy[i];
if (nx < 0 || ny < 0 || nx > 3 || ny > 3) continue;
if (s[nx][ny] == 'W') {
swap(s[s2.x][s2.y], s[nx][ny]);
if(dfs2(dep + 1)) return true;
swap(s[s2.x][s2.y], s[nx][ny]);
}
}
}
return false;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
cin >> s[i][j];
g[i][j] = s[i][j];
}
}
int ans = 0x3f3f3f3f;
for (depth = 0; ; depth++) {
if (dfs1(0)) {
ans = min(ans, depth);
break;
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
s[i][j] = g[i][j];
}
}
for (depth = 0; ; depth++) {
if (dfs2(0)) {
ans = min(ans, depth);
break;
}
}
cout << ans << '\n';
return 0;
}
P2324 [SCOI2005] 骑士精神
思路
这个蒟蒻把颜色认反了,然后调试了 30 分钟。
可以想到用 dfs,每次暴力枚举将哪个棋子放到空格。
然后我们可以用 IDA* ,不知道的,可以参考参考我的博客。
我们来想一想怎么写 \(h()\) 函数,我们发现一个点如果与目标状态的点的颜色不一致,那么一定会花费至少一步才能到达目标,那么 \(h()\) 函数返回的就是所有不一致的点的数量 \(-1\),为什么要 \(-1\) 呢?
- 因为如果其他点都确定了,那个点也确定了。
- \(h()\) 函数可以放的松一点,否则容易 WA。
代码
/*******************************
| Author: SunnyYuan
| Problem: P2324 [SCOI2005] 骑士精神
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2324
| When: 2023-09-27 16:53:21
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using PII = pair<int, int>;
const int N = 5;
char s[N][N];
char des[N][N] = {
'1', '1', '1', '1', '1',
'0', '1', '1', '1', '1',
'0', '0', '*', '1', '1',
'0', '0', '0', '0', '1',
'0', '0', '0', '0', '0',
};
int dx[8] = {-2, -2, -1, 1, 2, 2, 1, -1};
int dy[8] = {1, -1, -2, -2, -1, 1, 2, 2};
int depth;
int h() {
int cnt = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (s[i][j] != des[i][j]) {
cnt++;
}
}
}
return cnt;
}
bool dfs(int last_x, int last_y, int dep) {
if (dep > depth) return false;
if (!h()) return true;
if (dep + h() - 1 > depth) return false;
int x = -1, y = -1;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (s[i][j] == '*') {
x = i, y = j;
}
}
if (x != -1) break;
}
for (int i = 0; i < 8; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx < 0 || ny < 0 || nx > 4 || ny > 4) continue;
if (nx == last_x && ny == last_y) continue;
swap(s[x][y], s[nx][ny]);
if (dfs(x, y, dep + 1)) return true;
swap(s[x][y], s[nx][ny]);
}
return false;
}
void solve() {
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
cin >> s[i][j];
for (depth = 0; depth <= 15; depth++) {
if (dfs(-1, -1, 0)) {
cout << depth << '\n';
return;
}
}
cout << "-1\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P1326 足球
思路
求最大得分
我们可以先赢 \(\min(S, n - 1)\) 场比分为 \(1 : 0\) 的比赛,然后将输球全部累计到一场比赛中,即比分为 \(0 : T\) 的比赛,剩下的算平局。如果 \(T = 0\),那么 \(0 : T\) 也不算输,那么平局就多了一局。
求最小得分
我们可以让一场比赛赢,其他的比赛输或者平局或者让全部的比赛赢。
只有 \(S \le T\) 才能让全部的比赛赢,而让一场比赛赢,其他的比赛输或者平局的则对 \(S, T\) 没有限制。
代码
/*******************************
| Author: SunnyYuan
| Problem: P1326 足球
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P1326
| When: 2023-09-30 08:27:48
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
i64 s, t, n;
void solve() {
i64 maxx = 0, minn = 0x3f3f3f3f3f3f3f3f;
if (s < n) maxx = 3 * s + (n - s - (t != 0));
else maxx = 3 * (n - 1) + ((s - (n - 1)) >= t ? ((s - (n - 1)) == t ? 1 : 3) : 0);
minn = 3 + n - 1 - min(n - 1, t);
if (s <= t) minn = min(minn, n - min(n, (t - s)));
cout << maxx << ' ' << minn << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
while (cin >> s >> t >> n) solve();
return 0;
}
参考文献
P2149 [SDOI2009] Elaxia的路线
思路
这道蓝题很有意思。
我们可以跑四次最短路求出答案。
首先我们先求出源点为 \(x_1, x_2\) 的单源最短路径 \(dis_1, dis_2\),\(x_1, x_2\) 为第一个人的起点与终点。
假设一条边 \((u, v)\) 满足 \({dis_1}_u + w_{u, v} + {dis_2}_v = {dis_1}_{x_2}\),就证明有一条从 \(x_1\) 到 \(x_2\) 的最短路径经过 \((u, v)\)。
然后我们再标记所有的 \((u, v)\) 的时间为 \(w\)。
接下来,我们再跑源点为 \(y_1, y_2\) 的单源最短路径 \(dis_3, dis_4\),\(y_1, y_2\) 为第二个人的起点与终点。
这时我们在更新 \(dis\) 的时候不仅要记录长度,还要记录时间,在进行比较的时候,长度为第一关键字,时间为第二关键字:长度越短越好;在长度相同的情况下,时间越长越好。
然后最后的答案就是 \({dis_3}_{y_2}\) 和 \({dis_4}_{y_1}\) 的时间取 \(\max\)。
是不是非常有趣呢?
因为点数比较小且边比较稠密,所以我们使用 \(O(n^2)\) 不带堆优化的 Dijkstra 进行计算。
代码
/*******************************
| Author: SunnyYuan
| Problem: P2149 [SDOI2009] Elaxia的路线
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2149
| When: 2023-09-28 23:11:54
|
| Memory: 128 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
#define d first
#define t second
using namespace std;
using PII = pair<int, int>;
const int N = 1510, INF = 0x3f3f3f3f;
int g[N][N];
int c[N][N];
int n, m;
int x1, y_1, x2, y2;
PII dis1[N], dis2[N], dis3[N], dis4[N];
bool vis[N];
bool cmp(PII a, PII b) {
if (a.d != b.d) return a.d < b.d;
return a.t > b.t;
}
void dijkstra(PII* dis, int S) {
for (int i = 1; i <= n; i++) {
dis[i] = {INF, -INF};
vis[i] = false;
}
dis[S] = {0, 0};
for (int i = 1; i <= n; i++) {
int p = -1;
for (int j = 1; j <= n; j++)
if ((!vis[j]) && (p == -1 || cmp(dis[j], dis[p])))
p = j;
vis[p] = true;
for (int j = 1; j <= n; j++) {
if (dis[j].d > dis[p].d + g[p][j]) {
dis[j].d = dis[p].d + g[p][j];
dis[j].t = dis[p].t + c[p][j];
}
else if (dis[j].d == dis[p].d + g[p][j]) dis[j].t = max(dis[j].t, dis[p].t + c[p][j]);
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
cin >> x1 >> y_1 >> x2 >> y2;
memset(g, 0x3f, sizeof(g));
for (int i = 1, u, v, w; i <= m; i++) {
cin >> u >> v >> w;
g[u][v] = g[v][u] = min(g[u][v], w);
}
dijkstra(dis1, x1);
dijkstra(dis2, y_1);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dis1[i].d + g[i][j] + dis2[j].d == dis1[y_1].d)
c[i][j] = g[i][j];
dijkstra(dis3, x2);
dijkstra(dis4, y2);
cout << max(dis3[y2].t, dis4[x2].t) << '\n';
return 0;
}
P9666 [ICPC2021 Macao R] Link-Cut Tree
本题解力求使用简单易懂的文字阐述道理。
思路
首先,我们可以推导出 \(2^1 + 2^2 + 2^3 + \cdots + 2^i = 2^{i + 1} - 1 < 2^{i + 1}\),说明我们就是选择了第 \(i + 1\) 条边前面的所有 \(i\) 条边,也不会去选第 \(i + 1\) 条边这一条边。
所以,我们要尽量往小的选,从小到大枚举边,只要什么时候形成了环,就退出。
我使用的是并查集判断环,然后题目要求输出环上的所有边,我用了 dfs 来找环。
是不是很简单呢?
代码
代码注释写的很详细,大家应该能看懂。
/*******************************
| Author: SunnyYuan
| Problem: P9666 [ICPC2021 Macao R] Link-Cut Tree
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P9666
| When: 2023-09-28 21:55:19
|
| Memory: 256 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using PII = pair<int, int>; // first : 点, second : 边的索引
const int N = 100010;
void solve() {
int n, m;
cin >> n >> m;
vector<int> fa(n);
vector<vector<PII> > e(n); // 并查集
vector<int> path; // 记录路径
iota(fa.begin(), fa.end(), 0); // 为 fa 赋值为 0 1 2 ... n - 1
auto find = [&](auto f, int x) -> int {// 找并查集的根
if (x == fa[x]) return x;
return fa[x] = f(f, fa[x]);
};
auto dfs = [&](auto f, int u, int fa, int des) -> bool {// 找环
if (u == des) return true; // 形成环,返回 true
for (auto to : e[u]) { // 遍历 u 的所有边
if (to.first == fa) continue;// 不能走回去
path.push_back(to.second); // 记录边的索引
if (f(f, to.first, u, des)) return true;// 找到答案,不用继续搜索
path.pop_back(); // 复原
}
return false; // 没找到 qwq
};
bool ok = false; // 是否已经找到答案
for (int i = 1, u, v; i <= m; i++) {
cin >> u >> v;
if (ok) continue; // 已经找到,但是也要让 cin 跑完
u--, v--;
e[u].push_back({v, i}); // 建图
e[v].push_back({u, i});
int fx = find(find, u), fy = find(find, v);// 并查集操作
if (fx == fy) { // 同根,找到环
path.push_back(i); // 当前这条边也不能丢哦
dfs(dfs, u, v, v); // 找环
ok = true; // 标记已经成功了
}
fa[fx] = fy; // 合并
}
if (ok) {
sort(path.begin(), path.end()); // 按照题目要求从小到大输出
for (int i = 0; i < path.size(); i++) cout << path[i] << " \n"[i == path.size() - 1];
}
else cout << "-1\n"; // 没找到 qwq
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T; // T 组数据
cin >> T;
while (T--) solve();
return 0;
}
P7414 [USACO21FEB] Modern Art 3 G
思路
考虑区间 DP。
设 \(f_{i, j}\) 表示要刷到 \([i, j]\) 这一段的目标需要的最小次数。
对于 \(f_{i, j}\),
如果 \(color_i\) 与 \(color_j\) 相等,那么再子区间合并的时候就可以少刷一次,即 \(f_{i, j} = \min\limits_{k = i}^{j - 1}f_{i, k} + f_{k + 1, j} - 1\)。
否则 \(f_{i, j} = \min\limits_{k = i}^{j - 1}f_{i, k} + f_{k + 1, j}\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 310, INF = 0x3f3f3f3f;
int f[N][N];
int n, a[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int len = 1; len <= n; len++) {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
if (len == 1) f[i][j] = 1;
else {
f[i][j] = INF;
for (int k = i; k < j; k++) {
if (a[i] == a[j]) f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] - 1);
else f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j]);
}
}
}
}
cout << f[1][n] << '\n';
return 0;
}
P7515 [省选联考 2021 A 卷] 矩阵游戏
思路
非常有意思的紫题。
首先,我们我们可以用已知条件算出一组 \(a_{i, j}\),即
因为题目要求的 \(a_{i, j}\) 需要满足 \(0 \le a_{i, j} \le 10^6\),所以我们考虑在每一个 \(a_{i, j}\) 上加上一个数字,可以进行如下构造:
即在第 \(i\) 行加上或减去一个数字 \(r_i\),第 \(j\) 列加上或减去一个数字 \(c_j\)。
那么,问题转化为 \(0 \le a_{i, j} + x \le 10^6\),那么 \(-a_{i, j} \le x \le 10^6 - a_{i, j}\)。
因为 \(x = r_i - c_j\) 或者 \(x = c_j - r_i\),简单一点,我们就假设 \(x = u - v\),那么 \(-a_{i, j} \le u - v \le 10^6 - a_{i, j}\),所以 \(v - u \le a_{i, j}\) 且 \(u - v \le 10^6 - a_{i, j}\)。
这是啥?这不就是差分约束吗?不会的可以参考我的博客
然后代码细节有点多,注意一下,然后就没有然后了。
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const i64 N = 2010, M = 720010, INF = 0x3f3f3f3f3f3f3f3f;
struct edge {
int to, next, w;
} e[M];
int head[N], idx = 1;
void add(int u, int v, int w) {
idx++, e[idx].to = v, e[idx].next = head[u], e[idx].w = w, head[u] = idx;
}
i64 dis[N];
bool st[N];
int cnt[N];
int n, m;
int a[N][N], b[N][N];
bool spfa(int u) {
deque<int> q;
q.emplace_back(u);
int ver = n + m;
for (int i = 1; i <= ver; i++) {
dis[i] = INF;
cnt[i] = 0;
st[i] = false;
}
dis[u] = 0;
st[u] = true;
while (q.size()) {
int t = q.front();
q.pop_front();
st[t] = false;
for (int i = head[t]; i; i = e[i].next) {
int to = e[i].to;
if (dis[to] > dis[t] + e[i].w) {
dis[to] = dis[t] + e[i].w;
cnt[to] = cnt[t] + 1;
if (cnt[to] >= ver) return false;
if (!st[to]) {
st[to] = true;
if (q.size() && dis[q.front()] >= dis[to]) q.emplace_front(to);
else q.emplace_back(to);
}
}
}
}
return true;
}
void process(int u, int v, int w) {
// -w <= u - v <= 1e6 - w
// -w <= u - v, v - u <= w
add(u, v, w);
add(v, u, 1e6 - w);
}
void solve() {
cin >> n >> m;
int ver = n + m;
for (int i = 0; i <= n; i++)
for (int j = 0; j <= m; j++)
a[i][j] = 0;
for (int i = 0; i <= ver; i++) head[i] = 0;
idx = 1;
for (int i = 1; i < n; i++)
for (int j = 1; j < m; j++)
cin >> b[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = b[i - 1][j - 1] - a[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if ((i & 1) && (j & 1)) process(i, j + n, a[i][j]);
else if ((i & 1) && (!(j & 1))) process(j + n, i, a[i][j]);
else if ((!(i & 1)) && (j & 1)) process(j + n, i, a[i][j]);
else if ((!(i & 1)) && (!(j & 1))) process(i, j + n, a[i][j]);
if (!spfa(1)) {
cout << "NO\n";
return;
}
cout << "YES\n";
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if ((i & 1) && (j & 1)) a[i][j] += dis[i] - dis[j + n];
else if ((i & 1) && (!(j & 1))) a[i][j] += dis[j + n] - dis[i];
else if ((!(i & 1)) && (j & 1)) a[i][j] += dis[j + n] - dis[i];
else if ((!(i & 1)) && (!(j & 1))) a[i][j] += dis[i] - dis[j + n];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cout << a[i][j] << " \n"[j == m];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P6880 [JOI 2020 Final] オリンピックバス
思路
我们考虑反转某一条边,如果 \((u, v)\) 不是 \(1\rightarrow n\) 或者 \(n\rightarrow 1\) 的最短路径上的一条边,那么对这张更新的图,我们的最小花费为 \(cost(u, v) + \min(dis_{1, n}, dis_{1, v} + w(u, v) + dis_{v, n}) + \min(dis_{n, 1}, dis_{n, v} + w(u, v) + dis_{u, 1})\),\(cost(u, v)\) 表示反转这条边的代价,\(w(u, v)\) 则是 \((u, v)\) 这条边的权值。
我们可以使用 Dijkstra 算法在正图和反图的源点为 \(1, n\) 各跑一遍 Dijkstra,总共 \(4\) 遍来快速计算上述距离。
否则,如果 \((u, v)\) 是 \(1\rightarrow n\) 或者 \(n\rightarrow 1\) 的最短路径上的一条边,那么就真的把边反转并跑 Dijkstra 计算距离,这样的边的数量为 \(O(n)\)。
然后,点数较少,所以不使用堆优化版本的 \(O(n ^ 2)\) 的 Dijkstra,然后总时间复杂度为 \(O(n^3)\)。
代码
不加 O2 过不了,我是新一代常数王者。
/*******************************
| Author: SunnyYuan
| Problem: P6880 [JOI 2020 Final] オリンピックバス
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P6880
| When: 2023-09-30 16:57:09
|
| Memory: 256 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const i64 N = 210, M = 100010, INF = 0x3f3f3f3f3f3f3f3f;
struct edge {
int to, next;
i64 c, d;
} e1[M], e2[M];
int head1[N], idx1 = 1;
int head2[N], idx2 = 1;
inline void add(edge e[] ,int head[], int& idx, int u, int v, int c, int d) {
idx++;
e[idx].to = v;
e[idx].next = head[u];
e[idx].c = c;
e[idx].d = d;
head[u] = idx;
idx++;
e[idx].to = u;
e[idx].next = head[v];
e[idx].c = INF;
e[idx].d = INF;
head[v] = idx;
}
int n, m;
i64 dis1[N], dis2[N], dis3[N], dis4[N], dis5[N], dis6[N];
int pre1[N], pre2[N], pre3[N], pre4[N], pre5[N], pre6[N];
bool is1[M], is2[M];
bool vis[N];
inline void dijkstra(i64* dis, int* pre, int s, edge e[], int head[]) {
memset(dis, 0x3f, sizeof(i64) * (n + 10));
memset(vis, false, sizeof(bool) * (n + 10));
memset(pre, 0, sizeof(int) * (n + 10));
dis[s] = 0;
for (int i = 1; i <= n; i++) {
int p = -1;
for (int j = 1; j <= n; j++)
if ((!vis[j]) && (p == -1 || dis[j] < dis[p]))
p = j;
vis[p] = true;
for (int j = head[p]; j; j = e[j].next) {
int to = e[j].to;
if (dis[to] > dis[p] + e[j].c) {
dis[to] = dis[p] + e[j].c;
pre[to] = j;
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1, u, v, c, d; i <= m; i++) {
cin >> u >> v >> c >> d;
add(e1, head1, idx1, u, v, c, d);
add(e2, head2, idx2, v, u, c, d);
}
dijkstra(dis1, pre1, 1, e1, head1);
dijkstra(dis2, pre2, n, e1, head1);
dijkstra(dis3, pre3, 1, e2, head2);
dijkstra(dis4, pre4, n, e2, head2);
int x = n;
while (x) {
is1[pre1[x]]= true;
x = e1[pre1[x] ^ 1].to;
}
x = 1;
while (x) {
is2[pre2[x]] = true;
x = e1[pre2[x] ^ 1].to;
}
i64 ans = dis1[n] + dis2[1];
for (int i = 2; i <= idx1; i += 2) {
int u = e1[i ^ 1].to, v = e1[i].to;
int cost = e1[i].d;
if (is1[i] || is2[i]) {
swap(e1[i].c, e1[i ^ 1].c);
swap(e2[i].c, e2[i ^ 1].c);
dijkstra(dis5, pre5, 1, e1, head1);
dijkstra(dis6, pre6, n, e1, head1);
swap(e1[i].c, e1[i ^ 1].c);
swap(e2[i].c, e2[i ^ 1].c);
ans = min(ans, dis5[n] + dis6[1] + cost);
}
else ans = min(ans, cost + min(dis1[n], dis1[v] + e1[i].c + dis4[u]) + min(dis2[1], dis2[v] + e1[i].c + dis3[u]));
}
if (ans < INF) cout << ans << '\n';
else cout << "-1\n";
return 0;
}
P2049 魔术棋子
思路
设 \(f_{i, j, k}\) 表示从原点走到 \((i, j)\) 模 \(m\) 后的乘积为 \(k\) 的方案数。
状态转移:\(f_{i, j, ka_{i, j} \bmod m} = f_{i - 1, j, k} + f_{i, j - 1, k}\)
统计答案:\(f_{n, n, k}\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m, o;
int a[N][N];
int f[N][N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> o;
for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) cin >> a[i][j];
f[1][1][a[1][1]] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
for (int k = 0; k < o; k++) {
// f[i][j - 1]
// f[i - 1][j]
f[i][j][(k * a[i][j]) % o] += f[i][j - 1][k];
f[i][j][(k * a[i][j]) % o] += f[i - 1][j][k];
}
}
}
vector<int> ans;
for (int k = 0; k < o; k++) if (f[n][m][k]) ans.push_back(k);
cout << ans.size() << '\n';
for (int x : ans) cout << x << ' ';
cout << '\n';
return 0;
}
P1119 灾后重建
思路
这是一道非常有意思的绿题。
我们发现这个题是对 Floyd 算法的很好的应用。
我们可以在每次往后延续时间的时候用新加入的点作为中转点更新所有的 \(dis_{i, j}\)。
\(Q\) 次询问一共加入 \(n\) 个点,每次更新 \(f_{i, j}\) 时间复杂度 \(O(n^2)\),总时间复杂度 \(O(n^3)\)。
代码
/*******************************
| Author: SunnyYuan
| Problem: P1119 灾后重建
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P1119
| When: 2023-10-02 09:08:09
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 210;
int n, m, q;
int t[N];
int g[N][N];
int x, y, l;
int dis[N][N];
bool vis[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> t[i];
memset(g, 0x3f, sizeof(g));
for (int i = 1, u, v, w; i <= m; i++) {
cin >> u >> v >> w;
u++, v++;
g[u][v] = g[v][u] = min(g[u][v], w);
}
cin >> q;
int cur = 1;
while (q--) {
cin >> x >> y >> l;
x++, y++;
if (t[x] > l || t[y] > l) {
cout << "-1\n";
continue;
}
while (t[cur] <= l && cur <= n) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (g[i][j] > g[i][cur] + g[cur][j])
g[i][j] = g[i][cur] + g[cur][j];
cur++;
}
if (g[x][y] < 0x3f3f3f3f) cout << g[x][y] << '\n';
else cout << "-1\n";
}
return 0;
}
P6033 [NOIP2004 提高组] 合并果子 加强版
参考了第 2 篇题解。
思路
这个题目我们必须使用 \(O(n)\) 的做法来完成。
首先,我们不难想到可以使用贪心的思想,每次选择最小的两个数字加起来再塞回去,这个可以使用优先队列来完成,但是时间复杂度有点高,要 \(O(n \log n)\),不能通过此题。
我们可以这样做:
因为 \(a_i\) 并不大,所以考虑使用桶排序。
然后将这些数字放到一个队列里面,然后再建立一个队列。
每次从这两个队列里面取出最小的数字并求和再放入第二个队列里面直到两个队列的元素数量之和等于 \(1\) 即可。
时间复杂度 \(O(n)\)。
代码
不加快读过不去,然后快读不用考虑负数的情况。
然后注意还要开 long long。
/*******************************
| Author: SunnyYuan
| Problem: P6033 [NOIP2004 提高组] 合并果子 加强版
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P6033
| When: 2023-10-02 11:04:15
|
| Memory: 512 MB
| Time: 500000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 10000010, M = 100010;
int n;
int c[M];
i64 q1[N], hh1, tt1;
i64 q2[N], hh2, tt2;
i64 getmin() {
i64 m1 = hh1 < tt1 ? q1[hh1] : 1e16, m2 = hh2 < tt2 ? q2[hh2] : 1e16;
if (m1 < m2) return q1[hh1++];
else return q2[hh2++];
}
int read() {
int x = 0;
char ch = getchar();
while (ch < '0' || ch > '9') ch = getchar();
while ('0' <= ch && ch <= '9') {
x = (x << 1) + (x << 3) + ch - '0';
ch = getchar();
}
return x;
}
int main() {
n = read();
for (int i = 1; i <= n; i++) {
c[read()]++;
}
for (int i = 0; i < M; i++) {
while (c[i]--) q1[tt1++] = i;
}
i64 sum = 0;
while (tt1 - hh1 + tt2 - hh2 > 1) {
i64 x = getmin(), y = getmin();
sum += x + y;
q2[tt2++] = x + y;
}
printf("%lld\n", sum);
return 0;
}
P7706 「Wdsr-2.7」文文的摄影布置
思路
我主要讲一讲怎么维护所有信息。
首先说一下基本思路,就是我们建立一棵线段树并在一个线段树上的节点 node 维护一个区间的:
struct node {
int maxa; // a 数组的区间最大值
int minb; // b 数组的区间最小值
int maxab; // 表示选择区间的两个数 i, j 满足 i < j 且要最大化 ai - bj
int maxba; // 表示选择区间的两个数 i, j 满足 i < j 且要最大化 aj - bi
int res; // 该区间的答案
};
那我们怎么维护这些信息呢?即怎么将子树的信息传到父节点呢?
首先因为我们要最大化,所以我们加的要尽量大,减的要尽量小。
然后,我们假设 rt 是存储父节点信息的结构体,lc, rc 表示存储左右子节点信息结构体,开始思考 pushup 函数怎么写。
因为维护信息太多了,所以我这里的 pushup 直接返回线段树节点了。
node pushup(node lc, node rc) {
node rt;
rt.maxa = max(lc.maxa, rc.maxa); // 即左右两个区间的最大值取较大值
rt.minb = min(lc.minb, rc.minb); // 即左右两个区间的最小值取较小值
rt.maxab = max(max(lc.maxab, rc.maxab), lc.maxa - rc.minb);// 即要么直接从子节点取出最大值,要么从左边取出 a 的最大值再减去右边 b 的最小值以达到最大化的目的
rt.maxba = max(max(lc.maxba, rc.maxba), rc.maxa - lc.minb);// 即要么直接从子节点取出最大值,要么从右边取出 a 的最大值再减去左边 b 的最小值以达到最大化的目的
rt.res = max(max(lc.res, rc.res), max(lc.maxab + rc.maxa, lc.maxa + rc.maxba));// 即要么直接从子节点取出答案,要么从左边取出 a + b 的最大值再加上右边 a 的最大值或者从左边取出 a 的最大值再加上右边 b + a 的最大值以达到最大化的目的
return rt;
}
其他的与线段树基本操作一样。
代码
/*******************************
| Author: SunnyYuan
| Problem: P7706 「Wdsr-2.7」文文的摄影布置
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P7706
| When: 2023-10-03 08:28:05
|
| Memory: 256 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 500010, INF = 1e9;
struct node {
int maxa; // a 数组的区间最大值
int minb; // b 数组的区间最小值
int maxab; // 表示选择区间的两个数 i, j 满足 i < j 且要最大化 ai - bj
int maxba; // 表示选择区间的两个数 i, j 满足 i < j 且要最大化 aj - bi
int res; // 该区间的答案
} tr[N << 2];
int n, m;
int a[N], b[N];
node pushup(node lc, node rc) {
node rt;
rt.maxa = max(lc.maxa, rc.maxa); // 即左右两个区间的最大值取较大值
rt.minb = min(lc.minb, rc.minb); // 即左右两个区间的最小值取较小值
rt.maxab = max(max(lc.maxab, rc.maxab), lc.maxa - rc.minb);// 即要么直接从子节点取出最大值,要么从左边取出 a 的最大值再减去右边 b 的最小值以达到最大化的目的
rt.maxba = max(max(lc.maxba, rc.maxba), rc.maxa - lc.minb);// 即要么直接从子节点取出最大值,要么从右边取出 a 的最大值再减去左边 b 的最小值以达到最大化的目的
rt.res = max(max(lc.res, rc.res), max(lc.maxab + rc.maxa, lc.maxa + rc.maxba));// 即要么直接从子节点取出答案,要么从左边取出 a + b 的最大值再加上右边 a 的最大值或者从左边取出 a 的最大值再加上右边 b + a 的最大值以达到最大化的目的
return rt;
}
void build(int u, int l, int r) {
if (l == r) {
tr[u] = {a[l], b[l], -INF, -INF, -INF};
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
tr[u] = pushup(tr[u << 1], tr[u << 1 | 1]);
}
node query(int u, int l, int r, int pl, int pr) {
if (pl <= l && r <= pr) return tr[u];
int mid = l + r >> 1;
if (pr <= mid) return query(u << 1, l, mid, pl, pr);
else if (pl > mid) return query(u << 1 | 1, mid + 1, r, pl, pr);
else return pushup(query(u << 1, l, mid, pl, pr), query(u << 1 | 1, mid + 1, r, pl, pr));
}
void modify(int u, int l, int r, int x, int v1, int v2) {
if (l == r) {
tr[u] = {v1, v2, -INF, -INF, -INF};
return;
}
int mid = l + r >> 1;
if (x <= mid) modify(u << 1, l, mid, x, v1, v2);
else modify(u << 1 | 1, mid + 1, r, x, v1, v2);
tr[u] = pushup(tr[u << 1], tr[u << 1 | 1]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
build(1, 1, n);
int opt, x, y;
while (m--) {
cin >> opt >> x >> y;
if (opt == 1) a[x] = y, modify(1, 1, n, x, a[x], b[x]);
else if (opt == 2) b[x] = y, modify(1, 1, n, x, a[x], b[x]);
else cout << query(1, 1, n, x, y).res << '\n';
}
return 0;
}
CF438D The Child and Sequence
思路
这个题目简直就是暴力上的明珠。
我们不需要打标记,可以直接线段树上暴力修改每一个值,但是会 TLE,所以我们要进行优化。
首先我们发现对一个数字 \(x\) 取模,只对比自己大的数字有作用,比如 \(5 \bmod 3 = 2\)(有用),\(2 \bmod 3 = 2\)(没用),所以我们可以记录一个区间最大值 \(\max\),如果取模的数字 \(x\) 大于 \(\max\),那么这个区间就不用取模了,这样做就可以 AC。
那这样为什么是对的呢?我们发现一个数字 \(n\) 取模 \(O(\log_2 n)\) 次就可以小于模数。
为什么呢?
因为当 \(2p \le n\),就有 \(p \le \dfrac{n}{2}\),那么 \(n \bmod p < p \le \dfrac{n}{2}\),所以 \(n \bmod p < \dfrac{n}{2}\),每次至少都要除以 \(2\),所以最多只要 \(\log_2 n\) 次。
当 \(p \le n < 2p\),那么 \(n \bmod p < p\),只需要一次。
所以一个数字 \(n\) 不断 \(\bmod\) 上一个大于 \(1\) 的数字,次数一定是 \(\log_2\) 级别的。
每次算上从线段树顶端往下走的次数 \(O(n \log_2n)\),总修改取模的时间复杂度为 \(O(n \log^2 n)\)。
询问的总时间复杂度:\(O(q \log n)\)。
修改某个数字的总时间复杂度:\(O(q \log n)\)。
再凭借着 Codeforces 比洛谷快 100 倍的评测机,这到题目就随便过了。
代码
/*******************************
| Author: SunnyYuan
| Problem: The Child and Sequence 孩子和序列
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF438D
| When: 2023-10-03 09:57:42
|
| Memory: 250 MB
| Time: 4000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010;
int n, m;
int a[N];
struct node {
i64 sum;
int max;
} tr[N << 2];
void pushup(int u) {
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
tr[u].max = max(tr[u << 1].max, tr[u << 1 | 1].max);
}
void build(int u, int l, int r) {
if (l == r) {
tr[u] = {a[l], a[l]};
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
void modify(int u, int l, int r, int x, int v) {
if (l == r) {
tr[u] = {v, v};
return;
}
int mid = l + r >> 1;
if (x <= mid) modify(u << 1, l, mid, x, v);
else modify(u << 1 | 1, mid + 1, r, x, v);
pushup(u);
}
void modify2(int u, int l, int r, int pl, int pr, int mod) {
if (tr[u].max < mod) return;
if (l == r) {
tr[u].sum %= mod;
tr[u].max %= mod;
return;
}
int mid = l + r >> 1;
if (pl <= mid) modify2(u << 1, l, mid, pl, pr, mod);
if (pr > mid) modify2(u << 1 | 1, mid + 1, r, pl, pr, mod);
pushup(u);
}
i64 query(int u, int l, int r, int pl, int pr) {
if (pl <= l && r <= pr) return tr[u].sum;
int mid = l + r >> 1;
if (pr <= mid) return query(u << 1, l, mid, pl, pr);
else if (pl > mid) return query(u << 1 | 1, mid + 1, r, pl, pr);
else return query(u << 1, l, mid, pl, pr) + query(u << 1 | 1, mid + 1, r, pl, pr);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
int opt, a, b, c;
while(m--) {
cin >> opt;
if (opt == 1) {
cin >> a >> b;
cout << query(1, 1, n, a, b) << '\n';
}
else if (opt == 2) {
cin >> a >> b >> c;
modify2(1, 1, n, a, b, c);
}
else {
cin >> a >> b;
modify(1, 1, n, a, b);
}
}
return 0;
}
P4145 / SP2713 GSS4 上帝造题的七分钟 2 / 花神游历各国
思路
上一题 CF438D 改一改就过了,详细见我的题解。
这到题目的思路就是当一个区间的最大值大于 \(1\) 时才处理 sqrt,否则对 \(1\) 不断 sqrt 也终究是 \(1\)。
就算 \(10^{18}\) 次不断 sqrt,也就 \(6\) 次就 sqrt 到了 \(1\),其他数字 sqrt 也大不到哪里去,根本不用担心 TLE。
代码
/*******************************
| Author: SunnyYuan
| Problem: P4145 上帝造题的七分钟 2 / 花神游历各国
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P4145
| When: 2023-10-03 11:11:27
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010;
int n, m;
i64 a[N];
struct node {
i64 sum;
i64 max;
} tr[N << 2];
void pushup(int u) {
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
tr[u].max = max(tr[u << 1].max, tr[u << 1 | 1].max);
}
void build(int u, int l, int r) {
if (l == r) {
tr[u] = {a[l], a[l]};
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
pushup(u);
}
void modify(int u, int l, int r, int pl, int pr) {
if (tr[u].max <= 1) return;
if (l == r) {
int x = sqrt(tr[u].sum);
tr[u].sum = x;
tr[u].max = x;
return;
}
int mid = l + r >> 1;
if (pl <= mid) modify(u << 1, l, mid, pl, pr);
if (pr > mid) modify(u << 1 | 1, mid + 1, r, pl, pr);
pushup(u);
}
i64 query(int u, int l, int r, int pl, int pr) {
if (pl <= l && r <= pr) return tr[u].sum;
int mid = l + r >> 1;
if (pr <= mid) return query(u << 1, l, mid, pl, pr);
else if (pl > mid) return query(u << 1 | 1, mid + 1, r, pl, pr);
else return query(u << 1, l, mid, pl, pr) + query(u << 1 | 1, mid + 1, r, pl, pr);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
cin >> m;
int opt, l, r;
while(m--) {
cin >> opt >> l >> r;
if (l > r) swap(l, r);
if (opt == 0) modify(1, 1, n, l, r);
else cout << query(1, 1, n, l, r) << '\n';
}
return 0;
}
P2135 方块消除
思路
大家为什么都假设往右边考虑呢?
我们来尝试一下新想法(老师要求写的)。
设 \(f_{i, j, k}\) 表示从合并 \(i\sim j\) 及 \(i\) 左边的 \(k\) 段,那么可以先分两部分合并:
或者在中间找到一个点分开,再进行合并:
代码
/*******************************
| Author: SunnyYuan
| Problem: P2135 方块消除
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2135
| When: 2023-10-03 19:17:33
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
int f[N][N][N], a[N], b[N], n;
int dfs(int l, int r, int k) {
if (f[l][r][k]) return f[l][r][k];
if (l == r) return f[l][r][k] = (b[l] + k) * (b[l] + k);
f[l][r][k] = dfs(l + 1, r, 0) + (b[l] + k) * (b[l] + k);
for (int i = l + 2; i <= r; i++)
if (a[i] == a[l])
f[l][r][k] = max(f[l][r][k], dfs(i, r, b[l] + k) + dfs(l + 1, i - 1, 0));
return f[l][r][k];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
cout << dfs(1, n, 0) << '\n';
return 0;
}
CF476E Dreamoon and Strings
思路
假设原串为 \(s\),匹配的串为 \(p\)。
我们设 \(last_i\) 表示从 \([last_i, i]\) 这一段区间里面能够选择出一个子序列等于 \(p\) 的最大值,那我们想要让这一段区间匹配上 \(p\),就需要删除 \(i - last_i + 1 - \operatorname{len}(p)\) 个元素。
这个 \(last_i\) 可以使用 \(O(n^2)\) 求出来。
然后我们考虑使用动态规划,设 \(f_{i, j}\) 表示考虑到了第 \(i\) 个元素,且删除了 \(j\) 个元素可以匹配 \(p\) 的最大个数。
首先,我们可以不删除任何数字,直接从 \(i - 1\) 推过来,即可以选择删除一个元素 \(i\),也可以选择不删元素 \(i\):
其次,我们可以完整地匹配一个串,匹配数量 \(+1\):
最终的答案就是删除 \(cnt\) 个,可以获得最大子串数量是 \(f_{n, cnt}\) 个。
代码
/*******************************
| Author: SunnyYuan
| Problem: Dreamoon and Strings
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF476E
| When: 2023-10-04 16:24:24
|
| Memory: 250 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 2010, INF = 0x3f3f3f3f;
char s[N], p[N];
int last[N];
int f[N][N];
int n, m;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> s + 1 >> p + 1;
n = strlen(s + 1), m = strlen(p + 1);
for (int i = 1; i <= n; i++) { // 计算 last 数组
int j = i, x = 0;
for (x = m; x >= 1; x--) {
while (j >= 1 && p[x] != s[j]) j--;
if (j < 1) break;
j--;
}
if (!x) last_i = j + 1;
else last_i = INF;
}
memset(f, -0x3f, sizeof(f)); // 动态规划
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= i; j++) {
f[i][j] = f[i - 1][j];
if (j) f[i][j] = max(f[i][j], f[i - 1][j - 1]);
if (last_i != INF && (j - (i - last_i + 1 - m)) >= 0) f[i][j] = max(f[i][j], f[last_i - 1][j - (i - last_i + 1 - m)] + 1);
}
}
for (int i = 0; i <= n; i++) cout << f[n][i] << ' ';
return 0;
}
CF401D Roman and Numbers
思路
- 把 \(n\) 放在二进制下研究每一个数位是否选取,最多有 18 位;
- 每次可以枚举选取的数字并拼接在原来的数字的最后;
- 设状态 \(f_{i, j}\) 表示选取的数字的状态在二进制下为 \(i\),拼成的整数模上 \(m\) 的余数为 \(j\) 的方案数;
- 答案为 \(f_{2^n - 1, 0}\)。
- 状态转移:\(f_{i, (10r + v_x) \bmod m} = f_{i - 2^x, r}\),假设选取第 \(x\) 个数字,之前的余数为 \(r\),现在的余数为 \(10r + v_x\),现在的状态为 \(i\),之前的状态没有包括 \(x\),为 \(i - 2^x\)。
- 初始状态:\(f_{0, 0} = 1\);
- 去重:设置 \(vis\) 数组,每次有新状态的时候清空,使用的时候标记该数字。
代码
/*******************************
| Author: SunnyYuan
| Problem: Roman and Numbers
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF401D
| When: 2023-10-04 18:49:29
|
| Memory: 500 MB
| Time: 4000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 18, M = 100;
i64 n, m;
i64 f[1 << N][M];
bool vis[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
vector<int> v;
while (n) v.push_back(n % 10), n /= 10;
f[0][0] = 1;
int sz = v.size();
for (int i = 1; i < (1 << sz); i++) {
memset(vis, 0, sizeof(vis));
for (int j = 0; j < sz; j++) {
if (i == (1 << j) && (!v[j])) continue;
if (i >> j & 1) {
if (vis[v[j]]) continue;
vis[v[j]] = true;
for (int k = 0; k < m; k++) {
f[i][(10 * k + v[j]) % m] += f[i - (1 << j)][k];
}
}
}
}
cout << f[(1 << sz) - 1][0] << '\n';
return 0;
}
P4198 楼房重建
思路
我们发现只有当选出楼房斜率越来越大才能全部看到,即 \(k_i = \dfrac{y_i}{x_i}\) 必须严格大于上一次选出的 \(k_j\)。
然后我们使用线段树对斜率进行维护,线段树中维护 \(cnt\) 表示在这个区间可以选择的最多的楼房数量,\(\max\) 表示在当前区间的最大的斜率。
现在的问题是怎么合并两个区间。
首先我们发现左边的区间的房屋可以全部保留:
然后我们再在右边找出所有大于左边区间最大斜率 \(\max_l\) 的房屋。
怎么找呢?
我们定义函数 query(u, l, r, x),表示在线段树上 \(u\) 节点管理的范围为 \([l, r]\),在这个区间找出斜率严格上升并且都大于 \(x\) 可以获得的最大数量,要达到“在右边找出所有大于左边区间最大斜率 \(\max_l\) 的房屋”的目的,可以直接调用 query(2 * u + 1, mid + 1, r, x)。
这个函数里面有些什么呢?
- 首先我们发现,如果当前询问区间的最大斜率没超过 \(x\),那就不可能选出任何房屋,直接返回 \(0\)。
- 如果询问节点 \(u\) 的左子节点 \(2u\) 对应区间的最大斜率没超过 \(x\),那么直接递归搜索右子节点 \(2u + 1\),因为在左边根本找不到。
- 否则,那就在左半边找出答案以后再加上右半边的答案,因为右半边是完整的且不受左边的影响,可以完整保留,就相当于整体的答案减去左半边的答案:\(cnt_u - cnt_{2u}\)。
然后就是在该修改的时候修改,在该合并的时候合并。
代码
/*******************************
| Author: SunnyYuan
| Problem: P4198 楼房重建
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P4198
| When: 2023-10-06 10:44:05
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
struct node {
int cnt;
double k;
} tr[N << 2];
int query(int u, int l, int r, double k) {
if (l == r) {
if (tr[u].k > k) return tr[u].cnt;
return 0;
}
int mid = l + r >> 1;
if (tr[u].k <= k) return 0;
if (tr[u << 1].k <= k) return query(u << 1 | 1, mid + 1, r, k);
else return query(u << 1, l, mid, k) + tr[u].cnt - tr[u << 1].cnt;
}
void pushup(int u, int l, int r) {
int mid = l + r >> 1;
tr[u].k = max(tr[u << 1].k, tr[u << 1 | 1].k);
tr[u].cnt = tr[u << 1].cnt + query(u << 1 | 1, mid + 1, r, tr[u << 1].k);
}
void modify(int u, int l, int r, int x, double v) {
if (l == r) {
tr[u] = {1, v};
return;
}
int mid = l + r >> 1;
if (x <= mid) modify(u << 1, l, mid, x, v);
else modify(u << 1 | 1, mid + 1, r, x, v);
pushup(u, l, r);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1, x, y; i <= m; i++) {
cin >> x >> y;
modify(1, 1, n, x, 1.0 * y / x);
cout << tr[1].cnt << '\n';
}
return 0;
}
CF940E Cashback
思路
我们发现两个区间分别的最小值之和大于等于一个区间最小值和次小值之和,所以我们要让区间划分的越多越好,那么我们要让每一个区间的长度越短越好,取长度为 \(c\) 时刚好可以使区间刚好删除一个数字并且划分出最多的区间。
接下来动态规划:
\(f_i = \min(f_{i - 1} + a_i, f_{i - c} + \sum\limits_{j = i - c + 1}^{i}a_i - \min\limits_{j = i - c + 1}^{i}a_i)\)
代码
/*******************************
| Author: SunnyYuan
| Problem: Cashback
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF940E
| When: 2023-10-05 19:23:19
|
| Memory: 250 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 100010;
int n, a[N], c;
i64 f[N], sum[N];
int st[N][25];
void initst() {
for (int j = 1; j < 25; j++)
for (int i = 1; i + (1 << j) - 1 <= n; i++)
st[i][j] = min(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
}
int getmin(int l, int r) {
int len = r - l + 1;
int lg = __lg(len);
return min(st[l][lg], st[r - (1 << lg) + 1][lg]);
}
i64 getsum(int l, int r) {
return sum[r] - sum[l - 1];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> c;
for (int i = 1; i <= n; i++) cin >> a[i], sum[i] = sum[i - 1] + a[i], st[i][0] = a[i];
for (int i = 1; i < c; i++) f[i] = f[i - 1] + a[i];
initst();
for (int i = c; i <= n; i++) {
f[i] = f[i - 1] + a[i];
f[i] = min(f[i], f[i - c] + getsum(i - c + 1, i) - getmin(i - c + 1, i));
}
cout << f[n] << '\n';
return 0;
}
CF906C Party
思路
这是一道非常有意思的状压 DP 题目。
首先,我们默认从 \(0\) 开始计数,即下标都从 \(0\) 开始,所有人的编号从 \(0\) 到 \(n - 1\)。
首先,我们设 \(f_{state}\) 表示要达到状态为 \(state\) 需要的最小步骤,假设 \(state_i\) 表示 \(state\) 在二进制表示下的第 \(i\) 位,那么 \(state_i = 1\) 构成的 \(i\) 的集合表示这些人互相认识,比如 \(state = 11011\),表示第 \(0, 1, 3, 4\) 个人互相认识。
然后假设 \(a_i\) 表示第 \(i\) 个人直接认识的人,即如果 \(a_i\) 的二进制表示下的第 \(j\) 位 \(a_{i, j}\) 为 \(1\),那么表示 \(i, j\) 直接认识。
再然后就是枚举所有的状态 \(state\),如果 \(state_i\) 为 \(1\),那么就可以让第 \(i\) 个人进行介绍,状态变为 \(state\) 或 \(a_i\)。
下面是重点,就是我们怎么输出状态:
我们可以记录一个 \(prestate\) 表示 \(state\) 在动态规划上是从哪个状态来的,\(prepeo\) 表示从 \(prestate\) 经过了 \(prepeo\) 的介绍才来到了 \(state\) 状态。
所以我们可以直接弄一个递归函数,一直认祖归宗直到某一个起点,再从前往后输出。
注意我们要先递归再输出,因为我们要从里到外介绍才能保证第 \(i\) 个人介绍的时候他自己已经被介绍。
代码
/*******************************
| Author: SunnyYuan
| Problem: Party
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF906C
| When: 2023-10-05 17:29:41
|
| Memory: 250 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 22;
int n, m, a[N], f[1 << N], pre_state[1 << N], pre_peo[1 << N];
void dfs(int state) {
if (!state) return;
if (pre_peo[state] != -1) cout << pre_peo[state] + 1 << ' ';
dfs(pre_state[state]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
if (m == n * (n - 1) / 2) {
cout << 0 << '\n';
return 0;
}
for (int i = 1, u, v; i <= m; i++) {
cin >> u >> v;
u--, v--;
a[u] |= 1 << v;
a[v] |= 1 << u;
}
memset(f, 0x3f, sizeof(f));
for (int i = 0; i < n; i++) f[1 << i] = 0, pre_peo[1 << i] = -1;
for (int i = 0; i < (1 << n); i++)
for (int j = 0; j < n; j++)
if ((i >> j & 1) && f[i | a[j]] > f[i] + 1) {
f[i | a[j]] = f[i] + 1;
pre_state[i | a[j]] = i;
pre_peo[i | a[j]] = j;
}
cout << f[(1 << n) - 1] << '\n';
dfs((1 << n) - 1);
return 0;
}
CF1025D Recovering BST
思路
这里讲一个通俗易懂的版本。
设 \(f_{i, j, 0/1}\) 表示在 \([i, j]\) 这一段区间以 \(i\) 或者 \(j\) 为根是否可以建成二叉搜索树。如果 \(f_{i, j, 0} = true\) 表示以 \(i\) 为根建立一棵二叉搜索树可行,\(f_{i, j, 1} = true\) 表示以 \(j\) 为根建立一棵平衡树可行。
那我们想让 \(i\) 为根,首先要让 \([i + 1, j]\) 成为其右子树,那我们要选出来一个根 \(k\) 满足 \(i + 1 \le k \le j\),那么我们要让 \(k\) 成为 \([i + 1, j]\) 这个区间的根,就要让 \(f_{i + 1, k, 1}\) 和 \(f_{k, j, 0}\) 都是 \(true\),保证两棵子树都能接在 \(k\) 上,然后我们再让 \(i, k\) 相连,那么就需要满足 \(\gcd(a_i, a_k) > 1\) 才行,如果以上条件都满足,那么 \(f_{i, j, 0}\) 为 \(true\),可以以 \(i\) 为根。
同样的,我们想让 \(j\) 为根,首先要让 \([i, j - 1]\) 成为左子树,然后找出一个根 \(k\) 保证左右子树可以和谐相处,还要保证 \(\gcd(a_j, a_k) > 1\),如果以上条件都满足,那么 \(f_{i, j, 1}\) 为 \(true\)。
最后答案 \(f_{1, n, 0}\) 或 \(f_{1, n, 1}\) 为真。
代码
/*******************************
| Author: SunnyYuan
| Problem: Recovering BST
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF1025D
| When: 2023-10-05 16:16:26
|
| Memory: 250 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 710;
bool f[N][N][2], c[N][N];
int n, a[N];
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j++)
c[i][j] = gcd(a[i], a[j]) > 1;
for (int len = 1; len <= n; len++) {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
if (len == 1) f[i][i][0] = f[i][i][1] = 1;
else {
for (int k = i + 1; k <= j; k++) if (f[i + 1][k][1] && f[k][j][0] && c[i][k]) f[i][j][0] = true;
for (int k = i; k <= j - 1; k++) if (f[i][k][1] && f[k][j - 1][0] && c[k][j]) f[i][j][1] = true;
}
}
}
if (f[1][n][1] || f[1][n][0]) cout << "Yes\n";
else cout << "No\n";
return 0;
}
P2656 采蘑菇
思路
这到题目非常简单,非常适合初学者。
首先我们用 Tarjan 求出所有强连通分量,每个强连通分量的所有边都可以被取光,然后连接各个强连通分量的边只能取一次。
然后我们算出每条边真实可以取的蘑菇数量,然后 dfs 一遍求出答案就可以了,然后就没有然后了。
代码
/*******************************
| Author: SunnyYuan
| Problem: P2656 采蘑菇
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/P2656
| When: 2023-10-05 14:51:39
|
| Memory: 125 MB
| Time: 1000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 80010, M = 200010;
struct edge {
int to, next, w;
int t;
} e[M];
int head[N], idx;
void add(int u, int v, int w, double t) {
idx++, e[idx].to = v, e[idx].next = head[u], e[idx].w = w, e[idx].t = t, head[u] = idx;
}
int n, m;
int dfn[N], low[N], tot;
int s[N], top;
int scc[N], cnt;
bool stk[N];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
stk[u] = true; s[++top] = u;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (!dfn[to]) {
tarjan(to);
low[u] = min(low[u], low[to]);
}
else if (stk[to]) low[u] = min(low[u], dfn[to]);
}
if (low[u] == dfn[u]) {
cnt++;
while (s[top] != u) {
scc[s[top]] = cnt;
stk[s[top]] = false;
top--;
}
scc[u] = cnt;
stk[u] = false;
top--;
}
}
int getsum(int x, int t) {
int sum = 0;
while (x) {
sum += x;
x = x * t / 10;
}
return sum;
}
int sum[N], ans, res;
vector<int> g[N];
vector<int> w[N];
void dfs(int u) {
ans += sum[u];
int sz = g[u].size();
for (int i = 0; i < sz; i++) {
int to = g[u][i], p = w[u][i];
ans += p;
dfs(to);
ans -= p;
}
if (!sz) res = max(res, ans);
ans -= sum[u];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v, w;
string s;
cin >> u >> v >> w >> s;
if (s == "0") add(u, v, w, 0);
else add(u, v, w, s[2] - '0');
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; i++) {
for (int j = head[i]; j; j = e[j].next) {
int to = e[j].to;
if (scc[i] == scc[to]) sum[scc[i]] += getsum(e[j].w, e[j].t);
else g[scc[i]].push_back(scc[to]), w[scc[i]].push_back(e[j].w);
}
}
int s;
cin >> s;
s = scc[s];
dfs(s);
cout << res << '\n';
return 0;
}
CF721C Journey
思路
非常有意思的入门拓扑排序题目。
设 \(f_{i, j}\) 表示到点 \(i\) 经过了 \(j\) 个点的最短路径。
因为是个 DAG,所以我们先进行拓扑排序,然后从前往后进行枚举。
对于每一条边 \((u, v)\) 有 \(f_{to, a} = \min(f_{to, a}, f_{u, a - 1} + w)\)。
最后答案是 \(\max\limits_{f_{n, i} \le k} i\),然后第二问就在 DP 中记录来的状态,最后倒退回去就可以了。
代码
/*******************************
| Author: SunnyYuan
| Problem: Journey
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF721C
| When: 2023-10-05 12:55:20
|
| Memory: 250 MB
| Time: 3000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using PII = pair<int, int>;
const int N = 5010;
int n, m, k;
vector<int> e[N], w[N];
vector<int> ans;
queue<int> q;
int in[N];
int f[N][N];
int pre[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> k;
for (int i = 1, u, v, p; i <= m; i++) {
cin >> u >> v >> p;
e[u].push_back(v);
w[u].push_back(p);
in[v]++;
}
for (int i = 1; i <= n; i++) if (!in[i]) q.push(i);
while (q.size()) {
int t = q.front();
q.pop();
ans.push_back(t);
int sz = e[t].size();
for (int i = 0; i < sz; i++) {
int to = e[t][i];
in[to]--;
if (!in[to]) q.push(to);
}
}
memset(f, 0x3f, sizeof(f));
f[1][1] = 0;
for (auto x : ans) {
for (int i = 1; i <= n; i++) {
int sz = e[x].size();
for (int j = 0; j < sz; j++) {
int to = e[x][j], p = w[x][j];
if (f[to][i + 1] > f[x][i] + p) {
f[to][i + 1] = f[x][i] + p;
pre[to][i + 1] = x;
}
}
}
}
int p = -1;
for (int i = 1; i <= n; i++) {
if (f[n][i] <= k) p = i;
}
cout << p << '\n';
stack<int> s;
int x = n, y = p;
while (x) {
int p = pre[x][y];
s.push(x);
x = p;
y--;
}
while (s.size()) {
cout << s.top() << ' ';
s.pop();
}
return 0;
}
CF1051D Bicolorings
思路
这里给出一种简单的实现方式,首先说一下基本思路:
设 \(f_{i, j, k}\) 表示染到了 \(i\) 列,共 \(j\) 个连通块,第 \(i\) 列的状态为 \(k\) 的方案数,下图是状态 \(k\) 对应的染法:
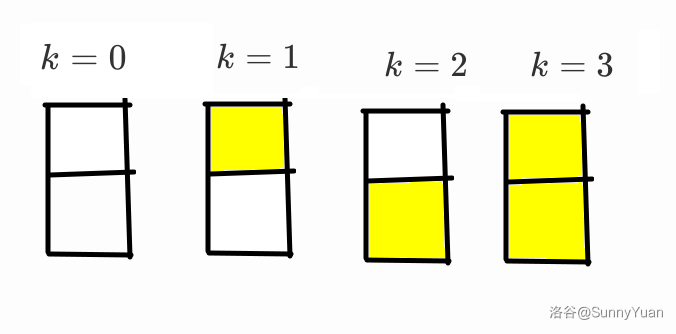
然后我们可以记一个 \(add\) 数组,\(add_{i, j}\) 表示上一列是状态 \(i\),这一列状态是 \(j\) 对连通块数量的变化。
int add[4][4] = {
0, 1, 1, 1,
0, 0, 2, 0,
0, 2, 0, 0,
1, 1, 1, 0
};
然后,我们枚举列数 \(i\),连通块数量为 \(cur\),以及上一列的状态为 \(k\) 及这一列的状态为 \(j\) 然后进行转移即可:
\(f_{i, cur, j} = \sum f_{i - 1, cur - add_{k, j}, k}\)
初始化:\(f_{1, 1, 0} = f_{1, 2, 1} = f_{1, 2, 2} = f_{1, 1, 3} = 1\)
结果:\(f_{n, k, 0} + f_{n, k, 1} + f_{n, k, 2} + f_{n, k, 3}\)。
代码
代码非常简单,不知道为什么大佬的代码都很长。
/*******************************
| Author: SunnyYuan
| Problem: Bicolorings
| Contest: Luogu
| URL: https://www.luogu.com.cn/problem/CF1051D
| When: 2023-10-04 19:36:00
|
| Memory: 250 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 2010, mod = 998244353;
int n, k;
int f[N][M][4];
int add[4][4] = {
0, 1, 1, 1,
0, 0, 2, 0,
0, 2, 0, 0,
1, 1, 1, 0
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k;
f[1][1][0] = f[1][2][1] = f[1][2][2] = f[1][1][3] = 1;
for (int i = 2; i <= n; i++) {
for (int cur = 1; cur <= k; cur++) {
for (int j = 0; j < 4; j++) {
for (int k = 0; k < 4; k++) {
if (cur > add[k][j]) (f[i][cur][j] += f[i - 1][cur - add[k][j]][k]) %= mod;
}
}
}
}
cout << ((f[n][k][0] + f[n][k][1]) % mod + (f[n][k][2] + f[n][k][3]) % mod) % mod << '\n';
return 0;
}

