Tarjan 算法、割点、割边、边双连通分量、点双连通分量
来自我的洛谷专栏。
强连通分量
定义
有向图 \(G\) 中任意两个点都可以互相到达就称这个有向图 \(G\) 强连通。
强连通分量就是极大的强连通子图。
Tarjan 算法
思路
Tarjan 算法可以用来求强连通分量,其思想是建立一棵搜索树,维护 \(\text{dfn, low}\),简单来说就是 \(\text{dfn}\) 就是在 dfs 时是第几个遍历到的,\(\text{low}\) 就是从一个点出发不经过树边可以到达的最小的 \(\text{dfn}\)。
当 \(\text{dfn[u] = low[u]}\) 时说明点 \(u\) 是第一个访问其所在连通块的节点,整个连通块中的节点都在以 \(u\) 为根的子树中。
注意:上面这句话是指,整个连通块在子树中,而不是整个子树都是一个强连通分量。
同时,我们维护一个栈,它里面的元素与 dfs 的栈不太相同,它保存的是在 dfs 的过程中还没有将它们划分为强连通分量的点。
所以在 dfs 时当 \(u\) 与 \(v\) 有边相连,对于 \(v\) 有 3 种情况:
- \(v\) 还没有被访问过,即 \(\text{dfn[v] = 0}\)(假设 \(\text{dfn}\) 都被初始化为 \(0\)),那么就遍历 \(v\),即 \(\text{dfs(v)}\) 并且更新 \(\text{low[u] = min(low[u], low[to])}\)。
- \(v\) 被访问过且在栈中,即 \(\text{stk[v] = true}\),说明该元素还没有被处理,那么更新 \(\text{low[u] = min(low[u], dfn[to])}\)。
- \(v\) 被访问过且不在栈中,说明元素已经被处理完了,略过。
代码
只写了最基础的部分,没有写统计的部分。
注意到 else if 后面的 low[u] = min(low[u], dfn[to]),为什么不能写 low[u] = min(low[u], low[to]),等会讲割点的时候说。
注意:else if 那里更新 low 时一定要判断结点是否在栈中!(感性理解一下,这是有向图,处理完的就不能再回去了)
bool stk[N];
int s[N], top;
int low[N], dfn[N], tot, ans;
void tarjan(int u) {
s[++top] = u;
stk[u] = true;
low[u] = dfn[u] = ++tot;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (!dfn[to]) {
tarjan(to);
low[u] = min(low[u], low[to]);
}
else if (stk[to]) low[u] = min(low[u], dfn[to]);
}
if (low[u] == dfn[u]) {
while (s[top] != u) {
stk[s[top]] = false;
top--;
}
stk[u] = false;
top--;
}
}
可以将P2863 [USACO06JAN] The Cow Prom S作为模板题。
缩点
使用上述 Tarjan 算法将一个强连通分量当作一个点并互相连接,然后可以使用有关有向无环图的做法处理新图。
例题
这个题目我使用的是拓扑排序处理和。注意一定要判断连接的两个点是否处于同一个强连通分量,否则会在新图酿成自环而无法使用拓扑排序(!!!)
#include <bits/stdc++.h>
using namespace std;
const int N = 20010, M = 200010;
struct edge {
int to, next;
} e[M];
int head[N], head2[N], idx;
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
}
void add2(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head2[u], head2[u] = idx;
}
int n, m, a[N];
int dfn[N], low[N], cnt, stk[N], top, instk[N];
vector<int> gd[N];
int belong[N];
int tot;
int sum[N];
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
stk[++top] = u; instk[u] = true;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (!dfn[to]) {
tarjan(to);
low[u] = min(low[u], low[to]);
}
else if (instk[to]) low[u] = min(low[u], dfn[to]);
}
if (low[u] == dfn[u]) {
tot++;
while (stk[top] != u) {
belong[stk[top]] = tot;
gd[tot].push_back(stk[top]);
sum[tot] += a[stk[top]];
instk[stk[top]] = false;
top--;
}
instk[u] = false;
gd[tot].push_back(u);
sum[tot] += a[u];
belong[u] = tot;
top--;
}
}
int in[N], out[N], f[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
add(u, v);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) {
top = 0;
tarjan(i);
}
}
for (int k = 1; k <= tot; k++) {
for (auto x : gd[k]) {
for (int i = head[x]; i; i = e[i].next) {
int to = e[i].to;
if (k == belong[to]) continue;
add2(k, belong[to]);
out[k]++;
in[belong[to]]++;
}
}
}
for (int i = 1; i <= tot; i++) f[i] = sum[i];
queue<int> q;
for (int i = 1; i <= tot; i++) {
if (!in[i]) {
q.push(i);
}
}
while (q.size()) {
int t = q.front();
q.pop();
for (int i = head2[t]; i; i = e[i].next) {
int to = e[i].to;
in[to]--;
f[to] = max(f[to], f[t] + sum[to]);
if (!in[to]) q.push(to);
}
}
int ans = 0;
for (int i = 1; i <= tot; i++) ans = max(ans, f[i]);
cout << ans << '\n';
return 0;
}
割点
定义
在一个无向图中,如果将一个点及与该点相连的边删除后连通分量会被断开分为 \(2\) 个及以上,这个点就是一个割点。
性质一:无向图至少有 3 个点才可能有割点。
性质二:dfs搜索树中的根结点有 2 个及以上的子节点时,才可能是割点。
思路
\(\text{low}\) 数组现在表示在不经过搜索树上的父亲节点可以到达的最小 \(\text{dfn}\)。
主要是通过 \(\text{low}\) 数组判断,如果对于一个不是搜索树的根节点 \(u\) 的子节点 \(v\),\(\text{low[v]} \ge \text{dfn[u]}\),那说明 \(v\) 如果不通过 \(u\) 根本就回不去了,就不能再见到祖宗了,说明 \(u\) 就是一个割点。
对于一个搜索树的根节点,如果其儿子节点的个数大于等于 \(2\),那么如果把这个点删除,它的儿子就不互通,它也是一个割点,如果有环一个点走着走着又回来了只算作一个儿子。
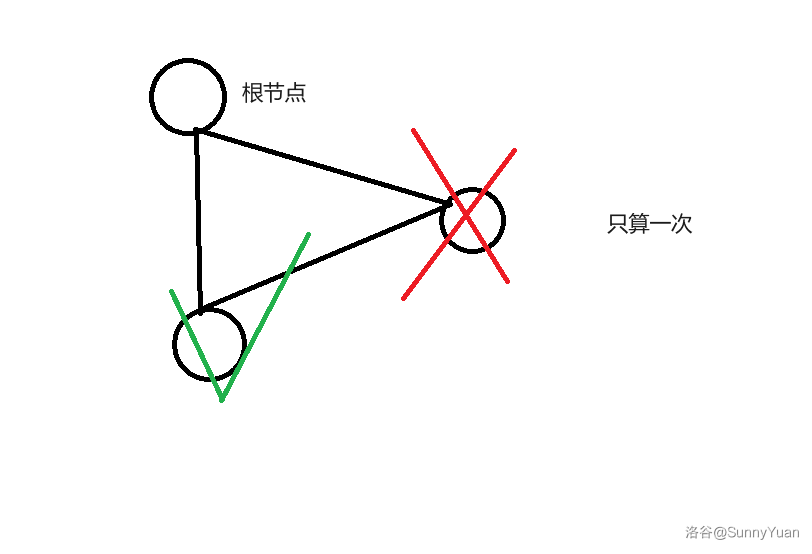
代码
P3388 【模板】割点(割顶)关键代码
upd 7/16/2024
注意:else if 那里写的是 to != fa,表示不经过父结点能回到的点,而不是有向图中求强连通分量的判断是否在栈中。
struct edge {
int to, next;
} e[M];
int head[N], idx = 1;
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
}// 建图
int dfn[N], low[N], cnt, ans;
bool cut[N];
vector<int> ver;
int root;
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++cnt;
int child = 0;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (!dfn[to]) {
child++;// 统计子结点个数
tarjan(to, u);
low[u] = min(low[u], low[to]);
if (u != root && (!cut[u]) && low[to] >= dfn[u]) { // u != fa:不是根结点,!cut[u]:未被标记,low[to] >= dfn[u] : 回不去了,u 是隔点
cut[u] = true;
ans++;
ver.push_back(u);
}
}
else if (to != fa) low[u] = min(low[u], dfn[to]);
}
if (u == root && (!cut[u]) && child > 1) { // 处理根结点
cut[u] = true;
ver.push_back(u);
ans++;
}
}
... ... ... ...
for (int i = 1; i <= n; i++) {
if (!dfn[i]) {
root = i;
tarjan(i, i);
}
}
写割点时 low[u] = min(low[u], dfn[to]) 为什么不能写 low[u] = min(low[u], low[to]) 呢?
比如这个图:
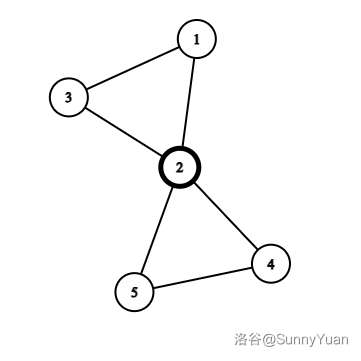
假如遍历顺序为 \(1, 3, 2, 5, 4\),你会发现当遍历到 \(2\) 的时候,\(\text{dfn[2] = 3,low[2] = dfn[1] = 1}\),然后继续运行,到 \(4\) 的时候会 low[u] = min(low[u], low[to]),\(\text{to}\) 此时为 \(2\),那么 \(\text{low[4] = low[2] = 1}\),相当于不用经过点 \(2\) 就回到了 \(1\),违背了刚刚的定义(可以翻到上面看割点思路标题下的第一句话),但是如果 low[u] = min(low[u], dfn[to]),\(\text{low[4] = dfn[2] = 2}\),是正确的,\(4\) 只能回到 \(2\)。
割边
定义
把割点的定义复制过来改一改
在一个无向图中,如果将一条边删除后原来的连通分量被分成了 \(2\) 个,这条边就是一条割边。(我的理解)
思路
我们直接将上面的割点的 \(\text{low[v]} \ge \text{dfn[u]}\) 改为 \(\text{low[v]} > \text{dfn[u]}\) 就可以了,表示出去了就再也回不到 \(u\) 了,所以当 \(\text{low[v]} > \text{dfn[u]}\),那么 \((u, v)\) 就是一条割边。
割边代码不需要判断当前点是否为根,因为点和边还是有区别的,一条边可以把分量分成两个部分,但是换成点,删除根节点,分量数量有可能不会发生改变。
代码
用了链式前向星,好标记。
struct edge {
int to, next;
} e[M];
int head[N], idx = 1;
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
}
int dfn[N], low[N], tot, ans; // ans : 割边数量
bool cut[N];
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++tot;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (!dfn[to]) {
tarjan(to, u);
low[u] = min(low[u], low[to]);
if (low[to] > dfn[u]) {
if (!cut[i]) ans++;
cut[i] = cut[i ^ 1] = true;// i 和 i ^ 1 是算法竞赛中常用的反边标记方法,可以将奇偶互相转化
}
}
else if (to != fa) low[u] = min(low[u], dfn[to]);
}
}
可以将P1656 炸铁路 作为模板题,只是数据范围有点小,在此题中可以直接拿 vector 存储答案,不需要标记边,但是下一节边双需要用到。
边双连通分量
定义
在一个无向图中,对于一个分量,删除任意一条边都不会影响任意两点之间的连通性,这个分量就是边双连通分量。(我理解的)
思路
我们发现在一个边双连通分量不可能有割边,所以我们发现只要把整个图的割边拿出来作为分隔不同的边双连通分量就可以了。
代码
P8436 【模板】边双连通分量的关键代码
struct edge {
int to, next;
} e[M];
int head[N], idx = 1;
void add(int u, int v) {
idx++, e[idx].to = v, e[idx].next = head[u], head[u] = idx;
}
int n, m;
int dfn[N], low[N], tot, cut[M];
bool stk[N];
void tarjan(int u, int fa) {// 求割边
dfn[u] = low[u] = ++tot;
stk[u] = true;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (!dfn[to]) {
tarjan(to, u);
low[u] = min(low[u], low[to]);
if (low[to] > dfn[u]) cut[i] = cut[i ^ 1] = true;
}
else if (to != fa) low[u] = min(low[u], dfn[to]);
}
}
vector<int> ans[N];
int p[N];
int cnt;
void dfs(int u, int s) { // 进行划分
p[u] = s;
ans[s].push_back(u);
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (cut[i] || p[to]) continue; // 不走割边及不重复访问
dfs(to, s);
}
}
int main() {
// ... 输入
for (int i = 1; i <= n; i++)
if (!dfn[i])
tarjan(i, i);
for (int i = 1; i <= n; i++) {
if (!p[i]) {
dfs(i, ++cnt);
}
}
cout << cnt << '\n';
for (int i = 1; i <= cnt; i++) {
cout << ans[i].size() << ' ';
for (int x : ans[i]) cout << x << ' ';
cout << '\n';
}
return 0;
}
点双连通分量
定义
一个图的点双连通极大子图就是点双连通分量,即删去任意一个点,其他点也是连通的。
点双连通分量:无向图中的极大点双连通子图称为 V-DCC。
注意:点双连通不具有传递性,边双连通具有传递性。
性质
性质一:1 个割点可能在多个点双中。
upd 9/22/2023
- 点双连通分量中没有割点;
- 不同的点双连通分量只有至多一个公共点(割点);
- 任意一个割点都是至少两个点的点双连通公共点。
——来自《算法竞赛》一书。
思路
如果对于任意一个点 \(u\),存在子节点 \(to\),使得 \(\text{low[to]} \ge \text{dfn[u]}\),那么管它是不是根节点都要进行统计。
怎么统计呢,我们从栈里不断弹出,直到 \(to\),这些弹出的点和 \(u, to\) 都是这个连通分量里的。
upd 9/22/2023
为什么不直接到 \(u\) 呢?参见我发的讨论。
代码
P8435 【模板】点双连通分量 的关键代码。
const int N = 500010, M = 4000010;
vector<int> e[N];
int dfn[N], low[N], tot;
int s[N], top;
bool cut[N];
vector<int> ans[N];
int cnt;
int root;
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++tot;
if (u == root && e[u].empty()) { // 当图中只有一个根结点,那么这个点就是一个点双
cnt++;
ans[cnt].push_back(u);
return;
}
s[++top] = u;
int ch = 0;
for (int to : e[u]) {
if (!dfn[to]) {
ch++;
tarjan(to, u);
low[u] = min(low[u], low[to]);
if (low[to] >= dfn[u]) {
cut[u] = true;
cnt++;
int p = s[top];
do {
p = s[top];
ans[cnt].push_back(p);
top--;
} while (p != to);
ans[cnt].push_back(u);
}
}
else if (to != fa) low[u] = min(low[u], dfn[to]);
}
}
int n, m;
int main() {
// ... 输入
for (int i = 1; i <= n; i++)
if (!dfn[i]) {
root = i;
tarjan(i, i);
}
cout << cnt << '\n';
for (int i = 1; i <= cnt; i++) {
cout << ans[i].size() << ' ';
for (int x : ans[i]) cout << x << ' ';
cout << '\n';
}
return 0;
}

