Aho-Corasick自动机(AC自动机)
AC自动机 (Aho-Corasick Algorithm)。
AC自动机是多模匹配算法,在一个文本串 \(T\) 中查找多个不同的模式串 \(S\)。
多模匹配问题:给定一个长为 \(n\) 的文本 \(S\), 以及 \(k\) 个平均长度为 \(m\) 的模式串 \(P_1, P_2, \dots, P_k\)
AC自动机思想
AC自动机思想:AC 自动机 = 用字典树组织多个模式串 + KMP避免回溯。
AC自动机的构造
文中 \(字母(数字)\) 表示节点编号为 \(数字\) 的 \(字母\)。
举例:
\(abcd, b, cd\)
- 先把所有的模式串建成字典树,节点0是分界点,不存储字符。
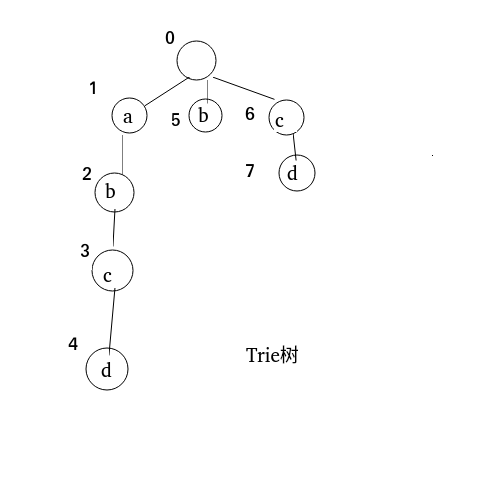
- 再建立Fail指针, 一个节点 \(x\) 的Fail指针指向的节点是“父节点的Fail指针所指向的节点的与 \(x\) 同字符的子节点”。 通过这样的赋值, \(x\) 得到了这个同字符节点的后缀关系(不懂可以继续往下看)。
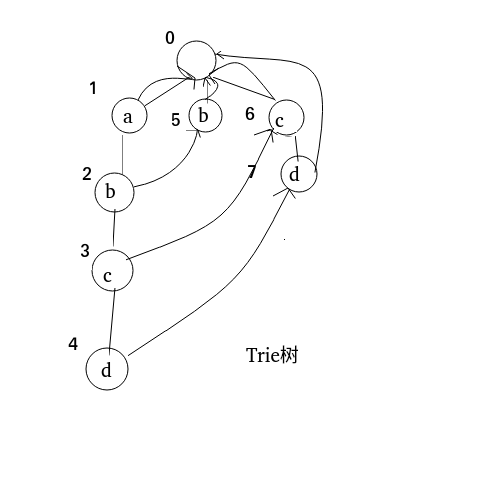
Fail指针的计算
Fail指针的计算,可以使用BFS进行处理。
分为两种情况:
如上图:
-
\(b\) 的处理很简单,就是父亲 \(a\) 的Fail节点 \(0\) 指向的 \(b(5)\)。
-
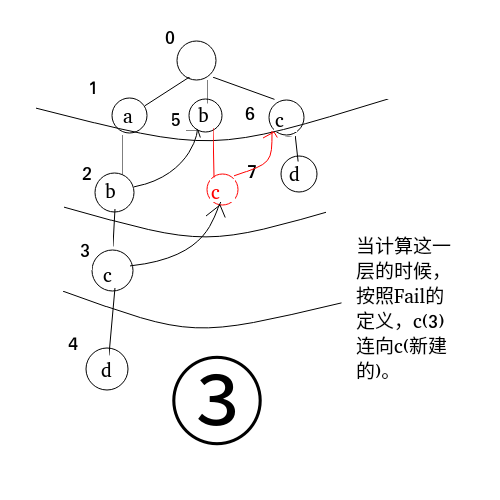
但要处理 \(c\) 的较为麻烦,有如下步骤:
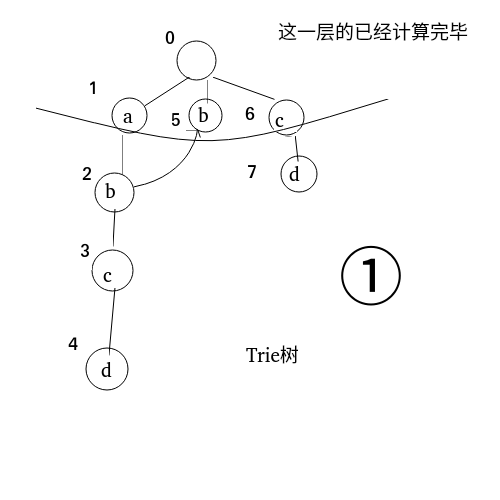
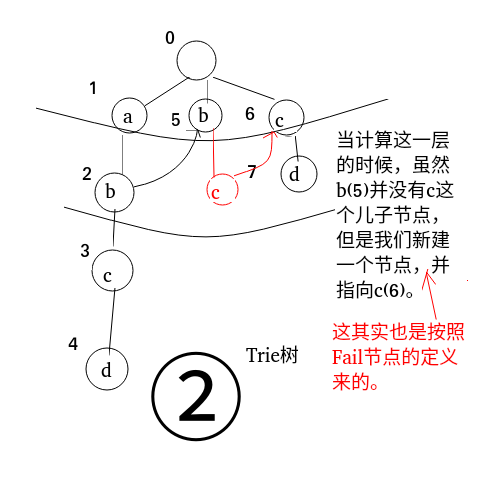
实际上是直接把 \(b(5)\) 的 儿子 \(c\) 当作 \(c(6)\)。
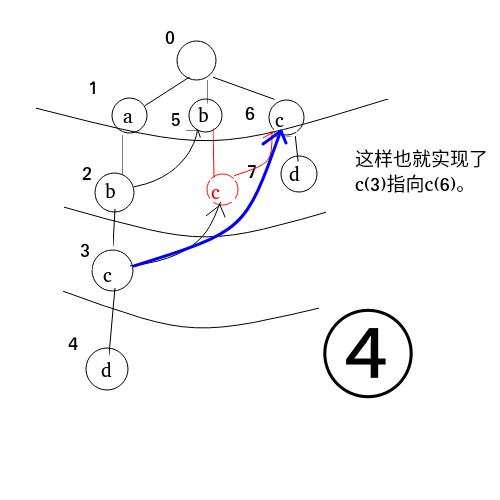
AC自动机的查找
查找只要在Trie树上遍历一遍字符串 \(T\),统计到 \(T_i\) 时,记得把 \(fail[T_i], fail[fail[T_i]], fail[fail[fail[T_i]]],\dots\) 都统计上。
例题
第一部分 模板题
P3808 【模板】AC 自动机(简单版)
本题纯模板
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1000010;
struct AhoCorasick { // AC自动机
int ch[N][26]; // Trie树
int fail[N]; // Fail指针
int val[N], idx; // 单词末尾标记(val) 以及 单词节点个数 (idx)
void insert(char s[]) { // Trie树的插入
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
if (!ch[p][u]) ch[p][u] = ++idx;
p = ch[p][u];
}
val[p]++;
}
void getfail() { // 计算fail指针
queue<int> q; // 采用BFS进行处理,所以要用到队列
for (int i = 0; i < 26; i++) {
if (ch[0][i]) { // 把第一层的节点插入队列
q.push(ch[0][i]);
}
}
while (q.size()) { //BFS
int t = q.front();
q.pop();
for (int i = 0; i < 26; i++) {
if (ch[t][i]) { // 如果t有i这个节点
fail[ch[t][i]] = ch[fail[t]][i]; // 那么Fail = “与父节点的Fail指针所指向的节点的与 x 同字符的子节点”
q.push(ch[t][i]); // 插入队列
}
else ch[t][i] = ch[fail[t]][i]; // 否则建立虚拟节点,也就是图中 c(3)连向 c(6)
}
}
}
int query(char s[]) {
int p = 0, ans = 0; // 当前节点(p)与答案(ans)
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
p = ch[p][u]; // 前往子节点
int v = p; // 统计v, fail[v], fail[fail[v]], ...
while (v && val[v] != -1) { // 统计v, fail[v], fail[fail[v]], ...
ans += val[v]; // 统计答案
val[v] = -1; // 避免重复统计
v = fail[v]; // 前往 fail[v]
}
}
return ans;
}
}ac;
int n;
char text[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> (text + 1);
ac.insert(text);
}
ac.getfail();
cin >> (text + 1);
cout << ac.query(text) << '\n';
return 0;
}
HDU2222 Keywords Search
本题纯模板
初始化时一定要初始化fail!!!
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
struct AhoCorasick {
int ch[N][26];
int val[N], idx;
int fail[N];
int q[N];
void init() {
memset(ch[0], 0, sizeof(ch[0]));
memset(fail, 0, sizeof(fail));
idx = 0;
}
void insert(char s[]) {
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
if (!ch[p][u]) {
ch[p][u] = ++idx;
memset(ch[idx], 0, sizeof(ch[idx]));
val[idx] = 0;
}
p = ch[p][u];
}
val[p]++;
}
void getfail() {
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++) {
if (ch[0][i]) {
q[++tt] = ch[0][i];
}
}
while (hh <= tt) {
int t = q[hh++];
for (int i = 0; i < 26; i++) {
if (ch[t][i]) {
fail[ch[t][i]] = ch[fail[t]][i];
q[++tt] = ch[t][i];
}
else ch[t][i] = ch[fail[t]][i];
}
}
}
int query(char s[]) {
int p = 0, ans = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
p = ch[p][u];
int v = p;
while (v && val[v] != -1) {
ans += val[v];
val[v] = -1;
v = fail[v];
}
}
return ans;
}
}ac;
char text[N];
void solve() {
int n;
cin >> n;
ac.init();
for (int i = 1; i <= n; i++) {
cin >> (text + 1);
ac.insert(text);
}
cin >> (text + 1);
ac.getfail();
cout << ac.query(text) << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P3796 【模板】AC 自动机(加强版)
本题只需要将 \(val[v] = -1\) 的标记去掉,再统计每一个单词的出现数量 \(cnt[u]\) 即可。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 80 * 160, M = 1000010;
struct AhoCorasick {
int ch[N][26];
int val[N], idx;
int fail[N];
int q[N]; // queue
int cnt[N]; // 记录每个串的出现次数
void init() {
memset(ch[0], 0, sizeof(ch[0]));
memset(fail, 0, sizeof(fail));
memset(cnt, 0, sizeof(cnt));
idx = 0;
}
void insert(char s[], int id) {
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
if (!ch[p][u]) {
ch[p][u] = ++idx;
memset(ch[idx], 0, sizeof(ch[idx]));
val[idx] = 0;
}
p = ch[p][u];
}
val[p] = id;
}
void getfail() {
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++) {
if (ch[0][i]) {
q[++tt] = ch[0][i];
}
}
while (hh <= tt) {
int t = q[hh++];
for (int i = 0; i < 26; i++) {
if (ch[t][i]) {
fail[ch[t][i]] = ch[fail[t]][i];
q[++tt] = ch[t][i];
}
else ch[t][i] = ch[fail[t]][i];
}
}
}
void query(char s[]) {
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
p = ch[p][u];
int v = p;
while (v) {
if (val[v]) cnt[val[v]]++;
v = fail[v];
}
}
}
}ac;
int n;
char text[M];
char tmp[160][80];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
while (cin >> n, n) {
ac.init();
for (int i = 1; i <= n; i++) {
cin >> (tmp[i] + 1);
ac.insert(tmp[i], i);
}
ac.getfail();
cin >> (text + 1);
ac.query(text);
int maxx = *max_element(ac.cnt + 1, ac.cnt + n + 1);
cout << maxx << '\n';
for (int i = 1; i <= n; i++) {
if (ac.cnt[i] == maxx) {
cout << tmp[i] + 1 << '\n';
}
}
}
return 0;
}
P5357 【模板】AC 自动机(二次加强版)
显然,一个一个统计会超时。
我们可以想到,当标记 \(p\) 时,\(fail[p],fail[fail[p]]\) 都会被标记,因此这里浪费了时间。
那我们可以使用树上差分的思想,本来是由 \(p\) 指向 \(fail[p]\), 现在改由 \(fail[p]\) 指向 \(p\),当匹配到节点 \(p\) 时,\(cnt[p] + 1\) 即可。
最后像树上差分一样自下而上地统计,因为 \(p\) 有的,\(fail[p]\) 也必须拥有。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 200010, M = 2000010;
int n;
char text[M];
struct Edge {
int to, next;
}e[N];
int head[N], idx;
void add(int a, int b) {
idx++, e[idx].to = b, e[idx].next = head[a], head[a] = idx;
}
struct AhoCorasick {
int ch[N][26];
int cnt[N];
int val[N], idx;
int fail[N];
int q[N];
void insert(char s[], int id) {
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
if (!ch[p][u]) ch[p][u] = ++idx;
p = ch[p][u];
}
val[id] = p;
}
void getfail() {
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++) {
if (ch[0][i]) {
q[++tt] = ch[0][i];
}
}
while (hh <= tt) {
int t = q[hh++];
for (int i = 0; i < 26; i++) {
if (ch[t][i]) {
fail[ch[t][i]] = ch[fail[t]][i];
q[++tt] = ch[t][i];
}
else ch[t][i] = ch[fail[t]][i];
}
}
for (int i = 1; i <= idx; i++) add(fail[i], i);
}
void query(char s[]) {
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'a';
p = ch[p][u];
cnt[p]++;
}
}
}ac;
void dfs(int u) {
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
dfs(to);
ac.cnt[u] += ac.cnt[to];
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> (text + 1);
ac.insert(text, i);
}
ac.getfail();
cin >> (text + 1);
ac.query(text);
dfs(0);
for (int i = 1; i <= n; i++) {
cout << ac.cnt[ac.val[i]] << '\n';
}
return 0;
}
第二部分 AC自动机与DP的结合
P4052 [JSOI2007]文本生成器
设 \(f_{i, j}\) 为枚举到第 \(i\) 个字符, 现在在Trie树上的第 \(j\) 个节点。
有$$f_{i + 1, trie_{j, c}} += f_{i, j}$$
表示由第 \(i\) 层的节点(实际上与枚举到第 \(i\) 个字符) \(c\) 转移到第 \(i + 1\) 层的节点 \(c\) 的儿子 \(trie_{j, c}\)。
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 6010, mod = 1e4 + 7;
struct AhoCorasick {
int ch[N][26];
int val[N], idx;
int fail[N], q[N];
bool can_read[N];
void insert(char s[]) {
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'A';
if (!ch[p][u]) ch[p][u] = ++idx;
p = ch[p][u];
}
val[p]++;
can_read[p] = true;
}
void getfail() {
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++) {
if (ch[0][i]) {
q[++tt] = ch[0][i];
}
}
while (hh <= tt) {
int t = q[hh++];
if (can_read[fail[t]]) can_read[t] = true;
for (int i = 0; i < 26; i++) {
if (ch[t][i]) {
fail[ch[t][i]] = ch[fail[t]][i];
q[++tt] = ch[t][i];
}
else ch[t][i] = ch[fail[t]][i];
}
}
}
}ac;
int n, m;
char text[N];
int f[110][N];
void dp() {
f[0][0] = 1;
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= ac.idx; j++) {
for (int k = 0; k < 26; k++) {
if (!ac.can_read[ac.ch[j][k]]) {
f[i + 1][ac.ch[j][k]] = (f[i + 1][ac.ch[j][k]] + f[i][j]) % mod;
}
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> (text + 1);
ac.insert(text);
}
ac.getfail();
dp();
int sum = 0, ans = 1;
for (int i = 1; i <= m; i++) ans = (ans * 26) % mod;
for (int i = 0; i <= ac.idx; i++) sum = (sum + f[m][i]) % mod;
cout << ((ans - sum) % mod + mod) % mod << '\n';
return 0;
}
P3041 [USACO12JAN]Video Game G
思路同上一题,使用 \(val[i]\) 记录第 \(i,fail[i],fail[fail[i]]\) 号节点作为单词末尾的数量。
那么有 $$f[i + 1][trie[j][c]] = \max({f[i][j]+val[trie[j][c]]})$$
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 400;
struct AhoCorasick {
int ch[N][3];
int val[N], idx;
int fail[N];
int q[N];
void insert(char s[]) {
int p = 0;
for (int i = 1; s[i]; i++) {
int u = s[i] - 'A';
if (!ch[p][u]) ch[p][u] = ++idx;
p = ch[p][u];
}
val[p]++;
}
void getfail() {
int hh = 0, tt = -1;
for (int i = 0; i < 3; i++) {
if (ch[0][i]) {
q[++tt] = ch[0][i];
}
}
while (hh <= tt) {
int t = q[hh++];
for (int i = 0; i < 3; i++) {
if (ch[t][i]) {
fail[ch[t][i]] = ch[fail[t]][i];
q[++tt] = ch[t][i];
}
else ch[t][i] = ch[fail[t]][i];
}
val[t] += val[fail[t]];
}
}
}ac;
int n, m;
char text[N];
int f[1010][N];
void dp() {
memset(f, 0xcf, sizeof(f));
for (int i = 0; i <= m; i++) f[i][0] = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j <= ac.idx; j++) {
for (int k = 0; k < 3; k++) {
f[i + 1][ac.ch[j][k]] = max(f[i + 1][ac.ch[j][k]], f[i][j] + ac.val[ac.ch[j][k]]);
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> (text + 1);
ac.insert(text);
}
ac.getfail();
dp();
int ans = 0;
for (int i = 0; i <= ac.idx; i++) ans = max(ans, f[m][i]);
cout << ans << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号