关于深度学习中卷积核操作
直接举例进行说明输出图片的长和宽。
输入照片为:32*32*3,
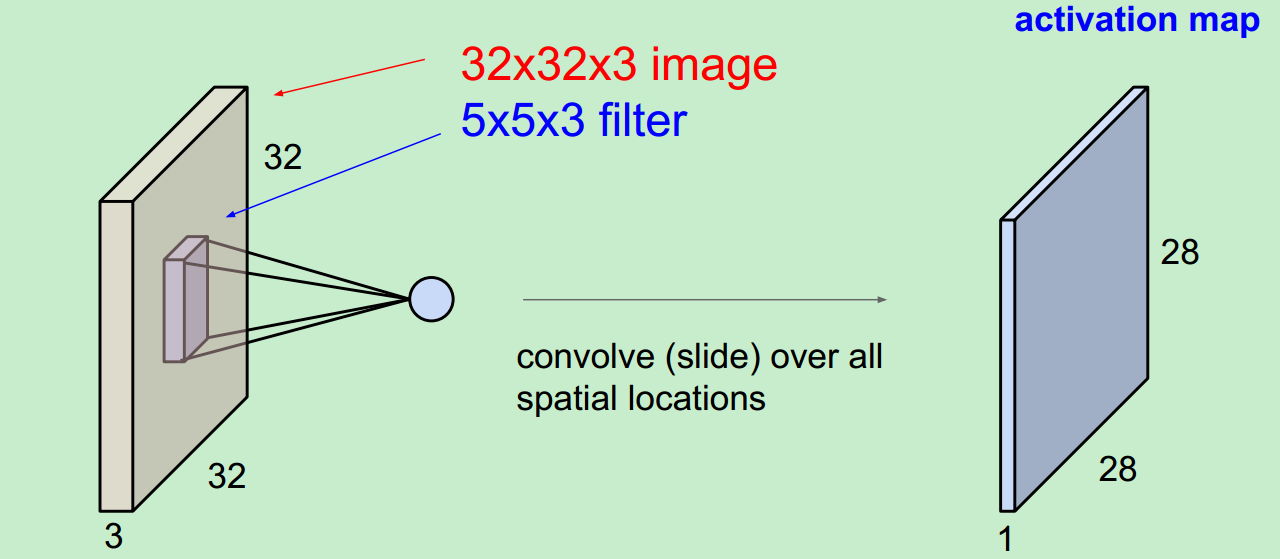
这是用一个Filter得到的结果,即使一个activation map。(filter 总会自动扩充到和输入照片一样的depth)。
当我们用6个5*5的Filter时,我们将会得到6个分开的activation maps,如图所示:
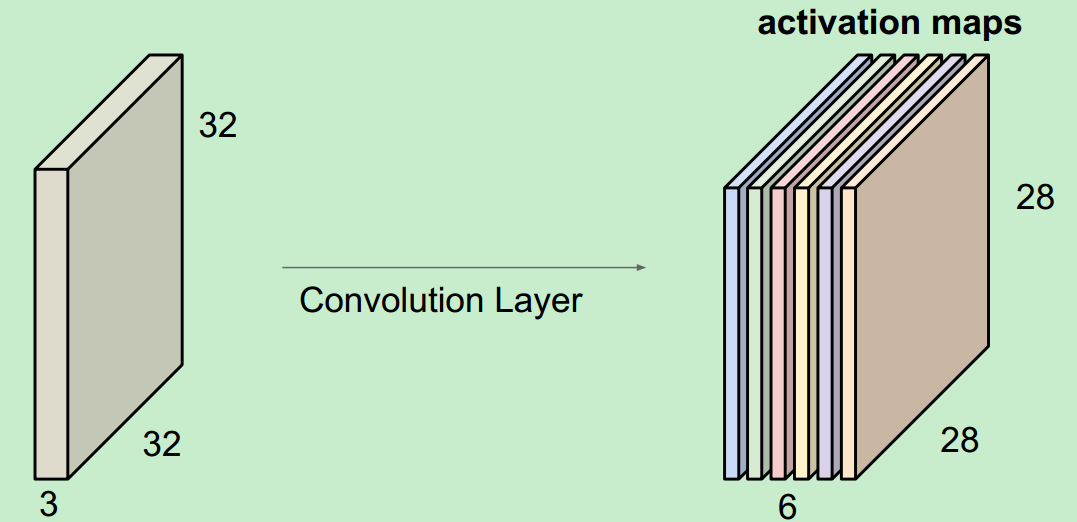
得到的“新照片”的大小为:28*28*6.
其实,每个卷积层之后都会跟一个相应的激活函数(activation functions):
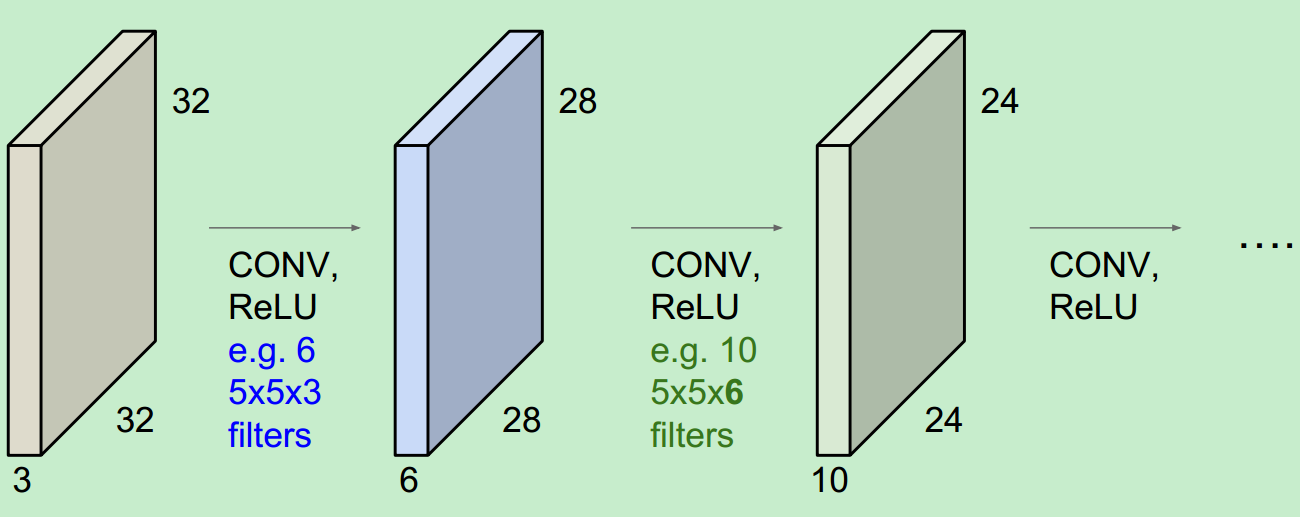
微观上,假设现在input为7*7,Filter尺寸为3*3,output过程如下所示:

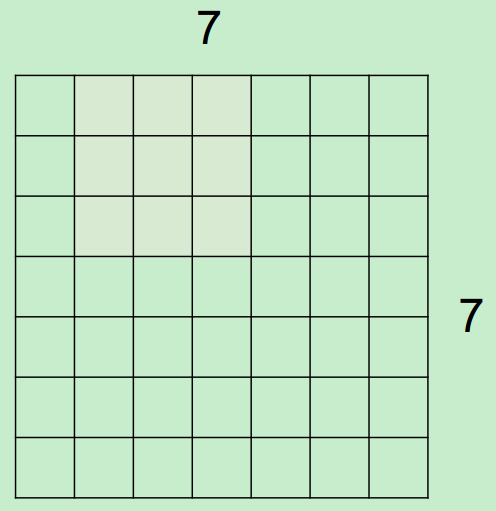
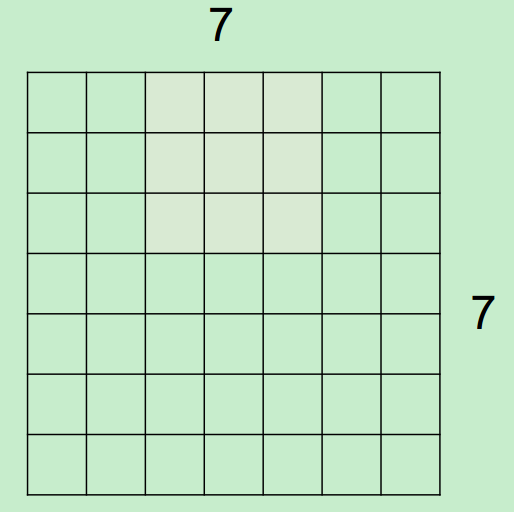
 最终得到一个5*5的output。
最终得到一个5*5的output。
假设,input为7*7,Filter尺寸为3*3,stride(步长)为2,则output过程如下所示:
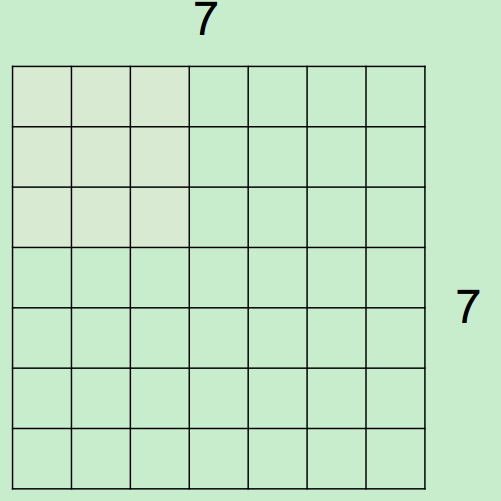
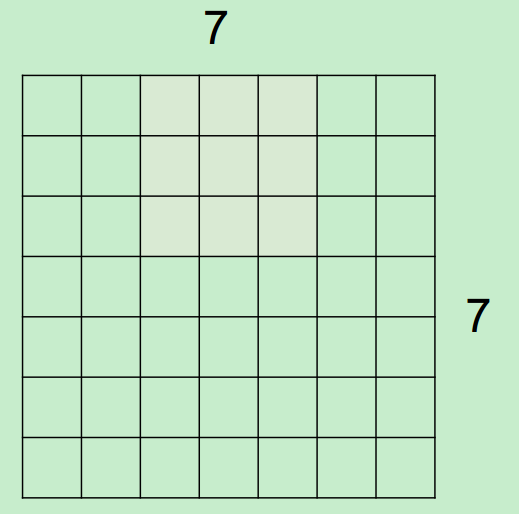
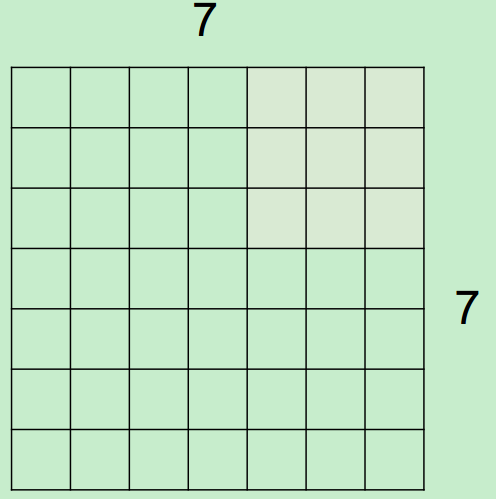 最终得到一个3*3的output。
最终得到一个3*3的output。
注:在这个例子中stride不能为3,因为那样就越界了。
总的来说
Output size=(N-F)/stride +1
当有填充(pad)时,例如对一个input为7*7进行pad=1填充,Filter为3*3,stride=1,会得到一个7*7的output。
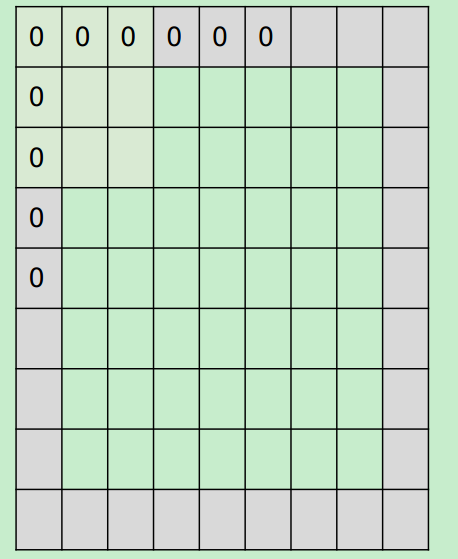
Output size=(N-F+2*pad)/stride +1
注:0填充(pad)的主要目的是因为我们在前面的图中所示的那样,一直用5*5的Filter进行卷积,会导致体积收缩的太快,不利于特征的提取。
举例说明:

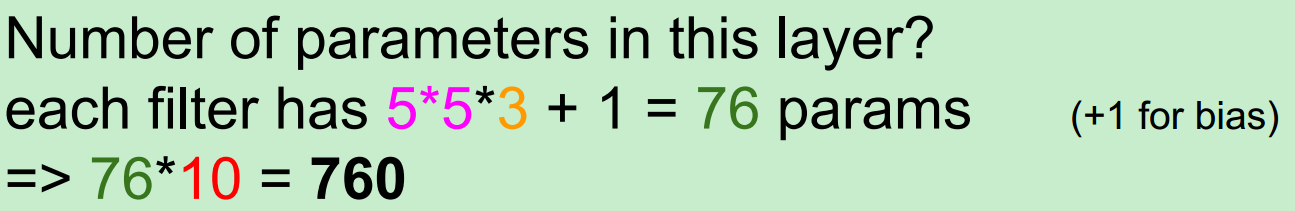
在这里要注意一下1*1的卷积核,为什么呢?
举例:一个56*56*64的input,用32个1*1的卷积核进行卷积(每一个卷积核的尺寸为1*1*64,执行64维的点乘操作),将得到一个56*56*32的output,看到输出的depth减少了,也就是降维,那么parameters也会相应的减少。
下面介绍一下Pooling(池化)操作:
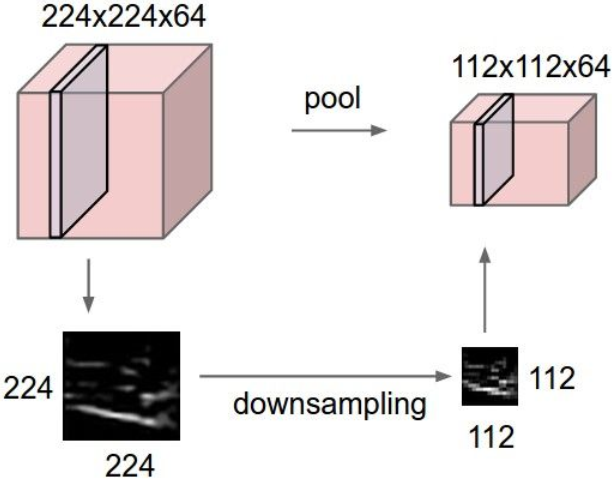
将represention变小,易于操作和控制,对每一个activation map单独进行操作。
用的最多的是最大池化(MAX POOLING):

Output size=(N-F)/S +1




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
· 三行代码完成国际化适配,妙~啊~