集合框架
Java集合
Java中存放数据工具主要分为两类:数组和集合。数组是单类型的,且使用它必须要声明它的容量,但是因为它是一个简单的线性序列,因此访问速度很快;而集合里面存放的是对象,可以存放任何东西,没有数量限制(实际上是根据策略透明扩容),但是这相对于数组在处理很多方面都有很大的便利。所以数组和集合他们各有便利。
数组:
首先是数组,数组可以通过Array进行创建,根据你创建的时机,决定是存储在栈中还是堆中还是系统内存中,在NIO中是通过nio包下的工具类来创建,可以在jvm中创建也可以在系统内存中创建。
集合框架:
然后是集合框架,集合框架实际上包含了两部分,Collection集合和Map映射,但是因为他们的功能都是为了有一个统一方便存储各种对象的工具,所以他们也都一起被称为集合。其本质上是一种Java定制的数据结构,它们的顶级结构,具体的实现细节由子类根据需求定制:
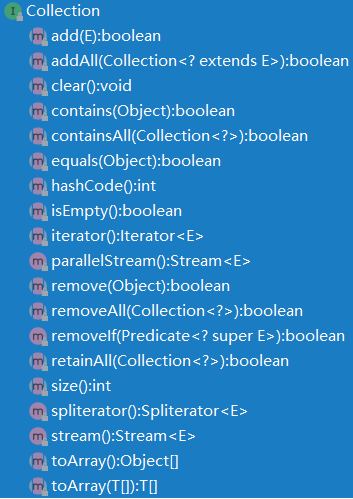
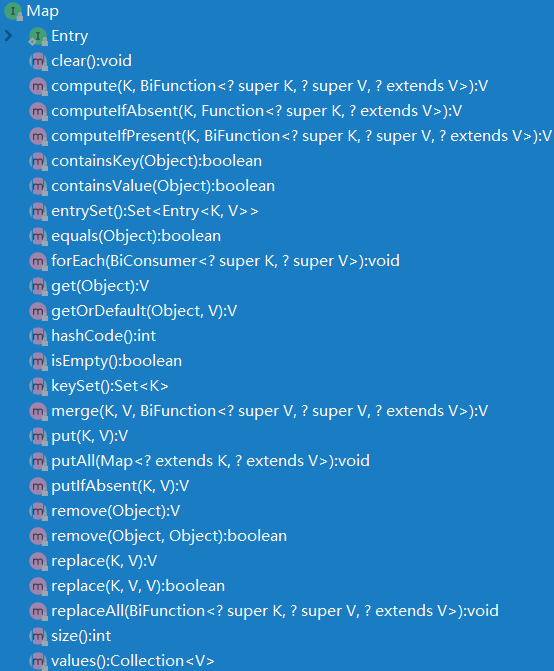
功能:Collection接口实现了Iterable接口,也就是它具备了迭代的功能。虽然Map没有实现Iterable接口,但是它的抽象子类间接拥有了这个接口的功能在public Set<K> keySet()和public Collection<V> values()方法中。
子类:Collection接口下面又有两个子接口,首先Collection接口中没有定义顺序功能,而它的子类List和Set继承了他的全部功能,但是List增加了顺序功能,所有List的子类必须维护这个顺序功能,具体怎么维护看选择方案。
实现:如ArrayList它继承自List,而Array意味着它的底层选择是数组(线性表)来实现这个顺序功能,并实现了get,indexof等定位顺序的方法,这些方法会提供顺序的支持。
而Set的子类无需实现顺序的功能,仅支持集合的功能即可,而具体怎么实现也看选择的底层是什么。
数据结构:Java底层的基本数据结构有线性表,栈,队列,链表,树。
线性表:最常用的、最简单的数据结构,它是n个数据元素的有限序列。实现线性表:输出存储线性表元素,即是用一组连续的存储单元,依次存储线性表数据元素,另一种是使用链表存储线性表元素,用一组任意的存储单元存储线性表的数据元素(存储单元可以连续,可以不连续)。
栈:先进后出。
队列:先进先出。
链表:物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表的指针地址实现,每个元素包含两个节点,一个是存储元素的数据域(存储空间),另外一个是指向下一个节点的指针域。根据指针的指向,链表形成不同的结构,例如单链表、双链表,循环链表
链表优点:不需要初始化容量,可以任意加减元素,添加或删除元素只需要改变前后两个元素节点的指针域指向地址即可,所以添加,删除很快
缺点:含有大量指针域,占用空间大,需要查找元素需要遍历链表来查找,比较耗时。
使用场景:数据量小,需要频繁增加,删除的操作。
树:一种数据结构,由n(n>=1)个有限节点组成的具有层级关系的集合。它看起来像倒挂的树,根朝上,叶朝下,具有以下特点:
1. 每个节点有零个或多个子节点
2. 没有父节点的节点是根节点
3. 每一个非根节有且只有一个父节点
4. 除了根节点,没格子节点可以分为多个不想交的子树。
5. 二叉树,是树中特殊的一种:
6. 每个节点最多有两颗子树,节点的度最多为2
7. 左子树和右子树是有顺序的,次序不能颠倒。
8. 即使某个节点只有一个子树,也要区分左右子树。
9. 二叉树是折中的方案,添加删除元素很快,在查找方面也有自己的算法优化,所以二叉树基友链表的好处,也有数组的好处,是两者的优化方法,在处理大批量动态数据方面非常有用。
拓展:平衡二叉树、红黑树。B+树等。这些数据结构二叉树的基础上衍生了很多功能,在实际应用中广泛用到,例如Mysql索引结构用的是B+树,还有HashMap底层源码是红黑树
所以集合的实现类就是以各种基本数据结构实现的特定集合类。
List的子类有:LinkedList;ArrayList;Vector。
LinkedList:双向链表;ArrayList线性表;Vector和ArrayList类似只是数据操作方法都是同步的。
Set的子类有:HashSet;TreeSet;LinkedHashSet。
HashSet:就是hashMap的key;TreeSet:就是treeMap;LinkedHashSet:就是连接起来的Hashset。
Map的子类有:HashMap;HashTable;LinkedHashMap;TreeMap;ConcurrentHashMap。
HashMap:HashMap是基于Hash表实现的,它的实现细节是Node,而Node实现了Map.Entry,Node被均匀的散列分布在数组中构成了HashMap的hash表,用Node节点来提供Map映射的支持,实际的情况比这个要复杂,为了解决Hash冲突,HashMap在1.8之前采用的是链表+桶的方式,因为链表会导致get的效率从o(1)降至o(n),所以在1.8之后就采用了红黑树(自平衡二叉查找树)+链表+数组的方式。但是HashMap这种追求极致效率为目的的Hash表就注定了它无法承受大量的数据,因为平衡无处不在,效率和耐力只能二选一。
HashTable:也是基于Hash表实现的,但它定义了自己的Entry,并在属性声明上和HashMap一致,Entry.setValue方法要求Value不能为空,另外HashTable实现了Dictionary接口,
1 * The <code>Dictionary</code> class is the abstract parent of any 2 * class, such as <code>Hashtable</code>, which maps keys to values. 3 * Every key and every value is an object. In any one <tt>Dictionary</tt> 4 * object, every key is associated with at most one value. Given a 5 * <tt>Dictionary</tt> and a key, the associated element can be looked up. 6 * Any non-<code>null</code> object can be used as a key and as a value. 7 * <p> 8 * As a rule, the <code>equals</code> method should be used by 9 * implementations of this class to decide if two keys are the same. 10 * <p> 11 * <strong>NOTE: This class is obsolete. New implementations should 12 * implement the Map interface, rather than extending this class.</strong>
上面是Dictionary接口的Doc,可以看出Dictionary接口的约束就是key和value不能为空,且每个key必须对应一个value,另外这个类是过时的。所以HashTable也是Dictionary的子类,受其约束。与HashMap最大的差异就是这货是线程安全的,另外扩容倍数和再hash算法不同,解决冲突的方法仍然是链表+桶,所以虽然它是线程安全的但是在解决hash冲突上效率不高,也就导致了同步资源过久,加剧激烈的竞争,任何系统中都可能存在资源阻塞被无限放大的可能,最终导致了系统的崩溃。but we has the concurrentHashMap now,it is better。
LinkedHashMap:继承了HashMao的同时,自己的Entry也继承了HashMap的Node,同时在自己的Entry类中新增了before和after属性,所以它的Key-value是自带顺序的Hash表,当我们迭代它的元素时,我们存的时候怎么存它就原样按序输出(因为我们存的时候他们每个元素是知道前后地址的)。所以这货就是HashMap,只是再加工了下定义了自己输出有序的功能,但是使用时需要考虑到维护有序的顺序是耗费资源的这个现实问题。
TreeMap:LinkedHashMap实现了输出有序,好了现在我们不需要你输出有序了,给我一个无论使用多久都能保证查询效率是一个稳定增长的常数,而不是一个指数增长的常数(比如1.8以前的HashMap,一旦链表崩溃(长度过长),那么它的查找速度还不如数组,即从O1升级到了On),即现在需要的是一个每次数据变动都会让自己的数据结构自平衡到最佳状态的Hash表,它的实现方案是采用红黑树作为基础。
ConcurrentHashMap:ConcurrentHashMap实现了自己的Node,而不是继承HashMap的。
***************************************************************************************************************
红黑树:
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
一棵深度为k,且有2^k-1个结点的二叉树,称为满二叉树。这种树的特点是每一层上的结点数都是最大结点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且或者最后一层是满的,或者是在右边缺少连续若干结点,则此二叉树为完全二叉树。具有n个结点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树,至少有2k-1个叶子结点,至多有2k-1个结点。二叉树只是定义了一棵基本的树,最原始的树。二叉树的实现使用了递归算法,递归算法这里讲的很好:https://blog.csdn.net/feizaosyuacm/article/details/54919389;二叉树这里:https://www.jianshu.com/p/bf73c8d50dc2
二叉堆是一种特殊的堆,二叉堆是完全二元树(二叉树)或者是近似完全二元树(二叉树)。二叉堆有两种:最大堆和最小堆。最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值
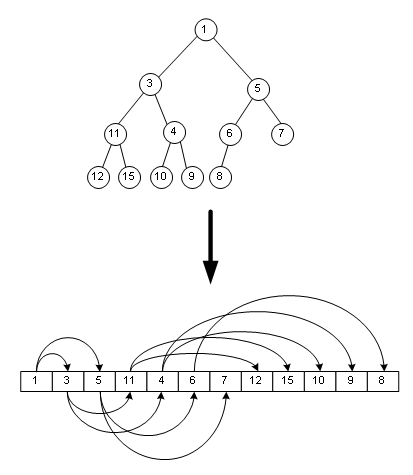
二叉堆一般都通过"数组"来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。我们将"二叉堆的第一个元素"放在数组索引0的位置。
假设"第一个元素"在数组中的索引为 0 的话,则父节点和子节点的位置关系如下:
1、索引为i的左孩子的索引是 (2*i+1);
2、索引为i的右孩子的索引是 (2*i+2);
3、索引为i的父结点的索引是 floor((i-1)/2);
二叉堆这种有序队列如何入队呢?
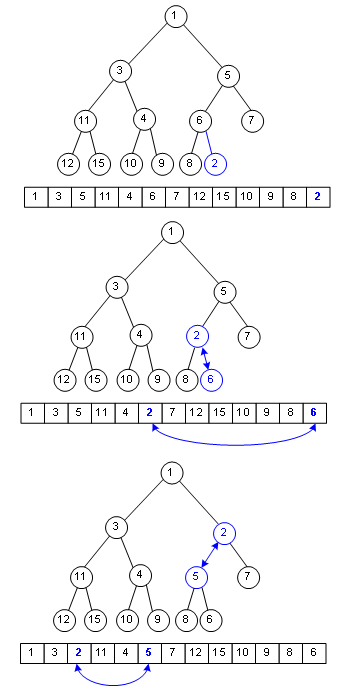
假设要在这个二叉堆里入队一个单元,只要在数组末尾加入这个元素,然后把这个元素往上挪,直到挪不动,经过了这种复杂度为Ο(logn)的操作,二叉堆性质没有变化。
那如何出队呢?
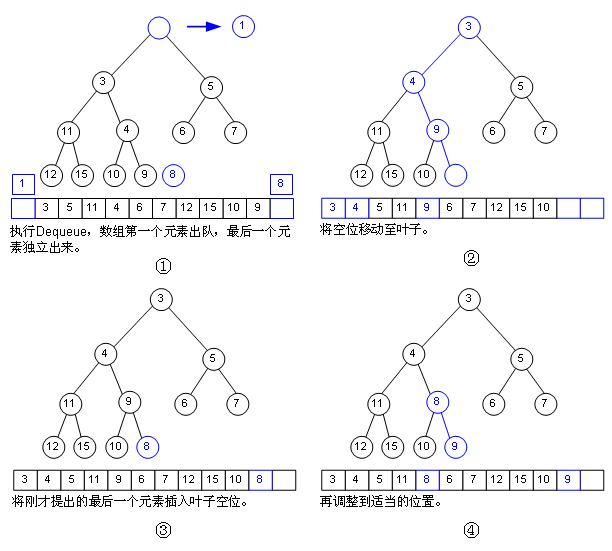
我们习惯将二叉堆画成树的形式,但本质上还是用数组实现的。二叉堆这里:https://www.cnblogs.com/zhangbaochong/p/5188288.html
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。像这样:
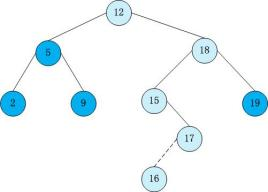
AVL树:在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树,AVL来自它的发明者名字的缩写 --百度百科
红黑树是一种自平衡二叉树,是在计算机科学中使用的一种数据结构,典型的用途是实现关联数组。红黑树是一种特化的AVL树,红黑树是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。 --百度百科
红黑树的删除和增加都需要堆树进行旋转如左旋和右旋,来保持上面5个性质的稳定。
HashMap中使用到了红黑树结构:
1. 首先看HashMap的Node结构:
1 static class Node<K,V> implements Map.Entry<K,V> 2 final int hash; 3 final K key; 4 V value; 5 Node<K,V> next;
2. 然后是HashMap的属性:
初始容量:1 << 4;最大容量:1<< 30;加载因子0.75f;链表进化为红黑树阈值:8;红黑树退化为链表阈值:6;树化时最小表容量:64(树化或扩充表的阈值)
3. 接下来是方法:
3.1. 定位算法:就是怎么根据hashCode的值获得其在HashMap中的数组的索引,这里以get为例:
1 final Node<K,V> getNode(int hash, Object key) { 2 Node<K,V>[] tab; Node<K,V> first, e; int n; K k; 3 if ((tab = table) != null && (n = tab.length) > 0 && 4 (first = tab[(n - 1) & hash]) != null) { 5 if (first.hash == hash && // always check first node 6 ((k = first.key) == key || (key != null && key.equals(k)))) 7 return first; 8 if ((e = first.next) != null) { 9 if (first instanceof TreeNode) 10 return ((TreeNode<K,V>)first).getTreeNode(hash, key); 11 do { 12 if (e.hash == hash && 13 ((k = e.key) == key || (key != null && key.equals(k)))) 14 return e; 15 } while ((e = e.next) != null); 16 } 17 } 18 return null; 19 }
看到上面标红的了吗,这就是老版的indexfor方法,为了让hahsCode的值均匀的分布在数组中,我们让hashcode对数组长度-1做取模运算,因为取模运算可以快速的低消耗的计算出hash在数组中的位置,那为什么是n-1&hash呢?
这是因为偶数的二进制最后一位是0,0与任何数与都是0,而hashMap的数组长度是偶数的,所以拿着hashMap的长度直接与上hashCode会导致无法辨别末尾的值,就是1111和1110的hashcode会产生hash冲突然后被存到了链表,而链表的增删改查的效率都是On而数组的效率是O1,所以避免形成链表是hash函数的意义。另外所有二进制末尾是1的index位置永远都不会被使用,本来hash表最重要的就是hash槽,现在又有一些位置永远不会被使用,omg。
3.2. hash哈希算法:
1 static final int hash(Object key) { 2 int h; 3 return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); 4 }
如果key是空的那么hash后的index是0,这就解释了为什么hashmap可以存放一个null的原因了,key为null时自动被存放到了index=0的位置。然后就是hash算法,这个地方很有意思:拿着key的hashCode异或上key的hashCode无符号右移3位的值。
有意思就有意思在这个h>>>16地方,这个函数在这里是一个扰动函数,我们知道一个二进制数有32位,高16位右移变成低16位,那么这个二进制数的高16位全部变为0,0和任何数异或都是0,这样做的目的是什么呢?我们先考虑这样一个问题,我们使用hash表的原因是什么?当然是为了hash表理想状态下的O1效率的CRUD,但是因为hash冲突的原因,这种理想状态,很难实现,但是我们可以改善这种状态,怎么改善呢?自然是尽量让每个元素的hashCode都有它全部元素的特性。
我们已经知道了在定位算法中hashCode需要与的值是hash表的长度减1,这是个奇数,奇数的二进制是什么样呢?高位为0,低位为1,再想另外一个问题,0与任何数与都是0,所以在表长度不大的情况下,表长度减1的高16位基本全部为0,所以key的hashCode的高16位就废了,怎么办呢?让hashCode的高16位和自己的低16位在低16位的位置进行异或,这样自己的低16位就是高16位和低16位的结合,会变的更散列,而高16位因为与0进行异或不变,所以即使hash表的size很大,也会保证这高16位在后续可以参与到定位算法的运算中。所以这就是扰动函数的功能,使整个key的hashCode的二进制每一位都参与到定位算法的运算中,从而减少hash冲突的发生几率。
3.3. 存取方法:
3.3.1上面的getNode方法就是hashMap的取方法,除了总是先判断是否是第一个元素外,没有什么特殊的处理。
3.3.2下面是put方法,细节还算明朗:
1 final V putVal(int hash, K key, V value, boolean onlyIfAbsent, 2 boolean evict) { 3 Node<K,V>[] tab; Node<K,V> p; int n, i; 4 if ((tab = table) == null || (n = tab.length) == 0) #判断是否未初始化 5 n = (tab = resize()).length;#初始化 6 if ((p = tab[i = (n - 1) & hash]) == null)#是否hsah位置没有被占 7 tab[i] = newNode(hash, key, value, null);#直接存入 8 else {#hash位置被占 9 Node<K,V> e; K k; 10 if (p.hash == hash && 11 ((k = p.key) == key || (key != null && key.equals(k))))#如果hash位置的数组的元素中的key与传入的key相等直接覆盖 12 e = p;#覆盖 13 else if (p instanceof TreeNode)#里面存的是一颗红黑树 14 e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);#。。。此处是红黑树的自平衡 15 else {#里面存得是一个链表 16 for (int binCount = 0; ; ++binCount) { 17 if ((e = p.next) == null) { 18 p.next = newNode(hash, key, value, null); 19 if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st 20 treeifyBin(tab, hash); 21 break; 22 } 23 if (e.hash == hash && 24 ((k = e.key) == key || (key != null && key.equals(k)))) 25 break; 26 p = e; 27 } 28 } 29 if (e != null) { // existing mapping for key 30 V oldValue = e.value; 31 if (!onlyIfAbsent || oldValue == null) 32 e.value = value; 33 afterNodeAccess(e); 34 return oldValue; 35 } 36 } 37 ++modCount; 38 if (++size > threshold) 39 resize(); 40 afterNodeInsertion(evict); 41 return null; 42 }
3.3.3接着是resize方法(因为1.8牵扯到了红黑树,所以较复杂):
1 final Node<K,V>[] resize() { 2 Node<K,V>[] oldTab = table;#复制一个临时表 3 int oldCap = (oldTab == null) ? 0 : oldTab.length;#获得数组的长度 4 int oldThr = threshold;#得到本次扩充的长度 5 int newCap, newThr = 0;#定义新长度和下一次扩充的长度 6 if (oldCap > 0) { 7 if (oldCap >= MAXIMUM_CAPACITY) {#是否超过了最大长度,如果超过了就不再扩充并返回原数组 8 threshold = Integer.MAX_VALUE; 9 return oldTab; 10 } 11 else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && 12 oldCap >= DEFAULT_INITIAL_CAPACITY)#没有超过 下次扩充长度位本次新长度的double 13 newThr = oldThr << 1; // double threshold 14 } 15 else if (oldThr > 0) // initial capacity was placed in threshold 16 newCap = oldThr; 17 else { // zero initial threshold signifies using defaults 18 newCap = DEFAULT_INITIAL_CAPACITY; 19 newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); 20 } 21 if (newThr == 0) { 22 float ft = (float)newCap * loadFactor; 23 newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? 24 (int)ft : Integer.MAX_VALUE); 25 } 26 threshold = newThr; 27 @SuppressWarnings({"rawtypes","unchecked"}) 28 Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];#从此处开始,新建一个新长度的数组 29 table = newTab;#这一步我是着实没看懂啊 30 if (oldTab != null) { 31 for (int j = 0; j < oldCap; ++j) {#开始遍历老数组 32 Node<K,V> e; 33 if ((e = oldTab[j]) != null) {#如果这个数组的j位置有数据,开始迁移这个数据,迁移到e 34 oldTab[j] = null;#首先把这个数组j位置清除 35 if (e.next == null)#如果e是一个单Node 36 newTab[e.hash & (newCap - 1)] = e;#重新计算hash然后存到新的数组中 37 else if (e instanceof TreeNode)#如果e是个红黑树 38 ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);#这里是红黑树的构建 39 else {#如果是个链表 // preserve order 40 Node<K,V> loHead = null, loTail = null; 41 Node<K,V> hiHead = null, hiTail = null; 42 Node<K,V> next; 43 do { 44 next = e.next; 45 if ((e.hash & oldCap) == 0) { 46 if (loTail == null) 47 loHead = e; 48 else 49 loTail.next = e; 50 loTail = e; 51 } 52 else { 53 if (hiTail == null) 54 hiHead = e; 55 else 56 hiTail.next = e; 57 hiTail = e; 58 } 59 } while ((e = next) != null); 60 if (loTail != null) { 61 loTail.next = null; 62 newTab[j] = loHead; 63 } 64 if (hiTail != null) { 65 hiTail.next = null; 66 newTab[j + oldCap] = hiHead; 67 } 68 } 69 } 70 } 71 } 72 return newTab; 73 }
在如果是链表的位置,我看了别人的讲解感觉完全看不懂,但是自己总算是想明白了这堆代码在搞什么,画板画的太麻烦了,就把手稿传上来了:

所以,A一直在Head手里,而这里面的e每次少一个前置节点,少的那个节点都被放在了A的后面,然后逐渐遍历完整个链表,每个元素都被转移到了LoHead上面,且是按照原本链表的顺序。这也是JDK8和之前的版本HashMap的不同,因为之前版本的链表倒置会出现死循环的问题,在1.8也修复了,但是因为HashMap没有采取任何同步手段,所以并发情况下仍然不可以使用,因为其又产生了其他的并发问题。
3.3.4 红黑树的构建
1 final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) { 2 TreeNode<K,V> b = this;#定义一个树节点 3 // Relink into lo and hi lists, preserving order 4 TreeNode<K,V> loHead = null, loTail = null; 5 TreeNode<K,V> hiHead = null, hiTail = null; 6 int lc = 0, hc = 0; 7 for (TreeNode<K,V> e = b, next; e != null; e = next) { 8 next = (TreeNode<K,V>)e.next; 9 e.next = null; 10 if ((e.hash & bit) == 0) { 11 if ((e.prev = loTail) == null) 12 loHead = e; 13 else 14 loTail.next = e; 15 loTail = e; 16 ++lc; 17 } 18 else { 19 if ((e.prev = hiTail) == null) 20 hiHead = e; 21 else 22 hiTail.next = e; 23 hiTail = e; 24 ++hc; 25 } 26 } 27 28 if (loHead != null) { 29 if (lc <= UNTREEIFY_THRESHOLD) 30 tab[index] = loHead.untreeify(map); 31 else { 32 tab[index] = loHead; 33 if (hiHead != null) // (else is already treeified) 34 loHead.treeify(tab); 35 } 36 } 37 if (hiHead != null) { 38 if (hc <= UNTREEIFY_THRESHOLD) 39 tab[index + bit] = hiHead.untreeify(map); 40 else { 41 tab[index + bit] = hiHead; 42 if (loHead != null) 43 hiHead.treeify(tab); 44 } 45 } 46 }
好吧,这个和resize是一样的原理,这里就不再赘述了,需要说明的是LoHead和HiHead的区别:
1 /** 2 * Initializes or doubles table size. If null, allocates in 3 * accord with initial capacity target held in field threshold. 4 * Otherwise, because we are using power-of-two expansion, the 5 * elements from each bin must either stay at same index, or move 6 * with a power of two offset in the new table. 7 * 8 * @return the table 9 */
上图是resize的文档说明:因为扩充是oldcap*2,所以每个桶的元素要么在原本的索引位置,要么在oldcap+原本位置的索引值的索引位置。这也就是LoHead和HiHead的由来,我一直以为是低头LoHead和低尾LoTail,但是看情况并不是这么直译的,LoHead代表索引为未变动,HiHead代表索引位置变成了原本索引位置+oldcap。
本来要写下红黑树的具体内容的,太长了放弃了,后面有时间再补充。
concurrenthashmap是分段锁的hash表,表中的元素和hashmap一样也是链表+红黑树,只不过concurretnhashmap有多个hash表,分别锁定,分别操作。源码有时间再仔细研究。



