LOJ #3341. 「NOI2020」时代的眼泪
看题解不要在多个题解之间反复横跳！
题目叙述
平面上若干个点 \((i,p_i)\) ，其中 \(p_i\) 为一个 \(1\sim n\) 的排列，\(m\) 次询问，每次询问一个矩形内部点对满足一个在左下一个在右上的数量。
题解
分块
直接分块。
散块对整块/散块的贡献
预处理 \(s_{i,j}\) 表示 \(1\sim i\) 这些块内，值 \(\le j\) 的数的数量。
每次枚举散块里面的点，差分即可。有的时候做分块要暴力一点，有人做这个部分的时候用的是离线然后在一个值域分块里面每次添加一个数，查询值在一个区间内的数的数量。
散块内部/整块内部
考虑将每个整块离散化，预处理处 \(s_{i,j}\) 表示这个散块 \(i\) 往前，\(\le j\) 数的数量。
然后每次询问直接二分一下什么的，\(\mathcal O(\sqrt{n})\) 复杂度查询一个散块就可以了。
整块内部也是类似的，因为只有 \(\mathcal O(n)\) 种本质不同的情况，直接预处理答案就可以了。
整块之间
考虑容斥，假设需要计算块构成的区间 \([l,r]\) 在值域 \([d,u]\) 内的逆序对数量。
那么直接转化为 \([l,r]\) 内在 \([1,u]\) 内的逆序对数两减去 \([l,r]\) 内在 \([1,d-1]\) 内的逆序对数再减去小的在 \([l,r],[1,d-1]\) ，大的在 \([l,r],[d,u]\) 的数量。
- 前面相当于求形如 \([l,r]\) ，值域在 \([1,i]\) 的逆序对数量。这个可以考虑从小到大添加每一个数。相当于对这个数所在的块添加一个最大的数。那么贡献就是前面所有比这个数小的数的数量，这个可以通过我们计算散块预处理出来的东西计算他。这是每次修改需要做的事情，如果把第 \(x\) 个块对第 \(y\) 个块的贡献放在第 \(x\) 行 \(y\) 列，修改相当于修改一列，询问的时候枚举哪个块在后面，相当于查询一行之和，需要处理一下前缀和。
- 后面这个，计算出每个块内值域在 \([1,d-1]\) 的数量有多少个，做一个前缀和，再枚举每个块查询值域在 \([d,u]\) 内的数的数量，与他前面在 \([1,d-1]\) 内的数的数量相乘，加起来就好了。
感觉这种题就很没意思。给我5h应该是可以做出来的。
树套树
先树套树。线段树套动态开点线段树。
考虑在树套树划分出来的方块中统计答案。
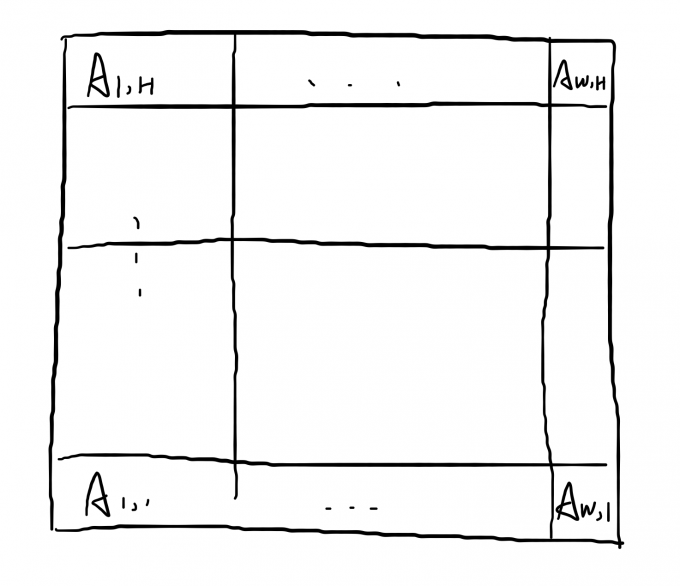
每个小方块代表树套树上的一个区间。
贡献可以拆分为若干部分。
- 两个方块不同行不同列产生的贡献。这个可以直接在树套树上统计。
- 两个方块同行/同列产生的贡献。那么就相当于一个矩形产生的贡献。但是这个矩形一定满足行/列的区间都在树套数上出现过。
- 这样会算重。因为同行/同列会把交叉的部分内部的顺序对多算一次，所以减去。
1，3直接在树套数上统计。2可以发现这是若干个区间顺序对问题，并且每个区间都是线段树上出现过的区间，因此直接每个线段树上的节点再开一个用来查询区间逆序对的东西就可以了（因为这样的东西需要的复杂度/空间是和区间内数的数量相关的，所以不会复杂度过高，写的时候也可以把这个东西挂到线段树上然后离线莫队）。
总结
- 分块题不要忘记一个块的大小只有 \(\sqrt{n}\) ，所以其实如果是至于区间询问的话只有 \(\mathcal O(n)\) 种。
- 有时候分治完了再分块会产生意想不到的效果。
代码
不是我的，是FZzzz的。
#include<algorithm>
#include<vector>
#include<cmath>
#include<cstdio>
#include<cctype>
using namespace std;
inline int readint(){
int x=0;
char c=getchar();
bool f=0;
while(!isdigit(c)&&c!='-') c=getchar();
if(c=='-'){
f=1;
c=getchar();
}
while(isdigit(c)){
x=x*10+c-'0';
c=getchar();
}
return f?-x:x;
}
const int maxn=1e5+5,maxm=2e5+5,maxS=350,maxB=350;
int n,m,p[maxn],p2[maxn];
int S,B,L[maxB],R[maxB],pos[maxn];
int ord[maxn],s1[maxB][maxn],s2[maxB][maxS][maxS];
int lbd[maxB][maxn],ubd[maxB][maxn],s3[maxB][maxS][maxS];
bool cmp(int a,int b){
return p[a]<p[b];
}
typedef long long ll;
ll ans[maxm];
int query1(int r1,int r2,int c1,int c2){
return s1[r2][c2]-s1[r1-1][c2]-s1[r2][c1-1]+s1[r1-1][c1-1];
}
int query2(int x,int r1,int r2,int c1,int c2){
return s2[x][r2][c2]-s2[x][r1-1][c2]-s2[x][r2][c1-1]+s2[x][r1-1][c1-1];
}
int query(int r1,int r2,int c1,int c2){
int x=pos[r1];
ll ans=0;
for(int i=L[x];i<=R[x];i++)
if(r1<=ord[i]&&ord[i]<=r2&&c1<=p[ord[i]]&&p[ord[i]]<=c2)
ans+=query2(x,lbd[x][c1],i-L[x],r1-L[x]+1,ord[i]-L[x]);
return ans;
}
struct qry{
int l,r,id;
bool flag;
qry(int l,int r,int id,bool flag):l(l),r(r),id(id),flag(flag){}
};
vector<qry> q[maxn];
ll s4[maxB][maxB];
ll query4(int l,int r){
ll ans=0;
for(int i=l;i<=r;i++) ans+=s4[i][r]-s4[i][l-1];
return ans;
}
int main(){
#ifdef LOCAL
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
n=readint();
m=readint();
for(int i=1;i<=n;i++) p2[p[i]=readint()]=i;
S=sqrt(n);
B=(n-1)/S+1;
for(int i=1;i<=B;i++){
L[i]=(i-1)*S+1;
R[i]=i==B?n:i*S;
for(int j=L[i];j<=R[i];j++){
pos[j]=i;
s1[i][p[j]]++;
ord[j]=j;
}
sort(ord+L[i],ord+R[i]+1,cmp);
for(int j=1;j<=n;j++) s1[i][j]+=s1[i-1][j]+s1[i][j-1]-s1[i-1][j-1];
for(int j=L[i];j<=R[i];j++) s2[i][j-L[i]+1][ord[j]-L[i]+1]=1;
for(int j=1;j<=R[i]-L[i]+1;j++) for(int k=1;k<=R[i]-L[i]+1;k++)
s2[i][j][k]+=s2[i][j-1][k]+s2[i][j][k-1]-s2[i][j-1][k-1];
for(int j=1;j<=p[ord[L[i]]];j++) lbd[i][j]=1;
for(int j=L[i];j<R[i];j++)
for(int k=p[ord[j]]+1;k<=p[ord[j+1]];k++) lbd[i][k]=j-L[i]+2;
for(int j=p[ord[R[i]]]+1;j<=n;j++) lbd[i][j]=R[i]-L[i]+2;
for(int j=1;j<p[ord[L[i]]];j++) ubd[i][j]=1;
for(int j=L[i];j<R[i];j++)
for(int k=p[ord[j]];k<p[ord[j+1]];k++) ubd[i][k]=j-L[i]+2;
for(int j=p[ord[R[i]]];j<=n;j++) ubd[i][j]=R[i]-L[i]+2;
for(int j=1;j<=R[i]-L[i]+1;j++) for(int k=j;k<=R[i]-L[i]+1;k++)
s3[i][j][k]=s3[i][j][k-1]+query2(i,j,k-1,1,ord[L[i]+k-1]-L[i]);
}
for(int i=0;i<m;i++){
int r1,r2,c1,c2;
r1=readint();
r2=readint();
c1=readint();
c2=readint();
if(pos[r1]==pos[r2]){
ans[i]=query(r1,r2,c1,c2);
continue;
}
ans[i]=query(r1,R[pos[r1]],c1,c2)+query(L[pos[r2]],r2,c1,c2);
vector<int> res1,res2;
for(int j=L[pos[r1]];j<=R[pos[r1]];j++)
if(ord[j]>=r1&&c1<=p[ord[j]]&&p[ord[j]]<=c2)
res1.push_back(p[ord[j]]);
for(int j=L[pos[r2]];j<=R[pos[r2]];j++)
if(ord[j]<=r2&&c1<=p[ord[j]]&&p[ord[j]]<=c2)
res2.push_back(p[ord[j]]);
int cur=0;
for(int j=0;j<(int)res1.size();j++){
while(cur<(int)res2.size()&&res2[cur]<res1[j]) cur++;
ans[i]+=res2.size()-cur;
}
for(int j=r1;j<=R[pos[r1]];j++) if(c1<=p[j]&&p[j]<=c2)
ans[i]+=query1(pos[r1]+1,pos[r2]-1,p[j]+1,c2);
for(int j=L[pos[r2]];j<=r2;j++) if(c1<=p[j]&&p[j]<=c2)
ans[i]+=query1(pos[r1]+1,pos[r2]-1,c1,p[j]-1);
for(int j=pos[r1]+1;j<pos[r2];j++)
ans[i]-=1ll*query1(j,j,1,c1-1)*query1(j+1,pos[r2]-1,c1,c2);
for(int j=pos[r1]+1;j<pos[r2];j++)
ans[i]+=s3[j][lbd[j][c1]][ubd[j][c2]-1];
q[c2].push_back(qry(pos[r1]+1,pos[r2]-1,i,1));
q[c1-1].push_back(qry(pos[r1]+1,pos[r2]-1,i,0));
}
for(int i=1;i<=n;i++){
for(int j=1;j<pos[p2[i]];j++) s4[pos[p2[i]]][j]+=query1(1,j,1,i-1);
for(int j=pos[p2[i]];j<=B;j++)
s4[pos[p2[i]]][j]+=query1(1,pos[p2[i]]-1,1,i-1);
for(int j=0;j<(int)q[i].size();j++)
if(q[i][j].flag) ans[q[i][j].id]+=query4(q[i][j].l,q[i][j].r);
else ans[q[i][j].id]-=query4(q[i][j].l,q[i][j].r);
}
for(int i=0;i<m;i++) printf("%lld\n",ans[i]);
return 0;
}
树套树（也不是我的）：
#include <bits/stdc++.h>
#define mid ((l + r) >> 1)
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
const int M = 2e5 + 5;
int read() {
int x = 0, ch = getchar();
while (ch < '0' || ch > '9') ch = getchar();
while ('0' <= ch && ch <= '9') x = 10*x + ch - '0', ch = getchar();
return x;
}
ll res[M];
int a[2][N], n, m, block, ql[2][M], qr[2][M];
struct Q {
int l, r, i;
Q(){}
Q(int ll, int rr, int ii) {l = ll, r = rr, i = ii;}
};
vector<int> qry[N<<2];
void addq(int o, int p, int l, int r, int id) {
if (ql[o][id] <= l && r <= qr[o][id]) return qry[p].push_back(id), void();
if (ql[o][id] <= mid) addq(o, p << 1, l, mid, id);
if (qr[o][id] > mid) addq(o, p << 1 | 1, mid + 1, r, id);
}
namespace tree_tree{
const int S = N*20;
int rt[N<<2], tot, siz[S], ls[S], rs[S], sum[M][38];
ll t[S], tmp[38], cnt;
void modify(int &p, int l, int r, int x) {
if (!p) p = ++tot; siz[p] = 1;
if (l == r) return ;
x <= mid ? modify(ls[p], l, mid, x) : modify(rs[p], mid+1, r, x);
}
void merge(int &p, int q) {
if (!p || !q) return p += q, void();
t[p] += t[q] + (ll)siz[ls[p]] * siz[rs[q]] - t[ls[p]] - t[rs[p]] - t[ls[q]] - t[rs[q]];
siz[p] += siz[q];
merge(ls[p], ls[q]);
merge(rs[p], rs[q]);
t[p] += t[ls[p]] + t[rs[p]];
}
void query(int p, int l, int r, int id) {
if (ql[1][id] <= l && r <= qr[1][id]) {
res[id] -= t[p];
tmp[++cnt] = siz[p];
return ;
}
if (ql[1][id] <= mid) query(ls[p], l, mid, id);
if (qr[1][id] > mid) query(rs[p], mid + 1, r, id);
}
void solve(int p, int l, int r) {
if (l == r) modify(rt[p], 1, n, a[0][l]);
else {
solve(p << 1, l, mid);
solve(p << 1 | 1, mid + 1, r);
merge(rt[p << 1], rt[p << 1 | 1]), rt[p] = rt[p << 1];
}
for (auto id : qry[p]) {
cnt = 0, query(rt[p], 1, n, id);
for (int i = 1, j = 0; i <= cnt; i++) {
res[id] += (ll)tmp[i] * j;
j += sum[id][i], sum[id][i] += tmp[i];
}
}
}
}
namespace block_sum{
int L[N], R[N], pos[N], tag[N], sum[N], n;
void build(int num, int b) {
n = num;
for (int i=1;;i++) {
L[i] = R[i-1] + 1;
R[i] = min(R[i-1] + b, n);
for (int j=L[i];j<=R[i];j++) pos[j] = i, sum[j] = 0;
tag[i] = 0;
if (R[i] == n) break;
}
}
void update(int x) {
for(int i=x;i<=R[pos[x]];i++) sum[i]++;
for(int i=pos[x]+1;i<=pos[n];i++) tag[i]++;
}
int gsum(int x) {return sum[x] + tag[pos[x]];}
}
bool cmp(const Q &a, const Q &b) {
int p = a.l / block, q = b.l / block;
return (p == q ? ((p & 1) ? a.r < b.r : a.r > b.r) : a.l < b.l);
}
vector<Q> vec[N]; ll ans[M], pre[M];
pair<int, int> qc[M][2];
inline int sgn(int x) {return x>0?1:-1;}
void get_answer(int *a, Q *q, int n, int m) {
if (n == 1 || !m) return ;
block = (int)ceil(sqrt(0.7 * n * n / m)), sort(q + 1, q + m + 1, cmp);
block_sum::build(n, (int)sqrt(n));
for(int i=0;i<=n;i++) vec[i].clear();
for(int i=1,l=1,r=0;i<=m;i++) {
ans[i] = 0;
qc[i][0] = {r, q[i].r};
qc[i][1] = {q[i].l - 1, l - 1};
if (r < q[i].r) vec[l-1].emplace_back(r+1, q[i].r, -i), r = q[i].r;
if (l > q[i].l) vec[r].emplace_back(q[i].l, l-1, -i);
while (l > q[i].l) l--, ans[i] += r-l+1;
if (r > q[i].r) vec[l-1].emplace_back(q[i].r+1, r, i), r = q[i].r;
if (l < q[i].l) vec[r].emplace_back(l, q[i].l-1, i);
while (l < q[i].l) ans[i] -= r-l+1, l++;
}
for(int i=1;i<=n;i++) {
pre[i] = pre[i - 1] + block_sum::gsum(a[i]), block_sum::update(a[i]);
for (auto k : vec[i]) for(int j=k.l;j<=k.r;j++) {
ans[abs(k.i)] += sgn(k.i) * block_sum::gsum(a[j]);
}
}
for(int i=1;i<=m;i++) {
ans[i] += ans[i-1];
ans[i] += pre[qc[i][0].second] - pre[qc[i][0].first];
ans[i] += pre[qc[i][1].second] - pre[qc[i][1].first];
res[q[i].i] += ans[i];
}
}
namespace segtree{
Q q[M]; int v[N];
void solve(int o, int p, int l, int r) {
int as = 0, qs = 0;
for(int i=l;i<=r;i++) v[++as] = a[o][i];
sort(v + 1, v + as + 1);
for (auto id : qry[p]) {
int L = lower_bound(v + 1, v + as + 1, ql[!o][id]) - v;
int R = upper_bound(v + 1, v + as + 1, qr[!o][id]) - v - 1;
if (L < R) q[++qs] = (Q){L, R, id};
}
for(int i=1;i<=as;i++) v[i] = a[!o][v[i]] - l + 1;
get_answer(v, q, as, qs);
if (l == r) return;
solve(o, p << 1, l, mid);
solve(o, p << 1 | 1, mid + 1, r);
}
};
int main() {
freopen("tears.in", "r", stdin);
freopen("tears.out", "w", stdout);
n = read(), m = read();
for(int i=1;i<=n;i++) a[0][i] = read(), a[1][a[0][i]] = i;
for(int i=1;i<=m;i++) {
ql[0][i] = read(), qr[0][i] = read();
ql[1][i] = read(), qr[1][i] = read();
addq(0, 1, 1, n, i);
}
tree_tree::solve(1, 1, n);
segtree::solve(0, 1, 1, n);
for (int i=1;i<=4*n;i++) qry[i].clear();
for (int i=1;i<=m;i++) addq(1, 1, 1, n, i);
segtree::solve(1, 1, 1, n);
for(int i=1;i<=m;i++) printf("%lld\n", res[i]);
return 0;
}
