LOJ #2306. 「NOI2017」蔬菜
本文大部分内容转述自command_block
题目叙述
\(n\) 种蔬菜，每种蔬菜有一个价格 \(A_i\) 和腐烂程度 \(X_i\) ，第一次卖这种菜会得到 \(S_i\) 的收益，库存 \(C_i\) 。现在有若干天卖东西，每天第 \(i\) 种蔬菜会腐烂掉 \(X_i\) 个。注意，这是对每一个蔬菜来说的，如果把那些在第 \(i\) 天腐烂掉的蔬菜卖出去，剩下的蔬菜是不会腐烂的。每天最多卖 \(m\) 个蔬菜，问卖 \(q_i\) 天的情况下，最大收益是多少。一共有 \(k\) 组询问。
\(m\le 10\) 。
题解
首先考虑时间倒流。蔬菜腐烂，并不好处理，但是如果是增加，就可以增量处理了。
问题转化为每天每种蔬菜各加入一些。一种直觉上的选法是选择价值最大的 \(m\) 棵蔬菜把他们都卖掉。事实上，这样做就是正确的。一棵菜不论是现在卖还是以后再卖，都会被卖掉。而且以后回有更好的菜加入，说不定就没空卖现在这个菜了。所以，现在最优的 \(m\) 棵菜就是要卖掉。
多次询问怎么办。考虑一个更强的结论：\(t-1\) 天最优卖菜的一种情况会是 \(t\) 天卖菜的某种最优情况的子集。
考虑反证，如果不是最优的。那么 \(t\) 天在前 \(t-1\) 天的最优卖菜方案也不是最优的，因为前 \(t-1\) 天的最优卖菜方案可以替代 \(t\) 天的前 \(t-1\) 天的最优情况。有人说，可能 \(t-1\) 的最优卖菜方案会导致第 \(t\) 天的方案就没有办法按照原本的方式卖了，我说可以通过调整顺序避免这件事情，说明还是 \(t-1\) 天的最优方案有不在 \(t\) 天方案的子集内的操作，这样就完全可以替换。
所以做法是先按照开始的最优策略得到每种菜最终卖了多少个（在整体最优方案里），然后再将每棵菜的价值从大到小排序，选择在前面的若干棵卖掉就可以了。
但是贪心做法还是很神秘，尽量还是模拟费用流。一种做法是这样的：
考虑一种建图方法，源点向每天的每种菜连边，每天的菜向限制每天总卖出量的节点连边（这里还是时光倒流，菜变为添加），限制卖出量的节点向汇点连边。
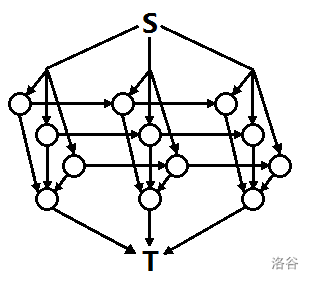
考虑 “增量-最大费用任意流” ，就是说最大费用最大流可以通过这样一种方式来实现：每次添加一个节点，通过添加经过这个节点的源点到汇点的边权和为正的路径，还有从汇点出发回到汇点的正权环，来完成最大费用任意流。
每次考虑经过新加入的节点的流和正权环。所有正权环必然经过源点，因为所有有边权的边都是从源点出发的。然而所有经过源点的环都不如直接走源点到汇点的路径，因为路径和环对源点到汇点路径的影响都是流量减少 1 。
这样可以发现，任意路径都不会从汇点退流。这就导出了一个结论是 \(p-1\) 天的卖菜方案是 \(p\) 天的子集。
然后维护菜的堆，模拟费用流模拟出 \(10^5\) 天的状态，最后再把每棵菜的收益排序，前 \(p\) 天把 \(pm\) 棵菜都卖掉就是最优情况了。
注意，看command_block的图，一定不要以为线段的交点也代表一个节点！！如果这样理解会发现有一些更多的经过反向边的情况！！！
总结
- “增量-最大费用任意流”模型。
- 对蔬菜的减少一定要敏感，转化为增加更容易处理。
