[NOI2002] 荒岛野人

Description

克里特岛以野人群居而著称。岛上有排列成环行的M个山洞。这些山洞顺时针编号为1,2,…,M。岛上住着N个野人，一开始依次住在山洞C1,C2,…,CN中，以后每年，第i个野人会沿顺时针向前走Pi个洞住下来。

每个野人i有一个寿命值Li，即生存的年数。

下面四幅图描述了一个有6个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为1，2，3；每年要走过的洞穴数依次为3，7，2；寿命值依次为4，3，1。

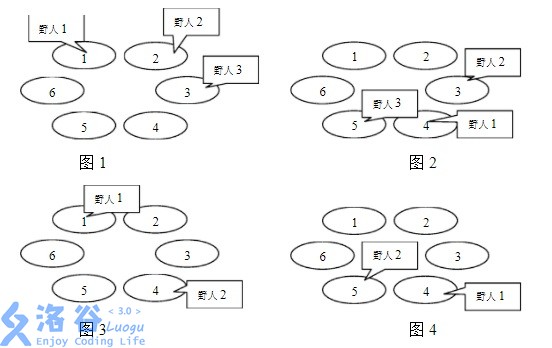
奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

Input

第1行为一个整数N(1<=N<=15)，即野人的数目。

第2行到第N+1每行为三个整数Ci, Pi, Li (1<=Ci,Pi<=100, 0<=Li<=106 )，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

Output

仅包含一个数M，即最少可能的山洞数。输入数据保证有解，且M不大于10^6。

Solution

注意到答案不大于 \(10^6\)，考虑从小到大枚举答案。

对于枚举的一个答案 \(ans\)，我们希望对于每个满足 \(c_i+k\times p_i\equiv c_j+k\times p_j\;(mod\;ans)\) 的 \(k\) ,都要 \(k>\min(l[i],l[j])\)。

于是可以 \(\mathcal {O(n^2)}\) 的枚举点对判断。

如何判断呢？再推一下式子：

\[c_i+k\times p_i=c_j+k\times p_j+m\times ans \]

\[k\times(p_i-p_j)+m\times ans=c_j-c_i \]

于是式子就愉快的变成了 \(exgcd\) 标准形式。

然后求 \(k\) 就好了。

ps：注意如果无解并不代表不满足情况，反而是满足情况。因为无解就是这俩货这辈子都碰不上面，显然合法。

Code

#include<cstdio>
#include<cctype>
#define N 20
#define min(A,B) ((A)<(B)?(A):(B))
#define max(A,B) ((A)>(B)?(A):(B))

int n;
int c[N],p[N],l[N];

int exgcd(int a,int b,int &x,int &y){
	if(!b){
		x=1;y=0;
		return a;
	}
	int d=exgcd(b,a%b,x,y);
	int t=x;
	x=y;
	y=t-a/b*y;
	return d;
}

signed main(){
	scanf("%d",&n);int mx=0;
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&c[i],&p[i],&l[i]);
		mx=max(mx,c[i]);
	}
	for(int ans=mx;;ans++){
		bool flag=0;
		for(int i=1;i<=n;i++){
			for(int j=i+1;j<=n;j++){
				int x,y;
				int k=p[i]-p[j]; k=(k%ans+ans)%ans;
				int g=exgcd(k,ans,x,y);
				if((c[j]-c[i])%g)
					continue;
				x*=(c[j]-c[i])/g;
				int mo=ans/g;
				x=(x%mo+mo)%mo;
				if(x<=min(l[i],l[j])){
					flag=1;
					break;
				}
			}
			if(flag)
				break;
		}
		if(flag)
			continue;
		printf("%d",ans);
		return 0;
	}
}