[总结] 后缀数组学习笔记

\[emmm$ 又开了字符串的新坑，下一个阶段大概就是学习后缀家族吧... ~~没有~~紧跟机房里神仙的步伐 先学后缀数组好了 # 概念 参考博客-> [戳我戳我](https://xminh.github.io/2018/02/27/%E5%90%8E%E7%BC%80%E6%95%B0%E7%BB%84-%E6%9C%80%E8%AF%A6%E7%BB%86(maybe)%E8%AE%B2%E8%A7%A3.html) 求出来SA数组就看了我半天... 放一个板子自己感觉难理解的东西都在注释里了 ```cpp #include<set> #include<map> #include<cmath> #include<queue> #include<cctype> #include<vector> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using std::min; using std::max; using std::swap; using std::vector; typedef double db; typedef long long ll; #define pb(A) push_back(A) #define pii std::pair<int,int> #define all(A) A.begin(),A.end() #define mp(A,B) std::make_pair(A,B) namespace NewweN{ const int N=1e6+5; int x[N],y[N],c[N]; char s[N];int n,m,num,sa[N]; char buf[1048578];int ptr,MX; char nc(){ if(ptr==MX) MX=fread(buf,1,1<<20,stdin),ptr=0; return ptr==MX?EOF:buf[ptr++]; } #define getchar nc int getint(){ int X=0,w=0;char ch=getchar(); while(!isdigit(ch))w|=ch=='-',ch=getchar(); while( isdigit(ch))X=X*10+ch-48,ch=getchar(); if(w) return -X;return X; } void getsa(){ m=122; for(int i=1;i<=n;i++) x[i]=s[i],c[x[i]]++; for(int i=2;i<=m;i++) c[i]+=c[i-1]; for(int i=n;i;i--) sa[c[x[i]]--]=i; for(int k=1;num=0,k<=n;k<<=1){ for(int i=n-k+1;i<=n;i++) y[++num]=i; for(int i=1;i<=n;i++) if(sa[i]>k) y[++num]=sa[i]-k; //y[i]->第二关键字排名为i的是第几个后缀 for(int i=1;i<=m;i++) c[i]=0; for(int i=1;i<=n;i++) c[x[i]]++; //x[i]->第i个后缀的第一关键字排名是多少 for(int i=2;i<=m;i++) c[i]+=c[i-1]; for(int i=n;i;i--) sa[c[x[y[i]]]--]=y[i],y[i]=0; //双关键字的基数排序 推荐洛谷日报的那篇 for(int i=1;i<=n;i++) swap(x[i],y[i]); x[sa[1]]=1;num=1; for(int i=2;i<=n;i++) x[sa[i]]=(y[sa[i]]==y[sa[i-1]] and y[sa[i]+k]==y[sa[i-1]+k])?num:++num; //因为之前交换过了x,y数组所以这里的y实际上是上一次的x if(num==n) return; m=num; } } signed main(){ scanf("%s",s+1); n=strlen(s+1); getsa(); for(int i=1;i<=n;i++)printf("%d ",sa[i]); return 0; } } int yzh=NewweN::main(); signed main(){return 0;} ``` 然而这只是最基础的一步... SA最重要的东西应该是Height数组 height[i] 表示 LCP(i,i-1) 其中 LCP(x,y) 为 suff(sa[x]) 和 suff(sa[y]) 的最长公共前缀。 简单的说 height[i] 就是排名为 i 的后缀与排名为 i-1 的后缀最长公共前缀 然后怎么求 height 直接引用那篇博客里的证明了: > 设h[i]=height[rk[i]]，同样的，height[i]=h[sa[i]]; > > 那么现在来证明最关键的一条定理： > > h[i]>=h[i-1]-1; > > 首先我们不妨设第i-1个字符串按排名来的前面的那个字符串是第k个字符串，注意k不一定是i-2，因为第k个字符串是按字典序排名来的i-1前面那个，并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。 > > 这时，依据height[]的定义，第k个字符串和第i-1个字符串的公共前缀自然是height[rk[i-1]]，现在先讨论一下第k+1个字符串和第i个字符串的关系。 > > 第一种情况，第k个字符串和第i-1个字符串的首字符不同，那么第k+1个字符串的排名既可能在i的前面，也可能在i的后面，但没有关系，因为height[rk[i-1]]就是0了呀，那么无论height[rk[i]]是多少都会有height[rk[i]]>=height[rk[i-1]]-1，也就是h[i]>=h[i-1]-1。 > > 第二种情况，第k个字符串和第i-1个字符串的首字符相同，那么由于第k+1个字符串就是第k个字符串去掉首字符得到的，第i个字符串也是第i-1个字符串去掉首字符得到的，那么显然第k+1个字符串要排在第i个字符串前面。同时，第k个字符串和第i-1个字符串的最长公共前缀是height[rk[i-1]]， > > 那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rk[i-1]]-1。 > > 到此为止，第二种情况的证明还没有完，我们可以试想一下，对于比第i个字符串的排名更靠前的那些字符串，谁和第i个字符串的相似度最高（这里说的相似度是指最长公共前缀的长度）？显然是排名紧邻第i个字符串的那个字符串了呀，即sa[rank[i]-1]。但是我们前面求得，有一个排在i前面的字符串k+1，LCP(rk[i],rk[k+1])=height[rk[i-1]]-1; > > 又因为height[rk[i]]=LCP(i,i-1)>=LCP(i,k+1) > > 所以height[rk[i]]>=height[rk[i-1]]-1，也即h[i]>=h[i-1]-1。 于是就可以 $O(n)$ 求出 h (即height[rk]) 数组了 ```cpp void getheight(int k=0){ for(int i=1;i<=n;i++) rk[sa[i]]=i; for(int i=1;i<=n;i++){ if(rk[i]==1) continue; if(k) --k; int j=sa[rk[i]-1]; while(i+k<=n and j+k<=n and s[i+k]==s[j+k]) k++; height[rk[i]]=k; } } ``` 后缀数组的所有东西大概都是在 height 数组上乱搞吧... # 例题 ## [洛谷P2408 不同子串个数] ### 题意 给定长度为n的字符串，求本质不同的子串个数。 ### Sol [链接](https://www.luogu.org/problemnew/show/P2408) **子串是所有后缀的所有前缀** 考虑每个后缀贡献的前缀个数，即排名为i的后缀的贡献为n-sa[i]+1-height[i] 用所有的前缀个数，减去与上一个排名的相同前缀个数（即LCP）。 证明大概就是，从没出现过的前缀一定不会在LCP中统计到，出现过的前缀一定在上一个中出现过（因为这里是排名上的相邻）。 ## [洛谷2852 牛奶模式] ### 题意 给定 n 个值域在 [0,1000000] 的整数，请求出最长的出现了至少 k 次的子串。 ### Sol [链接](https://www.luogu.org/problemnew/show/P2852) **子串是所有后缀的前缀** 可以二分一个 mid ，然后判断是否有某个长度 >=mid 的子串出现了 k 次及以上 那怎么用height快速求是否有子串出现了k次以上呢？ 因为height[i]表示的是LCP(i,i-1) 所以如果有一个子串出现好多次的话那一定是连续一段后缀的前缀（这里连续一段后缀是指排过序之后的后缀）具体可以反证法证明。 于是这题就二分答案之后扫一遍是否有连续k个height都>=mid就行了 ## [SDOI2008 Sandy的卡片] ### 题意 给定n个数字序列，每个数字序列长为len_i，要求找出最大的k，满足这n个序列都具有长为k的相同子串。子串相同定义为：长度相同且一个串的所有元素加上一个数会变成另一个串。数字序列总长度<=10^6。 ### Sol 如果做过[这道题](http://poj.org/problem?id=1743)的话做法就比较显然了 ~~哦这题我RE了两个小时然后弃了~~ 首先可以求出每个数字序列的差分序列然后去掉第一项，最后求出来答案加上1就好了。 原因是如果差分序列的连续x项相等的话在原序列里就是x+1项相等了。但是如果包含第一项的话差分序列就不固定了所以要把首项去掉。 之后可以把这n个数字序列连在一起，中间加上分隔符隔开就好。 然后就可以求出SA然后二分，每次看连续一段>=mid的height是否包含了n个数字序列，如果包含说明mid合法。 ## [HDU3518 Boring couting] ### 题意 求不重叠地出现至少两次的本质不同的子串个数。n<=1000。 ### Sol 数据范围可以 O(n^2) 做 先求出SA，然后枚举长度len，扫一遍height数组分段。如果一段内的端点之差>=len，那么表示找到了一个新的合法串,ans++。 ## [SDOI2016 生成魔咒] ### 题意 最开始有一个空串，要进行n次操作每次操作都会在当前串之后加一个字符。要求输出每次操作之后当前串的所有本质不同子串个数。n<=10^5 ### Sol 还是挺水的吧... 因为我们在刷sa题所以可以想到先把这n个字符读完跑一遍sa。 因为长度为n的本质不同的子串个数就是n*(n+1)/2-height[]。考虑每次删去一个字符动态维护height。 但是如果每次删除末尾的一个字符的话我们的sa数组和rk数组是会变化的，，，但是删除开头的字符不会！ 于是可以反过来做这题，就是说每次往末尾加一个字符变成往开头加一个字符！这样就可以支持每次删除开头字符了。然后再随便拿链表维护一下rk[]的前驱和后继再拿st表求最小值就可以AC啦！ ## [HAOI2016 找相同字符] ### 题意 给定两个字符串，求出在两个字符串中各取出一个子串使得这两个子串相同的方案数。两个方案不同当且仅当这两个子串中有一个位置不同。n1,n2<=2*10^5 ### Sol ~~文化课上想OI题真是爽~~ 首先可以将两个串中间加个'~'连起来跑一遍SA，这样就有了个O(n^2)的做法，分别枚举两个子串的开头位置i和j，然后ans+=lcp(height[i+1]...height[j])。 有了这个式子还是比较容易搞成线性的，因为height数组的值肯定是大到小再大到小再再大到小.. 而两个后缀的lcp就是字典序排序后夹在他们中间的最小的height。 这样，我们就可以用单调栈维护这个最小值同时维护答案。分A串的子串在前、B的子串在前两种情况分别用单调栈求出答案，加起来就行。 ## [SPOJ687 REPEATS] ### 题意 给定字符串，求重复最多的子串重复次数。n<=50000 ### Sol ~~哈哈哈哈哈学考终于考完了！！~~ 一道论文题 有个性质就是如果长度为len的子串出现了两次或更多，记这个串为S，那S肯定包含了s[len],s[len\*2],s[len\*3]...中的某相邻两个。我们把这些点看作关键点，那么只需要看字符s[i\*len]和s[(i+1)\*len]向前向后最远能匹配到多远记为K，那这里就是连续出现了K/L+1次。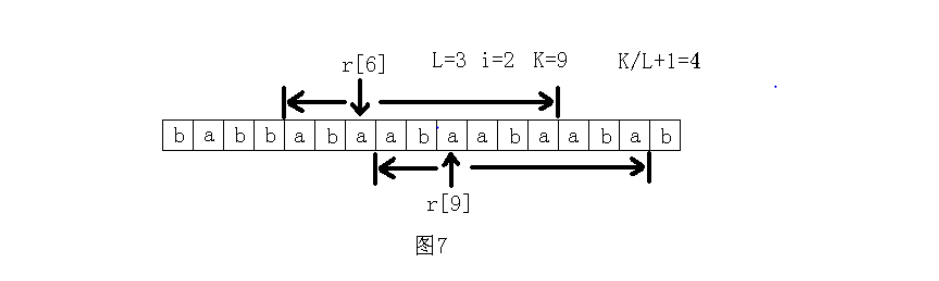 这里有张论文里piao来的图 其中len=3,i=2（他的数组从0开始标号差评  嗯这样就很清晰了 因为调和级数的性质，所以这里的时间复杂度为O(nlogn) ## [NOI2016 优秀的拆分] ### 题意 如果一个字符串可以被拆分成形如AABB的形式，就称作该拆分为优秀的拆分。其中A，B均为非空子串。给定一个字符串S，请求出S的所有子串的所有拆分方式中，优秀拆分的总个数。T<=10,n<=30000。 ### Sol 首先可以转换一下求两个数组a[i],b[i]表示分别以i为结尾/开头的字符，'AA'的形式有多少个。那么答案就是∑b[i-1]\*a[i]。 然后问题就转化为给定一个字符串，求以每个位置为开头，'AA'的形式有多少个。 如果做过上面那道论文题的话还是会对'放置关键点'这个操作比较熟练的吧 具体就是枚举长度len，然后枚举'AA'经过的关键点i,i+len 我们求出i,i+len的最长公共前缀x和最长公共后缀y，如果x+y>len，那么‘AA'串一定存在 于是就要对[i-y+1,i+x-len+1]的a数组区间加1 b数组类似 但是这样会造成重复统计，所以需要把x,y分别与len取min，这样就可以保证不重不漏啦 ## [BZOJ2119 股市的预测] ### 题意 给定长度为 $N$ 的数组，问有多少个形如 $ABA$ 的串，其中 $B$ 的长度是给定值 $m$，$A$ 的长度大于 $0$ 。$N\leq 50000$ ### Sol 还是挺水的 这种找连续出现的相同的串的话都要用到‘放置关键点’的思想 具体可以枚举 $A$ 的长度 $len$，每隔 $len$ 设置一个关键点，那前后两个 $A$ 一定分别经过两个关键点。枚举第一个 $A$ 经过的哪个关键点设为 $l$ ，那在第二个 $A$ 中对应的位置就是 $l+m+len$ 。找出以这两个点为端点的 $lcs,lcp$ 长度，如果 $\ge len$ 就更新答案。\]