激活函数综述

目录

• 前言
• Sigmoid型函数
  • logistic函数
  • tanh函数
• ReLu相关函数
  • ReLU激活函数
  • LeakyReLU函数
  • PReLU函数
  • ELU函数
  • Softplus函数
• Swish函数和GLEU函数
  • Swish函数
  • GELU函数
• Maxout单元

前言

激活函数，是神经网络中实现非线性计算的关键，再深的线性神经网络，本质上都和单步线性计算等价。所以，激活函数这个非线性单元是神经网络化腐朽为神奇的关键。

激活函数的要求：

1. 计算简单，特别是导函数计算简单
2. 连续可导（允许在若干个点上不可导）
3. 值域合理，这样可以尽量使得不同网络层的输入和输出数据相似

Sigmoid型函数

sigmoid型函数是一类S型曲线函数，两端饱和。

logistic函数

logistic激活函数是一个左右饱和的激活函数，将输入压缩到(0, 1)的区间中。

\[logistic(x) = \frac{1}{1+e^{-x}} \]

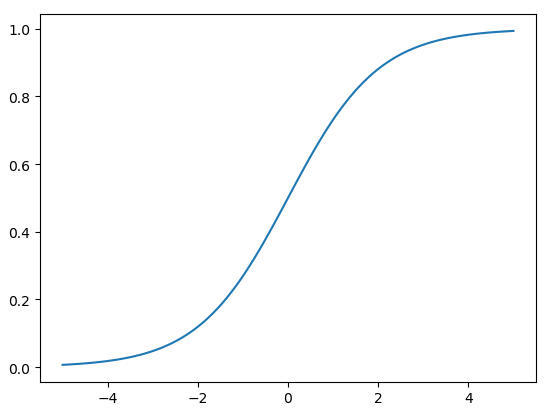
它的导数也非常好计算：

\[f(x) = logistic(x)\\ f(x)' = f(x)[1-f(x)] \]

tanh函数

tanh又称双曲正切。

它的值域是(-1, 1)，所以，它是中心化的

\[tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \]

其函数图像如下所示：

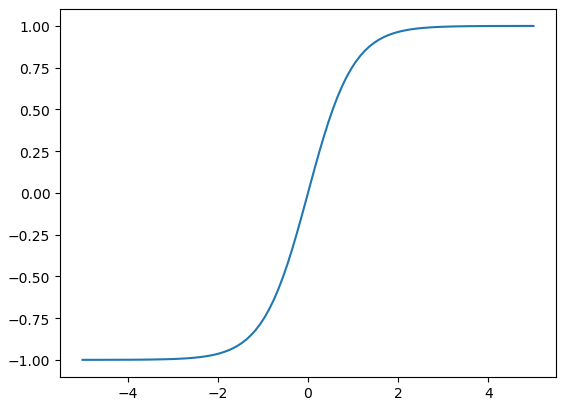
相比之下，tanh比logistic好，第一是中心化，第二是不会导致梯度消失。

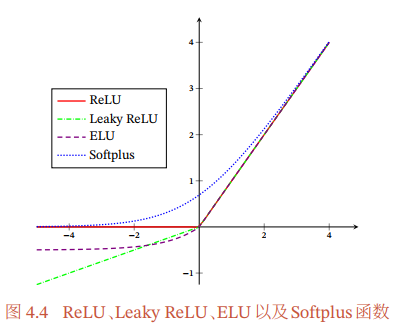
ReLu相关函数

ReLU激活函数

ReLU全称Rectified Linear Unit，修正线性单元。

数学表达式如下：

\[ReLu(x) = max(0, x) \]

函数图像如下：

优势：在x>0时导数为1，一定程度上缓解了梯度消失的问题。

缺点：死亡ReLU问题

死亡ReLU问题

如果某一个隐藏层的ReLU神经元在所有训练数据上都不能被激活（导数都为0），那么在以后的训练中将永远不能被激活

因此，有很多改进的办法。

LeakyReLU函数

LeakyReLU在x<0时也能保持一个很小的梯度\(\gamma\)，其数学表达式为：

\[LeakyReLU(x) = \begin{cases} x, & x>=0\\ \gamma x, & x<0 \end{cases} \]

这里的\(\gamma\)是一个很小的常数。

PReLU函数

PReLU(Parametric ReLU，带参数的ReLU)则是引入一个可学习的参数，其中对于第\(i\)个神经元有：

\[PReLU_i(x) = \begin{cases} x, & x>0\\ \gamma_i x, & x \leq 0 \end{cases} \]

当然也可以设置一组神经元共享一个参数。

ELU函数

ELU全称Exponential Linear Unit，指数线性单元。

它通过调整\(\gamma\)来近似地达到零中心化。

\[ELU(x) = \begin{cases} x, & x>0\\ \gamma(e^x - 1), & x \leq 0 \end{cases} \]

Softplus函数

\[Softplus(x) = \log (1+e^x) \]

接下来在同一张图中对比下这几种激活函数：

Swish函数和GLEU函数

Swish函数

Swish函数是一种自门控激活函数

\[swish(x) = x \sigma(\beta x) \]

\(\beta\)是可学习的或者固定的超参数，\(\sigma\)是一个Logistic函数，起到门控的作用。

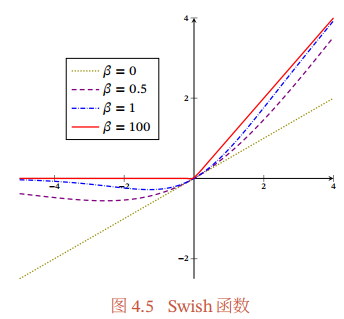
可以看到：

• \(\beta = 0\)，为线性函数
• \(\beta = 100\)，近似为ReLU函数

所以Swish函数可以看成是线性函数和ReLU之间的非线性插值函数。

GELU函数

GELU，全称Gaussian Error Linear Unit，高斯误差线性单元。

\[GELU(x) = xP(X \leq x) \]

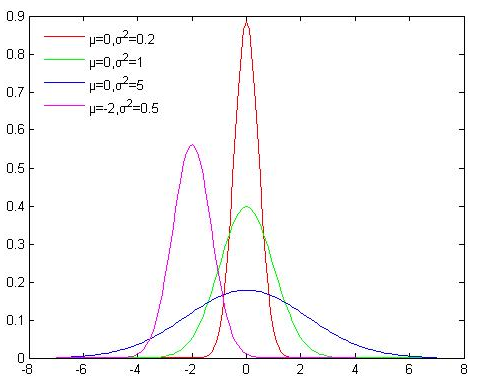
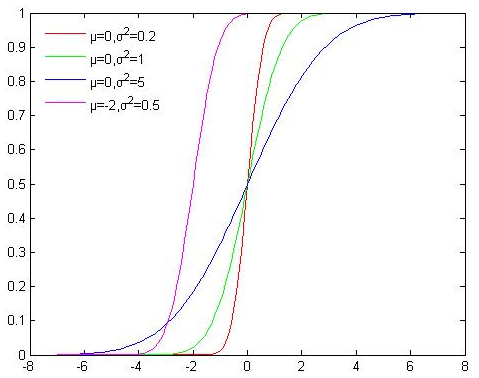
其中\(P(X \leq x)\)是高斯分布\(N(\mu, \sigma^2)\)的累积分布函数。其中\(\mu\)和\(\sigma\)一般为0和1

如下图所示，高斯分布的累积分布函数为S型函数，

高斯分布的概率密度函数为：

高斯分布的累积分布函数为：

因此GELU函数可以用Tanh函数或者Logistic函数来近似。

\[GELU(x) \approx 0.5x(1 + tanh(\sqrt \frac{2}{\pi} (x + 0.044715x^3))) \]

或者

\[GELU(x) \approx x\sigma(1.702x) \]

使用Logistic函数来近似时，GELU相当于一种特殊的Swish函数。

Maxout单元

Maxout的输入是上一层神经元的全部原始输出\(x = [x_1; x_2; ...; x_D]\)

它有\(K\)个权重向量，最后输出最大的那个：

\[z_k = w_k^T x + b_k\\ maxout(x) = \max_{k \in [1, K]}(z_k) \]

其中，\(1 \leq k \leq K\).

---