NOIP2014提高组——飞扬的小鸟

一、题意分析

题目链接

1. 任务：
   • 给出一个长为\(n\)、高为\(m\)的平面，其中有\(k\)组管道（线段）。
   • 小鸟从第\(0\)列任意整数高度位置出发，到达第\(n\)列时，游戏完成。
   • 小鸟每个单位时间沿横坐标方向右移的距离为\(1\)，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度\(X\)，每个单位时间可以点击多次，效果叠加；如果不点击屏幕，小鸟就会下降一定高度\(Y\)。小鸟位于不同列时，\(X\)和\(Y\)可能互不相同。
   • 小鸟高度等于\(0\)或者小鸟碰到管道时，游戏失败 。小鸟高度为\(m\)时，无法再上升。注意：当从位置\(P\)上升\(X\)时，若\(P + X > m\)，则新位置\(P' = m\)。
   • 现在，请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。
2. 数据范围：\(5≤n≤10^4\)，\(5≤m≤10^3\)，\(0≤k\)。

二、算法分析

1. 分析

通过分析，我们发现这是一道完全背包问题。在某个位置，我们有两大类选择：往上飞和往下飞。往上飞又分为多种：往上飞\(1\)下、往上飞\(2\)下······于是，我们来试着定义与描述转移方程。

1). 定义转移方程

\(f(i,j)\)表示从开始到第\(i\)列，第\(j\)个位置所需的最少点击屏幕数。

2). 所求

\(\max_{i=1}^m f(n,i)\)即为所求。

3). 转移方程

设在第\(i\)列飞到第\(i+1\)列的上升高度为\(X[i]\)、下降高度为\(Y[i]\)，第\(i\)列的管道下边沿高度为\(P[i].y1\)、上边沿的高度\(P[i].y2\)；则方程为：

\[f(i,j)= \begin{cases} 0 & i = 0 & and & j \neq 0 \\ INF & j = 0 & or & !P[i].y1 < j < P[i].y2\\ \min_{k=1}^{\lfloor \frac{j-1}{X[i-1]} \rfloor}f(i-1,j-k \times X[i-1])) & i \neq 0 & and & j \neq 0 & and & j + Y[i - 1] > m\\ \min(f(i-1,j+Y[i - 1]),\min_{k=1}^{\lfloor \frac{j-1}{X[i-1]} \rfloor}f(i-1,j-k \times X[i-1])) & i \neq 0 & and & j \neq 0 & and & j + Y[i - 1] \leq m\\ \min(f(i-1,j),\min_{k=1}^{m-1}(f(i-1,j)+\lfloor\frac{m-1-j}{X[i-1]}\rfloor))+1 & i \neq 0 & and & j=m \end{cases} \]

2. 优化

我们发现，这样做时间复杂度为\(O(m^2n)\)，肯定超时。

若当前点击屏幕，小鸟的上升高度为\(2\)；那么依据方程且只考虑上升的情况，有：

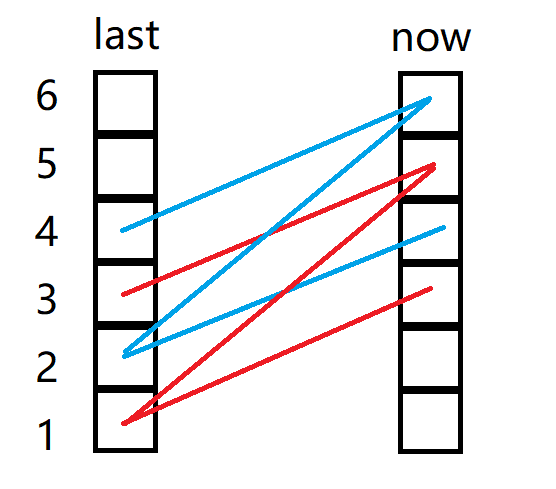
不难发现，这里还有子问题重叠。若只考虑上升，我们发现：当前第\(3\)个格子汇总了从前面格子向上飞\(1\)下的最少点击屏幕数，第\(5\)个格子汇总了从前面格子向上飞\(2\)下的最少点击屏幕数。因此，若只考虑上升，当前第\(i\)个格子应汇总了从前面格子向上飞\(\lfloor \frac{i}{X[i-1]} \rfloor\)下的最少点击屏幕数。

因此，我们求当前第\(i\)个格子应汇总的上升情况，就是求当前第\(i-X[i-1]\)个格子的上升情况再\(+1\)（因为又“远了”一个上升高度），与上次求好的第\(i-X[i-1]\)个格子再\(+1\)求最小值。我们令\(rec(i,j)\)表示第\(i\)列第\(j\)个位置，若只考虑上升的最少点击屏幕数；那么有：

\[rec(i,j)= \begin{cases} INF & j = 0 & or & j-X[i-1] \leq 0 \\ \min(rec(i-1,j-X[i-1]),f(i-1,j-X[i-1])) + 1 & j \neq 0 & and & j-X[i-1] >0 \end{cases} \]

再结合下降的情况，我们就可以用\(O(mn)\)的时间复杂度解决此题了。

三、完整代码

#include <cstdio>
#include <cstring>

const int N = 11000;
const int M = 1100;
const int INF1 = 0x3f3f3f3f;
struct node{
	int x, y1, y2;
};
node a[N];
struct node1{
	int v1, v2;
};
node1 v[N];
int f[N][M], rec[M];
int n, m, p, x, y1, y2;

inline int min1(int x, int y){
	return x < y ? x : y;
}

int main(){
	scanf("%d%d%d", &n, &m, &p);
	for (int i = 0; i < n; ++i) scanf("%d%d", &v[i].v1, &v[i].v2);
	
	for (int i = 1; i <= n; ++i) a[i].y1 = 0, a[i].y2 = m + 1;
	for (int i = 1; i <= p; ++i) { 
		scanf("%d%d%d", &x, &y1, &y2);
		a[x].y1 = y1;
		a[x].y2 = y2;
	} 
	a[0].x = 0;
	for (int i = 1; i <= n; ++i) { 
		a[i].x = a[i - 1].x;
		if (a[i].y1 != 0 || a[i].y2 != m + 1) ++a[i].x;
	} 
	
	memset(f, 0x3f, sizeof f);
	for (int i = 1; i <= m; ++i) f[0][i] = 0;
	
	for (int i = 1; i <= n; ++i) { 
		memset(rec, 0x3f, sizeof rec);
		for (int j = v[i - 1].v1; j <= a[i].y1; ++j) rec[j] = min1(f[i - 1][j - v[i - 1].v1], rec[j - v[i - 1].v1]) + 1;
		
		for (int j = a[i].y1 + 1; j < a[i].y2; ++j) { 
			if (j - v[i - 1].v1 > 0) f[i][j] = rec[j] = min1(f[i][j], min1(f[i - 1][j - v[i - 1].v1], rec[j - v[i - 1].v1]) + 1);
			if (j + v[i - 1].v2 <= m) f[i][j] = min1(f[i][j],f[i - 1][j + v[i - 1].v2]);
		} 
		
		if (a[i].y2 == m + 1 && v[i - 1].v1 != 0) { 
			for (int j = 1; j < m; ++j) f[i][m] = min1(f[i][m], f[i - 1][j] + (m - 1 - j) / v[i - 1].v1 + 1);
			f[i][m] = min1(f[i][m], f[i - 1][m] + 1);
		} 
		
		int cnt = 0;
		for (int j = 1; j <= m; ++j) if (f[i][j] == INF1) ++cnt;
		
		if (cnt == m) { 
			printf("0\n%d\n", a[i].x - 1);
			return 0;
		} 
	} 
	
	int ans = INF1;
	for (int i = 1; i <= m; ++i) ans = min1(ans, f[n][i]);
	
	printf("1\n%d\n", ans);
	
	return 0;
}