【学习笔记】四边形不等式优化
四边形不等式优化
日期:2020-08-23
一、引入
在区间类动态规划(\(2D1D\))中,有一类常见的、复杂度为\(O(n^3)\)的转移方程:
其中,\(f(i,j)\)表示\([i,j]\)这个区间的某个最优值;\(w(i,j)\)表示转移\((i,j)\)时的代价。
显然地,如果问题中的\(n\)在\(100\)以内(如:[NOI1995]石子合并),我们可以很顺利地解决;\(n\)如果超过\(1000\),我们就需要一个更好的方法了。如果\(w(i,j)\)满足一些特殊的性质,我们就可以进行优化。
二、定义
1. 区间包含单调性
如果对于任意\(l \leq l' \leq r' \leq r\) ,均有\(w(l',r')\leq w(l,r)\)成立,则称函数\(w\)对于区间包含关系具有单调性。
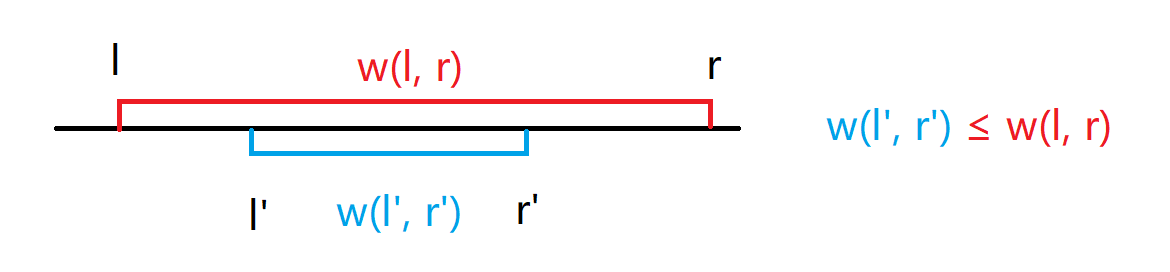
如上图,该定义可以理解为:被包含的小区间的\(w\)不大于大区间的\(w\)。
2. 四边形不等式
如果对于任意\(l_1 \leq l_2 \leq r_1 \leq r_2\),均有\(w(l_1, r_1) + w(l_2,r_2) \leq w(l_1, r_r) + w(l_2, r_1)\)成立,则称函数\(w\)满足四边形不等式(简记为“交叉小于包含”)。
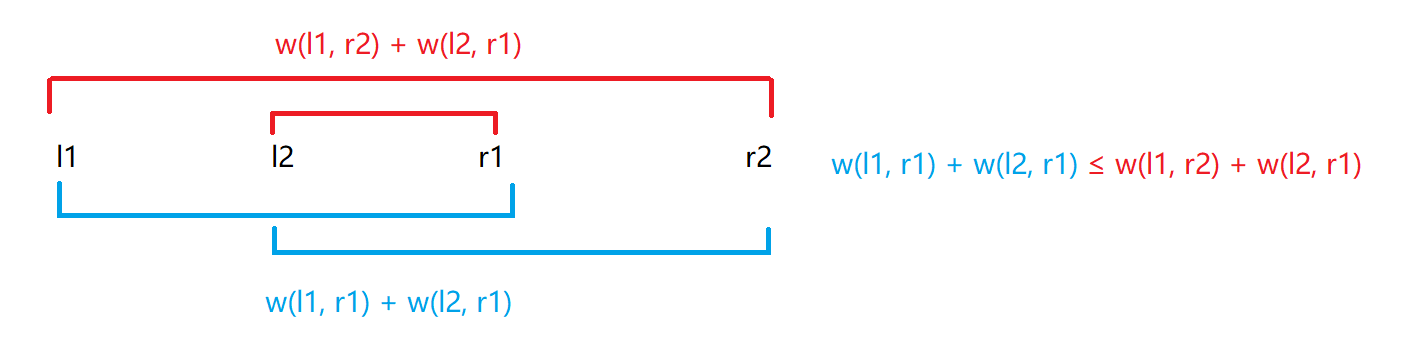
如上图,该定义可以理解为:两个交叉区间\(w\)的和不大于大区间和小区间\(w\)的和。
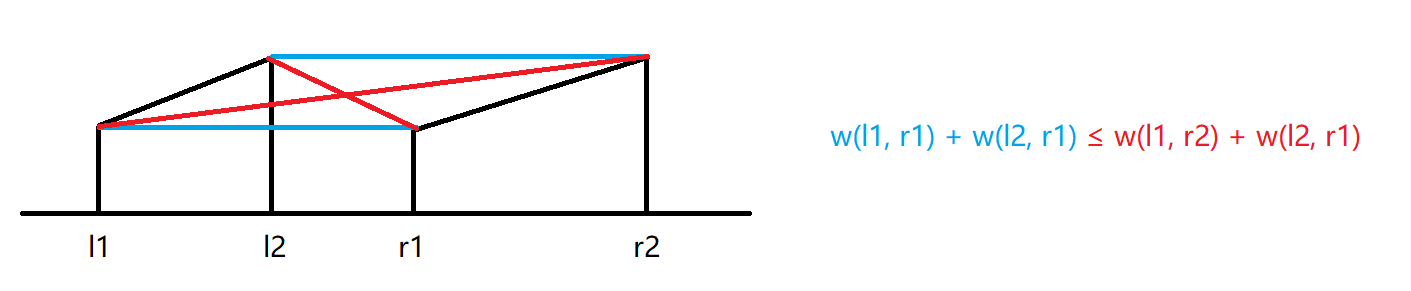
同时,该不等式可以形象化为上图(红线长度和大于等于蓝线长度和)。
三、定理及证明
定理\(1\)
若满足关于区间包含的单调性的函数\(w(l,r)\)满足四边形不等式,则状态\(f(l,r)\)也满足四边形不等式。
证明
定义\(g(l,r,k)=f(l,k)+f(k+1, r)+w(l,r)\)表示当决策为\(k\)时的状态值,任取\(l_1 \leq l_2 \leq r_1 \leq r_2\)。记\(u= \min_{k=l_1}^{l_2-1}g(l_1,r_2,k)\),\(v=\min_{k=l_2}^{r_1-1}g(l_2,r_1,k)\),分别表示状态\(f(l_1,r_2)\)和\(f(l_2,r_1)\)的最优决策点。
试用数学归纳法证明\(f(l_1,r_1)+f(l_2, r_2) \leq f(l_1,r_2)+f(l_2,r_1)\)成立。
归纳假设过程如下:
若\(u \leq v\),则\(l_1 \leq u < r_1\),\(l_2 \leq v < r_2\)
当\(i=1\),\(j=2\)时,
因为\(f(1,1)=f(2,2)=f(3,3)=0\);\(f(1,2)=w(1,2)\),\(f(2,3)=w(2,3)\);\(f(1,3)\geq w(1,3)\)
由四边形不等式可知,
\(w(1,2)+w(2,3) \leq w(1,3)+w(2,2)\)
显然,\(f(1,2)+f(1,3) \leq f(1,3)+f(2,2)\)成立。
我们假设\(f(u+1,r_1)+f(v+1,r_2)\leq f(u+1,r_2)+f(v+1,r_1)\)成立,
对于\(l_1 \leq l_2 \leq r_1 \leq r_2\),显然有,
\(f(l_1, r_1) \leq f(l_1,u)+f(u+1,r_1)+w(l_1,r_1)\)
\(f(l_2,r_2)\leq f(l_2,v)+f(v+1,r_2)+w(l_2,r_2)\)
\(f(l_1,r_1) + f(l_r,r_2) \leq f(l_1,u) + f(u+1,r_1) + w(l_1,r_1) + f(l_2,v)+f(v+1,r_2)+w(l_2,r_2)\)
又因为函数\(w\)满足四边形不等式,
\(w(l_1,r_1)+w(l_2,r_2) \leq w(l_1,r_2)+w(l_2,r_1)\),所以
$ f(l_1,u) + f(u+1,r_1) + w(l_1,r_1) + f(l_2,v)+f(v+1,r_2)+w(l_2,r_2) \leq$
$f(l_1,u) + f(u+1,r_1) + w(l_1,r_2) + f(l_2,v)+f(v+1,r_2)+w(l_2,r_1) $
又因为\(f(u+1,r_1)+f(v+1,r_2)\leq f(u+1,r_2)+f(v+1,r_1)\)成立,所以
$ f(l_1,u) + f(u+1,r_1) + w(l_1,r_1) + f(l_2,v)+f(v+1,r_2)+w(l_2,r_2) \leq$
\(f(l_1,u) + f(u+1,r_2) + w(l_1,r_2) + f(l_2,v)+f(v+1,r_1)+w(l_2,r_1) =\)
\(f(l_1,r_2)+f(l_2,r_1)\)
即\(f(l_1,r_1)+f(l_2, r_2) \leq f(l_1,r_2)+f(l_2,r_1)\)成立
同理,可证\(v < u\)时\(f(l_1,r_1)+f(l_2, r_2) \leq f(l_1,r_2)+f(l_2,r_1)\)成立
综上,\(f(l_1,r_1)+f(l_2, r_2) \leq f(l_1,r_2)+f(l_2,r_1)\)成立
定理\(2\)
若状态\(f(l,r)\)满足四边形不等式,记\(s(l,r)=\min\{k:f(l,k)+f(k+1,r)\}\)表示最优决策点,则\(s\)单调,即\(s(l,r-1) \leq s(l, r) \leq s(l+1,r)\)。
证明
记\(u = s(l,r)\),\(k_1=s(l,r-1)\),\(k_2=s(l+1,r)\),有如下证明:
若\(k1 > u\),则\(u + 1 \leq k_1 + 1 \leq r-1\leq r\)。
因此,根据四边形不等式有
\(f(u+1,r-1)+f(k_1+1, r) \leq f(u+1,r)+f(k_1+1,r-1)\)
再根据\(u\)是状态\(f(l,r)\)的最优决策点可知
\(f(l,u)+f(u+1,r) \leq f(l,k_1)+f(k_1+1,r)\)
将以上两个不等式相加,得
\(f(l,u)+f(u+1,r-1) \leq f(l,k_1)+f(k_1+1,r-1)\)
即\(g(l,r-1,u) \leq g(l,r-1,k_1)\),但这与\(k1\)是最小的最优决策点矛盾,因此\(k_1 \leq u\)。
同理,可证\(u \leq k_2\)。
综上,\(k_1 \leq u \leq k_2\),即\(s(l,r-1) \leq s(l, r) \leq s(l+1,r)\)。
四、例题
1. 题意
\(N\)(\(1 \leq N \leq 100\))堆石子排成一排,规定每次只能选相邻的两堆石子合并成一堆,得分为新的一堆的石子数,求将它们合并成\(1\)堆的最小得分和最大得分。
2. 算法分析
我们先可以得到一个时间复杂度为\(O(n^3)\)的方程(最小得分):
我们发现,该方程符合区间\(DP\)中的\(2D1D\)(两维·一维),用上述方法,验证其单调性和符合四边形函数。我们发现,它符合该特征。于是,该方程可以化简为(用\(p\)记录最优决策点):
注意:最大得分不符合该特征,所以不能采用该优化。
3. 完整代码
#include <bits/stdc++.h>
const int N = 220;
int n, a[N], s[N], f[N][N], p[N][N];
inline int solve(int opt){
if (~opt) memset(f, 0x3f, sizeof f);
else memset(f, 0, sizeof f);
for (int i = 1; i < n << 1; ++i) f[i][i] = 0, p[i][i] = i;
for (int l = 2; l <= n; ++l)
for (int i = 1; i <= (n << 1) - l; ++i) {
int j = i + l - 1;
for (int k = ~opt ? p[i][j - 1] : i; k <= (~opt ? p[i + 1][j] : j - 1); ++k) {
int val = f[i][k] + f[k + 1][j];
if (val * opt < f[i][j] * opt) {
f[i][j] = val;
p[i][j] = k;
}
}
f[i][j] += s[j] - s[i - 1];
}
int res = 0;
if (~opt) res = 0x3f3f3f3f;
for (int i = 1; i <= n; ++i)
res = res * opt < f[i][i + n - 1] * opt ? res : f[i][i + n - 1];
return res;
}
int main(){
freopen("main.in", "r", stdin);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", a + i);
a[i + n] = a[i];
}
s[0] = 0;
for (int i = 1; i < n << 1; ++i) s[i] = a[i] + s[i - 1];
printf("%d\n%d\n", solve(1), solve(-1));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号