CSP-J 2020题解
CSP-J 2020题解
日期:2020-12-13
前言:闲来无事,蒟蒻要来做做历届\(CSP-J \ / \ NOIP\)的题了,毕竟明年比赛时就初三了qwq。
A. 优秀的拆分
核心算法:模拟。
水题,直接上代码:
#include <bits/stdc++.h>
using namespace std;
int n, k = 1 << 30;
int main(){
scanf("%d", &n);
if (n & 1) printf("-1\n");
else {
while (k) {
if (n & k) printf("%d ", k);
k >>= 1;
}
}
return 0;
}
B. 直播获奖
水题,因为选手成绩不超过\(600\),所以开个桶计数,每次扫一遍即可。
核心算法:计数排序。
时间复杂度:\(O(wn)\),其中\(w\)是常数且等于\(600\)。
\(Hint\):做题时注意数据范围!
#include <bits/stdc++.h>
using namespace std;
const int M = 660;
int cnt[M];
int n, w, x;
int main(){
scanf("%d%d", &n, &w);
memset(cnt, 0, sizeof cnt);
for (int i = 1; i <= n; ++i) {
scanf("%d", &x);
++cnt[x];
int p = i * w / 100;
if (!p) p = 1;
for (int j = 600; j >= 0; --j)
if (cnt[j]) {
p -= cnt[j];
if (p <= 0) {
printf("%d ", j);
break;
}
}
}
return 0;
}
C. 表达式
1. 分析
这是最难的一道题目,首先可以考虑建一棵表达式树,样例\(2\)如下图所示:
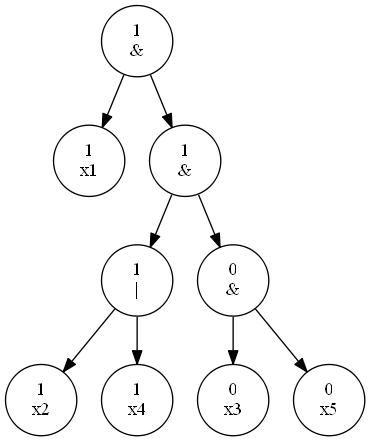
我们尝试预处理每个\(x\)更改后最后结果的值,所以自顶向下搜索。由于\(\&\)和\(|\)是短路运算符,所以:
- 当运算符为\(\&\)时,若一侧为\(0\),则另一侧无论怎么修改,也无法改变最后结果;
- 当运算符为\(|\)时,若一侧为\(1\),则另一侧无论怎么修改,也无法改变最后结果。
根据这个性质,在搜索时,若一侧出现上述情况,则将另一侧的所有\(x\)打上\(false\)标记,表示对结果无影响。
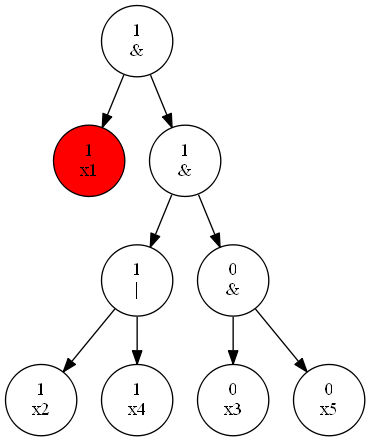
令未更改时最后结果为\(ans\)。若\(x_i\)有\(false\)标记,结果就是\(ans\);否则结果为\(!ans\)。
2. 小结
核心算法:树形结构,短路运算符。
时间复杂度:\(O(n+q)\)。
\(Hint\):遇到表达式时,可以考虑建表达式树;注意分析短路运算符的性质。
#include <bits/stdc++.h>
const int L = 1.1e6;
const int N = 1.1e5;
bool a[N], flag[N];
char s[L];
int l, n, top = 1, num = 0, q;
int sta[N];
struct node{
int val, opt, l, r;
void init(int x, int z, int ll, int rr){
val = x; opt = z;
l = ll; r = rr;
}
};
node tree[L];
void dfs(int p, bool mark){
if (!tree[p].l && !tree[p].r) {
flag[tree[p].opt] = mark;
return ;
}
if (!mark) {
dfs(tree[p].l, mark);
dfs(tree[p].r, mark);
return ;
}
dfs(tree[p].l, tree[tree[p].r].val ^ tree[p].opt);
dfs(tree[p].r, tree[tree[p].l].val ^ tree[p].opt);
}
int main(){
gets(s + 1);
l = strlen(s + 1);
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", a + i);
for (int i = 1; i <= l; ++i) {
if (s[i] == 'x') {
int id = 0;
for (int j = i + 1; j <= l; ++j) {
if (std::isdigit(s[j])) id = id * 10 + (s[j] - 48);
else { i = j; break; }
}
sta[top++] = ++num;
tree[num].init(a[id], id, 0, 0);
}
if (s[i] == '&') {
int y = sta[--top], x = sta[--top];
sta[top++] = ++num;
tree[num].init(tree[x].val & tree[y].val, 0, x, y);
}
if (s[i] == '|') {
int y = sta[--top], x = sta[--top];
sta[top++] = ++num;
tree[num].init(tree[x].val | tree[y].val, 1, x, y);
}
if (s[i] == '!') tree[sta[top - 1]].val ^= 1;
}
bool ans = tree[sta[1]].val;
dfs(sta[1], true);
scanf("%d", &q);
for (int x, i = 1; i <= q; ++i) {
scanf("%d", &x);
printf("%d\n", ans ^ flag[x]);
}
return 0;
}
D. 方格取数
手推样例后不难发现,不同路线的某一部分可能重叠,由此可以想到动态规划。
1. 分析1
初始地,我们定义最简单的转移方程。令\(f(i, j)\)表示从\((1,1)\)走到\((i,j)\)位置,取到数的和的最大值。
我们按列转移,则有转移方程:
\(\sum\)可用前缀和优化,令\(S[k]\)表示\(\sum_{t=1}^k a[j][t]\),则原方程可优化为:
至此,我们得到了一个\(O(n^2m)\)的\(70pts\)算法。
2. 分析2
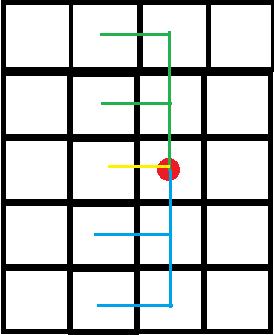
画图可知,一个点只能由它的上和下转移得来(左包含在内);否则就是非法的。
于是,我们定义方程\(f(i,j,0/1)\)表示从\((1,1)\)走到\((i,j)\)位置,由上/下转移过来,取到数的和的最大值。
同样按列转移,则有方程:
注意:两个方程循环顺序不同,还需理清边界条件。
时间复杂度:\(O(nm)\)。可得满分。
3. 小结
核心算法:动态规划。
\(Hint\):先推出最简单的方程,再画图/分析,考虑优化。
#include <bits/stdc++.h>
using std::max;
const int N = 1100;
int n, m, map[N][N];
long long f[N][N][2];
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) scanf("%d", &map[i][j]);
for (int i = 1; i <= m; ++i) f[0][i][0] = f[n + 1][i][1] = -1e10;
for (int i = 1; i <= n; ++i) f[i][0][0] = f[i][0][1] = -1e10;
f[0][1][0] = 0;
for (int j = 1; j <= m; ++j) {
for (int i = 1; i <= n; ++i) f[i][j][0] = max(f[i - 1][j][0], max(f[i][j - 1][0], f[i][j - 1][1])) + map[i][j];
for (int i = n; i >= 1; --i) f[i][j][1] = max(f[i + 1][j][1], max(f[i][j - 1][0], f[i][j - 1][1])) + map[i][j];
}
printf("%lld\n", f[n][m][0]);
return 0;
}

