【模板】线段树

日期：2020-05-31

【模板】线段树

一、【模板】问题

题目链接（洛谷P3372）

1. 题意分析

给定一个数列，现有两种操作：

将区间$[x,y]$内每个数加上$k$；
输出区间$[x,y]$内每个数的和。

2. 暴力分析

修改：暴力对区间内每个数加上$k$，时间复杂度：$O(n)$；
查询：暴力求区间内每个数的和，时间复杂度：$O(n)$。

操作次数为$m$，则总时间复杂度为$O(nm)$。

$\because 1 \le n, m \le 10^5$，

$\therefore O(nm)=O(10^{10})$，故$TLE$。

所以，我们需要一种更好的方法（数据结构）。

二、线段树概念

1. 概念

线段树，一种形如二叉树的数据结构，适用于处理区间操作。线段树的每个结点存储一个区间，如下图所示：

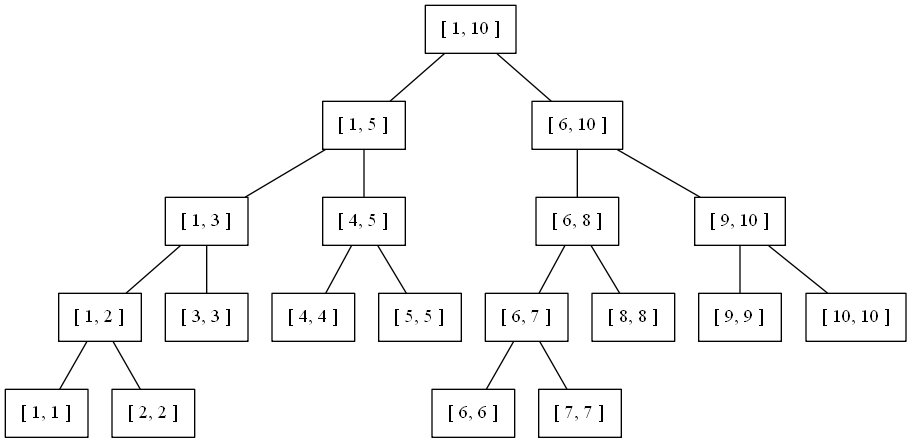
2. 问题实现

1). 建树

输入 #1

对于此题，可以使每个结点存储其管辖区间内每个数的和。以输入样例为例：

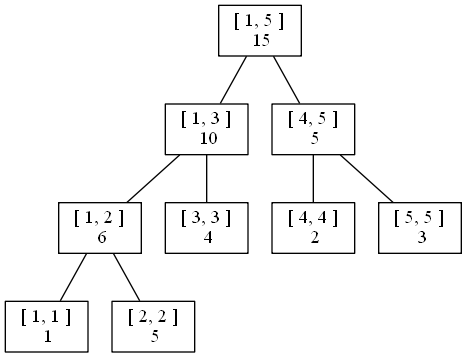
2). 修改

无论是在修改还是在查找时，首先应锁定修改/查询区间所包含的线段（具体实现见代码）

假设我们要将$[1,3]$区间内的数都加上$2$，我们应该如何修改呢？

我们绝对不能把$2$加到每一个区间上（即$[1,1],[2,2],[3,3]$），否则就会比暴力还要慢。

我们可以利用懒标记（敲黑板~）来只修改管辖$[1,3]$区间的这条线段，如下图所示：

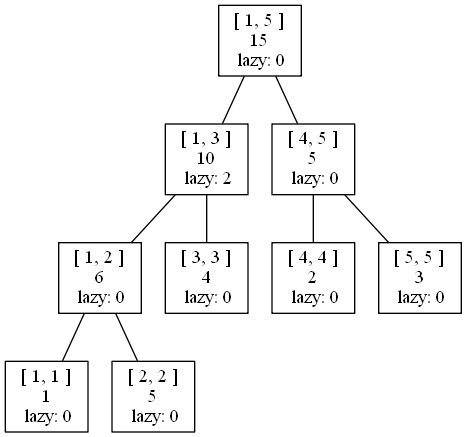
修改完毕后，需要进行回溯操作（$push \ up $）。要将正确结果（包含子树的修改）返回本身的和，直至树根为止。若令管辖任意区间的这条线段的和为$sum$（$sum$不含懒标记），我们可以得出$[x,y]$（非叶结点）区间的$sum$。

其左子树的答案为：$lans = [x, \frac{x + y}{2}].sum + [x, \frac{x + y}{2}].lazy \times (\frac{x + y}{2} - x + 1)$，即左子树的$sum$与其懒标记乘上元素个数的和。

其右子树的答案为：$rans = [\frac{x + y}{2} + 1, y].sum + [\frac{x + y}{2}+1, y].lazy \times (y-\frac{x + y}{2})$，即右子树的$sum$与其懒标记乘上元素个数的和。

故$[x,y]$的$sum$为：$[x,y].sum = lans + rans$，即其左子树的答案与右子树答案的和。

回溯后如图所示：

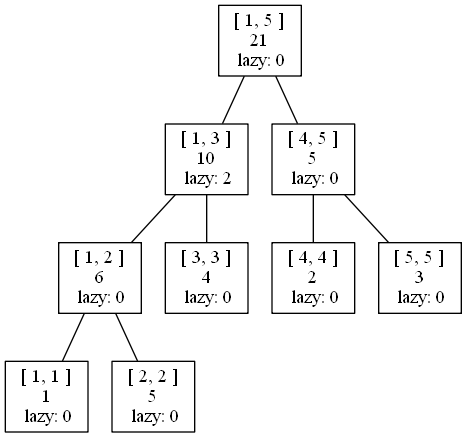
假设我们又要将$[3,5]$区间内的数都加上$3$。

那么，因为$[3,5]$的一部分在$[1,3]$范围内，所以这时管辖$[1,3]$区间这条线段的懒标记只有部分还正确，即$[1,2]$区间内的每个数要加$2$，而$[3,3]$区间内的每个数要加$5$（$2+3$）。所以，我们需要将懒标记下放~~（因为懒，所以记不住那么多信息qwq）~~，即$push \ down$操作：

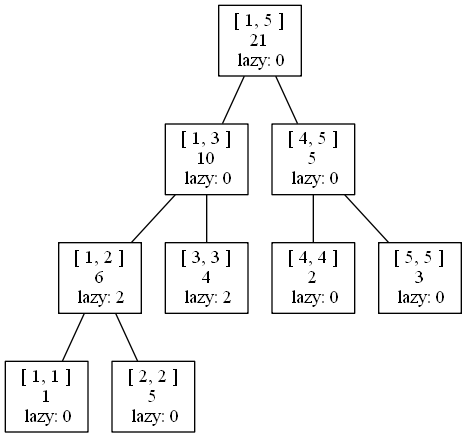
然后，再进行分割线以上的操作，即修改管辖$[3,3]$区间和$[4,5]$区间的这两条线段的懒标记，如下图所示：

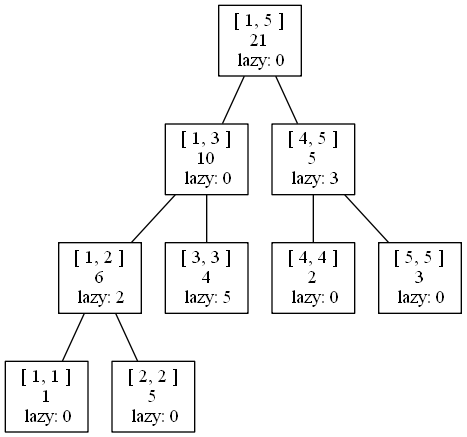
回溯：

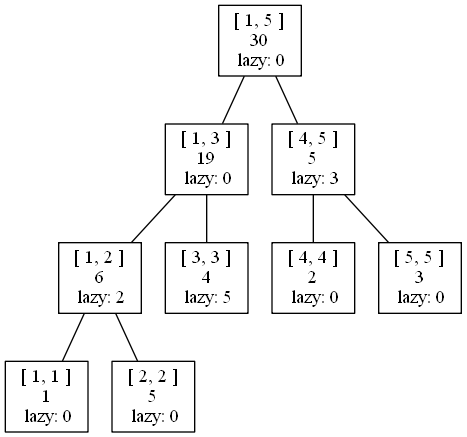
3). 查询

查询操作和修改操作类似，假设我们要查找$[1,2]$区间内每个数的和，其实就是$[1,2].sum+[1,2].f \times 2$。

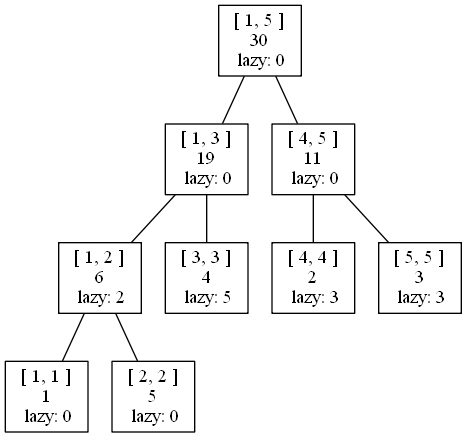
假设我们要查找$[1,4]$区间内每个数的和，即查询管辖$[1,3]$区间和$[4,4]$区间的两条线段的答案，$[1,3]$的答案是$19$（显而易见），而求$[4,4]$的答案时，需要先下放$[4,5]$的懒标记：

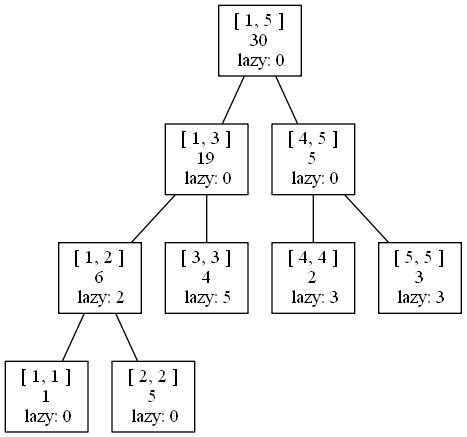
求出$[4,4]$答案，即$5$。于是最终的答案就是$19 + 5 = 24$。

不要忘记回溯，以方便下次操作：

三、线段树的构建与操作

0. 定义结点

首先，我们要定义线段树的结点（链表实现）。对于此题而言，我们做出如下定义：

struct node{ 
    int a, b; //表示该结点的管辖区间[a, b]
    int *l, *r; //分别表示该结点的左右子树
    long long s, f; //s表示[a,b]区间每个数的和，f表示懒标记
    node(int x, int y, long long ss){ //构造函数
        a = x; b = y; //x、y分别给a、b赋值
        l = r = NULL; //初始化指针
        s = ss; //ss为叶结点赋值
        f = 0; //初始化懒标记
    } 
};
node *root; //根结点

1. 建树

定义结点后，我们需要建起一棵线段树。我们一般递归建树。

void build(node *&root, int x, int y){ 
	root = new node(x, y, a[x]); //创建新的结点
	if (x < y){ //有左右子树（非叶结点）
		int mid = x + y >> 1; //找[x, y]中点
		build(root->l, x, mid); //建左子树
		build(root->r, mid+1, y); //建右子树
		root->s = root->l->s + root->r->s; //回溯：[x,y]区间内每个数的和
	}
}

built(root, 1, n); //建树

2. 懒标记下放和回溯

void push_down(node *p){ //下放懒标记
	p->l->f += p->f; //下放给左子树
	p->r->f += p->f; //下放给右子树
	p->f = 0;
}
void push_up(node *p){ //回溯
	long long s1 = 1ll * p->l->f * (p->l->b - p->l->a + 1) + p->l->s; //计算左子树答案
	long long s2 = 1ll * p->r->f * (p->r->b - p->r->a + 1) + p->r->s; //计算右子树答案
	
	p->s = s1 + s2; //计算自己（p）的和
}

3. 修改

void add(node *p, int a, int b, int c){ 
	if(a <= p->a && p->b <= b){ //查询范围完全覆盖线段范围
		p->f += c; //该线段的懒标记加上c
		return ; //注意返回
	}
	
	if (p->f != 0) push_down(p); //懒标记下放
	
	int mid = p->a + p->b >> 1; //求p[a, b]的中点
	if (a <= mid) add(p->l, a, b, c); //判断是否在左子树范围内
	if (mid < b) add(p->r, a, b, c); //判断是否在右子树范围内
	
	push_up(p); //回溯
}

4. 查询

long long check(node *p, int a, int b){ 
	if (a <= p->a && p->b <= b) return 1ll*p->f * (p->b - p->a + 1) + p->s;//返回p所对应的答案
	
	if (p->f != 0) push_down(p); //懒标记下放
	
	int mid = p->a + p->b >> 1; //求p[a, b]的中点
	long long s1 = 0, s2 = 0;
	if (a <= mid) s1 = check(p->l, a, b); //求在左子树范围内的答案
	if (mid < b) s2 = check(p->r, a, b); //求在右子树范围内的答案
	
	push_up(p); //回溯
	
	return s1 + s2; //返回答案
}

四、完整代码

#include <cstdio>
const int N = 110000;
struct node{ 
	int a, b;
	node *l, *r;
	long long s, f;
	node(int aa, int bb, long long ss){ 
		a = aa; b = bb;
		l = r = NULL;
		s = ss;
		f = 0;
	}
};
node *root;
long long a[N];
int n, m;

void build(node *&root, int x, int y){ 
	root = new node(x, y, a[x]);
	if (x < y){ 
		int mid = x + y >> 1;
		build(root->l, x, mid);
		build(root->r, mid+1, y);
		root->s = root->l->s + root->r->s;
	} 
} 
void push_down(node *p){ 
	p->l->f += p->f;
	p->r->f += p->f; 
	p->f = 0;
} 
void push_up(node *p){ 
	long long s1 = p->l->f * (p->l->b - p->l->a + 1) + p->l->s;
	long long s2 = p->r->f * (p->r->b - p->r->a + 1) + p->r->s;
	
	p->s = s1 + s2;
} 
void add(node *p, int a, int b, long long c){ 
	if(a <= p->a && p->b <= b){ 
		p->f += c;
		return ;
	} 
	
	if (p->f != 0) push_down(p);
	
	int mid = p->a + p->b >> 1;
	if (a <= mid) add(p->l, a, b, c);
	if (mid < b) add(p->r, a, b, c);
	
	push_up(p);
}
long long check(node *p, int a, int b){ 
	if (a <= p->a && p->b <= b) return p->f * (p->b - p->a + 1) + p->s;
	
	if (p->f != 0) push_down(p);
	
	int mid = p->a + p->b >> 1;
	long long s1 = 0, s2 = 0;
	if (a <= mid) s1 = check(p->l, a, b);
	if (mid < b) s2 = check(p->r, a, b);
	
	push_up(p);
	
	return s1 + s2;
} 

int main(){ 
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; ++i) scanf("%lld", a + i);
	
	build(root, 1, n);
	
	for (int i = 1; i <= m; ++i){
		int d, x, y;
		long long c;
		
		scanf("%d", &d);
		
		if (d == 1){ 
			scanf("%d%d%lld", &x, &y, &c);
			add(root, x, y, c);
		} 
		if (d == 2){ 
			scanf("%d%d", &x, &y);
			long long ans = check(root, x, y);
			printf("%lld\n", ans);
		} 
	}
	
	return 0;
}

posted @ 2020-06-06 21:40 _lhy 阅读(147) 评论(2) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Young06

路漫漫其修远兮，吾将上下而求索。

【模板】线段树

【模板】线段树

一、【模板】问题

1. 题意分析

2. 暴力分析

二、线段树概念

1. 概念

2. 问题实现

1). 建树

2). 修改

3). 查询

三、线段树的构建与操作

0. 定义结点

1. 建树

2. 懒标记下放和回溯

3. 修改

4. 查询

四、完整代码

公告