= 参考/转自：
1 ---https://blog.csdn.net/u010720661/article/details/63253509
2----http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
3----徐亦达 机器学习课程（优酷）
4 -----https://blog.csdn.net/u010480899/article/details/55656209
不知道为什么，之前学习卡尔曼滤波器，总感觉差了点什么，很多人只知道是5个公式用一用就好，对于我则是不理解毋宁不用。
直到参考上面的才从感性上理解，之前都是理性（公式）。也可能是之前的积累吧。这里没有我自己的东西（如果整理算的话，那算一点），都是上面参考的。
卡尔曼滤波最好的作用是在。。。。。 这里一些介绍就不写了，参考链接很全，下面的思路讲解和图片部分来自于参考链接。
如果表述不对的地方烦请大家批评指正，避免我误人子弟。
（这里是通过数据融和方式解释卡尔曼滤波，还有一种是通过估计的均方误差阵达到最小时，求得其滤波增益K的方式，所以，卡尔曼滤波也被称为最优的。。。。。）
下面直接给出线性kalman filter 的5个公式：
然后，一个一个公式去搞定和推倒。现在谈论一个场景----直线运动：
假设，一个人开着一辆车在一条比值的道路上行驶，我们的目的是要知道这个人的状态信息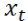
（包含车的位置和速度信息
），并假设车的
加速度为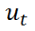
。
然后，根据参考链接4的表述：
然后，卡尔曼滤波的第一个公式我们知道了。这个式子的意义是：我们通过车辆“理论上”的速度、加速度、初始位置，使用刚体运动知识估计出刚体运动的状态。
但是，通常我们在项目中可以知道，这种估计因为传感器、现实生活都是非“理想的、理论上的”，所以，这种估计是比较简陋粗略、比较不准确的。这时候就要提升精度。
第一个公式也就是正常的初中物理中介绍的，没问题吧。
-------------------------------------------------------------------------
如何提高估计准确性？
假设，世界上有上帝/神，上帝/神 可以知晓万物的一切，当神看到我们人类在计算一辆车的直线运动状态的时候，他心里肯定是这样想的：”傻瓜“的人类，车载运行中有很多
的不确定，你考虑到了吗？！！！！然后，神就把这些信息传递给我们人类，人类就分析：哪里有不确定呀？？？？？，然后我们就思考了，
假设在0时刻：
1、我们不确定车子是完全从坐标原点O出发的？
2、同时，我们也不确定0时刻车子的速度一定为v，
3 、也不确定如果速度不为v，这种情况对车子的位置影响有多少？
4、也不确定如果车辆初始触发位置不为原点O，是否对速度有影响？
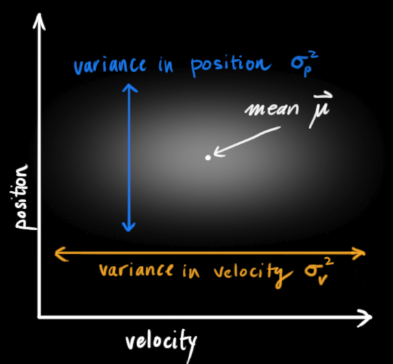
看到上面的四个疑问是不是会联想到，这是位置和速度他们自己和自己的关系，还有就是互相的关系，然后答案就是协方差，在多维中就是协方差矩阵!!!!!
下面是参考链接4中介绍的：
这就是卡尔曼滤波公式的第二个公式，考虑了不确定性的传递和传递本身的不确定性。。。
下面是参考链接
第二个公式也就是对估计中不确定性给显示表达出来，没问题吧。
-------------------------------------------------------------------------
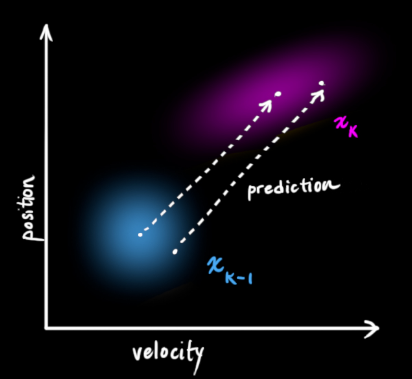
很明显，目前这两个公式都是依据我们前一个（t-1），理论推算到t的，对吧，所以这两个公式归纳在predict环节
---------------------------------------------------------------------------------------------------------------------------------------------------------------
接下来，我们得到后面3个公式，后面的公式涉及到传感器问题，现在，我们通过卡尔曼公式1 、 2 ，得到了目标的位置预测，实际上
我们还有一些传感器对目标进行测量，比如说车上的里程计。这时候后面的3个公式的讲解将参考‘参考链接1’和‘参考链接4’的穿插结合。
在t时刻，假设车子出发时，车里程表的数值为0，也就是车子在运动中其车里程表的读数就是车子直线运动的位置信息。或者在初始时刻
记录车子的gps，在t时刻再记录gps，然后两个gps之间的距离就是车子位置状态测量的距离（这种在《多源信息融和》书中讲的是”量测“信息）
不管其他，总之，就是车辆在真实位置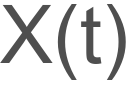
中，这个位置是要估计的，当然我们不知道，然后传感器就”看到“车在这个位置，并输出
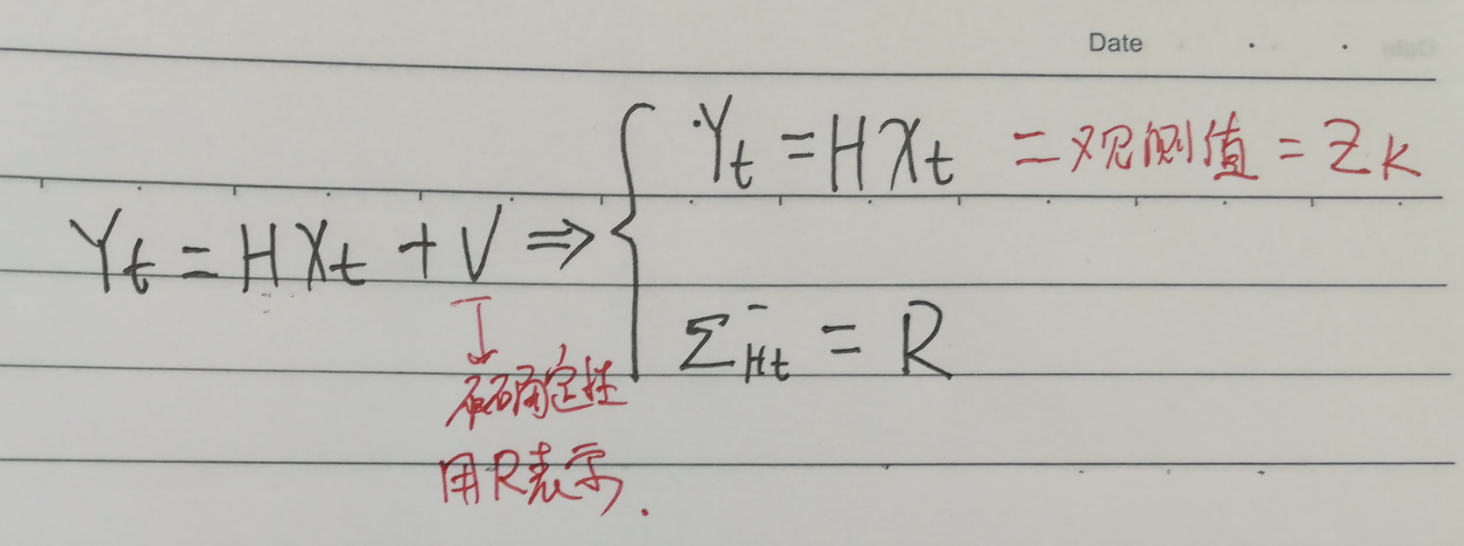
自己的探测（量测、测量）信息给用户做参考，其可以用这个公式表示：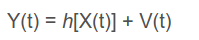
，借用参考链接4的表述：
----------------
---------------------------
这时后，我们就要开始分析了，如何将观测信息和估计值进行融和。我们的目的是求车辆位置xt的状态，
那么，根据估计值有：
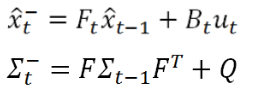
那么，根据观测值有：
我们，对观测值，按估计值那样整理，并且得到
假设所有的不确定都是服从高斯分布的，然后，从上面的两个式子可以理解为：
对于估计值，它是对下一状态的估计，均值为
，方差为：sqrt（
），其图像为：
但是，这里有一个问题，我们的
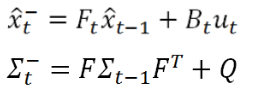的高斯是关于位置的高斯，要和传感器融和，需要转换到传感器上，转换成传感器的高斯：
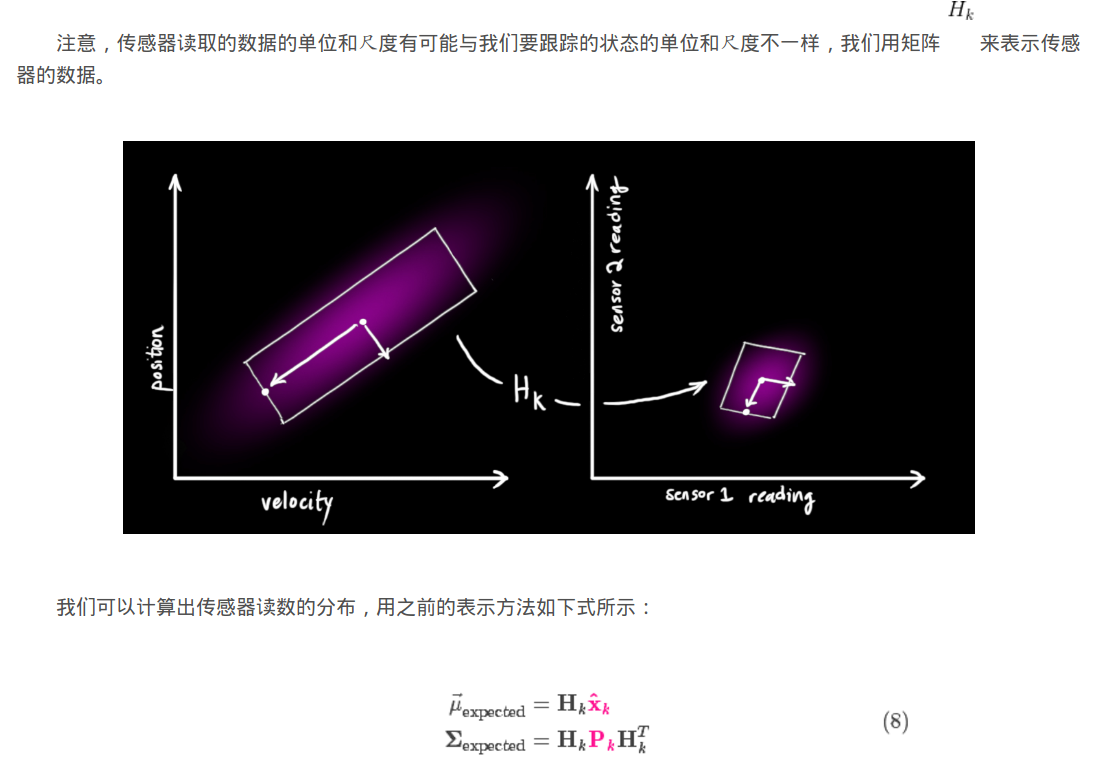
对于测量（观测、量测）值，同样是高斯，其均值为：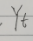
，方差为sqrt（
），图像为：
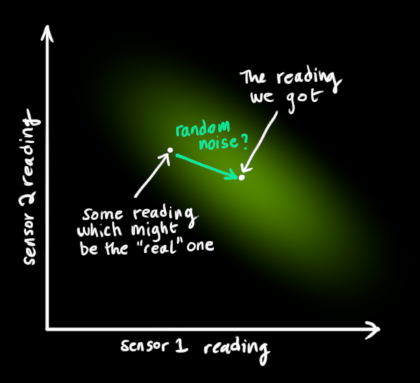
这时候，我们分析，举个例子，
小红的成绩不低于90分（这是估计值），老师看了所有人的试卷，说，最高分不超过98分（这是观测值），那么小红成绩猜测是多少？
我们通过估计和观测值知道，小红的成绩是y 范围在[90,98],之间，做出估计就取平均值：（90+98）/2 = 94分。
同样的，在参考1中的描述为：
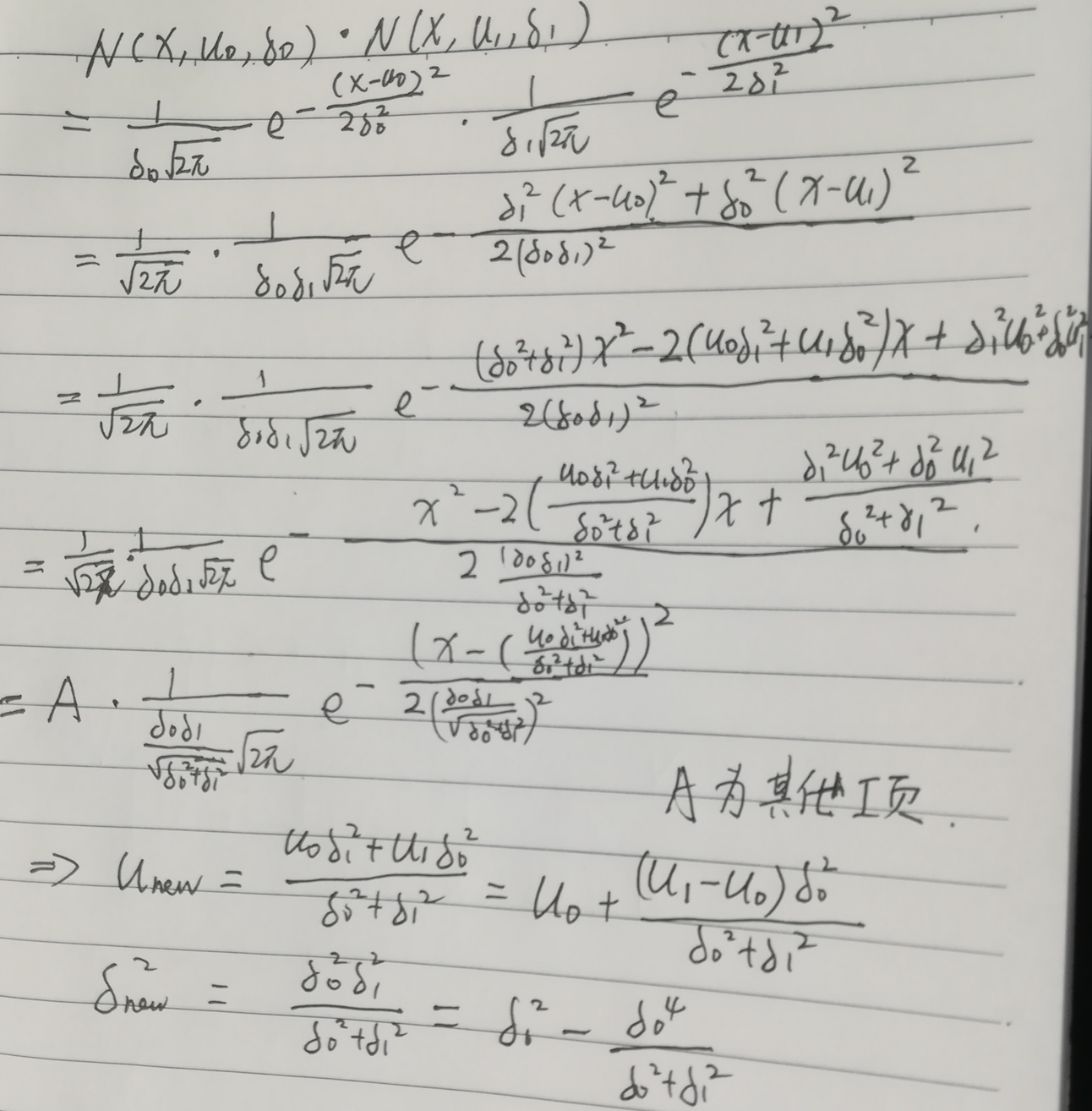
其中：
= 
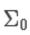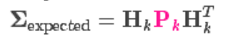因为是从估计值转换到传感器读书上的预测。
= 
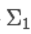按参考链接1的处理，展开：
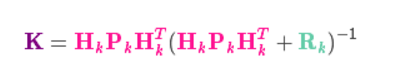
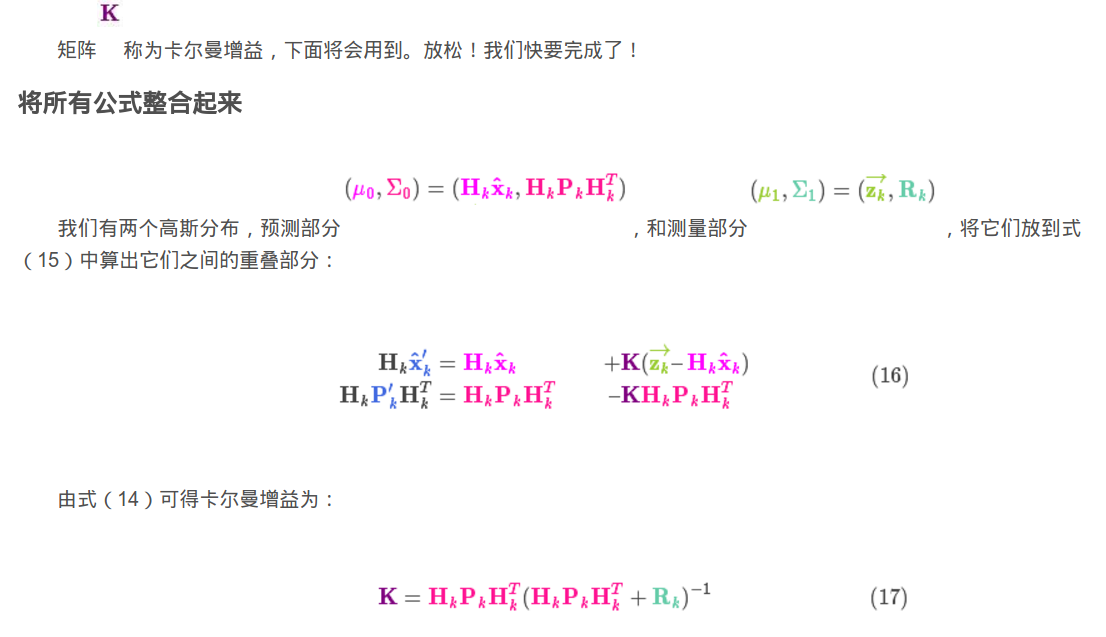
但是，我们求的是位置信息，且上面的Hk可以约掉，将传感信息，再转换为位置信息，从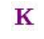
变化为
的过程。
支撑，卡尔曼的后面三个公式也推倒出来
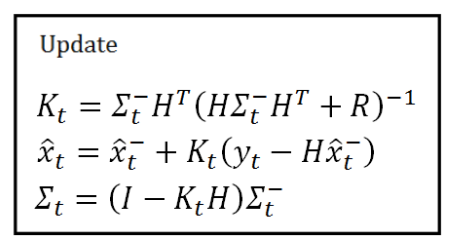
总结（个人参考和整理等总结的不成熟的解释）：
如下图所示，我们给定初始值：
- X初始状态
- Sigma 初始状态协方差矩阵
- F 状态转移矩阵
- Q 状态转移协方差矩阵
- H 观测矩阵
- R 观测噪声方差
给定这些值后，开始进入卡尔曼跟踪：
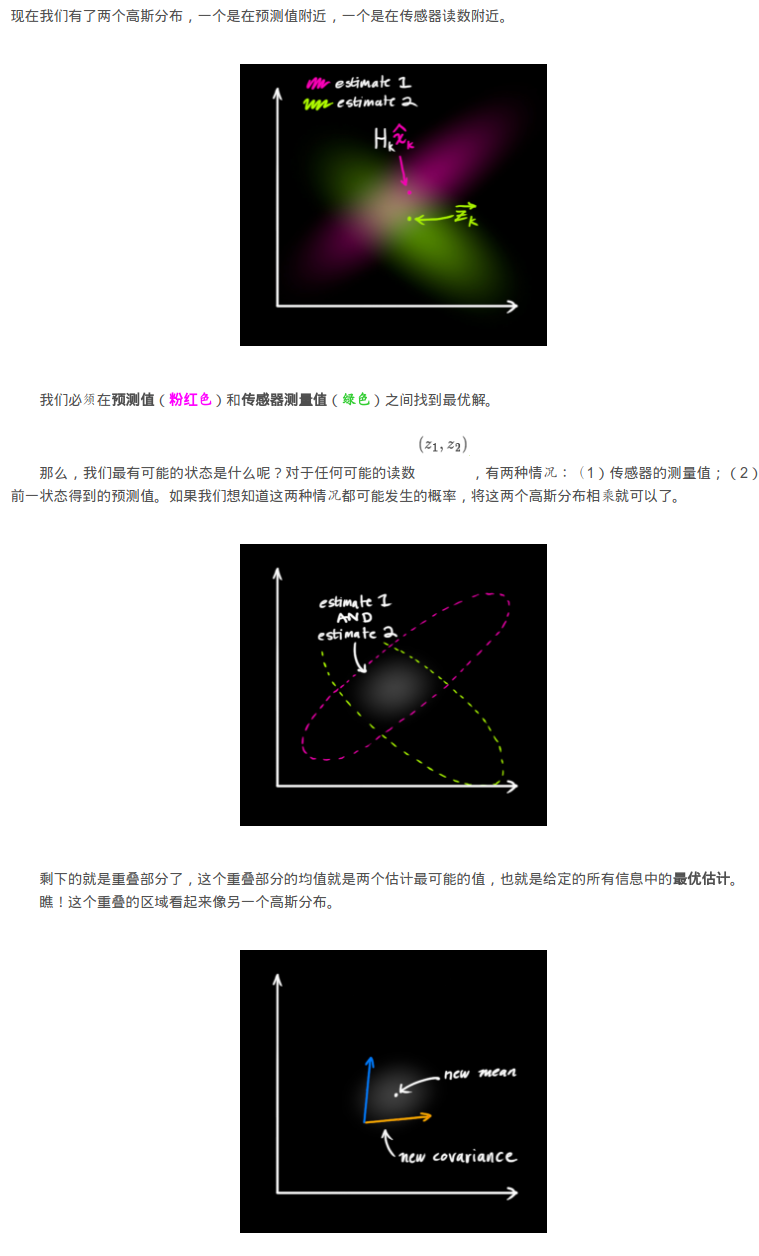
首先，通过初始值和前两个公式获得下一个时刻的位置、不确定的预测。然后，获得卡尔曼增益K，再获得下一时刻的融和值（最终值），
接着修正方差。其内在的工作机制是将观测和估计进行融和，内在原理是取两个高斯分布的交集，因为交集的误差比小于等于任何单个集合
的误差，从而获得更加精准的结果。（是否是越多传感器越好呢？？），同时，这也提供了多个传感器的融和方案。（附图来源参考链接1）
暂时写到这里吧，后面还有jpda、ekf等等
