统计学习方法 李航---第8章 提升方法
第8章提升方法
提升(boosting)方法是一种常用的统计学习方法,应用广泛且有效。在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。
基本思想:对于分类问题而言,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)要比求精确的分类规则(强分类器)容易得多。提升方法就是从弱学习算法出发,反复学习,得到一系列弱分类器(又称为基本分类器),然后组合这些弱分类器,构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布(训练数据的权值分布),针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。
8.1 提升方法AdaBoost(AdaptiveBoosting)算法
对提升方法来说,有两个问题需要回答:一是在每一轮如何改变训练数据的权值或概率分布;二是如何将弱分类器组合成一个强分类器。
关于第1个问题,AdaBoost的做法是,提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。这样一来,那些没有得到正确分类的数据,由于其权值的加大而受到后轮的弱分类器的更大关注。于是,分类问题被一系列的弱分类器“分而治之”。
至于第2个问题,即弱分类器的组合,AdaBoost采取加权多数表决的方法。具体地,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。

算法步骤说明:
步骤2 (b) 表明Gm(x)在加权的训练数据集上的分类误差率是被Gm(x)误分类样本的权值之和,由此可以看出数据权值分布Dm与基本分类器Gm(x)的分类误差率的关系。
步骤2 (c)可知,当em<=1/2时,am>=0,并且am随着em的减小而增大,所以分类误差率越小的基本分类器在最终分类器中的作用越大。
(d) 更新训练数据的权值分布为下一轮作准备,式(8.4}可以写成
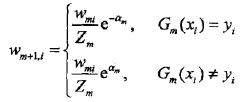
由此可知,被基本分类器Gm(x)误分类样本的权值得以扩大,而被正确分类样本的权值却得以缩小。.两相比较,误分类样本的权值被放大。
不改变所给的训练数据,而不断改变训练数据权值的分布,使得训练数据在基本分类器的学习中起不同的作用,这是AdaBoost的一个特点.
步骤(3) 所有系数am之和并不为1。利用基本分类器的线性组合构建最终分类器是AdaBoost的另一特点。
8.2 AdaBoost算法的训练误差分析
定理8.1 (AdaBoost的训练误差界) AdaBoost算法最终分类器的训练误差界为
这一定理说明,可以在每一轮选取适当的Gm使得Zm最小,从而使训练误差下降最快。对二类分类问题,有如下结果:
定理8.2(二类分类问题AdaBoost的练误差界)
这里,rm=1/2 - em
推论8.1 如果存在r>0,对所有m有rm>=r,则

这表明在此条件下AdaBoost的训练误差是以指数速率下降的。
注意,AdaBoost算法不需要知道下界r。AdaBoost具有适应性,即它能适应弱分类器各自的训练误差率。
AdaBoost的训练误差分析表明,AdaBoost的每次迭代可以减少它在训练数据集上的分类误差率,这说明了它作为提升方法的有效性。
8.3 AdaBoost算法的解释
AdaBoost算法还有另一个解释,即可以认为AdaBoost算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法时的二类分类学习方法。
前向分步算法(forward stagewise algorithm)
加法模型:
![]()

其中,b为基函数,r为基函数的参数,beta为基函数的系数。
前向分步算法同时求解从m=1到M所有参数的优化问题简化为逐次求解各个参数的优化问题.

前向分步算法与AdaBoost是等价的。
定理8.3 AdaBoost算法是前向分步加法算法的特例。这时,模型是由基本分类器组成的加法模型,损失函数是指数函数。
8.4 提升树
提升树是以分类树或回归树为基本分类器的提升方法。提升树被认为是统计学习中性能最好的方法之一。
提升树模型
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。
基本分类器x<v或x>v,可以看作是由一个根结点直接连接两个叶结点的简单决策树,即所谓的决策树桩(decision stump)。
提升树模型可以表示为决策树的加法模型:
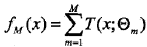
其中,T表示决策树,theta为决策树的参数,M为树的个数。
提升树算法
提升树算法采用前向分步算法。首先确定初始提升树f0(x)=0,第m步的模型是

其中,fm-1(x)为当前模型,通过经验风险极小化确定下一棵决策树的参数。

不同问题的提升树学习算法主要区别在于使用的损失函数不同。包括用平方误差损失函数的回归问题,用指数损失函数的分类问题,以及用一般损失函数的一般决策问题。
对于二类分类问题,提升树算法只需将AdaBoost算法8.1中的基本分类器限制为二类分类树即可,是AdaBoost算法的特殊情况。
回归问题的提升树算法
当采用平方误差损失函数时,

在前向分步算法的第m步,损失变为,

其中![]() 是当前模型拟合数据的残差(residual)。
是当前模型拟合数据的残差(residual)。
所以对回归问题的提升树算法来说,求解经验风险极小化的问题只需简单地拟合当前模型的残差。

梯度提升算法
提升树利用加法模型与前向分步算法实现学习的优化过程。当损失函数是平方损失和指数损失函数时。每一步优化是很简单的。但对一般损失函数而言,往往每一步优化并不那么容易。针对这一问题,Freidmao提出了梯度提升(gradient boosting)算法。这是利用最速下降法的近似方法,其关键是利用损失函数的负梯度在当前模型的值

作为回归问题提升树算法中的残差的近似值,拟合一个回归树。

算法第1步初始化,估计使损失函数极小化的常数值,它是只有一个根结点的树,即 x>c 和 x<c;
第2 (a)步计算损失函数的负梯度在当前模型的值,将它作为残差的估计。对于平方损失函数,它就是通常所说的残差;对于一般损失函数,它就是残差的近似值。
第2 (b)步估计回归树叶结点区域,以拟合残差的近似值
第2 (c)步利用线性搜索估计叶结点区域的值,使损失函数极小化
第2 (d)步更新回归树。
第3步得到输出的最终模型。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号