关于《Differentially private empirical risk minimization》论文分析报告
Differentially private empirical risk minimization——分析报告
组员:岑鹏 吴易佳 秦红梅
2020.3.12
1. 背景
随着电子数据库中的个人信息的大量增加,例如病历,财务记录,网络搜索历史记录和社交网络数据等,互联网进入了大数据时代,为了利用其中海量的有价值的数据信息,不可避免地需要对数据进行收集和分析,使得隐私泄露问题变得越来越严重,数据隐私保护已经成为目前关注的焦点。数据挖掘以及信息安全技术的不断发展,对数据进行简单地匿名化或者公布敏感数据集的统计信息不足以保护隐私,而隐私计算和数据加密技术也不能满足大数据隐私保护的要求,2006年DWork针对统计数据库的隐私泄露问题提出了差分隐私技术,其模型建立在严格的数学基础之上,能够抵御合成攻击,并保证数据的极大可用性。目前差分隐私已被广泛应用于安全领域。本文主要以隐私保护的方式研究具有正则化ERM学习分类器的问题。
2. Differential Privacy & ERM
2.1Differential Privacy
差分隐私是Dwork在2006年提出的一种针对机器学习敏感数据集发布导致的隐私泄露问题的隐私保护模型。基于这一模型,处理后的数据集对任意一个记录的变化是不敏感的,因此一个数据记录在数据集中是否存在对于统计计算结果的影响非常小。攻击者无法通过观察计算结果而获取准确的个体信息,因为一条记录加入数据集而产生的隐私泄露风险被控制在可接受的范围内。
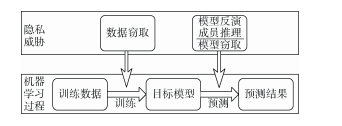
图1 模型训练中的隐私威胁
例如:有两个数据集分别为D和D',D和D'之间只有一条记录是不同的,其他记录都是相同的。数学描述为|D△D'|=1。然后对D和D'两个数据集进行查询操作,比如操作1为查询D中99个用户的记录,操作2为查询D'中100个用户的记录,如果操作1返回的结果和操作2返回的结果一模一样(一模一样是理想状态,实际上只要接近就好,具体实施的时候会有一个隐私预算,只要低于某个阈值就ok),那么就是完美的保护了用户隐私。这句话的意思其实是说,既然查询99个人的记录和查询100个人的记录返回的结果一致,那么第100个人就很乐意的奉献自己的隐私数据,反正有我没我攻击者查询得到的结果都是一样的。
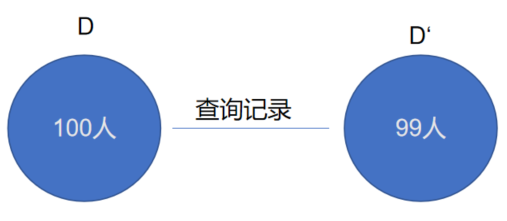
图2 对两个数据集进行查询
设有随机算法M,PM为所有可能输出构成的集合的概率,对于任意两个领近数据集D与D',若算法满足:
![]()
则称算法M提供了ε-差分隐私保护。通常情况下,ε越小,eε越接近1,两个的概率就越接近,那么保密程度越高。相反,如果ε越大,那么隐私保护的越不好,凡是查询的结果会比较准确(error较小)。
2.2ERM
2.2.1 经验风险最小化
经验风险最小化的策略认为,经验风险最小的模型是最优的模型:
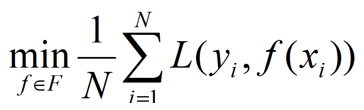
当样本容量足够大时,经验风险最小化能保证有很好的学习效果。比如,极大似然估计(就是经验风险最小化的一个例子,当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化就等价于极大似然估计)。但当样本容量很小时,经验风险最小化容易导致“过拟合”。
2.2.2 结构风险最小化
结构风险最小化(structural minimization, SRM)是为了防止过拟合提出的策略。结构风险最小化等价于正则化(regularization)。结构风险在经验风险上加上表示模型复杂度的正则化项(regularizer)或罚项(penalty term)。结构风险的定义是:
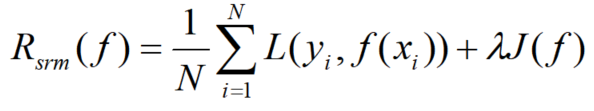
其中J(f)是模型复杂度的函数,是系数,用来权衡经验风险和模型复杂度。结构风险最小化的策略认为结构风险最小的模型是最优模型:
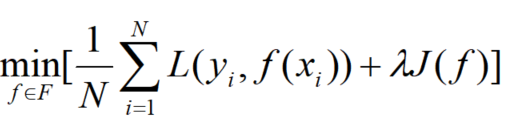
结构风险小需要经验风险和模型复杂度同时都小,结构风险小的模型往往对训练数据以及未知的测试数据都有较好的预测。比如,贝叶斯估计中的最大后验概率估计(maximum posterior probability estimation,MAP)就是结构风险最小化的一个例子,当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化就等价于最大后验概率估计。
3. 算法介绍
本文主要介绍了Dwork(2006)提出的sensitivity method和作者提出的objective perturbation.
3.1输出扰动
思想:在function的输出中添加一个噪声b

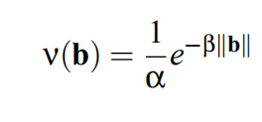
具体流程:

通过在输出结果中添加噪声能起到一定的伪装作用。但有一个缺点,在某些特定的应用情况下,function的灵敏度会比较高,这时候需要添加一个高方差的噪声。
为什么添加高方差的噪声?
因为灵敏度高代表分散的比较开,function不平滑,这时候就需要通过减小方差来解决。但这里是为了配合这种离散程度高,所以要添加一个高方差的noise。
3.2目标扰动
思想:通过在目标函数添加噪声来达到目的

添加噪声后的function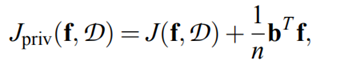
PS:该方法中隐私参数不依赖分类算法的灵敏度。
具体流程:

算法中的第一步是对ε的逼近,因为隐私保护中ε值越小,代表保护的越好。
4. 实验
作者分别在两个数据集中对两种算法进行测试(从两个方面)。
两种分类器:logistic regression & SVM
4.1 Privacy-Accuracy Trade-off
针对添加隐私保护对于算法的准确性进行一个测试。
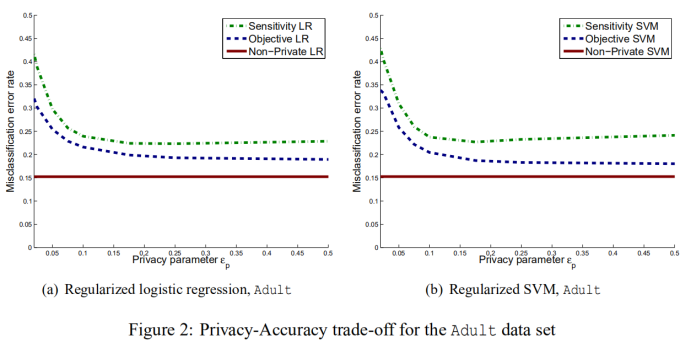
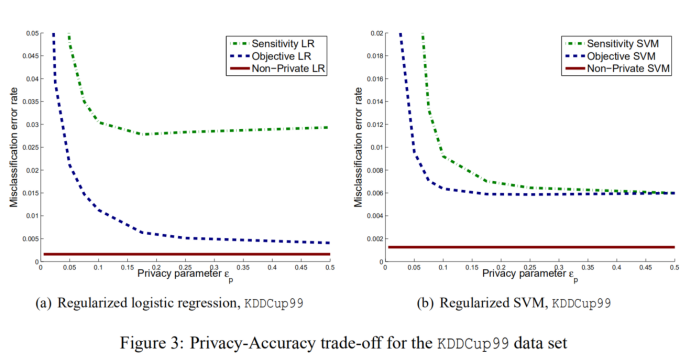
从实现结果中可以看出,目标扰动比输出扰动表现得更好,并且支持向量机的目标扰动比逻辑回归的目标扰动具有更低的分类误差。
4.2 Accuracy vs. Training Data Size Tradeoffs
研究分类精度如何随着训练集的大小而变化。
由于Adult数据集数量不够,这次实验只选择了KDDCup99数据集进行实验。
实验准备:
训练集从60000至120000,验证和测试套各为25000。隐私保护率ε分别设为0.05和0.01进行实验。
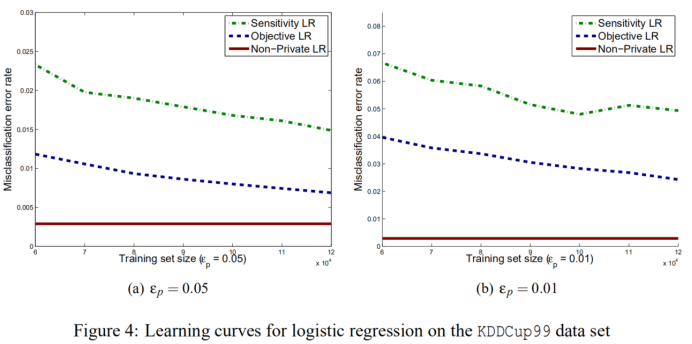
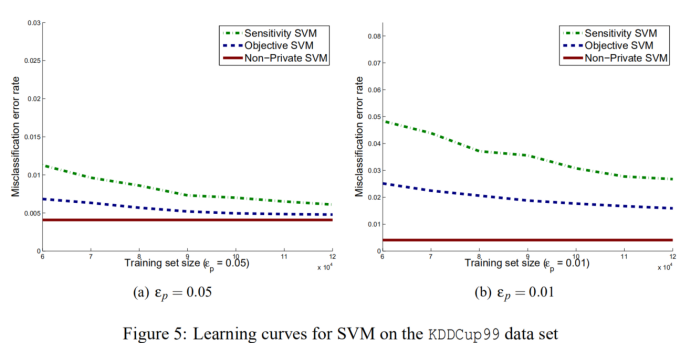
图4和图5分别给出了目标扰动、输出扰动和标准Logistic损失的灵敏度方法的学习曲线。
从图中看到,对于标准Logistic回归和SVM进行学习,随着数据大小的增加,误差保持不变。 对于两种隐私保护方法,误差通常会减小。在所有情况下,目标扰动都优于灵敏度方法,SVM通常优于Logistic回归。
5. 总结
本文在Dwork等人的–差分隐私模型中考虑隐私保护,提供了两种隐私保护的ERM算法,第一种是在不加隐私保护算法的输出中添加了噪声的敏感度方法,,第二种是在目标函数中添加噪声的目标扰动方法,并且为实现泛化误差提供了算法的样本需求界限,以及算法中联合核方法的应用,最后在两个真实数据集上提供了两种算法的实验。对于分类,随着隐私保护的更加严格,错误率会增加,实验结果表明,在保护隐私和学习效果的平衡上,目标扰动通常优于敏感度方法,两种算法在有更多训练数据的情况下都表现得更好,并且有大量的训练数据可用时,两种算法的性能都可能接近于没有添加隐私保护而进行的分类。本文有三个问题未能得到解决,如何将目标扰动方法进一步扩展到更一般的凸优化问题以及寻找一个更好的解决方案来使用核方法进行隐私保护分类等。
6. 参考文献
[1]Kamalika Chaudhuri. Differentially private empirical risk minimization. Journal of Machine Learning Research 12 (2011) 1069-1109
[2]https://zhuanlan.zhihu.com/p/48534275




