(未完结)“文远知行杯”GDET第十四届竞赛(网络赛共10题,仅整理出6题)
刚开学没多久就打了一个网络赛,通过这次网络赛我是发现我是真的菜...
放假前校赛的排名让我有些自满,寒假丝毫没有接触ACM,一直沉迷于Steam,这个真的值得好好反省。
虽然现在大一课有点多,在学校也有些事务,但是这些都不是我松懈的理由,
在此写下这篇博客就是为了提醒自己:Why(),How,What
这次比赛的反思:
数论的学习实在是太过于薄弱,要加强,对数字的规律不够敏感,要锻炼,
数据结构最常用的树,不会,要学,
这次题目总体不算特别难,题目的灵活度不大,关键自己会的知识太少。
题目链接
http://acm.hdu.edu.cn/search.php?field=problem&key=%A1%B0%D7%D6%BD%DA%CC%F8%B6%AF-%CE%C4%D4%B6%D6%AA%D0%D0%B1%AD%A1%B1%B9%E3%B6%AB%B9%A4%D2%B5%B4%F3%D1%A7%B5%DA%CA%AE%CB%C4%BD%EC%B3%CC%D0%F2%C9%E8%BC%C6%BE%BA%C8%FC&source=1&searchmode=source
HUD 6461(概率的问题)(答案4行1.00,//题目有点没说明白)
HDU 6462(斐波那契数列平方和)
题意有点看不太清楚,但是所给的数据还是很容易发现规律,
斐波那契数列每一项的平方和,把所给的4进制a,b,换成10进制就行,打个表就OK了
#include <iostream> #include <cstdio> #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)>(y)?(y):(x)) using namespace std; const int mod=192600817; const int maxn=4e4+5; long long fio[maxn]={0,1}; long long sum[maxn]={0,1}; void make_table() { for(int i=2; i<maxn; i++) { fio[i]=(fio[i-1]+fio[i-2])%mod; sum[i]=(fio[i]*fio[i])% mod+sum[i-1]; //后面是要求 sum的差值,这里的sum不要求余,可大致看一下也能发现long long 不会溢出 } } int main() { make_table(); /* for(int i=0; i<10; i++) { printf("%d %I64d %I64d\n", i , fio[i], sum[i]); } */ int Q; while(cin>>Q) { while(Q--) { int a,b,c,d; cin>>a>>b>>c>>d; a=a*4+b+1; c=c*4+d+1; b=max(a,c); d=min(a,c); cout<<(sum[b]-sum[d-1])%mod<<endl; //取余别忘记了 } } return 0; }
HDU 6463(查询第k个鸽子数)
一看就是肯定有规律,
方法1:
随便取几个数字出来,打个表(我傻傻的那笔在那里找规律,把电脑当计算器😂)看一下,都会出现那些重复的数字,
发现要么会出现4要么会出现1,然后打个表就OK了;
1 #include <iostream> 2 using namespace std; 3 4 const int maxn=150005; 5 long long table[maxn]; 6 7 bool myJudge(int n) 8 { 9 while(n!=1&&n!=4) 10 { 11 int sum=0; 12 while(n) 13 { 14 sum+=(n%10)*(n%10); 15 n/=10; 16 } 17 n=sum; 18 } 19 return n==1; 20 } 21 22 void make_table() 23 { 24 int cnt=0; 25 for(int i=1; cnt<maxn; i++) 26 { 27 if(myJudge(i)) 28 table[cnt++]=i; 29 } 30 } 31 32 int main() 33 { 34 make_table(); 35 int Q; cin>>Q; 36 while(Q--) 37 { 38 int k; cin>>k; 39 cout<<table[k-1]<<endl; 40 } 41 42 return 0; 43 }
方法2:
当时感觉有循环节,确定一个大概的循环次数,超出这个次数还未有1即false,不过当时很快就找出来规律,这个就没写了
方法3:
记忆化搜索(配合set)
HDU 6464
看了不少题解都说要用 带权值的线段树,或者主席树,这个还不会,先放着,等学到这个在A了
HDU 6465(三角形的变换)
找初始三角形边的向量和变换后的边的向量,在确定一下矩阵的类型,求矩阵。
求出这个矩阵之后,对于每个给你的点,先求出它关于三角形第一个点变换之前的向量,乘上这个矩阵得到变换之后的向量,再加上三角形第一个点变换之后的坐标即可。
1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 5 int main () 6 { 7 int T; cin>>T; 8 while(T--) 9 { 10 double x[10],y[10]; 11 for(int i=1;i<=6;i++) 12 cin>>x[i]>>y[i]; 13 14 for(int i=2;i<=3;i++) 15 x[i]-=x[1],y[i]-=y[1]; 16 for(int i=5;i<=6;i++) 17 x[i]-=x[4],y[i]-=y[4]; 18 19 double a,b,c,d; 20 c=(x[5]*x[3]-x[6]*x[2])/(y[2]*x[3]-x[2]*y[3]); 21 a=(x[5]-y[2]*c)/x[2]; 22 d=(y[5]*x[3]-y[6]*x[2])/(y[2]*x[3]-x[2]*y[3]); 23 b=(y[5]-y[2]*d)/x[2]; 24 25 int Q; cin>>Q; 26 while(Q--) 27 { 28 cin>>x[2]>>y[2]; 29 x[2]-=x[1],y[2]-=y[1]; 30 printf("%.2f %.2f\n",x[2]*a+y[2]*c+x[4],x[2]*b+y[2]*d+y[4]); 31 } 32 } 33 return 0; 34 }
HDU 6466
超出的我的能力范围...
HDU 6467(数学式的简化+快速幂(这种式子化简的方法有待总结))
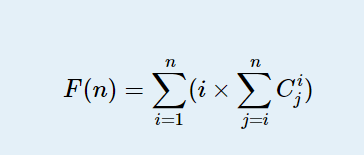
难点在于这种式子式如何化简的;
化简得F(n)=(n-1)*2^n+1;
#include <iostream> #include <cstdio> using namespace std; long long mod=1000000007; long long poww(long long a, long long b) { long long ans=1,base=a; while(b) { if(b&1) ans=(ans*base)%mod; base=(base*base)%mod; b>>=1; } return ans; } int main () { long long n; while(cin>>n) { cout<<(poww(2,n)*((n-1)%mod)+1)%mod<<endl; } return 0; }
HDU 6468 (应该是线段树划分区间或者字典树 暂时还不会,有待解决)
HDU 6469 不会
HDU 6470 (给F(n)的递推式求F(n))
给了fn的递推式,确定一下如何用矩阵表示,矩阵快速幂即可。(下图引用自csdn https://blog.csdn.net/winter2121/article/details/88612870)
发现自己有必要学习如何定义矩阵(class)以及矩阵重载运算符这些,这样的话会方便很多。
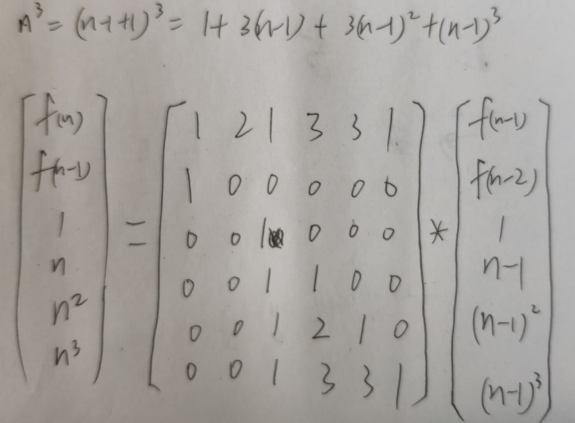
#include <iostream> #include <cstdio> using namespace std; const int mod=123456789; struct Matrix{ long long m[6][6]; }; Matrix Mul(Matrix A, Matrix B) { Matrix ans; for(int i=0; i<6; i++) for(int j=0; j<6; j++) ans.m[i][j]=0; for(int i=0; i<6; i++) for(int j=0; j<6; j++) for(int k=0; k<6; k++) ans.m[i][j]=((A.m[i][k]*B.m[k][j])%mod+ans.m[i][j])%mod; return ans; } Matrix Quick_Pow(Matrix A, long long n) { Matrix ans; for(int i=0; i<6; i++) for(int j=0; j<6; j++) { if(i==j) ans.m[i][j]=1; else ans.m[i][j]=0; } while(n) { if(n&1) ans=Mul(ans,A); A=Mul(A, A); n>>=1; } return ans; } int main() { int T; cin>>T; while(T--) { long long n; cin>>n; Matrix A; for(int i=0; i<6; i++) for(int j=0; j<6; j++) A.m[i][j]=0; A.m[0][0]=1; A.m[0][1]=2; A.m[0][2]=1; A.m[0][3]=3; A.m[0][4]=3; A.m[0][5]=1; A.m[1][0]=1; A.m[2][2]=1; A.m[3][2]=1; A.m[3][3]=1; A.m[4][2]=1; A.m[4][3]=2; A.m[4][4]=1; A.m[5][2]=1; A.m[5][3]=3, A.m[5][4]=3; A.m[5][5]=1; Matrix ans=Quick_Pow(A, n-2); long long Ans=0; long long a[6]={2,1,1,2,4,8}; /* for(int i=0; i<6; i++) for(int j=0; j<6; j++) { printf("%I64d ",A.m[i][j]); if(j==5) cout<<endl; } cout<<endl; */ for(int i=0; i<6; i++) { Ans=(Ans+(a[i]*ans.m[0][i])%mod)%mod; } cout<<Ans<<endl; /* for(int i=0; i<6; i++) for(int j=0; j<6; j++) { printf("%I64d ",ans.m[i][j]); if(j==5) cout<<endl; } */ } return 0; }




