找出游戏的必胜策略

 

---

 

游戏与必胜策略

1.硬币游戏1

• 问题描述：x枚硬币，k个数字：a₁，a₂，…，a_k，A和B轮流取硬币，每次所取的枚数一定要在a₁，a₂，…，a_k当中，A先取，取走最后一枚硬币的一方获胜。当双方都采取最优策略时，谁会获胜？假定a₁，a₂，…，a_k当中一定有1
• 限制条件：
  1≤x≤10000
  1≤k≤100
  1≤a_i≤x
• 分析：
  考虑当轮到自己时，还有j枚硬币时的胜负情况
  ①题目规定取光所有的硬币就获胜，这等价于轮到自己时如果没有硬币了就失败了。因此，j=0时是必败态。
  ②如果对于某个i(1≤i≤k)，j-a_i是必败态的话，j就是必胜态。（如果当前有j枚硬币，只要取走a_i枚对手就必败→自己必胜）
  ③如果对于任意的i(1≤i≤k)，j-a_i都是必胜态的话，j就是必败态。（不论怎么取，对手都必胜→自己必败）
  根据这些规则，我们就能利用动态规划算法按照j从小到大的顺序计算必胜态必败态。只要看x是必胜态还是必败态，就能知道谁会获胜了。
  通过考虑各个状态的胜负条件，判断必胜态和必败态，是有胜败的游戏的基础。
• 代码：

---

 

2.A Funny Game(POJ 2484)

• 原题如下:
  A Funny Game

  Time Limit: 1000MS	Memory Limit: 65536K
  Total Submissions: 7028	Accepted: 4408

  Description

  Alice and Bob decide to play a funny game. At the beginning of the game they pick n(1 <= n <= 10⁶) coins in a circle, as Figure 1 shows. A move consists in removing one or two adjacent coins, leaving all other coins untouched. At least one coin must be removed. Players alternate moves with Alice starting. The player that removes the last coin wins. (The last player to move wins. If you can't move, you lose.)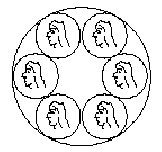 
  
  Figure 1
  Note: For n > 3, we use c1, c2, ..., cn to denote the coins clockwise and if Alice remove c2, then c1 and c3 are NOT adjacent! (Because there is an empty place between c1 and c3.) 
  
  Suppose that both Alice and Bob do their best in the game. 
  You are to write a program to determine who will finally win the game.

  Input

  There are several test cases. Each test case has only one line, which contains a positive integer n (1 <= n <= 10⁶). There are no blank lines between cases. A line with a single 0 terminates the input. 

  Output

  For each test case, if Alice win the game,output "Alice", otherwise output "Bob". 

  Sample Input

  1
  2
  3
  0
  

  Sample Output

  Alice
  Alice
  Bob

• 分析：
  n高达1000000，考虑到还有将连续部分分裂成几段等的情况，状态数非常地多，搜索和动态规划都难以胜任。需要更加巧妙地判断胜败关系。
  首先，如果能把所有的硬币分成两个完全相同的组的状态，必败态显然。不论自己采取什么选取策略，对手只要在另一组采取相同的策略，就又回到了分成两个相同的组的状态，不断这样循环下去，总会在某次轮到自己时没有硬币了。也就是说，因为对手取走了最后一枚硬币而败北。
  接下来，回到正题，Alice在第一步取走了一枚或两枚硬币，原本成圈的硬币就变成了长度为n-1或n-2的链，这样只要Bob在中间位置，根据链长的奇偶性，取走一枚或两枚硬币，就可以把所有硬币正好分成了两个长度相同的链。这正如之前讨论过的，是必败态，也就是说Alice必败，Bob必胜。只不过，当n≤2时，Alice可以在第一步取光，所以胜利的是Alice。
• 注：在这类游戏当中，作出对称的状态后再完全模仿对手的策略常常是有效的。
• 代码：

  #include<cstdio>
  #include<algorithm>
  
  using namespace std;
  
  int main()
  {
      int n;
      while (scanf("%d", &n))
      {
          if (n==0) break;
          if (n<=2) puts("Alice");
          else puts("Bob");
      }
  }

---

 

3.Euclid's Game(POJ 2348)

• 原题如下：
  Euclid's Game

  Time Limit: 1000MS	Memory Limit: 65536K
  Total Submissions: 10754	Accepted: 4386

  Description

  Two players, Stan and Ollie, play, starting with two natural numbers. Stan, the first player, subtracts any positive multiple of the lesser of the two numbers from the greater of the two numbers, provided that the resulting number must be nonnegative. Then Ollie, the second player, does the same with the two resulting numbers, then Stan, etc., alternately, until one player is able to subtract a multiple of the lesser number from the greater to reach 0, and thereby wins. For example, the players may start with (25,7): 
  

           25 7
  
           11 7
  
            4 7
  
            4 3
  
            1 3
  
            1 0

  
  an Stan wins.

  Input

  The input consists of a number of lines. Each line contains two positive integers giving the starting two numbers of the game. Stan always starts.

  Output

  For each line of input, output one line saying either Stan wins or Ollie wins assuming that both of them play perfectly. The last line of input contains two zeroes and should not be processed.

  Sample Input

  34 12
  15 24
  0 0
  

  Sample Output

  Stan wins
  Ollie wins

• 分析：找该问题中必胜态和必败态的规律。
  首先，如果a>b则交换，假设a<b，另外，如果b已经是a的倍数了则必胜，所以假设b并非a的倍数。
  此时，a和b的关系，按自由度的观点，可以分成一下两类。
  ① b-a<a的情况
  ② b-a>a的情况
  对于第一种情况，只能从b中减去a，而第二种情况则有多种选择。
  对于第一种情况，判断必胜还是必败比较简单，如果b减去a之后所得到的状态是必败态的话，它就是必胜态，如果得到的是必胜态的话它就是必败态。
  对于第二种情况，假设x是使得b-ax<a的最小整数，考虑b-a(x-1)的情况。此时，接下来的状态就成了前边讲过的没有选择余地的第一种情况。如果该状态是必败态的话，当前状态就是必胜态。那么，如果减去a(x-1)后的状态是必胜态的话，怎么办？此时，b-ax的状态是b-a(x-1)后的状态唯一可以转移到的状态，根据假设，b-a(x-1)后的状态是必胜态，所以b-ax后的状态是必败态，那么当前状态就是必胜态。由此可知，第二种情况总是必胜的。所以，从初状态开始，最先达到有自由度的第二种状态的一方必胜。
• 代码：

  #include<cstdio>
  #include<algorithm>
  
  using namespace std;
  
  void swap(int &a, int &b)
  {
      int t=a;
      a=b;
      b=t;
  }
  
  int main()
  {
      int a, b;
      while (scanf("%d %d", &a, &b))
      {
          if (a==0 && b==0) break;
          bool f=true;
          for (;;)
          {
              if (a>b) swap(a, b);
              if (b%a==0) break;
              if (b-a>a) break;
              b-=a;
              f=!f;
          }
          if (f) puts("Stan wins");
          else puts("Ollie wins");
      }
  }

---

 

Nim

1.Nim

• 问题描述：有n堆石子，每堆各有a_i颗石子，Alice和Bob轮流从非空的石子堆中取走至少一颗石子，Alice先取，取光所有石子的一方获胜。问当双方都采取最优策略时，谁会先获胜？
• 限制条件：
  1≤n≤1000000
  1≤a_i≤10⁹
• 分析：判断该游戏的策略只要用异或运算就好了。有以下结论成立：
  a₁ xor a₂ xor … xor a_n ≠ 0 → 必败态
  a₁ xor a₂ xor … xor a_n = 0 → 必胜态
  因此只要计算异或值，非零就是Alice必胜，为零就是Bob必胜。
  简略证明：
  首先，一旦从xor为零的状态取走至少一颗石子，xor就一定会变成非零，因此，可以证实必败态只能转移到必胜态
  接下来，我们证明必败态总是能转移到某个必败态，观察XOR的二进制表示最高位的1，选取石子数的二进制表示对应位也为1的某堆石子，只要从中取走使得该位变为0，且其余xor中的1也反转的数量的石子，xor就可以变成零。

---

 

2.Georgia and Bob(POJ 1704) 【这个问题又被称为Staircase Nim】

• 原题如下：
  Georgia and Bob

  Time Limit: 1000MS	Memory Limit: 10000K
  Total Submissions: 12567	Accepted: 4205

  Description

  Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: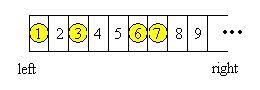 
  
  Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game. 
  
  Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out. 
  
  Given the initial positions of the n chessmen, can you predict who will finally win the game? 

  Input

  The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

  Output

  For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

  Sample Input

  2
  3
  1 2 3
  8
  1 5 6 7 9 12 14 17
  

  Sample Output

  Bob will win
  Georgia will win

• 分析：如果将棋子两两成对当成整体来考虑，就可以把这个游戏转为Nim游戏。如果棋子个数为偶数，把棋子从前往后两两组成一对，可以将每对棋子看成Nim中的一堆石子，石子的个数等于两个棋子之间的间隔。将右边的棋子向左移就相当于从Nim的石子堆中取走石子，将左边的棋子向左移，石子的数量增加了，这和Nim不同，但即便对手增加了石子的数量，只要将所加部分减回去就回到了原来的状态。因此，该游戏的胜负状态和所转移成的Nim的胜负状态一致。
• 代码：

  #include<cstdio>
  #include<algorithm>
  
  using namespace std;
  
  const int MAX_N=1000;
  int T, N, P[MAX_N];
  
  int main()
  {
      scanf("%d", &T);
      while (T>0)
      {
          T--;
          scanf("%d", &N); 
          for (int i=0; i<N; i++)
          {
              scanf("%d", &P[i]);
          }
          if (N%2==1) P[N++]=0;
          sort(P, P+N);
          int x=0;
          for (int i=0; i+1<N; i+=2)
          {
              x ^= (P[i+1]-P[i]-1);
          }
          if (x==0) puts("Bob will win");
          else puts("Georgia will win");
      }
  }

---

 

Grundy数

1.硬币游戏2

• 问题描述：给定k个数字a1，a2，…，a_k。有n堆硬币，每堆各有x_i枚硬币，Alice和Bob轮流选出一堆硬币，从中取出一些硬币，每次所取硬币的枚数一定要在a₁，a₂，…，a_k当中。Alice先取，取光硬币的一方获胜。当双方都采取最优策略时，谁会获胜？保证a1，a2，…，a_k中一定有1。
• 限制条件：
  1≤n≤1000000
  1≤k≤100
  1≤x_i，a_i≤10000
• 分析：利用Grundy值，许多游戏都可以转成前面所介绍的Nim
  考虑一下只有一堆硬币的情况，硬币枚数x所对应的Grundy值的计算方法如下：

  int grundy(int x)
  {
      集合 S={};
      for (j=1, ... ,k)
      {
          if (a_j<=x) 将grundy(x-a_j)加到S中 
      }
      return 最小的不属于S的非负整数 
  }

   也就是说，当前状态的Grundy值就是除任意一步所能转移到的状态的Grundy值以外的最小非负整数。这样的Grundy值，和Nim中的一个石子堆类似，有如下性质
  ① Nim中有x颗石子的石子堆，能够转移成有0，1，…，x-1颗石子的石子堆
  ② 从Grundy值为x的状态出发，可以转移到Grundy值为0，1，…，x-1的状态
  和Nim不同的是，转移后的Grundy值也有可能增加，不过，对手总能够选取合适的策略再转移回相同的Grundy值的状态，所以对胜负没有影响。
  另，上面的程序是单纯递归，改成动态规划或者记忆化搜索之后，就能保证求解的复杂度为O(xk).
  了解了一堆硬币的Grundy值的计算方法之后，就可以将它看作Nim中的一个石子堆，Nim中我们用如下方法判断胜负：
  所有石子堆的石子数x_i的xor为零则必败，否则必胜
  Grundy值等价于Nim中的石子数，所以对于Grundy值的情况，有：
  所有硬币堆的Grundy值的xor为零则必败，否则必胜
  不光是这个游戏，在许多游戏中，都可以根据“当前状态的Grundy值等于除任意一步所能转移到的状态的Grundy值以外的最小非负整数”这一性质，来计算Grundy值，再根据xor来判断胜负。

• 代码：

  #include<cstdio>
  #include<algorithm>
  #include<set>
  
  using namespace std;
  
  const int MAX_N=1000000;
  const int MAX_K=100;
  const int MAX_X=10000;
  int N, K, X[MAX_N], A[MAX_K];
  int grundy[MAX_X+1];
  
  int main()
  {
      scanf("%d %d", &N, &K);
      for (int i=0; i<N; i++)
      {
          scanf("%d", &X[i]);
      }
      for (int i=0; i<K; i++)
      {
          scanf("%d", &A[i]);
      }
      grundy[0]=0;
      int max_x=*max_element(X, X+N);
      for (int j=1; j<=max_x; j++)
      {
          set<int> S;
          for (int i=0; i<K; i++)
          {
              if (A[i]<=j) S.insert(grundy[j-A[i]]);
          }
          int g=0;
          while (S.count(g)!=0) g++;
          grundy[j]=g;
      }
      int x=0;
      for (int i=0; i<N; i++) x^=grundy[X[i]];
      if (x!=0) puts("Alice");
      else puts("Bob");
  }

---

 

2.Cutting Game(POJ 2311)

• 原题如下：
  Cutting Game

  Time Limit: 1000MS		Memory Limit: 65536K
  Total Submissions: 5643		Accepted: 2060

  Description

  Urej loves to play various types of dull games. He usually asks other people to play with him. He says that playing those games can show his extraordinary wit. Recently Urej takes a great interest in a new game, and Erif Nezorf becomes the victim. To get away from suffering playing such a dull game, Erif Nezorf requests your help. The game uses a rectangular paper that consists of W*H grids. Two players cut the paper into two pieces of rectangular sections in turn. In each turn the player can cut either horizontally or vertically, keeping every grids unbroken. After N turns the paper will be broken into N+1 pieces, and in the later turn the players can choose any piece to cut. If one player cuts out a piece of paper with a single grid, he wins the game. If these two people are both quite clear, you should write a problem to tell whether the one who cut first can win or not.

  Input

  The input contains multiple test cases. Each test case contains only two integers W and H (2 <= W, H <= 200) in one line, which are the width and height of the original paper.

  Output

  For each test case, only one line should be printed. If the one who cut first can win the game, print "WIN", otherwise, print "LOSE".

  Sample Input

  2 2
  3 2
  4 2
  

  Sample Output

  LOSE
  LOSE
  WIN

• 分析：这种会发生分割的游戏，也可以计算Grundy值
  当w*h的纸张分成两张时，假设所分得的纸张的Grundy值分别为g₁和g₂，则这两张纸对应的状态的Grundy值可以表示为g₁ xor g₂。
  在Nim中，不论有几堆石子，初始状态是怎样的，只要xor的结果相同，那么对胜负是没有影响的。这里也是同样的，只要Grundy值相同，即便发生分割，只要对分割后的各部分取xor，就可以用这一个Grundy值来代表几个游戏复合而成的状态，Grundy值也可以同样计算（也可以说，这是因为xor运算的结合律）。
  另，切割纸张时，一旦切割出了长或宽为1的纸张，下一步就一定能够切割出1*1的纸张，所以可以知道此时必败。因此，切割纸张时，总要保证长和宽至少为2（无论如何都不能保证时，就是必败态。此时根据Grundy值的定义，不需要特别处理其Grundy值也是0）。
• 代码：

  #include<cstdio>
  #include<cstring>
  #include<set>
  
  using namespace std;
  
  const int MAX_WH=200;
  int w, h;
  int men[MAX_WH+1][MAX_WH+1];
  
  int grundy(int w, int h)
  {
      if (men[w][h]!=-1) return men[w][h];
      set<int> S;
      for (int i=2; w-i>=2; i++) S.insert(grundy(i, h) ^ grundy(w-i, h));
      for (int i=2; h-i>=2; i++) S.insert(grundy(w, i) ^ grundy(w, h-i));
      int res=0;
      while (S.count(res)) res++;
      return men[w][h]=res;
  }
  
  int main()
  {
      memset(men, -1, sizeof(men));
      while (~scanf("%d %d", &w, &h))
      {
          if (grundy(w, h)!=0) puts("WIN");
          else puts("LOSE");
      }
  }