numpy、scipy、pandas、matplotlib的读书报告
numpy、scipy、pandas、matplotlib的读书报告:
一、基本函数的用法
numpy
numpy是Python中用于进行科学计算的基础模块,它提供了高效的多维数组对象ndarray,以及相关的数学运算和线性代数函数。numpy的主要功能有:
- 创建和操作多维数组,如使用
np.array(),np.arange(),np.zeros(),np.ones(),np.reshape()等函数。 - 对数组进行索引和切片,如使用
a[i],a[i,j],a[:,j],a[i:j:k]等语法。 - 对数组进行数学运算,如使用
+,-,*,/,**,np.dot(),np.sin(),np.exp()等函数或运算符。 - 对数组进行统计分析,如使用
np.sum(),np.mean(),np.std(),np.min(),np.max(),np.argmin(),np.argmax()等函数。 - 对数组进行排序,如使用
np.sort(),np.argsort(),np.partition(),np.argpartition()等函数。 - 对数组进行广播,即根据一定的规则,使得不同形状的数组可以进行运算。
- 对数组进行线性代数运算,如使用
np.linalg.inv(),np.linalg.det(),np.linalg.eig(),np.linalg.solve()等函数。
scipy
scipy是基于numpy的一个科学计算库,它提供了更多的高级函数和模块,涵盖了优化,积分,插值,傅里叶变换,信号处理,图像处理,常微分方程等领域。scipy的主要功能有:
- 使用
scipy.optimize模块进行优化,如使用scipy.optimize.minimize(),scipy.optimize.curve_fit(),scipy.optimize.root()等函数。 - 使用
scipy.integrate模块进行积分,如使用scipy.integrate.quad(),scipy.integrate.odeint(),scipy.integrate.solve_ivp()等函数。 - 使用
scipy.interpolate模块进行插值,如使用scipy.interpolate.interp1d(),scipy.interpolate.splrep(),scipy.interpolate.splev()等函数。 - 使用
scipy.fftpack模块进行傅里叶变换,如使用scipy.fftpack.fft(),scipy.fftpack.ifft(),scipy.fftpack.fftshift()等函数。 - 使用
scipy.signal模块进行信号处理,如使用scipy.signal.convolve(),scipy.signal.correlate(),scipy.signal.firwin(),scipy.signal.lfilter()等函数。 - 使用
scipy.ndimage模块进行图像处理,如使用scipy.ndimage.imread(),scipy.ndimage.rotate(),scipy.ndimage.zoom(),scipy.ndimage.filters.gaussian_filter()等函数。
pandas
pandas是一个用于数据分析和处理的库,它提供了两种主要的数据结构:Series和DataFrame。Series是一维的带标签的数组,DataFrame是二维的带标签的表格。pandas的主要功能有:
- 创建和操作Series和DataFrame,如使用
pd.Series(),pd.DataFrame(),pd.read_csv(),pd.read_excel(),pd.to_csv(),pd.to_excel()等函数。 - 对Series和DataFrame进行索引和切片,如使用
a.loc[],a.iloc[],a.at[],a.iat[],a[],a[[ ]]等语法。 - 对Series和DataFrame进行数学运算,如使用
+,-,*,/,**,np.dot(),np.sin(),np.exp()等函数或运算符。 - 对Series和DataFrame进行统计分析,如使用
a.sum(),a.mean(),a.std(),a.min(),a.max(),a.idxmin(),a.idxmax(),a.describe()等函数。 - 对Series和DataFrame进行排序,如使用
a.sort_values(),a.sort_index()等函数。 - 对Series和DataFrame进行清理,转换,合并,重塑,分组,聚合等操作,如使用
a.dropna(),a.fillna(),a.apply(),a.map(),pd.concat(),pd.merge(),a.pivot(),a.stack(),a.unstack(),a.groupby(),a.agg()等函数。
matplotlib
matplotlib是一个用于绘制图形和可视化数据的库,它提供了一个类似于MATLAB的接口,以及一个面向对象的接口。matplotlib的主要功能有:
- 创建和操作图形对象,如使用
plt.figure(),plt.subplot(),plt.subplots(),plt.axes()等函数。 - 绘制各种类型的图形,如使用
plt.plot(),plt.scatter(),plt.bar(),plt.hist(),plt.pie(),plt.boxplot()等函数。 - 设置图形的样式和属性,如使用
plt.title(),plt.xlabel(),plt.ylabel(),plt.legend(),plt.grid(),plt.xlim(),plt.ylim(),plt.xticks(),plt.yticks(),plt.text(),plt.annotate()等函数。 - 保存和显示图形,如使用
plt.savefig(),plt.show()等函数。
二、解决一些具体问题的代码
numpy
计算两个矩阵的乘积
import numpy as np # 创建两个矩阵 a = np.array([[1,2,3],[4,5,6]]) b = np.array([[7,8],[9,10],[11,12]]) # 计算矩阵乘积 c = np.dot(a,b) # 打印结果 print(c)
输出:
[[ 58 64]
[139 154]]
scipy
求解一个非线性方程组
import scipy.optimize as opt # 定义方程组的函数 def f(x): return [x[0]**2 + x[1]**2 - 1, x[0] - x[1] + 0.5] # 用fsolve函数求解,给定初始值 x = opt.fsolve(f, [0,0]) # 打印结果 print(x)
输出:
[ 0.78867513 -0.21132487]
pandas
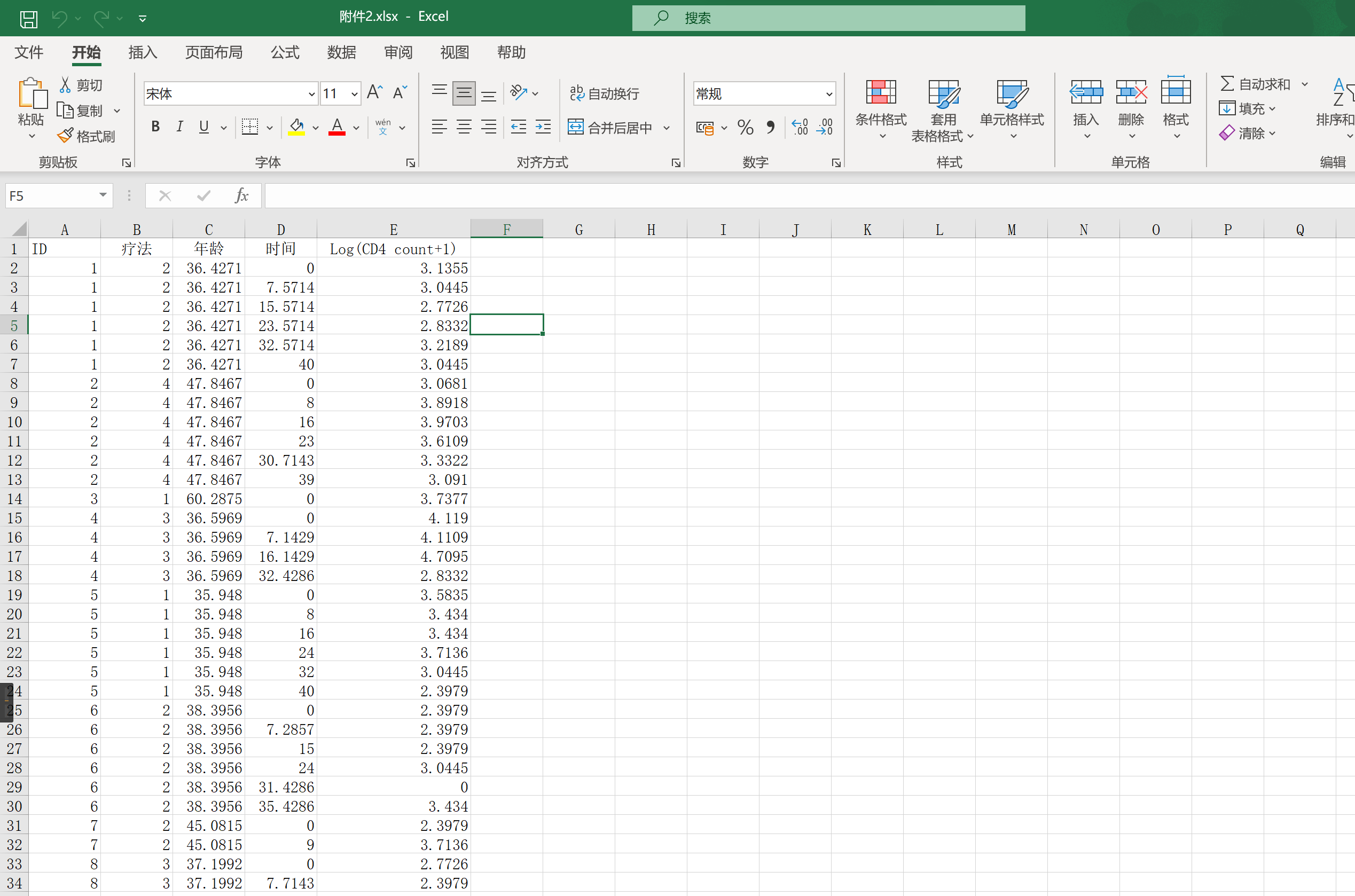
从一个txt文件中读取数据,输出到excel文件中
import pandas as pd # 读取txt文档中的内容 with open('B2006data/附件2.txt', 'r') as f: lines = f.readlines() # 跳过前面几行 skip_lines = 13 data = [] for line in lines[skip_lines:]: line = line.strip() # 使用split()函数将每一行的数据分割成多个元素 row = line.split() row_data = [] for element in row: try: # 尝试将元素转换为浮点数 row_data.append(float(element)) except ValueError: # 如果转换失败,将元素作为字符串存储 row_data.append(element) # 将每一行的数据储存在嵌套列表中 data.append(row_data) # 将数据写入Excel df = pd.DataFrame(data) df.to_excel('附件2.xlsx', index=False, header=False)
结果展示:
matplotlib
绘制阻尼曲线
import matplotlib.pyplot as plt import numpy as np plt.rcParams['font.family'] = 'SimHei' plt.rcParams['font.sans-serif'] = ['SimHei'] def draw(pcolor, nt_point, nt_text, nt_size): plt.plot(x, y, label='$exp_decay$', color=pcolor, linewidth=3, linestyle="-") plt.plot(x, z, "b--", label='$cos(x^2)$', linewidth=1) plt.xlabel('时间(s)') plt.ylabel('幅度(mv)') plt.title("阻尼衰减曲线绘制") plt.annotate('$\cos(2 \pi t) \exp(-t)$', xy=nt_point, xytext=nt_text, fontsize=nt_size, arrowprops=dict(arrowstyle='->', connectionstyle="arc3, rad=.1")) def shadow(a, b): ix = (x > a) & (x < b) plt.fill_between(x, y, 0, where=ix, facecolor='grey', alpha=0.25) plt.text(0.5 * (a + b), 0.2, r"$\int_a^b f(x) \mathrm{d}x$", horizontalalignment='center') def xy_axis(x_start, x_end, y_start, y_end): plt.xlim(x_start, x_end) plt.ylim(y_start, y_end) plt.xticks([np.pi/3, 2 * np.pi/3, 1 * np.pi, 4 * np.pi/3, 5 * np.pi/3], ['$\pi/3$', '$2\pi/3$', '$\pi$', '$4\pi/3$', '$5\pi/3$']) x = np.linspace(0.0, 6.0, 100) y = np.cos(2 * np.pi * x) * np.exp(-x) + 0.8 z = 0.5 * np.cos(x ** 2) + 0.8 note_point, note_text, note_size = (1, np.cos(2*np.pi)*np.exp(-1)+0.8), (1, 1.4), 14 fig = plt.figure(figsize=(8, 6), facecolor="white") plt.subplot(111) draw("red", note_point, note_text, note_size) xy_axis(0, 5, 0, 1.8) shadow(0.8, 3) plt.legend() plt.show()



