leetcode69 X的平方根的几种解法
第一种自然就是调APi啦(手动滑稽)
public int mySqrt(int x) { return (int)Math.sqrt(x); }
时间是52 ms,还超过了1/5的人呢
第二种 二分法
就是在0--X之间一半地一半地砍,最后直到左右边界的中间的数 = X/mid,这样做是防止因为mid数字太大而导致溢出
看代码吧,跟排序类似
public int getSqrtByDevide(int x) { if (x<=1) { return x; } int low = 0; int high = x; int mid = 0; while(low<=high) { mid = low + (high - low)/2; if(mid == (x/mid)) return mid; else if(mid < (x/mid)) low = mid + 1; else high = high -1; } return high; }
这种比上种稍微快一点:45 ms
第三种 牛顿迭代法
刚开始还没搞懂是怎么回事,后来看了网上的一些帖子才明白.
首先拿此题来说,假设最后的输出的结果x² = N,(N是函数参数终点x),这里可以看成一个函数,即f(x) = x² - N;
那么最终的目的就变成了求这个函数的零点了
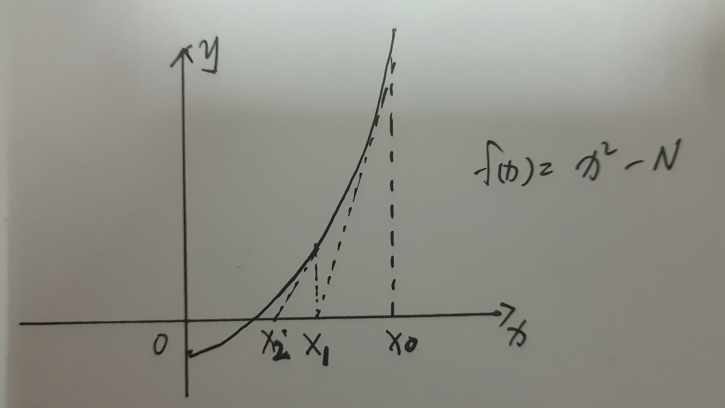
迭代过程就是从X0开始,看它的平方是不是等于N,是就返回,不是就在X0对应的在函数图像上的点上做切线
再求这个切线和x轴的交点,重复上面的步骤:
f(x) = x² - N 设点Xi,则经过点(Xi,f(Xi))处的切线方程为g(x) = f(Xi)+ f'(Xi)(x - Xi) 令g(x) = 0 得x = Xi - f(Xi)/f'(Xi) 又f(Xi) = Xi² - N 代入得最终迭代式子: x = (Xi + N/Xi)/2;
然后代码:
public int getSqrtByNewton(int x) { if (x<=1) { return x; } double last = -1;//最后 double ans = 1;//结果 while(last!=ans) { last = ans;//将迭代前的ans存起来,如果和迭代后ans相等,代表非常逼近 ans = (ans+x/ans)/2; } return (int)ans; }
这个还是很快的:27ms
第四种 "0x5f3759df"算法
这个的原理我也没搞太清楚,好像有个专门的论文将这个算法的,很神奇,经常用于图形学游戏领域一些场景里面
那我就只贴个代码吧(凑个字数...)
public int mySqrt(int x) { long t = x; t = 0x5f3759df - (t >> 1); while (!(t*t <= x && (t+1)*(t+1) > x)) t = (x/t + t)/2; return (int)t; }
这里有讲,挺麻烦的,我就知道打一波666吧...
http://www.sandaoge.com/info/new_id/30.html?author=1


