20172314 2018-2019-1《程序设计与数据结构》第八周学习总结
教材学习内容总结
堆
-
堆:是一颗完全二叉树,每一个结点都小于等于左右孩子(最小堆),或大于等于左右孩子(最大堆)他的每一个子树也是最小堆或最大堆。
-
堆的操作
-
addElement操作(堆的插入)
- 插入新结点时,是作为叶子结点插入的,且一定要保持树的完整性。如果最下层不满,插入到左边的下一个空位,如果最底层是满的,插入到新一层的左边第一个位置。
- 如果插入的数相对树而言较小,则需要在插入后进行重排序

-
removeMin方法(堆的删除)
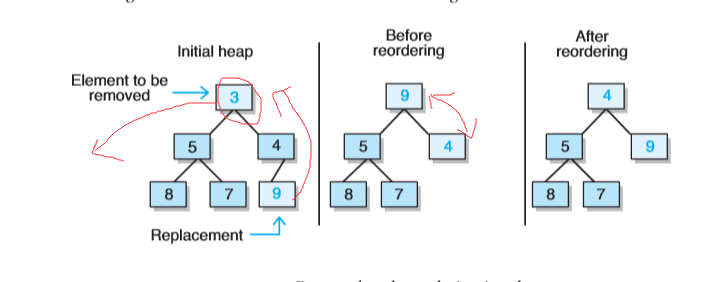
- 由于最小元素储存在根处,为了维持树的完整性,那么只有一个能替换根的合法元素,且它是存储在树中最末一片叶子上的元素(将是树中h层上最右边的叶子)。
- 将替换元素移到根部后,必须对该堆进行重排序。
-
findMin操作
- 这个方法需要返回在最小堆中最小元素的引用,由于最小堆中最小元素在根处,所以只需返回根部元素即可。
使用堆:优先级队列
- 具有更高优先级的项目在先。
- 具有相同优先级的项目使用先进先出的方法来确定其排序。
- 虽然最小堆不是一个队列,但它提供了一个高效的优先级队列实现。
用链表实现堆
- 由于要求插入元素后能够向上遍历树,所以堆结点中必须存储指向双亲的指针。
- 由于BinaryTreeNode类没有双亲指针,所以要创建一个HeapNode类开始链表实现。
- addElement操作
- 在适当位置添加一个新元素
- 对堆进行重排序以维持其排序属性
- 将lastNode指针重新设定为指向新的最末结点
- 在这个方法中用到了getNextParentAdd方法(返回指向某结点的引用,该结点为插入结点的双亲),还有一个heapifyAdd方法,(完成对堆的任何重排序,从新叶子开始向上处理至根处)
- addElement操作有三步
- 首先要确定插入结点的双亲(从堆的右下结点往上遍历到根,再往下遍历到左下结点,时间复杂度为2*logn)
- 其次是插入新结点(只涉及简单的赋值语句,时间复杂度为O(1))
- 最后是从被插入叶子处到根处的路径重排序,来保证堆的性质不被破坏(路径长度为logn,最多需要logn次比较)
- 因此addElement操作的复杂度为2*logn+1+logn,即为O(logn)
- removeMin操作
- 用最末结点处的元素替换根处元素
- 对堆进行重排序
- 返回初始的根元素
- addElement操作
用数组实现堆
- 数组相比于链表,优点是不需要遍历来查找最末一片叶子或下一个插入结点的双亲,直接查看数组的最末一个元素即可。
- 在数组中,树根存放在0处,对于每一个结点n,n的左孩子位于数组2n+1处,n的右孩子位于数组的2(n+1)处。同样,反过来查找时,对于任何除了根之外的结点,n的双亲位于(n-1)/2位置处。
- addElement操作
- 在恰当位置处添加新结点
- 对堆进行重排序以维持其属性
- 将count递增1
- 只需要一个heapifyAdd方法进行重排序,不需要重新确定新结点双亲位置。此方法的时间复杂度是O(logn)
- removeMin操作
- 用最末元素替换根元素
- 对堆进行重排序
- 返回初始根元素
- 由于末结点存储在数组的count-1位置处,所以不需要确定最新末结点的方法,此方法复杂度为O(logn)
- findMin操作
仅仅返回根处元素即可,就是数组的位置0处,复杂度为O(1)
使用堆:堆排序
- 堆排序的过程(由两部分构成,添加和删除)
- 将列表的每一元素添加到堆中
- 一次一个将他们从根删除,再次存放到数组中
- 最小堆时得到的排序结果是升序,最大堆时得到的排序结果是降序
- 对于每一个结点来说,添加和删除操作的复杂度都是O(logn),所以对于有n个结点的堆来说,复杂度是O(nlogn)
- 堆排序的复杂度具体分析
- 堆化过程一般是用父节点和他的孩子节点进行比较,取最大的孩子节点和其进行交换;但是要注意这应该是个逆序的,先排序好子树的顺序,然后再一步步往上,到排序根节点上。然后又相反(因为根节点也可能是很小的)的,从根节点往子树上排序。最后才能把所有元素排序好。对于每个非叶子的结点,最多进行两次比较操作(与两个孩子)因此复杂度为2*n
- 排序过程就是把根元素从堆中删除,删除每个元素复杂度为logn,对所有元素来说,复杂度为nlogn。
- 所以是2*n + nlogn,复杂度是O(nlogn)

教材学习中的问题和解决过程
-
问题一:getNextParentAdd方法的代码理解
-
问题一解决:
* 第一种情况
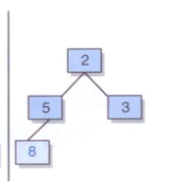
首先考虑while循环,result为8,他是左孩子,所以不进入while循环,接着往下,他不是根结点,他不是父结点的右孩子,所以result为父结点5,即返回的插入结点的双亲。
* 第二种情况
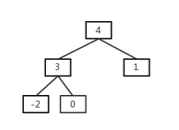
result为0,双亲结点的左孩子为-2,所以进入while循环,result为3,接下来进入if语句,他不是根结点,而且父结点的右孩子(1)不为空,所以返回的插入结点的双亲结点是1
* 第三种情况
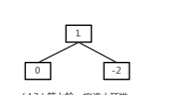
while循环中,result(2)不是左孩子,所以result为双亲结点1,往下,他是根结点,而且左子树不为空,result为左孩子0.这种情况就相当于满树时插入到新一层的左边位置。private HeapNode<T> getNextParentAdd() { HeapNode<T> result = lastNode;// 当前的空白结点 while ((result != root) && (result.getParent().getLeft() != result))//如果当前不是一个满堆,他不是左孩子 result = result.getParent(); if (result != root) { // /不是一个满堆 if (result.getParent().getRight() == null)//右边是空位 result = result.getParent(); else {//右边不空 result = (HeapNode<T>) result.getParent().getRight(); // 不断的向下寻找最后的父结点 while (result.getLeft() != null) result = (HeapNode<T>) result.getLeft(); } } else {// 当前堆是一个满堆 while (result.getLeft() != null) result = (HeapNode<T>) result.getLeft(); } return result; } -
问题二:heapifyAdd方法的代码理解
-
问题二解决:举个例子,
private void heapifyAdd() { T temp; HeapNode<T> next = lastNode; temp = next.getElement(); while ((next != root) && (((Comparable) temp) .compareTo(next.getParent().getElement()) < 0)) { next.setElement(next.getParent().getElement()); next = next.parent; } next.setElement(temp); }
如图在树中插入结点2,那么next指向2,temp=2,这时next不是根结点,并且2(temp)比4(next.getParent().getElement())小,所以现在next的值设置为4(即原来2的那个位置变成4),next指向原来next的父亲结点(即原来的4位置),然后将next的值设为temp即2(原来4的位置变为2),这样就将2和4换位,实现了重排序。 -
问题三:堆排序的过程
-
问题三解决:首先把待排序的元素在二叉树位置上排列,然后调整为大顶堆或小顶堆,接下来进行排序,以小顶堆为例,根结点为最小,所以拿掉根,然后对堆进行调整,使其符合小顶堆的要求,然后新的堆顶又是最小的,将其拿掉,如此循环...蓝墨云关于这个的测试题,重新梳理一下如图,大顶堆的过程与其类似,但注意在代码实现中,小顶堆排序结果为升序,大顶堆排序结果为降序
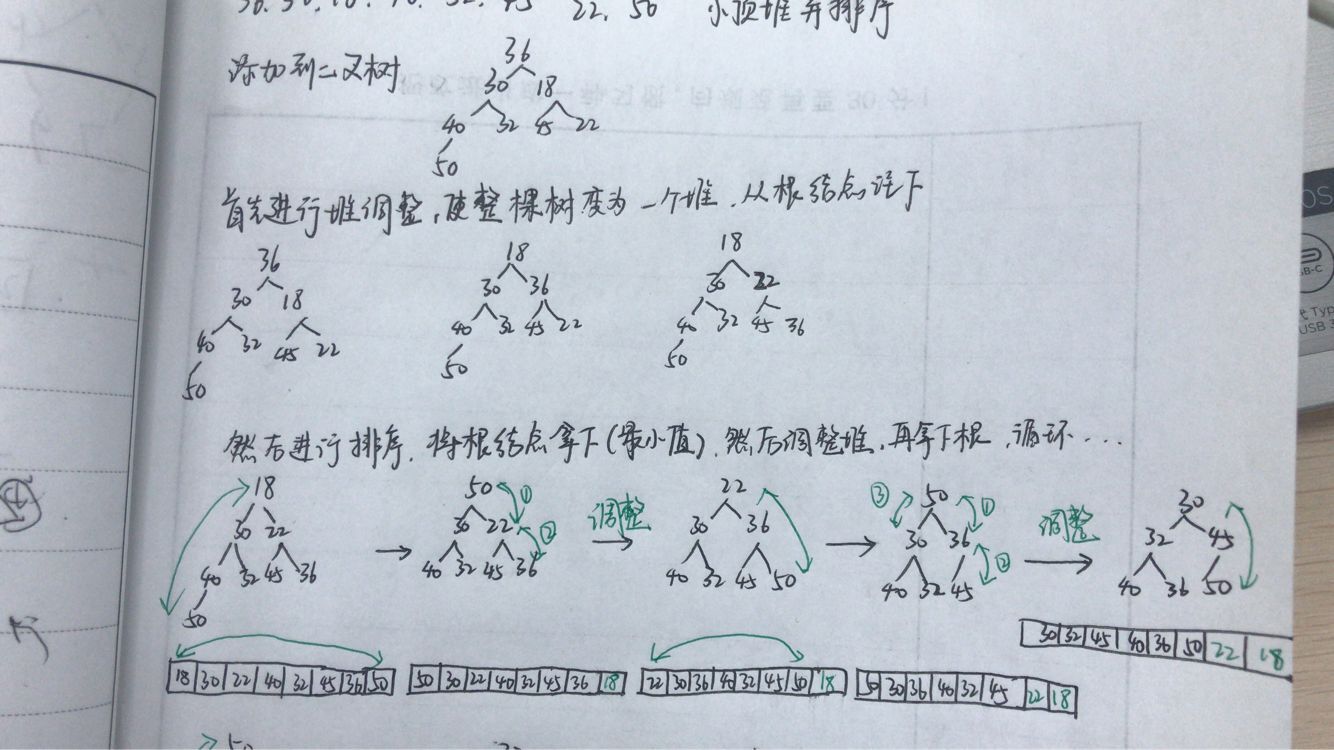
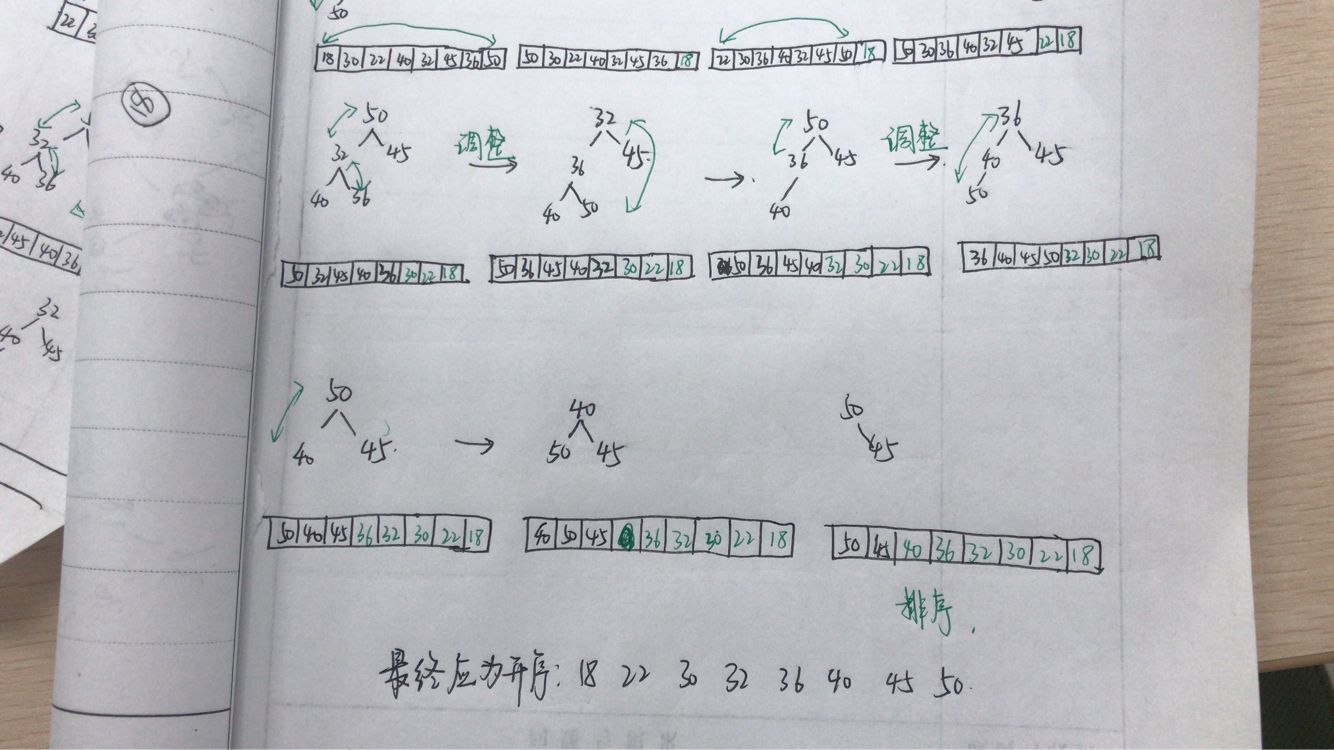
-
问题四:对于优先级队列的理解
-
问题四解决:队列是一种特征为FIFO的数据结构,每次从队列中取出的是最早加入队列中的元素。但是,许多应用需要另一种队列,每次从队列中取出的应是具有最高优先权的元素,这种队列就是优先级队列。优先级队列的特点:
- 优先级队列是0个或多个元素的集合,每个元素都有一个优先权或值。
- 当给每个元素分配一个数字来标记其优先级时,可设较小的数字具有较高的优先级,这样更方便地在一个集合中访问优先级最高的元素,并对其进行查找和删除操作。
- 在最小优先级队列(min Priority Queue)中,查找操作用来搜索优先级最小的元素,删除操作用来删除该元素。在最大优先级队列(max Priority Queue)中,查找操作用来搜索优先级最大的元素,删除操作用来删除该元素。
- 每个元素的优先级根据问题的要求而定。当从优先级队列中删除一个元素时,可能出现多个元素具有相同的优先权。在这种情况下,把这些具有相同优先权的元素按先进先出处理。
代码调试中的问题和解决过程
-
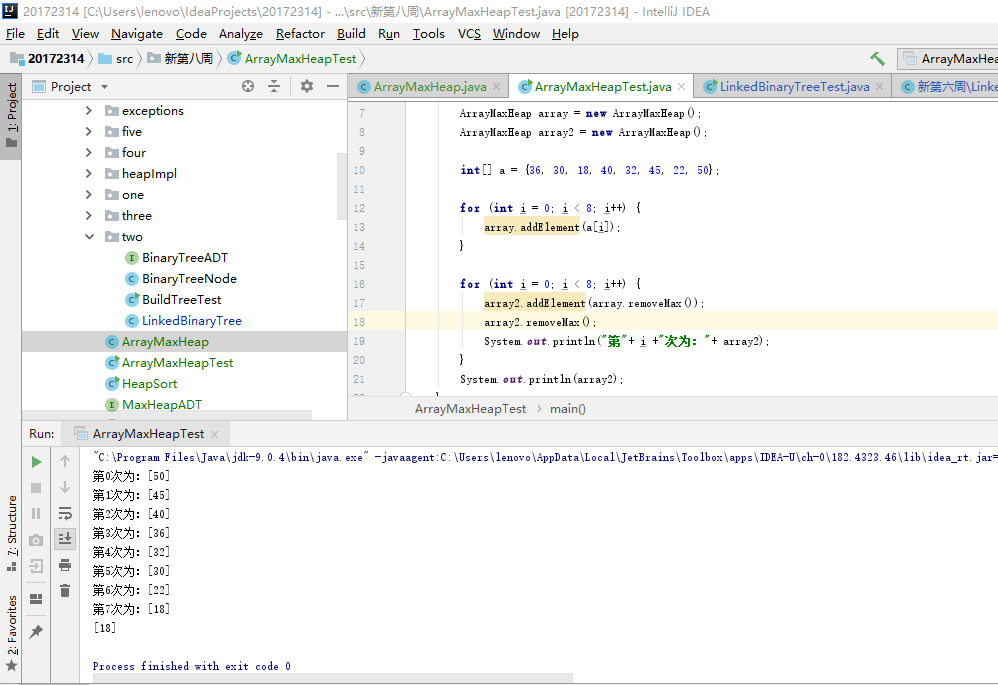
问题一:在做蓝墨云测试构造大顶堆并排序时,对于过程的输出结果是每次将最大数从堆顶拿下时的结果,并不是显示每次排序时的数组情况。
-
问题一解决:主要错误之处在于测试类,如图中显示,我的过程记录是
for(int i=0;i<8;i++){ array2.addElement(array.removeMax); array2.removeMax(); System.out.println("第"+i+"次为:"+ array2); }首先,在循环中array中每次拿掉的最大数添加到array2中,然后输出的是array2中的最大数,那么就相当于每次把array中的最大数输出,array2没有什么作用。应该为
for (int i = 0; i <a.length; i++) { array2[i]=array.removeMax(); System.out.println("第"+ i +"次为:"+ array); }这样就把array2的作用发挥出来了,array2中存放array中依次弹出的最大数,在array2中降序排列,然后每次输出array数组,显示现在数组情况,排序的结果就可以用类似上面的for循环依次将array2中的数输出。
-
问题二:在做PP12.1时,对于优先级队列的输出情况理解有问题。
-
问题二解决:测试类通过在循环中使用
queue.removeNext()方法,是由于PriorityQueue类中removeNext方法继承了ArrayHeap类中的removeMin方法,而在ArrayHeap类中,removeMin又使用了方法heapModifyRemove,其中else if (((Comparable)tree[left]).compareTo(tree[right]) < 0) next = left当left比right小时,返回左,我最开始不理解的是在优先级队列中,当优先级相同时
if (arrivalOrder >obj.getArrivalOrder())//优先级相同时,先进先出 result = 1;应返回左边的arrivalOrder,但在heapModifyRemove中来说,却返回compareTo右边的,所以我觉得矛盾,进行多次测试后我发现输出的结果没有错。又仔细看代码之后发现,优先级相同时,返回1的情况是arrivalOrder较大,那么就代表它是后进的,并不是跟优先级一样大的先,arrivalOrder越大代表晚进,应该后出,所以正好反一下。
-
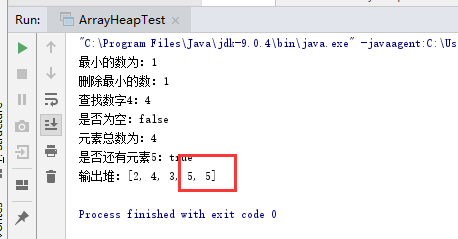
问题三:实现ArrayHeap类时,发现输出结果总是多一个数
-
问题三解决:参考了谭鑫同学的博客,里面提到了解决办法,如图
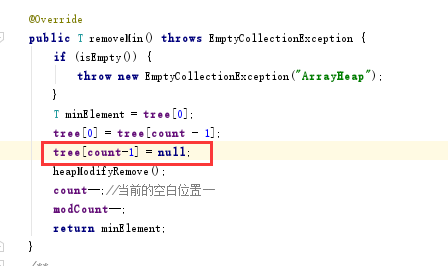
添加语句之后解决问题,原因是在将根结点拿掉并用末叶子结点替换后并没有将叶结点删除,所以导致出现两次,添加语句tree[count-1] = null;之后,将其值设置为空,相当于删除。
代码托管
上周考试错题总结
-
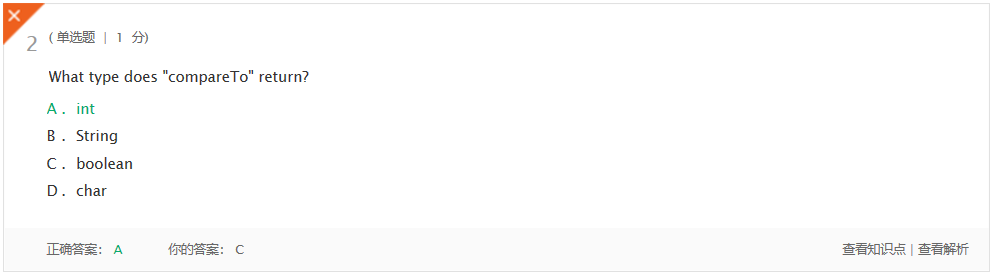
错题一:
-
错题一解决:CompareTo方法返回值是int型的,如果前者比后者大的话返回1,小的话返回-1,相等返回0.
结对及互评
- 20172305谭鑫:谭鑫的博客中提到的”问题1:实现优先级队列的二叉堆、d堆、左式堆、斜堆、二项堆都是什么意思?和最小堆、最大堆有什么区别?”是我没有学习过的,学习到了左式堆,二项堆,斜堆等堆。同时参考他的博客解决了一个代码问题,非常有价值。
- 20172323王禹涵:王禹涵的博客对代码的解释很详尽,排版精美,很舒适。
其他
这一章感觉原理很容易理解,逻辑简单,但用代码实现不好理解,但是书上代码的可用性很高,然后实验方面也花费较长时间,总结出来就是要尽早去掌握核心代码再开展学习。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | |
|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 |
| 第一周 | 0/0 | 1/1 | 8/8 |
| 第二周 | 1163/1163 | 1/2 | 15/23 |
| 第三周 | 774/1937 | 1/3 | 12/50 |
| 第四周 | 3596/5569 | 2/5 | 12/62 |
| 第五周 | 3329/8898 | 2/7 | 12/74 |
| 第六周 | 4541/13439 | 3/10 | 12/86 |
| 第七周 | 1740/15179 | 1/11 | 12/97 |
| 第八周 | 5947/21126 | 1/12 | 12/109 |


