数据结构与算法分析_二阶指针做为形参_链表头插入法工作流程及测试_链表尾插入法工作流程及测试_双向链表_优先队列(堆)测试_优先队列上滤插入和下滤删除_C语言实现最小堆和堆排序_队列(循环队列方法实现)_栈_快速排序_冒泡排序_生成n位格雷码

目录

1、二阶指针做为形参的目的(使实参的值发生改变)

2、链表头插入法工作流程及测试

3、链表尾插入法工作流程及测试

    3.1调试deleteElementByIndex()函数发现，主函数中的linkPtr经过showlinkList()函数之后已经成为了NULL空指针

    3.2改进

    3.3链表翻转(20200321)

    3.4合并两个有序的链表

　3.5k个为一组反转链表

4、双向链表

    (1) 链表初始化和创建

    (2) 在链表的第i个位置插入数据data

    (3) 删除链表中的第i个节点

    (4) 删除所有元素

    (5) 最后的修改

5、优先队列(堆)测试

     5.1++i和i++运算符的测试        m41

     5.2优先队列上滤插入和下滤删除

     5.3 C语言实现最小堆和堆排序

6、队列(循环队列方法实现)

    (1) 队列结构体定义;

    (2) 循环队列出队入队图解

    (3) 临界状态下，front和rear的取值方式

    (4) 总结

    (5) 循环队列中存储的元素个数计算方式

    (6)调试

    (7)C++中的queue类

7、栈

    (1)自己实现

    (2)使用C++库函数stack

    (3)使用两个站实现一个队列：参考笔试练习：m12

8、快速排序  时间复杂度O(nlogn)

    (1)实现方法一

    (2)实现方法二

    (3)使用快速排序算法找到数组中的k大的值

    (4)快速排序是一种不稳定的排序方法的原因

9、冒泡排序   时间复杂度O(n^2)

10、生成n位格雷码

11、二叉树

    1、基本概念以及初级实现和遍历方法

    2、非递归方法实现三种遍历
　　  (1)非递归方式前序遍历---使用栈数组
　  　(2)非递归方式中序遍历---使用栈数组
　  　(3)非递归方式后序遍历---使用栈数组

　  　(4)层序遍历---使用队列

    3、二叉树中的平衡的概念(顺便引出平衡二叉树的概念)    判断二叉树是否为平衡二叉树链接

12、C++中的四个智能指针:auto_ptr,shared_ptr,weak_ptr,unique_ptr，其中auto_ptr已经被C++11抛弃

       1、auto_ptr(C++98中的放案,C++11已经抛弃)

　　2、unique_ptr

　　3、shared_ptr    自己手写的shared_ptr的C++实现

　　4、weak_ptr

　　5、总结

　　6、测试两个普通指针是否可以指向同一块内存区域

　　7、VS2017环境下内存泄漏检测

　　8、make_shared

13、友元函数复习

    1、以前学习的友元类传送门

    2、复习

14、虚函数复习

    1、虚函数和普通函数的区别

    2、抽象基类(使用纯虚函数)

    3、虚基类传送门

    4、函数指针定义方法

    5、虚函数表的进一步解释

15、堆排序(重新学习)  时间复杂度O(nlogn)，这里的堆实现方法为实现一颗完全二叉树

    1、一个一个的插入实现方法

    2、删除堆顶元素，即删除堆中最小元素

    3、总结

16、二分法

    1、二分法查找简答实现

    2、实例：求f(x) = x ^ 3 - x - 1在[1，1.5]内的一个实根，使误差不超过0.005。 

    3、远亲不如紧邻笔试题---使用二分法实现

        1)自己先写的(有缺陷，在二分法子函数那里)
        2)看来答案之后的修改版本
        3)二分法总结

    4、移位与乘除法的关系

17、使用stringstream类将string类型转换为int、float、double等类型

18、归并排序原理和C++实现  时间复杂度O(nlogn)，适用于元素较多的时候排序

19、插入排序  时间复杂度为O(n^2)    希尔排序(shell排序)

20、单调栈

　　(1)单调栈的应用---逛街

21、以前写的博客---无缺陷的String类实现方法----关于复制构造函数和赋值构造函数

1、二阶指针作为形参的目的

1)普通变量做为形参，不能改变主函数中实参的值

例子：

//01)形参改变，实参并没有改变的例子
#include <iostream>

using std::cout;
using std::endl;

/*交换a和b的值子函数*/
void changeParameters(int a, int b)
{
    int temp;
    temp = a;
    a = b;
    b = temp;
}

int main()
{
    int num1 = 12;
    int num2 = 22;
    cout << num1 << " , " << num2 << endl;
    changeParameters(num1, num2);  //此时num1和num2知识形参交换,实际参数并没有交换
    cout << num1 << " , " << num2 << endl;

    system("pause");
    return 0;
}

运行结果：

2)一阶指针作为形参，变量地址作为实参可以改变主函数中实参的值

例子：

//02)实参发生改变的例子
#include <iostream>

using std::cout;
using std::endl;

/*交换a和b的值子函数*/
void changeParameters(int* a, int* b)
{
    int temp;     //此处改成int* temp交换地址，然后把*a和*b去掉也是可以的
    temp = *a;
    *a = *b;
    *b = temp;
}

int main()
{
    int num1 = 12;
    int num2 = 22;
    cout << num1 << " , " << num2 << endl;
    changeParameters(&num1, &num2);  //此时是对存储空间这的两个数进行交换,所以num1和num2的值会发生交换
    cout << num1 << " , " << num2 << endl;

    system("pause");
    return 0;
}

运行结果：

3)二阶指针做为形参,对指针用取地址运算符取地址后作为实参，可以改变实参的值

例子：

#include <iostream>

using std::cout;
using std::endl;

/*交换a和b的值子函数(相关解释见下)*/
void changeParameters(int** a, int** b)
{
    int* temp;
    temp = *a;    //保存*a指向的地址
    *a = *b;      //将*b指向的地址赋给*a指向的地址
    *b = temp;    
}

int main()
{
    int a = 12;
    int b = 22;
    int* num1 = &a;
    int* num2 = &b;
    cout << *num1 << " , " << *num2 << endl;
    changeParameters(&num1, &num2);  //对指针取地址,即只想指针的指针，或者是地址的地址
    cout << *num1 << " , " << *num2 << endl;

    system("pause");
    return 0;
}

/*
int a = 12;  //假设存储a变量的地址是00424A30
int* pc = &a;  //则pc指向地址00424A30，假设存储pc的地址是00424A38
int** ppc = &pc;  //ppc指向pc的地址(00424A38)

cout << "a的地址是: " << &a << endl;  //打印  a的地址是: 00424A30
cout << "pc的值是: " << pc << endl;  //打印   pc的值是: 00424A30  pc的值就是a的地址
cout << "*pc的值是: " << pc << endl;  //打印  *pc的值是: 12 
cout << "pc的地址是: " << &pc << endl;  //打印  *pc的值是: 00424A38
cout << "ppc的值是: " << ppc << endl;  //打印  ppc的值是: 00424A38  （ppc的值就是pc的地址）
cout << "*ppc的值是: " << ppc << endl;  //打印  ppc的值是: 00424A38  （ppc的值就是pc的地址）
cout << "*(*ppc)的值是: " << *(*ppc) << endl;  //打印  ppc的值是: 2  
*/

运行结果：

在例子中的一个解析：

int a = 12;  //假设存储a变量的地址是00424A30
int* pc = &a;  //则pc指向地址00424A30，假设存储pc的地址是00424A38
int** ppc = &pc;  //ppc指向pc的地址(00424A38)

cout << "a的地址是: " << &a << endl;  //打印  a的地址是: 00424A30
cout << "pc的值是: " << pc << endl;  //打印   pc的值是: 00424A30  pc的值就是a的地址
cout << "*pc的值是: " << pc << endl;  //打印  *pc的值是: 12 

cout << "pc的地址是: " << &pc << endl;  //打印  *pc的值是: 00424A38
cout << "ppc的值是: " << ppc << endl;  //打印  ppc的值是: 00424A38  （ppc的值就是pc的地址）

cout << "*ppc的值是: " << ppc << endl;  //打印  ppc的值是: 00424A38  （ppc的值就是pc的地址）
cout << "*(*ppc)的值是: " << *(*ppc) << endl;  //打印  ppc的值是: 2  

参考博客：https://blog.csdn.net/qq_34991245/article/details/81868212

04)二阶指针作为形参，一阶指针的地址作为实参，将形参赋给子函数中的一个变量,后改变该变量的值不会影响实参的值

例子：

#include <iostream>

using std::cout;
using std::endl;

/*交换a和b的值子函数(相关解释见下)*/
void changeParameters(int** a, int** b)
{
    int* temp = *a;
    int p = 33;
    temp = &p;  //验证一下实参a的值会不会改变,此句不会改变实参a的值
    *temp = p;  //此句不会改变实参a的值
}

int main()
{
    int a = 12;
    int b = 22;
    int* num1 = &a;
    int* num2 = &b;
    cout << *num1 << " , " << *num2 << endl;
    changeParameters(&num1, &num2);  //对指针取地址,即只想指针的指针，或者是地址的地址
    cout << *num1 << " , " << *num2 << endl;

    system("pause");
    return 0;
}

运行结果：

05)二阶指针作为形参，一阶指针的地址作为实参，改变子涵数(形参)实参的值会影响实参的值

#include <iostream>

using std::cout;
using std::endl;

/*交换a和b的值子函数(相关解释见下)*/
void changeParameters(int** a, int** b)
{
    int p = 33;
    *a = &p;  //直接对形参(实参)赋值这样是会改变实参的值的
}

int main()
{
    int a = 12;
    int b = 22;
    int* num1 = &a;
    int* num2 = &b;
    cout << *num1 << " , " << *num2 << endl;
    changeParameters(&num1, &num2);  //对指针取地址,即只想指针的指针，或者是地址的地址
    cout << *num1 << " , " << *num2 << endl;

    system("pause");
    return 0;
}

运行结果：

06)一阶指针做为实参和形参

(1)一阶指针做为实参和形参以下实现方法不会改变实参的值

这是由于指针传参也会给指针复制一份，并将这个复制的指针传递给子涵数，然后将这个复制得到的指针重新指向了一个新的地址，但是原指针还是指向原来的地址

void func(int* p) {
    int m_value = 1;
    p = &m_value;
}

如下：

#include <iostream>

using std::cout;
using std::endl;


void func(int* p) {
    int m_value = 1;
    p = &m_value;
    //*p = m_value;
}

int main()
{
    int num1 = 12;
    int num2 = 22;

    int *pn = &num1;
    cout << "*pn=" << *pn << endl;
    func(pn);
    //func(&num1);  //也是一样的
    cout << "*pn=" << *pn << endl;

    system("pause");
    return 0;
}

执行结果：

结果没有发生改变的原因：

假如主函数中pn指向的内存块标记为a，那么当调用func(pn)的时候，形参p和实参pn都指向了内存块a，而上面的子函数func()只是把形参p的指向改变了，主函数中的pn的指向还是不变的。

(2)下面的方法将会改变实参的值

void func(int* p) {
    int m_value = 1;
    *p = m_value;
}

如下：

#include <iostream>

using std::cout;
using std::endl;


void func(int* p) {
    int m_value = 1;
    *p = m_value;
}

int main()
{
    int num1 = 12;
    int num2 = 22;

    int *pn = &num1;
    cout << "*pn=" << *pn << endl;
    func(pn);
    //func(&num1);  //也是一样的
    cout << "*pn=" << *pn << endl;

    system("pause");
    return 0;
}

执行结果：

此时可以改变主函数中pn指向的内存的值，这是由于形参p和实参pn都指向了一块内存，而上面的子函数通过形参p将这块内存中的值改变了，所以主函数中实参pn指向的值也会发生了改变。

 

2、链表头插入法工作流程及测试

01)头插法工作流程：

/*链表*/

#include <iostream>

using std::cin;
using std::cout;
using std::endl;

typedef int ElementType;

/*定义一个结构*/
struct linkList
{
    ElementType Element;  //定义结构中的一个数据(数据域)
    linkList* next;  //定义指向下一个结构的指针(指针域)
};

typedef struct linkList *PtrtoNode;  //PtrtoNode是一个类型,可以定义变量,且PtrtoNode是一个指针,指向结构体Node
typedef PtrtoNode List;  //为PtrtoNode起别名为List
typedef PtrtoNode Position;  //为PtrtoNode起别名为Position

void initlinkList(linkList** head);
void destroylinkListByHead(linkList** head);
void destroylinkListByTail(linkList** head);
void insertDatabyHead(linkList** head);
void insertDatabyTail(linkList* head);
void showlinkList(linkList** head);
linkList* indexof(linkList* head, int index);
int deleteElementByIndex(linkList* head, int index);

#include "stacktp1.h"

/*
01)链表的初始化(给头节点申请空间),所以在使用改函数的时候,只传入已创建结构的next指针即可;
02)使用指向指针的指针作为形参的原因在于要传入的参数是一个指针(要传入的参数是结构中的next指针),
   如果形参定义为一层指针,那么就会发生形参改变而实参并没有发生任何改变的情况。
*/
void initlinkList(linkList** head)
{
    if ((*head) == NULL)  //如果结构这的next指针为空，那么表明已经初始化完成;刚刚这里写成了 != 导致在插入数据的时候head->next访问不了
        return;
    *head = (linkList*)malloc(sizeof(linkList));  //给结构分配足够的内存空间
    (*head)->Element = 0;
    (*head)->next = NULL;  //head此时即是头节点也是尾节点，因为此时head指向了NULL
}

/*
01)链表的销毁
02)链表所有节点包括头结点都是动态申请的堆空间，使用完毕后必须手动释放，这里的销毁要把所有的节点空间全部释放;
03)方法一：从链表头开始遍历，也就是从前向后逐个释放每一个节点的空间
*/
void destroylinkListByHead(linkList** head)
{
    linkList* header = *head;
    linkList* p;
    while ( header != NULL)  //原来这里的条件是(*head)!=NULL，导致p->next指向了空指针;或者是循环了无数次
    {
        p = header;         //讲当前数据节点保存下来
        header = p->next;   //将下一个数据节点保存下来
        free(p);           //讲当前节点空间释放
    }
    free(header);  //释放头节点
    head = NULL;  //空间释放完的指针指向空指针
}

/*
01)方法二:从链表尾部向头部开始销毁，就不用临时保存
02)用递归遍历到最后一个结点，逐层向上返回，销毁每一个节点，顺序就是从头尾向头结点的顺序销毁。
*/
void destroylinkListByTail(linkList** head)
{
    if ((*head) == NULL)
        return;
    destroylinkListByTail(&((*head)->next));  //递归调用
    free(*head);
    head = NULL;
}

/*
01)向链表这插入数据
02)头插法：每次在头结点H的后面插入一个输入的数据，链表中的数据顺序和实际输入顺序相反
03)插入的过程主要是：先申请一个新的结点，链表不像数组一次性分配指定长度的空间，
   链表是需要增长一个就再申请一份，然后链接起来。申请完了之后给节点赋值，让新申请的节
   点指向头结点的next，也就是node->next = h->next，再让头结点指向这个新节点，
   H->next = node就完成插入操作。
04)传入的参数可以是头结点(头节点指向的是NULL)
05)传入的参数也可以是一个linkList结构的地址
06)以为此时是要向一个链表中插入数据，所以在使用malloc之后并没有释放内存
*/
void insertDatabyHead(linkList** head)
{
    linkList* node;  //新建一个需要插入的节点
    int x;
    cout << "请输入数据(-1结束)：" << endl;
    cin >> x;
    while (x != -1)
    {
        node = (linkList*) malloc(sizeof(linkList));    //为需要插入的节点分配空间    
        node->Element = x;
        //如果头节点指向的是NULL,所以下面这一句node->next换成NULL也可以
        node->next = (*head)->next; //使node成为head指向的一个节点之后的节点
        (*head)->next = node;  //使
        cout << "请输入数据(-1结束)：" << endl;  //接着输入数据
        cin >> x;
    }
}

/*
01)向链表这插入数据
02)尾插法：每次插入新的数据在链表的尾部插入就行，链表中的数据顺序和实际输入顺序相同
03)先找到链表的尾节点H->next == NULL，就是最后一个节点，同样插入就行。相比头插法，
   尾插法插入数据的时候如果链表不是一条空链表，得遍历先找到尾节点。
04)传入的参数的头结点(头节点指向的是NULL)
05)输入的参数是一个linkList结构的地址
*/

void insertDatabyTail(linkList* head)
{
    linkList* node;
    linkList* remove;
    int x;
    while (head->next != NULL)  //如果head不是尾节点,那么找到尾节点,并使head成为尾节点；尾节点指向NULL
        head = head->next;
    remove = head;  //将head(尾节点)赋给remove,是remove也成为尾节点
    cout << "请输入要插入的数据(-1结束): " << endl;
    cin >> x;
    while (x != -1)
    {
        node = (linkList*)malloc(sizeof(linkList));
        node->Element = x;
        node->next = remove->next;  //此处也可以使用head->next，但使用remove是为了循环大计
        remove->next = node;  //此处也可以使用head->next，但是链表就是断的了
        remove = node;  //为下一次循环做准备
        cout << "请输入要插入的数据(-1结束): " << endl;
        cin >> x;
    }
}

/*
01)打印链表
02)输入为当前节点，或者是一个结构的地址
*/

void showlinkList(linkList** head)
{
    if ((*head)->next == NULL )  //如果当前节点是头节点，则指向下一个节点;以为头节点是没有数据的
        (*head) = (*head)->next;
    (*head) = (*head)->next;  //不显示头结点中的元素;上面那个if肯定不会被执行的,因为传入的参数是头结点,头结点的下一个节点肯定不是空(只要有数据)
    while ((*head) != NULL  )
    {
        cout << (*head)->Element << endl;
        (*head) = (*head)->next;
    }
}

/*
01)删除第index个节点
*/
/*返回第index个节点*/
linkList* indexof(linkList* head, int index)
{
    linkList* p;
    if (head->next == NULL)
    {
        cout << "输入的当前节点为头节点" << endl;
        return NULL;
    }
    int j;
    for (j = 1, p = head->next; p != NULL && j < index; j++)  //如果index等于1,则该for循环会忽略p=NULL的情况
        p = p->next;
    return j == index ? p : NULL;
}
/*删除第index个节点*/
int deleteElementByIndex(linkList* head, int index)
{
    linkList* p;
    linkList* temp;
    p = indexof(head, index);  //找到第index个节点
    if (p == NULL)
    {
        cout << "要删除的为头节点" << endl;
        return false;
    }
    temp = index == 1 ? NULL : indexof(head, index - 1);  //找到要删除节点的前一个节点(前驱节点)
    temp->next = p->next;  //让要删除节点的前驱节点指向要删除节点的下一个节点
    free(p);  //释放要删除节点的内存
    return true;
}

#include "stacktp1.h"

int main()
{
    linkList* linkPtr;
    initlinkList(&linkPtr);
    insertDatabyHead(&linkPtr);
    showlinkList(&linkPtr);
    destroylinkListByHead(&linkPtr);

    system("pause");
    return 0;
}

运行结果：

3、链表尾插入法工作流程及测试

3.1调试deleteElementByIndex()函数的发现，使用二阶指针是要谨慎的

调试deleteElementByIndex()函数发现，主函数中的linkPtr经过showlinkList()函数之后已经成为了NULL空指针，原因在于所有的函数都使用二阶指针，一旦子函数中对实参进行了赋值的操作，

那么主函数中的实参也是会发生变化的，如：05)二阶指针作为形参，一阶指针的地址作为实参，改变子涵数(形参)实参的值会影响实参的值，所以使用二阶指针需谨慎~

改进的方法：

01）将实参传递给子涵数中的一个一阶指针，然后改变该一阶指针，这样就不会改变实参，如 04)二阶指针作为形参，一阶指针的地址作为实参，将形参赋给子函数中的一个变量，改变该便利的值不会影响实参的值

02）将部分函数中的二阶形参该为一阶形参

下面附上全部子函数使用二阶指针的例子，该例子中的showlinkList()函数会使linPtr成为NULL空指针，导致接下来继续调用linkPtr出错

#include "stacktp1.h"

int main()
{
    linkList* linkPtr;                   //创建链表的头结点
    initlinkList(&linkPtr);
    insertDatabyTail(&linkPtr);
    //showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以执行下一句会报错
    deleteElementByIndex(&linkPtr,5);  //删除头结点为linkPtr，链表中第二个数
    showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以不会执行下一个函数中的while循环,即不会删除链表
    destroylinkListByHead(&linkPtr);

    system("pause");
    return 0;
}

#include "stacktp1.h"

/*
01)链表的初始化(给头节点申请空间),所以在使用改函数的时候,只传入已创建结构的next指针即可;
02)使用指向指针的指针作为形参的原因在于要传入的参数是一个指针(要传入的参数是结构中的next指针),
   如果形参定义为一层指针,那么就会发生形参改变而实参并没有发生任何改变的情况。
*/
void initlinkList(linkList** head)
{
    if ((*head) == NULL)  //如果结构这的next指针为空，那么表明已经初始化完成;刚刚这里写成了 != 导致在插入数据的时候head->next访问不了
        return;
    *head = (linkList*)malloc(sizeof(linkList));  //给结构分配足够的内存空间
    (*head)->Element = 0;
    (*head)->next = NULL;  //head此时即是头节点也是尾节点，因为此时head指向了NULL
}

/*
01)链表的销毁
02)链表所有节点包括头结点都是动态申请的堆空间，使用完毕后必须手动释放，这里的销毁要把所有的节点空间全部释放;
03)方法一：从链表头开始遍历，也就是从前向后逐个释放每一个节点的空间
*/
void destroylinkListByHead(linkList** head)
{
    linkList* header = *head;
    linkList* p;
    while ( header != NULL)  //原来这里的条件是(*head)!=NULL，导致p->next指向了空指针;或者是循环了无数次
    {
        p = header;         //讲当前数据节点保存下来
        header = p->next;   //将下一个数据节点保存下来
        free(p);           //讲当前节点空间释放
        cout << "删除数据: " <<p->Element << endl;
    }
    free(header);  //释放头节点
    head = NULL;  //空间释放完的指针指向空指针
    cout << "链表已被删除完毕" << endl;
}

/*
01)方法二:从链表尾部向头部开始销毁，就不用临时保存
02)用递归遍历到最后一个结点，逐层向上返回，销毁每一个节点，顺序就是从头尾向头结点的顺序销毁。
*/
void destroylinkListByTail(linkList** head)
{
    if ((*head) == NULL)
        return;
    destroylinkListByTail(&((*head)->next));  //递归调用
    free(*head);
    head = NULL;
    cout << "链表已被删除完毕" << endl;
}

/*
01)向链表这插入数据
02)头插法：每次在头结点H的后面插入一个输入的数据，链表中的数据顺序和实际输入顺序相反
03)插入的过程主要是：先申请一个新的结点，链表不像数组一次性分配指定长度的空间，
   链表是需要增长一个就再申请一份，然后链接起来。申请完了之后给节点赋值，让新申请的节
   点指向头结点的next，也就是node->next = h->next，再让头结点指向这个新节点，
   H->next = node就完成插入操作。
04)传入的参数可以是头结点(头节点指向的是NULL)
05)传入的参数也可以是一个linkList结构的地址
06)以为此时是要向一个链表中插入数据，所以在使用malloc之后并没有释放内存
*/
void insertDatabyHead(linkList** head)
{
    linkList* node;  //新建一个需要插入的节点
    int x;
    cout << "请输入数据(-1结束)：" << endl;
    cin >> x;
    while (x != -1)
    {
        node = (linkList*) malloc(sizeof(linkList));    //为需要插入的节点分配空间    
        node->Element = x;
        //如果头节点指向的是NULL,所以下面这一句node->next换成NULL也可以
        node->next = (*head)->next; //使node成为head指向的一个节点之后的节点
        (*head)->next = node;  //使
        cout << "请输入数据(-1结束)：" << endl;  //接着输入数据
        cin >> x;
    }
}

/*
01)向链表这插入数据
02)尾插法：每次插入新的数据在链表的尾部插入就行，链表中的数据顺序和实际输入顺序相同
03)先找到链表的尾节点H->next == NULL，就是最后一个节点，同样插入就行。相比头插法，
   尾插法插入数据的时候如果链表不是一条空链表，得遍历先找到尾节点。
04)传入的参数的头结点(头节点指向的是NULL)
05)输入的参数是一个linkList结构的地址
*/

void insertDatabyTail(linkList** head)
{
    linkList* node;
    linkList* remove;
    int x;
    while ((*head)->next != NULL)  //如果head不是尾节点,那么找到尾节点,并使head成为尾节点；尾节点指向NULL
        (*head) = (*head)->next;
    remove = (*head);  //将head(尾节点)赋给remove,是remove也成为尾节点
    cout << "请输入要插入的数据(-1结束): " << endl;
    cin >> x;
    while (x != -1)
    {
        node = (linkList*)malloc(sizeof(linkList));
        node->Element = x;
        node->next = remove->next;  //此处也可以使用head->next，但使用remove是为了循环大计
        remove->next = node;  //此处也可以使用head->next，但是链表就是断的了
        remove = node;  //为下一次循环做准备
        cout << "请输入要插入的数据(-1结束): " << endl;
        cin >> x;
    }
}

/*
01)打印链表
02)输入为当前节点，或者是一个结构的地址
*/

void showlinkList(linkList** head)
{
    if ((*head)->next == NULL )  //如果当前节点是头节点，则指向下一个节点;以为头节点是没有数据的
        (*head) = (*head)->next;
    (*head) = (*head)->next;  //不显示头结点中的元素;上面那个if肯定不会被执行的,因为传入的参数是头结点,头结点的下一个节点肯定不是空(只要有数据)
    while ((*head) != NULL  )
    {
        cout << (*head)->Element << endl;
        (*head) = (*head)->next;    //注意！！这里已经将传入的头结点变成了NULL!!!!!且实参是头结点的地址,所以会改变实参的值
    }
}

/*
01)删除第index个节点
*/
/*返回第index个节点*/
linkList* indexof(linkList* head, int index)
{
    linkList* p = head;
    if (head->next == NULL)   //(*head)->next == NULL
    {
        cout << "输入的链表只有一个节点,且该节点为尾节点" << endl;
        return NULL;
    }
    int j;
    for (j = 0; p != NULL && j < index; j++)  //如果index等于1,则该for循环会忽略p=NULL的情况
        p = p->next;
    return j == index ? p : NULL;
}
/*删除第index个节点*/
int deleteElementByIndex(linkList** head, int index)
{
    linkList* p;
    linkList* temp;
    p = indexof(*head, index);  //找到第index个节点
    if (p == NULL)
    {
        cout << "要删除的为头节点" << endl;
        return false;
    }
    temp = index == 1 ? NULL : indexof(*head, index - 1);  //找到要删除节点的前一个节点(前驱节点)
    temp->next = p->next;  //让要删除节点的前驱节点指向要删除节点的下一个节点
    free(p);  //释放要删除节点的内存
    return true;
}

/*链表*/
#include <iostream>

using std::cin;
using std::cout;
using std::endl;

typedef int ElementType;

/*定义一个结构*/
struct linkList
{
    ElementType Element;  //定义结构中的一个数据(数据域)
    linkList* next;  //定义指向下一个结构的指针(指针域)
};

typedef struct linkList *PtrtoNode;  //PtrtoNode是一个类型,可以定义变量,且PtrtoNode是一个指针,指向结构体Node
typedef PtrtoNode List;  //为PtrtoNode起别名为List
typedef PtrtoNode Position;  //为PtrtoNode起别名为Position

void initlinkList(linkList** head);
void destroylinkListByHead(linkList** head);
void destroylinkListByTail(linkList** head);
void insertDatabyHead(linkList** head);
void insertDatabyTail(linkList** head);
void showlinkList(linkList** head);
linkList* indexof(linkList** head, int index);
int deleteElementByIndex(linkList** head, int index);

运行结果：

 3.2 改进（将showlinkList()中定义一个变量a，将形参赋值给变量a，改变变量a，而不改变实参即可）

如下图所示：

另外在destroylinkListByHead()函数中的while循环中加入了一个cout用于显示删除的数据

#include "stacktp1.h"

int main()
{
    linkList* linkPtr;                   //创建链表的头结点
    initlinkList(&linkPtr);
    insertDatabyTail(&linkPtr);
    showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以执行下一句会报错
    deleteElementByIndex(&linkPtr,5);  //删除头结点为linkPtr，链表中第二个数
    showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以不会执行下一个函数中的while循环,即不会删除链表
    destroylinkListByHead(&linkPtr);

    system("pause");
    return 0;
}

#include "stacktp1.h"

/*
01)链表的初始化(给头节点申请空间),所以在使用改函数的时候,只传入已创建结构的next指针即可;
02)使用指向指针的指针作为形参的原因在于要传入的参数是一个指针(要传入的参数是结构中的next指针),
   如果形参定义为一层指针,那么就会发生形参改变而实参并没有发生任何改变的情况。
*/
void initlinkList(linkList** head)
{
    if ((*head) == NULL)  //如果结构这的next指针为空，那么表明已经初始化完成;刚刚这里写成了 != 导致在插入数据的时候head->next访问不了
        return;
    *head = (linkList*)malloc(sizeof(linkList));  //给结构分配足够的内存空间
    (*head)->Element = 0;
    (*head)->next = NULL;  //head此时即是头节点也是尾节点，因为此时head指向了NULL
}

/*
01)链表的销毁
02)链表所有节点包括头结点都是动态申请的堆空间，使用完毕后必须手动释放，这里的销毁要把所有的节点空间全部释放;
03)方法一：从链表头开始遍历，也就是从前向后逐个释放每一个节点的空间
*/
void destroylinkListByHead(linkList** head)
{
    linkList* header = (*head)->next;  //由于传入的是头结点，所以越过头结点，保留头结点
    linkList* p;
    cout << "开始删除链表" << endl;
    while ( header != NULL)  //原来这里的条件是(*head)!=NULL，导致p->next指向了空指针;或者是循环了无数次
    {
        p = header;         //讲当前数据节点保存下来
        cout << "删除数据: " << p->Element << endl;
        header = p->next;   //将下一个数据节点保存下来
        free(p);           //讲当前节点空间释放
    }
    free(header);  //释放头节点
    head = NULL;  //空间释放完的指针指向空指针
    cout << "链表已被删除完毕" << endl;
}

/*
01)方法二:从链表尾部向头部开始销毁，就不用临时保存
02)用递归遍历到最后一个结点，逐层向上返回，销毁每一个节点，顺序就是从头尾向头结点的顺序销毁。
*/
void destroylinkListByTail(linkList** head)
{
    if ((*head) == NULL)
        return;
    destroylinkListByTail(&((*head)->next));  //递归调用
    free(*head);
    head = NULL;
    cout << "链表已被删除完毕" << endl;
}

/*
01)向链表这插入数据
02)头插法：每次在头结点H的后面插入一个输入的数据，链表中的数据顺序和实际输入顺序相反
03)插入的过程主要是：先申请一个新的结点，链表不像数组一次性分配指定长度的空间，
   链表是需要增长一个就再申请一份，然后链接起来。申请完了之后给节点赋值，让新申请的节
   点指向头结点的next，也就是node->next = h->next，再让头结点指向这个新节点，
   H->next = node就完成插入操作。
04)传入的参数可以是头结点(头节点指向的是NULL)
05)传入的参数也可以是一个linkList结构的地址
06)以为此时是要向一个链表中插入数据，所以在使用malloc之后并没有释放内存
*/
void insertDatabyHead(linkList** head)
{
    linkList* node;  //新建一个需要插入的节点
    int x;
    cout << "请输入数据(-1结束)：" << endl;
    cin >> x;
    while (x != -1)
    {
        node = (linkList*) malloc(sizeof(linkList));    //为需要插入的节点分配空间    
        node->Element = x;
        //如果头节点指向的是NULL,所以下面这一句node->next换成NULL也可以
        node->next = (*head)->next; //使node成为head指向的一个节点之后的节点
        (*head)->next = node;  //使
        cout << "请输入数据(-1结束)：" << endl;  //接着输入数据
        cin >> x;
    }
}

/*
01)向链表这插入数据
02)尾插法：每次插入新的数据在链表的尾部插入就行，链表中的数据顺序和实际输入顺序相同
03)先找到链表的尾节点H->next == NULL，就是最后一个节点，同样插入就行。相比头插法，
   尾插法插入数据的时候如果链表不是一条空链表，得遍历先找到尾节点。
04)传入的参数的头结点(头节点指向的是NULL)
05)输入的参数是一个linkList结构的地址
*/

void insertDatabyTail(linkList** head)
{
    linkList* node;
    linkList* remove;
    int x;
    while ((*head)->next != NULL)  //如果head不是尾节点,那么找到尾节点,并使head成为尾节点；尾节点指向NULL
        (*head) = (*head)->next;
    remove = (*head);  //将head(尾节点)赋给remove,是remove也成为尾节点
    cout << "请输入要插入的数据(-1结束): " << endl;
    cin >> x;
    while (x != -1)
    {
        node = (linkList*)malloc(sizeof(linkList));
        node->Element = x;
        node->next = remove->next;  //此处也可以使用head->next，但使用remove是为了循环大计
        remove->next = node;  //此处也可以使用head->next，但是链表就是断的了
        remove = node;  //为下一次循环做准备
        cout << "请输入要插入的数据(-1结束): " << endl;
        cin >> x;
    }
}

/*
01)打印链表
02)输入为当前节点，或者是一个结构的地址
*/

void showlinkList(linkList** head)
{
    linkList* header = *head;
    if (header->next == NULL )  //如果当前节点是头节点，则指向下一个节点;以为头节点是没有数据的
        header = header->next;
    header = header->next;  //不显示头结点中的元素;上面那个if肯定不会被执行的,因为传入的参数是头结点,头结点的下一个节点肯定不是空(只要有数据)
    while (header != NULL  )
    {
        cout << header->Element << endl;
        header = header->next;    //注意！！这里已经将传入的头结点变成了NULL!!!!!且实参是头结点的地址,所以会改变实参的值
    }
}

/*
01)删除第index个节点
*/
/*返回第index个节点*/
linkList* indexof(linkList* head, int index)
{
    linkList* p = head;
    if (head->next == NULL)   //(*head)->next == NULL
    {
        cout << "输入的链表只有一个节点,且该节点为尾节点" << endl;
        return NULL;
    }
    int j;
    for (j = 0; p != NULL && j < index; j++)  //如果index等于1,则该for循环会忽略p=NULL的情况
        p = p->next;
    return j == index ? p : NULL;
}
/*删除第index个节点*/
int deleteElementByIndex(linkList** head, int index)
{
    linkList* p;
    linkList* temp;
    p = indexof(*head, index);  //找到第index个节点
    if (p == NULL)
    {
        cout << "要删除的为头节点" << endl;
        return false;
    }
    temp = index == 1 ? NULL : indexof(*head, index - 1);  //找到要删除节点的前一个节点(前驱节点)
    temp->next = p->next;  //让要删除节点的前驱节点指向要删除节点的下一个节点
    cout << "开始删除第" << index << "个节点" << endl;
    free(p);  //释放要删除节点的内存
    return true;
}

/*链表*/
#include <iostream>

using std::cin;
using std::cout;
using std::endl;

typedef int ElementType;

/*定义一个结构*/
struct linkList
{
    ElementType Element;  //定义结构中的一个数据(数据域)
    linkList* next;  //定义指向下一个结构的指针(指针域)
};

typedef struct linkList *PtrtoNode;  //PtrtoNode是一个类型,可以定义变量,且PtrtoNode是一个指针,指向结构体Node
typedef PtrtoNode List;  //为PtrtoNode起别名为List
typedef PtrtoNode Position;  //为PtrtoNode起别名为Position

void initlinkList(linkList** head);
void destroylinkListByHead(linkList** head);
void destroylinkListByTail(linkList** head);
void insertDatabyHead(linkList** head);
void insertDatabyTail(linkList** head);
void showlinkList(linkList** head);
linkList* indexof(linkList* head, int index);
int deleteElementByIndex(linkList** head, int index);

执行结果：

3.3链表翻转(20200321)

指针反转原理及代码：

题目描述
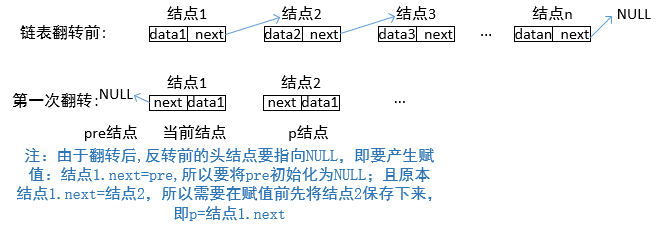
输入一个链表，反转链表后，输出新链表的表头。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
            val(x), next(NULL) {
    }
};*/
class Solution {
public:
    ListNode* ReverseList(ListNode* pHead)
    {
        ListNode* pre=NULL;  //初始化当前结点的前一个结点为NULL,反转后,头结点的next指针指向NULL
        ListNode* p;         //由于要操作pHead->next,所以需要保存当前节点的下一个节点
        
        while(pHead!=NULL)
        {
            p=pHead->next;     //保存当前节点的下一个节点
            pHead->next=pre;   //当前节点指向当前节点的前一个节点
            pre=pHead;         //更新当前节点的前一个节点为当前节点
            pHead=p;           //更新当前节点为当前节点的下一个节点
        }
        return pre;
    }
};

牛客网地址：https://www.nowcoder.com/practice/75e878df47f24fdc9dc3e400ec6058ca?tpId=13&tqId=11168&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

3.4合并两个有序的链表

 leetcode题目链接

/**
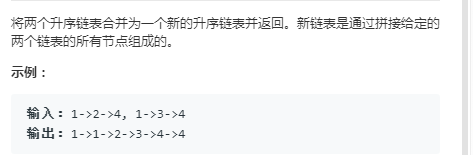
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if(l1==NULL)
            return l2;
        if(l2==NULL)
            return l1;
        ListNode* head=new ListNode(sizeof(ListNode));
        ListNode* t=head;  //要将l1和l2和并后的头结点保存下来,而且head->next才是l1和l2中的数据,即返回值必须为head->next
        while(l1!=NULL && l2!=NULL){
            if(l1->val < l2->val){
                t->next=l1;
                l1=l1->next;
            }
            else{
                t->next=l2;
                l2=l2->next;
            }
            t=t->next;      //在这里如果是head=head->next,那么头节点就保存不下来了,所以找一个中间变量
        }//执行完while循环之后l1和l2总有一个为空的
        if(l1!=NULL)
            t->next=l1;
        else if(l2!=NULL)
            t->next=l2;
        return head->next;
    }
};

3.5k个为一组反转链表

题目：

/**
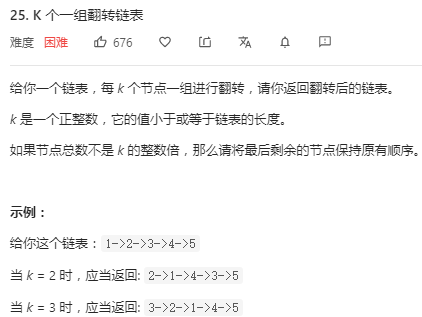
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* dummy=new ListNode(0);
        dummy->next=head;                   //相当于创建一个虚头节点(在头节点的前面)
        ListNode* pPre=dummy;
        ListNode* KNodeNext=head;
        while(pPre!=nullptr){
            //找到第k的节点的下一个节点
            for(int i=0;i<k;++i){
                if(KNode==nullptr)
                    return dummy->next;
                KNodeNext=KNodeNext->next;
            }
            //pTmp为k个为一组的头节点
            ListNode* pTmp=pPre->next;
            /*反转pTmp节点和KNode节点之间的节点,第一次返回值返回给了dummy->next
             * 虽然传入的是KNodeNext,但是在子函数中最后head=KNodeNext的时候不会执行
             * 所以反转的是[head,KNode]之间的节点
             * 举例传入a->b->c->d返回节点顺序为null<-a<-b<-c，且返回值为c节点
            */
            pPre->next=reverse(pTmp,KNodeNext);
            /*反转后pTmp为[pTmp结点,KNode节点]的尾节点,将该节点和KNode的下一个节点连接上
             *假如完整的链表顺序为a->b->c->d->e 且k=3
             *则首先将a->b->c反转成c->b->a,此时pTmp还是指向a节点的,KNodeNext指向d结点
             *那么将pTmp->next=KNodeNext即可完成连接
            */
            pTmp->next=KNodeNext;
            //更新pPre和KNode指向下一组的头节点
            pPre=pTmp;
        }
        return dummy->next;
    }

    //将head节点和tail节点之间的节点反转(a->b->c->d->NULL)变成(NULL<-a<-b<-c<-d)
    ListNode* reverse(ListNode* head,ListNode* tail){
        if(head==nullptr){
            return head;
        }
        ListNode* pre=nullptr;
        ListNode* pNext;
        while(head!=tail){
            pNext=head->next;
            head->next=pre;     //改变头节点的指向
            pre=head;
            head=pNext;
        }
        return pre;            //返回d节点
    }
};

题目链接

二刷：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* dummy=new ListNode(sizeof(ListNode));
        dummy->next=head;
        ListNode* pre=dummy;         //pre和dummy相当于头节点的前一个节点,所以要用pre->next;第二遍刷的时候也没有意识到pre节点相当于是一个头结点或者是k个为一组的头节点的前一个节点
        ListNode* KNodeNext=head;
        while(pre!=nullptr){
            for(int i=0;i<k;++i){
                if(KNodeNext==nullptr)
                    return dummy->next;
                //找到第K个节点的下一个节点;第二遍刷的时候没有意识到这里找到的是第K个节点的下一个节点
                KNodeNext=KNodeNext->next;    
            }
            ListNode* KGrooupHead=pre->next;
            pre->next=reverse(KGrooupHead,KNodeNext);
            KGrooupHead->next=KNodeNext;       //连接
            pre=KGrooupHead;
        }
        return dummy->next;
    }

    //翻转
    ListNode* reverse(ListNode* head,ListNode* tail){
        if(head==nullptr)
            return nullptr;
        ListNode* pre=nullptr;
        ListNode* pNext;
        while(head!=tail){
            pNext=head->next;    //保存头节点的下一个节点
            head->next=pre;
            pre=head;
            head=pNext;
        }
        return pre;
    }
};

 

 

4、双向链表  m44

给每个元素附加两个指针域，一个存储前一个元素的地址，一个存储下一个元素的地址。这种链表称为双向链表，如下图所示：

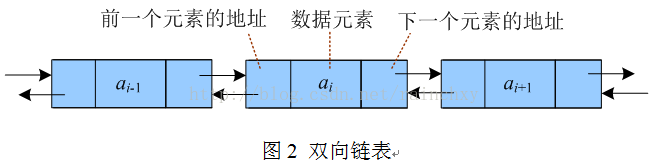
  (1) 链表初始化和创建  m441

初始化和创建双向链表的代码：

#pragma once

typedef int Type;


struct doubleLinklist
{
    Type data;                //存储数据
    doubleLinklist* prior;    //前向指针
    doubleLinklist* next;     //后继指针
};

typedef struct doubleLinklist* PtrNode;

void initdoubleLinklist(doubleLinklist** head);
void creeatdoubleLinklist(doubleLinklist** head);  //和单向链表的insert是一样的,连续的插入并不只是插入一个数据

#include <iostream>
#include "doubleLinkList.h"

using std::cin;
using std::cout;
using std::endl;

void initdoubleLinklist(doubleLinklist** head)
{
    if ((*head) == NULL)
        return;
    (*head) = new doubleLinklist;
    (*head)->data = 0;
    (*head)->prior = NULL;
    (*head)->next = NULL;
}
void creeatdoubleLinklist(doubleLinklist** head)
{
    doubleLinklist* node;
    cout << "请输入一个Type类型的数据(-1结束): " << endl;
    Type x;
    cin >> x;
    while (x != -1)
    {
        node = new doubleLinklist;
        node->data = x;
        if ((*head)->next != NULL)
            (*head)->next->prior = node;
        node->next = (*head)->next;
        node->prior = (*head);
        (*head)->next = node;
        cout << "请输入一个Type类型的数据(-1结束): " << endl;
        cin >> x;
    }
}

/*双向链表测试*/
#include <iostream>          //for system()
#include "doubleLinkList.h"

void showAll(doubleLinklist** head)
{
    doubleLinklist* header = (*head)->next;  //越过头节点
    while (header != NULL)
    {
        cout << header->data << endl;
        header = header->next;
    }
}

int main()
{
    doubleLinklist* PtrLinklist;
    initdoubleLinklist(&PtrLinklist);
    creeatdoubleLinklist(&PtrLinklist);
    showAll(&PtrLinklist);

    system("pause");
    return 0;
}

运行结果：

(2) 在链表的第i个位置插入数据data

“在链表的第i个位置插入数据data”的插入过程其实和创建链表插入第2个数据步骤是一样的，具体参考图

#pragma once

typedef int Type;


struct doubleLinklist
{
    Type data;                //存储数据
    doubleLinklist* prior;    //前向指针
    doubleLinklist* next;     //后继指针
};

typedef struct doubleLinklist* PtrNode;

void initDULinklist(doubleLinklist** head);
void creeatDULinklistByHead(doubleLinklist** head);  //和单向链表的insert是一样的,连续的插入并不只是插入一个数据
void insertToDULinkList(doubleLinklist** head, int i, int data);

void showAllByNext(doubleLinklist** head);

#include <iostream>
#include "doubleLinkList.h"

using std::cin;
using std::cout;
using std::endl;

/*双向链表初始化*/
void initDULinklist(doubleLinklist** head)
{
    if ((*head) == NULL)
        return;
    (*head) = new doubleLinklist;
    (*head)->data = 0;
    (*head)->prior = NULL;
    (*head)->next = NULL;
}

/*头插入创造双向链表*/
void creeatDULinklistByHead(doubleLinklist** head)
{
    doubleLinklist* node;
    cout << "请输入一个您设置类型的数据(-1结束): " << endl;
    Type x;
    cin >> x;
    while (x != -1)
    {
        node = new doubleLinklist;
        node->data = x;
        if ((*head)->next != NULL)
            (*head)->next->prior = node;
        node->next = (*head)->next;
        node->prior = (*head);
        (*head)->next = node;
        cout << "请输入一个Type类型的数据(-1结束): " << endl;
        cin >> x;
    }
}

/*在链表的第i个位置插入数据data*/
void insertToDULinkList(doubleLinklist** head, int i, int data)
{
    doubleLinklist* header = (*head)->next;  //越过头节点
    doubleLinklist* node;            //创建新插入的节点
    int j=1;
    while (header != NULL && j < i)  //找到第i个节点
    {
        header = header->next;
        j++;
    }
    node = new doubleLinklist;    //为新创建的节点分配空间
    node->data = data;
    header->next->prior = node;
    node->next = header->next;
    node->prior = header;
    header->next = node;
}

void showAllByNext(doubleLinklist** head)
{
    doubleLinklist* header = (*head)->next;  //越过头节点
    while (header != NULL)
    {
        cout << header->data << endl;
        header = header->next;
    }
}

//#include "stacktp1.h"
//
//int main()
//{
//    linkList* linkPtr;                   //创建链表的头结点
//    initlinkList(&linkPtr);
//    insertDatabyTail(&linkPtr);
//    showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以执行下一句会报错
//    deleteElementByIndex(&linkPtr,5);  //删除头结点为linkPtr，链表中第二个数
//    showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以不会执行下一个函数中的while循环,即不会删除链表
//    destroylinkListByTail(&linkPtr);
//
//    system("pause");
//    return 0;
//}
//

/*最大堆测试*/
//#include "PriorityQueue.h"
//
//int main()
//{
//    {
//        int arr[] = { 37,26,14,52,69,78,98,48,69,70 };
//        int n = sizeof(arr) / sizeof(arr[0]);  //获取数组元素个数的新方法
//        Heap<int>* heap = new Heap<int>(20);   //新建指向类模板的指针，不新建指针也是可以的如Heap<int> heap(20);
//        for (int i = 0; i < n; i++)
//        {
//            heap->insert(arr[i]);
//        }
//        heap->showHeap();
//        cout << endl;
//
//        cout << "添加元素100" << endl;
//        heap->insert(100);
//        heap->showHeap();
//        cout << endl;
//
//        cout << "删除元素78" << endl;
//        heap->remove(78);
//        heap->showHeap();
//    }
//
//    system("pause");
//    return 0;
//}

//#include <iostream>
//#include <cstdio>
//#include <queue>
//
//using namespace std;
//
//int main()
//{
//    priority_queue<int> q;
//    int arr[] = { 37,26,14,52,69,78,98,48,69,70 };
//    int n = sizeof(arr) / sizeof(arr[0]);  //获取数组元素个数的新方法
//    for (int i = 0; i < n; i++)
//    {
//        q.push(arr[i]);
//    }
//    while (!q.empty())
//    {
//        cout << q.top() << " " << endl;
//        q.pop();
//    }
//
//    system("pause");
//    return 0;
//}

//#include <iostream>
//
//using std::cout;
//using std::endl;
//
//int main()
//{
//    int i = 8;
//    int arr[] = { 1,2,3,4,5,6,7,8,9 };
//
//    //cout << arr[i--] << endl;    //打印9  先使用后修改
//    //cout << arr[i--] << endl;    //打印8
//
//    //cout << arr[--i] << endl;    //打印8    先修改后使用
//    //cout << arr[--i] << endl;    //打印7
//    //cout << endl;
//    //cout << i;    //此时i=6
//
//    int c[] = { 2,3,4,5 };
//    int j, *p = c, *q = c;
//    for (j = 0; j < 4; j++)
//    {
//        printf(" %d", *c);
//        ++q;
//    }
//    for (j = 0; j < 4; j++)
//    {
//        printf(" %d", *p);
//        ++p;
//    }
//
//    system("pause");
//    return 0;
//}

//#include "queue.h"
//
//int main()
//{
//    int x;
//    int temp;
//    int size = 6;
//    Queue<int>* queue = new Queue<int>(size);
//    cout << "请输入一个整数，按字母q结束：";
//    cin >> x;
//    while (x != 0)
//    {
//        queue->enqueue(x);
//        cout << "请输入一个整数，按字母q结束：";
//        cin >> x;
//    }
//    cout << "队中元素个数为：" << queue->queueLength() << endl;
//    int n = queue->queueLength();
//    for (int i = 0; i <= n; i++)
//    {
//        queue->dequeue(temp);
//        cout << "出队的元素是：" << temp << endl;
//    }
//    /*queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;*/
//
//    system("pause");
//    return 0;
//}

//#include "queue.h"
//
//int main()
//{
//    int x;
//    int temp;
//    int size = 6;
//    Queue<int>* queue = new Queue<int>(size);
//    cout << "请输入一个整数，按字母q结束：";
//    cin >> x;
//    queue->enqueue(x);
//    cout << "请输入一个整数，按字母q结束：";
//    cin >> x;
//    queue->enqueue(x);
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//
//    system("pause");
//    return 0;
//}

/*双向链表测试*/
#include <iostream>          //for system()
#include "doubleLinkList.h"

using std::cout;
using std::endl;

int main()
{
    doubleLinklist* PtrLinklist;
    initDULinklist(&PtrLinklist);
    creeatDULinklistByHead(&PtrLinklist);
    showAllByNext(&PtrLinklist);
    cout << "开始插入数据" << endl;
    insertToDULinkList(&PtrLinklist, 2, 45);
    showAllByNext(&PtrLinklist);

    system("pause");
    return 0;
}

运行结果(该方法是先的是在第二个节点之后插入新数据，把3所在的节点当做是第一个节点)：

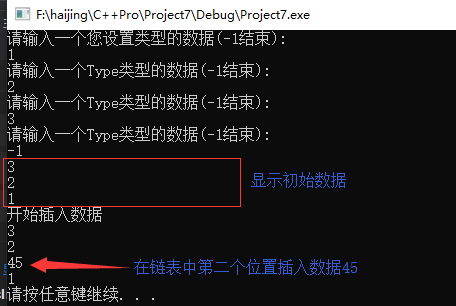
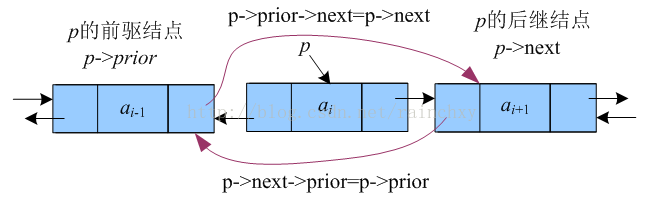
(3) 删除链表中的第i个节点

删除一个结点，实际上是把这个结点跳过去。要想跳过第i个结点，可以先找到第i个结点。然后修改指针，如图：

#pragma once

typedef int Type;


struct doubleLinklist
{
    Type data;                //存储数据
    doubleLinklist* prior;    //前向指针
    doubleLinklist* next;     //后继指针
};

typedef struct doubleLinklist* PtrNode;

void initDULinklist(doubleLinklist** head);
void creeatDULinklistByHead(doubleLinklist** head);  //和单向链表的insert是一样的,连续的插入并不只是插入一个数据
void insertToDULinkList(doubleLinklist** head, int i, int data);
void deleteOneNode(doubleLinklist** head, int i);    //删除第i个节点

void showAllByNext(doubleLinklist** head);

#include <iostream>
#include "doubleLinkList.h"

using std::cin;
using std::cout;
using std::endl;

/*双向链表初始化*/
void initDULinklist(doubleLinklist** head)
{
    if ((*head) == NULL)
        return;
    (*head) = new doubleLinklist;
    (*head)->data = 0;
    (*head)->prior = NULL;
    (*head)->next = NULL;
}

/*头插入创造双向链表*/
void creeatDULinklistByHead(doubleLinklist** head)
{
    doubleLinklist* node;
    cout << "请输入一个您设置类型的数据(-1结束): ";
    Type x;
    cin >> x;
    while (x != -1)
    {
        node = new doubleLinklist;
        node->data = x;
        if ((*head)->next != NULL)
            (*head)->next->prior = node;
        node->next = (*head)->next;
        node->prior = (*head);
        (*head)->next = node;
        cout << "请输入一个您设置类型的数据(-1结束): ";
        cin >> x;
    }
}

/*在链表的第i个位置插入数据data*/
void insertToDULinkList(doubleLinklist** head, int i, int data)
{
    doubleLinklist* header = (*head)->next;  //越过头节点 此时header是第一个节点,所以j=1
    doubleLinklist* node;            //创建新插入的节点
    int j=1;
    while (header != NULL && j < i)  //找到第i个节点
    {
        header = header->next;
        j++;
    }
    node = new doubleLinklist;    //为新创建的节点分配空间
    node->data = data;
    header->next->prior = node;
    node->next = header->next;
    node->prior = header;
    header->next = node;
}

/*删除第i个节点*/
void deleteOneNode(doubleLinklist** head, int i)
{
    doubleLinklist* header = (*head)->next;  //越过头节点(第0个节点)
    int j = 1;                               //
    while (header != NULL && j < i)          //找到第i个节点
    {
        header = header->next;
        j++;
    }
    header->next->prior = header->prior;
    header->prior->next = header->next;
    delete header;                        //删除第i个节点
}

void showAllByNext(doubleLinklist** head)
{
    doubleLinklist* header = (*head)->next;  //越过头节点
    while (header != NULL)
    {
        cout << header->data << endl;
        header = header->next;
    }
}

//#include "stacktp1.h"
//
//int main()
//{
//    linkList* linkPtr;                   //创建链表的头结点
//    initlinkList(&linkPtr);
//    insertDatabyTail(&linkPtr);
//    showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以执行下一句会报错
//    deleteElementByIndex(&linkPtr,5);  //删除头结点为linkPtr，链表中第二个数
//    showlinkList(&linkPtr);           //此句已经使linkPt成为了尾节点,所以不会执行下一个函数中的while循环,即不会删除链表
//    destroylinkListByTail(&linkPtr);
//
//    system("pause");
//    return 0;
//}
//

/*最大堆测试*/
//#include "PriorityQueue.h"
//
//int main()
//{
//    {
//        int arr[] = { 37,26,14,52,69,78,98,48,69,70 };
//        int n = sizeof(arr) / sizeof(arr[0]);  //获取数组元素个数的新方法
//        Heap<int>* heap = new Heap<int>(20);   //新建指向类模板的指针，不新建指针也是可以的如Heap<int> heap(20);
//        for (int i = 0; i < n; i++)
//        {
//            heap->insert(arr[i]);
//        }
//        heap->showHeap();
//        cout << endl;
//
//        cout << "添加元素100" << endl;
//        heap->insert(100);
//        heap->showHeap();
//        cout << endl;
//
//        cout << "删除元素78" << endl;
//        heap->remove(78);
//        heap->showHeap();
//    }
//
//    system("pause");
//    return 0;
//}

//#include <iostream>
//#include <cstdio>
//#include <queue>
//
//using namespace std;
//
//int main()
//{
//    priority_queue<int> q;
//    int arr[] = { 37,26,14,52,69,78,98,48,69,70 };
//    int n = sizeof(arr) / sizeof(arr[0]);  //获取数组元素个数的新方法
//    for (int i = 0; i < n; i++)
//    {
//        q.push(arr[i]);
//    }
//    while (!q.empty())
//    {
//        cout << q.top() << " " << endl;
//        q.pop();
//    }
//
//    system("pause");
//    return 0;
//}

//#include <iostream>
//
//using std::cout;
//using std::endl;
//
//int main()
//{
//    int i = 8;
//    int arr[] = { 1,2,3,4,5,6,7,8,9 };
//
//    //cout << arr[i--] << endl;    //打印9  先使用后修改
//    //cout << arr[i--] << endl;    //打印8
//
//    //cout << arr[--i] << endl;    //打印8    先修改后使用
//    //cout << arr[--i] << endl;    //打印7
//    //cout << endl;
//    //cout << i;    //此时i=6
//
//    int c[] = { 2,3,4,5 };
//    int j, *p = c, *q = c;
//    for (j = 0; j < 4; j++)
//    {
//        printf(" %d", *c);
//        ++q;
//    }
//    for (j = 0; j < 4; j++)
//    {
//        printf(" %d", *p);
//        ++p;
//    }
//
//    system("pause");
//    return 0;
//}

//#include "queue.h"
//
//int main()
//{
//    int x;
//    int temp;
//    int size = 6;
//    Queue<int>* queue = new Queue<int>(size);
//    cout << "请输入一个整数，按字母q结束：";
//    cin >> x;
//    while (x != 0)
//    {
//        queue->enqueue(x);
//        cout << "请输入一个整数，按字母q结束：";
//        cin >> x;
//    }
//    cout << "队中元素个数为：" << queue->queueLength() << endl;
//    int n = queue->queueLength();
//    for (int i = 0; i <= n; i++)
//    {
//        queue->dequeue(temp);
//        cout << "出队的元素是：" << temp << endl;
//    }
//    /*queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;*/
//
//    system("pause");
//    return 0;
//}

//#include "queue.h"
//
//int main()
//{
//    int x;
//    int temp;
//    int size = 6;
//    Queue<int>* queue = new Queue<int>(size);
//    cout << "请输入一个整数，按字母q结束：";
//    cin >> x;
//    queue->enqueue(x);
//    cout << "请输入一个整数，按字母q结束：";
//    cin >> x;
//    queue->enqueue(x);
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//    queue->dequeue(temp);
//    cout << "出队的元素是：" << temp << endl;
//
//    system("pause");
//    return 0;
//}

/*双向链表测试*/
#include <iostream>          //for system()
#include "doubleLinkList.h"

using std::cout;
using std::endl;

int main()
{
    doubleLinklist* PtrLinklist;
    initDULinklist(&PtrLinklist);
    creeatDULinklistByHead(&PtrLinklist);
    showAllByNext(&PtrLinklist);

    cout << "开始插入数据" << endl;
    insertToDULinkList(&PtrLinklist, 2, 45);
    showAllByNext(&PtrLinklist);

    cout << "开始删除第1个节点" << endl;
    deleteOneNode(&PtrLinklist, 1);
    showAllByNext(&PtrLinklist);

    cout << "再删除第2个节点" << endl;
    deleteOneNode(&PtrLinklist, 2);
    showAllByNext(&PtrLinklist);


    system("pause");
    return 0;
}

运行结果：

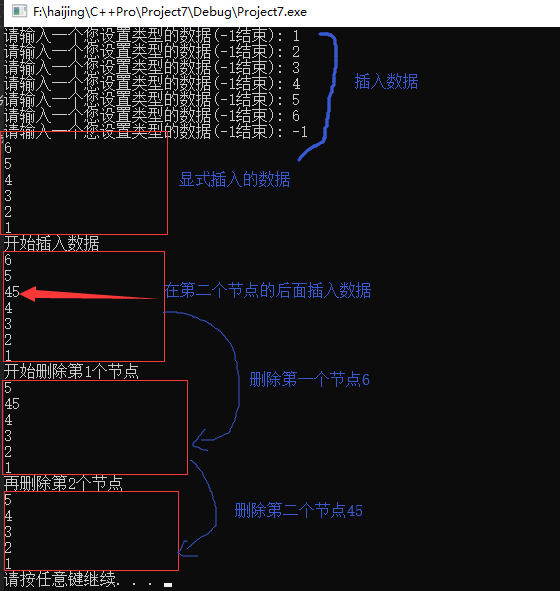
(4) 删除所有元素

删除元素借鉴了单向链表删除所有元素的方法

#pragma once

typedef int Type;


struct doubleLinklist
{
    Type data;                //存储数据
    doubleLinklist* prior;    //前向指针
    doubleLinklist* next;     //后继指针
};

typedef struct doubleLinklist* PtrNode;

void initDULinklist(doubleLinklist** head);
void creeatDULinklistByHead(doubleLinklist** head);  //和单向链表的insert是一样的,连续的插入并不只是插入一个数据
void insertToDULinkList(doubleLinklist** head, int i, int data);
void deleteOneNode(doubleLinklist** head, int i);    //删除第i个节点
void deleteAll(doubleLinklist** head);               //删除所有节点

void showAllByNext(doubleLinklist** head);

#include <iostream>
#include "doubleLinkList.h"

using std::cin;
using std::cout;
using std::endl;

/*双向链表初始化*/
void initDULinklist(doubleLinklist** head)
{
    if ((*head) == NULL)
        return;
    (*head) = new doubleLinklist;
    (*head)->data = 0;
    (*head)->prior = NULL;
    (*head)->next = NULL;
}

/*头插入创造双向链表*/
void creeatDULinklistByHead(doubleLinklist** head)
{
    doubleLinklist* node;
    cout << "请输入一个您设置类型的数据(-1结束): ";
    Type x;
    cin >> x;
    while (x != -1)
    {
        node = new doubleLinklist;
        node->data = x;
        if ((*head)->next != NULL)
            (*head)->next->prior = node;
        node->next = (*head)->next;
        node->prior = (*head);
        (*head)->next = node;
        cout << "请输入一个您设置类型的数据(-1结束): ";
        cin >> x;
    }
}

/*在链表的第i个位置插入数据data*/
void insertToDULinkList(doubleLinklist** head, int i, int data)
{
    doubleLinklist* header = (*head)->next;  //越过头节点 此时header是第一个节点,所以j=1
    doubleLinklist* node;            //创建新插入的节点
    int j=1;
    while (header != NULL && j < i)  //找到第i个节点
    {
        header = header->next;
        j++;
    }
    node = new doubleLinklist;    //为新创建的节点分配空间
    node->data = data;
    header->next->prior = node;
    node->next = header->next;
    node->prior = header;
    header->next = node;
}

/*删除第i个节点*/
void deleteOneNode(doubleLinklist** head, int i)
{
    doubleLinklist* header = (*head)->next;  //越过头节点(第0个节点)
    int j = 1;                               //
    while (header != NULL && j < i)          //找到第i个节点
    {
        header = header->next;
        j++;
    }
    header->next->prior = header->prior;
    header->prior->next = header->next;
    delete header;                        //删除第i个节点
}

/*删除所有节点*/
void deleteAll(doubleLinklist** head)
{
    doubleLinklist* header = (*head)->next;
    doubleLinklist* p;
    while (header != NULL)
    {
        p = header;                              //必须找一个中间变量,否则会发生访问权限错误
        cout << "删除元素: " << p->data <<endl;
        header = p->next;
        delete(p);
    }
    delete(header);  //删除头结点
    cout << "所有节点删除完毕" << endl;
}

void showAllByNext(doubleLinklist** head)
{
    doubleLinklist* header = (*head)->next;  //越过头节点
    while (header != NULL)
    {
        cout << header->data << endl;
        header = header->next;
    }
}

/*双向链表测试*/
#include <iostream>          //for system()
#include "doubleLinkList.h"

using std::cout;
using std::endl;

int main()
{
    doubleLinklist* PtrLinklist;
    initDULinklist(&PtrLinklist);
    creeatDULinklistByHead(&PtrLinklist);
    showAllByNext(&PtrLinklist);

    cout << "开始插入数据" << endl;
    insertToDULinkList(&PtrLinklist, 2, 45);
    showAllByNext(&PtrLinklist);

    cout << "开始删除第1个节点" << endl;
    deleteOneNode(&PtrLinklist, 1);
    showAllByNext(&PtrLinklist);

    cout << "再删除第2个节点" << endl;
    deleteOneNode(&PtrLinklist, 2);
    showAllByNext(&PtrLinklist);

    deleteAll(&PtrLinklist);


    system("pause");
    return 0;
}

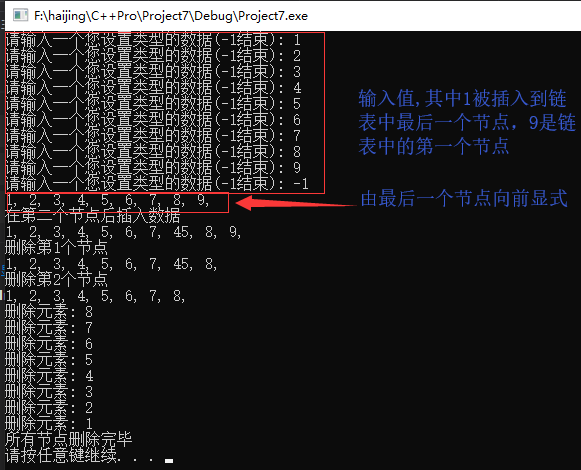
运行结果：

(5) 最后的修改

#include <iostream>
#include "doubleLinkList.h"

using std::cin;
using std::cout;
using std::endl;

/*双向链表初始化*/
void initDULinklist(doubleLinklist** head)
{
    if ((*head) == NULL)
        return;
    (*head) = new doubleLinklist;
    (*head)->data = 0;
    (*head)->prior = NULL;
    (*head)->next = NULL;
}

/*头插入创造双向链表*/
void creeatDULinklistByHead(doubleLinklist** head)
{
    doubleLinklist* node;
    cout << "请输入一个您设置类型的数据(-1结束): ";
    Type x;
    cin >> x;
    while (x != -1)
    {
        node = new doubleLinklist;
        node->data = x;
        if ((*head)->next != NULL)
            (*head)->next->prior = node;
        node->next = (*head)->next;
        node->prior = (*head);
        (*head)->next = node;
        cout << "请输入一个您设置类型的数据(-1结束): ";
        cin >> x;
    }
}

/*在链表的第i个位置插入数据data*/
void insertToDULinkList(doubleLinklist** head, int i, int data)
{
    doubleLinklist* header = (*head)->next;  //越过头节点 此时header是第一个节点,所以j=1
    doubleLinklist* node;            //创建新插入的节点
    int j=1;
    while (header != NULL && j < i)  //找到第i个节点
    {
        header = header->next;
        j++;
    }
    node = new doubleLinklist;    //为新创建的节点分配空间
    node->data = data;
    header->next->prior = node;
    node->next = header->next;
    node->prior = header;
    header->next = node;
}

/*删除第i个节点*/
void deleteOneNode(doubleLinklist** head, int i)
{
    doubleLinklist* header = (*head)->next;  //越过头节点(第0个节点)
    int j = 1;                               //
    while (header != NULL && j < i)          //找到第i个节点
    {
        header = header->next;
        j++;
    }
    if (header->next == NULL)
    {
        cout << "deleteOneNode()子程序中出现了header->next=NULL的情况！" << endl;
        return;  //退出程序
    }
    header->next->prior = header->prior;
    header->prior->next = header->next;
    delete header;                        //删除第i个节点
}

/*删除所有节点*/
void deleteAll(doubleLinklist** head)
{
    doubleLinklist* header = (*head)->next;
    doubleLinklist* p;
    while (header != NULL)
    {
        p = header;                              //必须找一个中间变量,否则会发生访问权限错误
        cout << "删除元素: " << p->data <<endl;
        header = p->next;
        delete(p);
    }
    delete(header);  //删除头结点
    cout << "所有节点删除完毕" << endl;
}

void showAllByNext(doubleLinklist** head)
{
    doubleLinklist* header = (*head)->next;  //越过头节点
    while (header != NULL)
    {
        cout << header->data << ", ";
        header = header->next;
    }
    cout << endl;
}

void showAllByPrior(doubleLinklist** head)
{
    doubleLinklist* header = *head;
    while (header->next != NULL)     //找到尾节点(使header成为尾结点)
        header = header->next;
    while (header->prior != NULL)    //不显示头结点的数据
    {
        cout << header->data <<", ";
        header = header->prior;
    }
    cout << endl;
}

#pragma once

typedef int Type;


struct doubleLinklist
{
    Type data;                //存储数据
    doubleLinklist* prior;    //前向指针
    doubleLinklist* next;     //后继指针
};

typedef struct doubleLinklist* PtrNode;

void initDULinklist(doubleLinklist** head);
void creeatDULinklistByHead(doubleLinklist** head);  //和单向链表的insert是一样的,连续的插入并不只是插入一个数据
void insertToDULinkList(doubleLinklist** head, int i, int data);
void deleteOneNode(doubleLinklist** head, int i);    //删除第i个节点
void deleteAll(doubleLinklist** head);               //删除所有节点

void showAllByNext(doubleLinklist** head);
void showAllByPrior(doubleLinklist** head);

/*双向链表测试*/
#include <iostream>          //for system()
#include "doubleLinkList.h"

using std::cout;
using std::endl;

int main()
{
    doubleLinklist* PtrLinklist;
    initDULinklist(&PtrLinklist);
    creeatDULinklistByHead(&PtrLinklist);
    showAllByPrior(&PtrLinklist);

    cout << "在第二个节点后插入数据" << endl;
    insertToDULinkList(&PtrLinklist, 2, 45);
    showAllByPrior(&PtrLinklist);

    cout << "删除第1个节点" << endl;
    deleteOneNode(&PtrLinklist, 1);
    showAllByPrior(&PtrLinklist);

    cout << "删除第2个节点" << endl;
    deleteOneNode(&PtrLinklist, 2);
    showAllByPrior(&PtrLinklist);

    deleteAll(&PtrLinklist);


    system("pause");
    return 0;
}

测试结果：

5、优先队列(堆)测试

5.1++i和i++运算符的测试

#include <iostream>

using std::cout;
using std::endl;

int main()
{
    int i = 8;
    int arr[] = { 1,2,3,4,5,6,7,8,9 };

    //cout << arr[i--] << endl;    //打印9  先使用后修改
    //cout << arr[i--] << endl;    //打印8

    cout << arr[--i] << endl;    //打印8    先修改后使用
    cout << arr[--i] << endl;    //打印7
    cout << endl;
    cout << i;    //此时i=6

    system("pause");
    return 0;
}

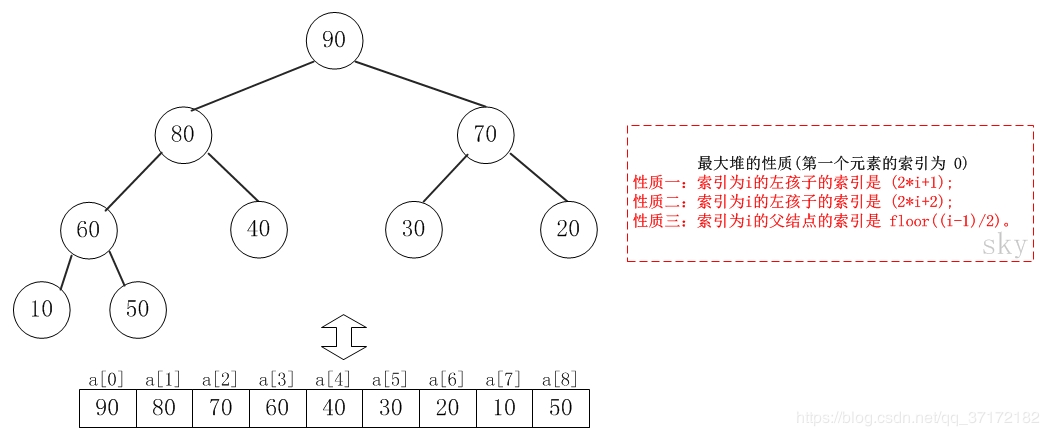
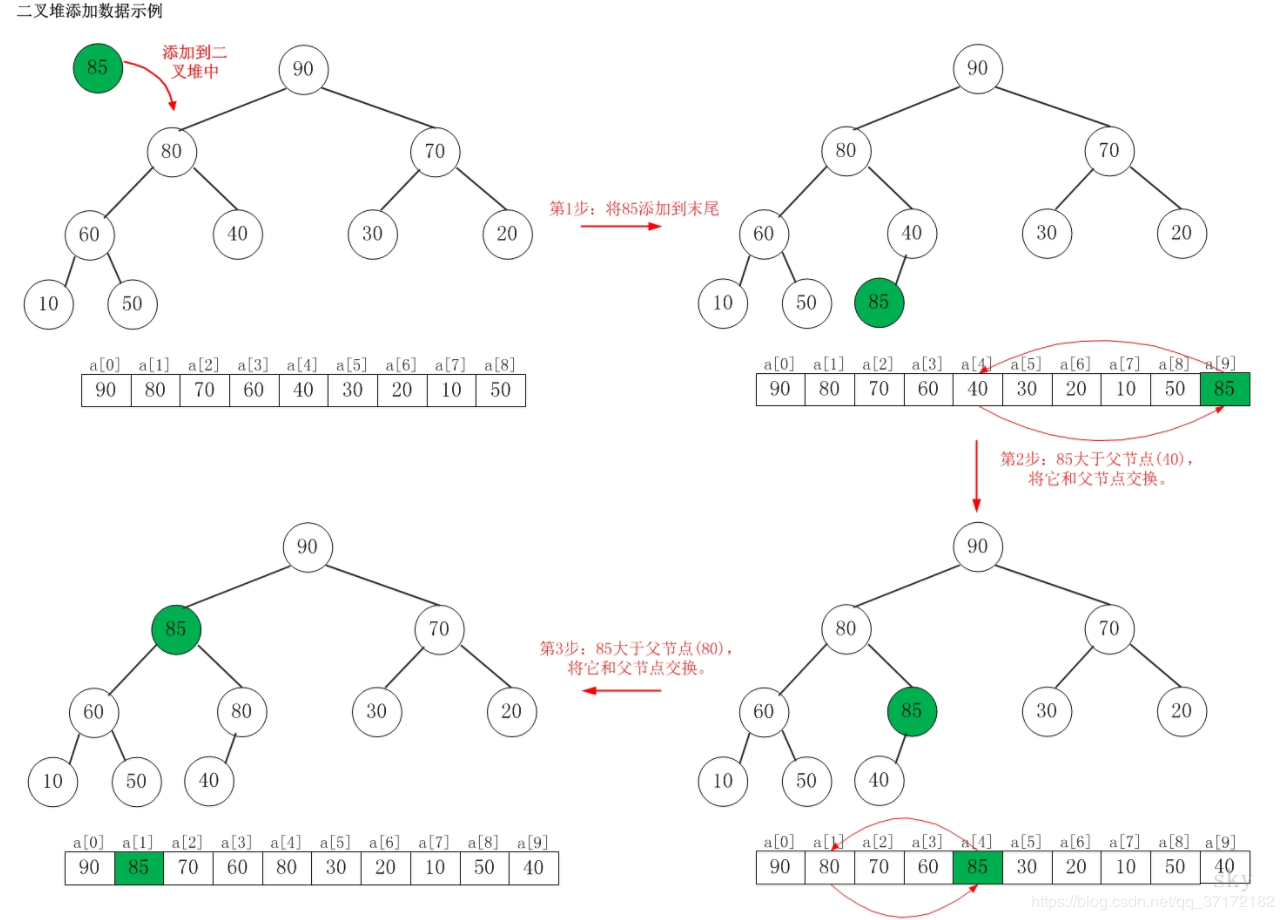
5.2优先队列上滤插入和下滤删除

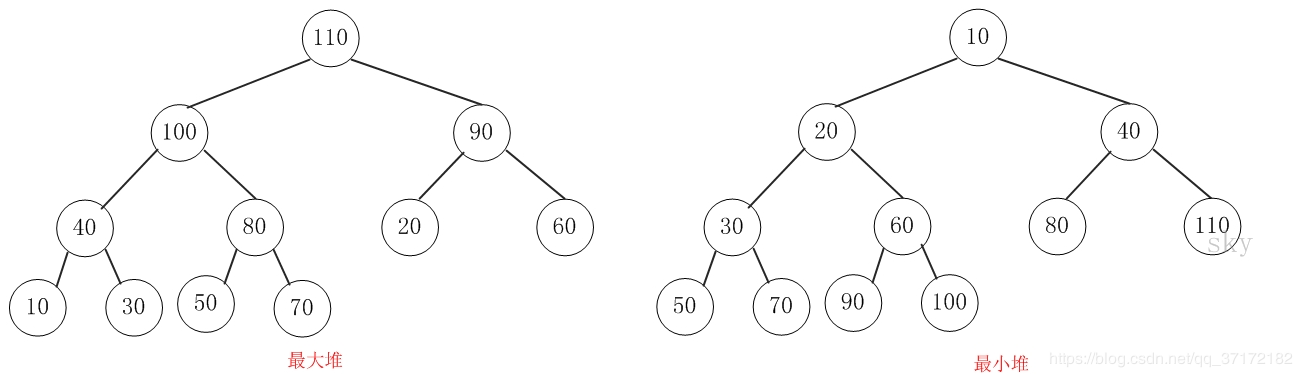
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；

最小堆：父结点的键值总是小于或等于任何一个子节点的键值；

 

 

 

 

/*最大堆的实现*/
#pragma once
#include <iostream>

using std::cout;
using std::endl;

template<class Type>
class Heap
{
private:
    Type* array;    //存放数据的堆矩阵
    int totalsize;  //可以存放的总的数据个数
    int currentsize;  //目前数据个数的索引
    void filterDown(int start, int end);    //删除数据使用下滤方法
    void filterUp(int start);              //插入数据使用上滤方法
public:
    Heap(int size = 30);  //默认堆大小为30
    ~Heap();
    int getIndex(Type data);  //获取data在堆内的索引
    int insert(Type data);
    int remove(Type data);
    void showHeap();  
};

template<class Type>
Heap<Type>::Heap(int size)
{
    array = new Type[totalsize];  //为堆(数组分配空间)
    totalsize = size;
    currentsize = 0;
}

template<class Type>
Heap<Type>::~Heap()
{
    totalsize = 0;
    currentsize = 0;
    delete[] array;
}

template <class Type>
int Heap<Type>::getIndex(Type data)
{
    for (int i = 0; i < currentsize; i++)
    {
        if (array[i] == data)
            return i;
    }
    return -1;  //没有在堆array中找到data则返回-1
}

template <class Type>
int Heap<Type>::insert(Type data)  //data即为要插入的数据
{
    if (currentsize == totalsize)  //判断堆是否已满
        return -1;
    array[currentsize] = data;    //将新插入的数据data先存入array数组的最后,注crrentsize是从0开始
    filterUp(currentsize);
    currentsize++;
    return 0;
}

template <class Type>
void Heap<Type>::filterUp(int start)
{
    int i = start;         //将传入的当前索引值传递给i
    int p = (i - 1) / 2;   //获取索引为i节点的父节点(根节点的索引从0开始)
    Type temp = array[i];  //将要插入的元素值赋给temp
    while (i > 0)
    {
        if (array[p] >= temp)  //由于实现的是最大堆,节点比左右字树值都是要大的
            break;
        else
        {
            array[i] = array[p];  //将父节点的值向下移动,移到当前新插入的元素的位置
            i = p;                //再沿着新插入节点的父节点为基础向上查找
            p = (i - 1) / 2;      //找到索引为i的节点的父节点
        }
    }
    array[i] = temp;              //执行完while循环之后找到的i就是我们要把元素插入的地方(索引)
}

template <class Type>
int Heap<Type>::remove(Type data)
{
    if (currentsize == 0)
        return -1;
    int index = getIndex(data);    //获取要删除元素的索引
    if (index == -1)               //如果没有在队列中找到data则getIndex()函数返回-1
        return -1;
    array[index] = array[--currentsize]; //将要删除的位置用最后一个元素替换(因为在插入函数里面插入元素后currentsize自加1,所以这里要加1)
    filterDown(index, currentsize - 1);  //将队列中倒数第二个元素的索引传入
    return 0;
}

template <class Type>
void Heap<Type>::filterDown(int start, int end)
{
    int i = start;
    int leftNode = 2 * i + 1;  //索引为i对应的左节点，右节点索引为2*i+2
    int temp = array[i];   //将最后一个元素(现在索引为要删除元素的索引)赋给一个临时变量
    while (leftNode <= end)
    {
        if (leftNode < end && array[leftNode] < array[leftNode + 1])   //leftNode+1则为右节点了
            leftNode = leftNode + 1;    //如果左节点的值小于右节点的值，则让左节点变成右节点
        if (temp >= array[leftNode])    //如果最后一个元素(此时索引为要删除的元素的索引)大于左右节点中最大的一个节点,则退出循环
            break;
        else
        {
            array[i] = array[leftNode];  //将要删除的元素下的左右节点中最大的一个节点替换掉最后一个元素
            i = leftNode;                //再以leftNode为主节点，向下比较
            leftNode = 2 * leftNode + 1;
        }
    }
    array[i] = temp;    //将队列中最后一个值赋给经过第112行变换后、索引为i的地方
}

template <class Type>
void Heap<Type>::showHeap()
{
    for (int i = 0; i < currentsize; i++)
        cout << array[i] << " " << endl;
}

/*最大堆测试*/
#include "PriorityQueue.h"

int main()
{
    {
        int arr[] = { 37,26,14,52,69,78,98,48,69,70 };
        int n = sizeof(arr) / sizeof(arr[0]);  //获取数组元素个数的新方法
        Heap<int>* heap = new Heap<int>(20);   //新建指向类模板的指针，不新建指针也是可以的如Heap<int> heap(20);
        for (int i = 0; i < n; i++)
        {
            heap->insert(arr[i]);
        }
        heap->showHeap();
        cout << endl;

        cout << "添加元素100" << endl;
        heap->insert(100);
        heap->showHeap();
        cout << endl;

        cout << "删除元素78" << endl;
        heap->remove(78);
        heap->showHeap();
    }

    system("pause");
    return 0;
}

运行结果：

参考博客：https://blog.csdn.net/qq_37172182/article/details/88978808 

5.3 C语言实现最小堆和堆排序

插入优先队列(堆)中的流程图：

 

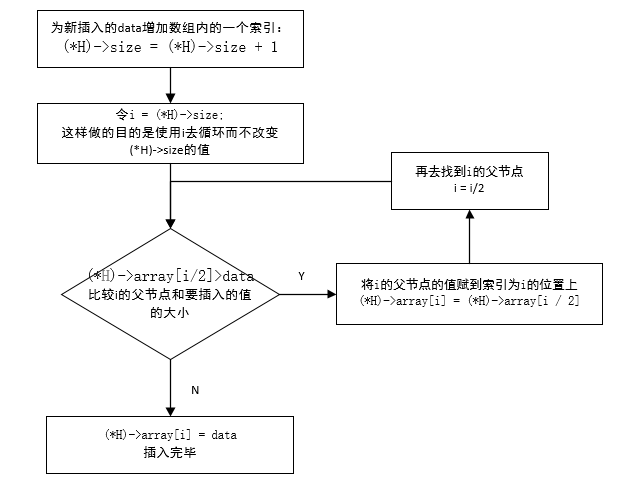
 删除写了注释，就没有画流程图。。。脑补原因吧~~哈哈

#pragma once
/*c语言实现优先队列(堆)*/
#include <iostream>
using std::cout;
using std::endl;

typedef int Type;
#define Mindata (-32767)

struct PriorQueue
{
    int size;  //堆当前元素数目
    int capacity;  //堆可容纳最大元素数
    Type* array;
};

PriorQueue* initQueue(int maxElements);  //优先队列(堆)初始化,返回值为一个指向结构的指针
bool isFull(PriorQueue* H);
bool isEmpty(PriorQueue* H);
void insert(PriorQueue** H, Type data);
Type deleteMinC(PriorQueue** H);
Type findMin(PriorQueue* H);
void destroy(PriorQueue** H);
void makeEmpty(PriorQueue** H);

/*C语言实现最小堆*/

#include "PriorityQueueC.h"

/*C语言实现有限队列初始化*/
PriorQueue* initQueue(int maxElements)
{
    PriorQueue* H = new PriorQueue;          //为结构分配空间
    H->array = new Type[maxElements + 1];    //为结构中的优先队列(实际上是一个数组)分配空间,由于数组索引从0开始,而最开始的索引0是不用的,故要加1才够maxElements数目
    H->size = 0;
    H->capacity = maxElements;
    H->array[0] = Mindata;                        //初始化优先队列中第一个元素为-32767
    return H;
}

bool isFull(PriorQueue* H)
{
    if (H->size == H->capacity)
        return true;
    else
        return false;
}
bool isEmpty(PriorQueue* H)
{
    if (H->size == 0)
        return true;
    else
        return false;
}

/*
01)优先队列(堆插入元素)
02)要向队列中插入data，要首先将其插入到数组的新开辟的位置上，数组新开辟的位置索引是(H->size)+1
03)由于根节点在数组内的索引是1，即第一个元素的索引为1；(索引为0的位置在初始化的时候已被占用)
   所以索引为i的父节点索引为i/2,左子节点索引为2*i,右子节点索引为2*i+1
04)首先为新插入的数分配一个数组索引i，然后比较i的父节点和索引为i的值的大小;若小于父节点则上去，否则不上去
*/
void insert(PriorQueue** H, Type data)
{
    if (isFull(*H))
    {
        cout << "优先队列(堆)已满！" << endl;
        return;
    }
    (*H)->size = (*H)->size + 1;  //为要插入的数字新开辟一个空间(数组内索引加1) (*H)->size就类似于一个int型变量
    int i;
    for (i = (*H)->size; (*H)->array[i / 2] > data; i = i / 2)
        (*H)->array[i] = (*H)->array[i / 2];    //如果父节点的值大于要插入的值，则将父节点的值插入到最后一个节点处(第一次循环)
    (*H)->array[i] = data;                      //为data找到一个合适的节点i
}

/*
01)删除元素(堆排序)
02)不断的去找一个节点i来存放堆内最后一个值,该节点i的特征是：堆内最后一个值比i的左右节点处的值都小;
   所以要先找出来节点i的左右节点中较小的那一个，然后再和堆内最后一个值比较；
03)要判断堆中元素数目为奇数还是偶数，因为如果堆内元素数为偶数，则有一个节点不存在右节点;
   判断方法为：if (child != (*H)->size && (*H)->array[child] > (*H)->array[child + 1])
   (01)如果(*H)->size为奇数，则child != (*H)->size恒成立（因为child=2*i）;此时任何一个节点都存在左右节点;
   (02)如果(*H)->size为偶数，则当child=(*H)->size的时候，不再执行后面的判断，因此不会报错。
*/
Type deleteMinC(PriorQueue** H)
{
    if (isEmpty(*H))
    {
        cout << "优先队列(堆)已空！" << endl;
        return (*H)->array[0];                    //不能只写一个return,是会报错的；返回默认的元素就好了
    }
    int i, child;
    Type lastData = (*H)->array[(*H)->size];
    Type minData = (*H)->array[1];                //先将最小的值保存起来,以免后面被破坏
    (*H)->size = (*H)->size - 1;                  //由于是要删除根节点的元素,所以堆内元素数是要减1的
    for (i = 1; i * 2 <= (*H)->size; i = child)   //从根节点开始,比较节点i的左右节点的大小，将较小的放入i的位置处
    {
        child = 2 * i;                            //节点i的左子节点
        if (child != (*H)->size && (*H)->array[child] > (*H)->array[child + 1])
            child++;                             //如果左子节点的值大于右子节点的值,则让child变成右子节点
        if ((*H)->array[child] < lastData)
            (*H)->array[i] = (*H)->array[child]; //如果节点i左右节点中较小的那一个比最后一个还要小,则让节点i处放左右节点中较小的那一个值
        else
            break;                               //否则,结束循环，即找到了存放lastData的节点i
    }
    (*H)->array[i] = lastData;
    return minData;
}

Type findMin(PriorQueue* H)
{
    if (isEmpty(H))
    {
        cout << "优先队列(堆)已空！" << endl;
        return 0;
    }
    else
        return H->array[1];
}

void makeEmpty(PriorQueue** H)
{
    (*H)->size = 0;
}

void destroy(PriorQueue** H)
{
    delete[](*H)->array;
    delete (*H);
    cout << "释放空间完毕" << endl;
}

/*C语言实现最小堆测试*/
#include "PriorityQueueC.h"

int main()
{
    PriorQueue* Queue;
    Queue = initQueue(10);
    int ar[] = { 32, 21, 16, 24, 31, 19, 68, 65, 26, 13 };
    cout << "输入的元素为：" << endl;
    for(int i = 0; i < 10; i++)
        cout << ar[i] << ", ";
    cout << endl;

    cout << "将数组内元素插入到优先队列(堆)中：" << endl;
    for (int i = 0; i < 10; i++)
        insert(&Queue, ar[i]);
    for(int i=1;i<11;i++)
        cout << Queue->array[i] << ", ";
    cout << endl;

    cout << "将优先队列(堆)中的元素进行堆排序：" << endl;
    for (int i = 0; i < 10; i++)
        cout << deleteMinC(&Queue) << ", ";
    cout << endl;

    destroy(&Queue);    //释放空间

    system("pause");
    return 0;
}

运行结果：

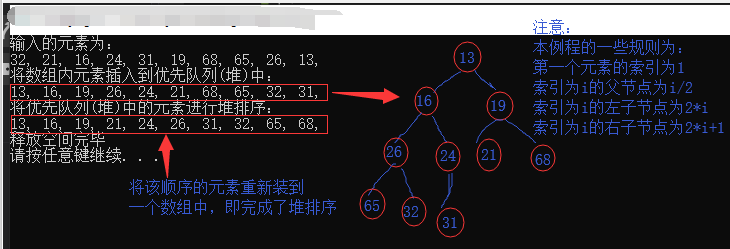
2019.10.04 下午

于 杭电 二教

6、队列

队列也是一种线性表，只不过它是操作受限的线性表，只能在两端操作，先进先出（First In First Out，FIFO）。进的一端称为队尾（rear），出的一端称为队头（front）。队列可以用顺序存储，也可以用链式存储。

(1) 队列结构体定义;

(2) 循环队列出队入队图解

1）开始时为空队，Q.front=Q.rear，如图所示：

 2）元素a1进队，放入尾指针Q.rear（整型下标）的位置，Q.rear后移一位，如图所示：

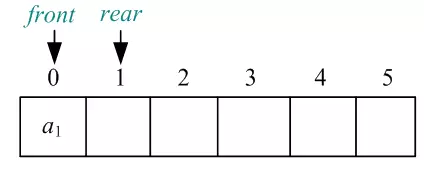
 03）元素a2进队，放入尾指针Q.rear（整型下标）的位置，Q.rear后移一位，如图所示：

 04）元素a3，a4，a5分别按顺序进队，尾指针Q.rear依次后移，如图所示：

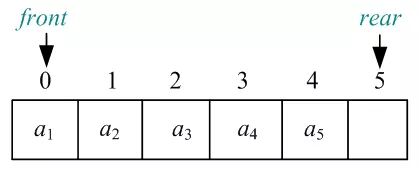
05）元素a1出队，头指针Q.front（整型下标）后移一位，如图所示：

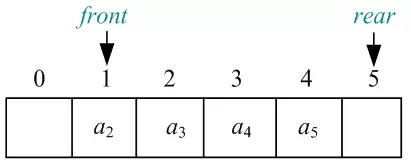
 06）元素a2出队，头指针Q.front（整型下标）后移一位，如图所示：

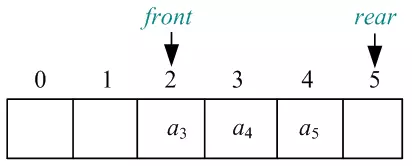
 07）元素a6进队，放入尾指针rear（整型下标）的位置，rear后移一位，如图所示：

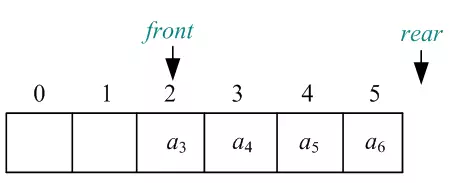
 素a6进队之后，尾指针Q.rear要后移一个位置，此时已经超过了数组的下标，即Q.rear+1=Maxsize（最大空间数6），那么如果前面有空闲，Q.rear可以转向前面0的位置，如图所示：

 08）元素a7进队，放入尾指针Q.rear（整型下标）的位置，Q.rear后移一位，如图所示：

 09）元素a8进队，放入尾指针Q.rear（整型下标）的位置，Q.rear后移一位，如图所示：

 10）这时候虽然队列空间存满了，但是出现了一个大问题，队满时Q.front=Q.rear，这和队空的条件一模一样，无法区分队空还是队满，如何解决呢？有两种办法：一是设置一个标志，标记队空和队满；另一种办法是浪费一个空间，当尾指针Q.rear的下一个位置Q.front是时，就认为是队满。如图所示：

                         此时认为队列已满（浪费了一个空间）

(3) 临界状态下，front和rear的取值方式

循环队列无论入队还是出队，出队或入队之后，队尾、队头加1后都要取模运算，例如入队后队尾后移一位：Q.rear =(Q.rear+1)%Maxsize。

为什么要使用Maxsize对（rear+1）取余呢？

主要是为了处理临界状态，即Q.rear向后移动一个位置Q.rear+1后，很有可能超出了数组的下标，这时它的下一个位置其实是0，如果将一维数组画成环形图，如图所示：

 

上图中最大空间Maxsize，当Q.rear=Maxsize-1时，(Q.rear+1)%Maxsize=0，而且Q.front=0，正好满足队满的条件：(Q.rear+1) %Maxsize= Q.front，此时为队满（用第一种方法判定队满）

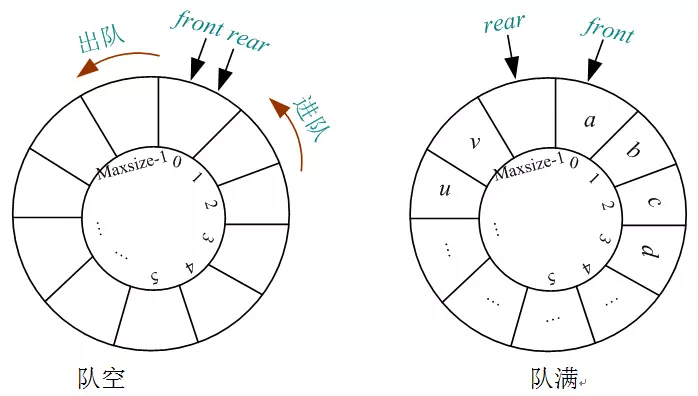
因此无论是front还是rear向后移动一个位置时，都要加1与最大空间Maxsize取模运算，处理临界问题。

(4) 总结

队空：Q.front=Q.rear; // Q.rear和Q.front指向同一个位置

队满： (Q.rear+1) %Maxsize=Q.front; // Q.rear向后移一位正好是Q.front

入队：

Q.base[Q.rear]=x; //将元素放入Q.rear所指空间，

Q.rear =( Q.rear+1) %Maxsize; // Q.rear向后移一位

出队：

e= Q.base[Q.front]; //用变量记录Q.front所指元素，

Q.front=(Q.front+1) %Maxsize // Q. front向后移一位

(5) 循环队列中存储的元素个数计算方式

因为队列是循环的，所以存在两种情况：

1) Q.rear>= Q.front，如下图所示：

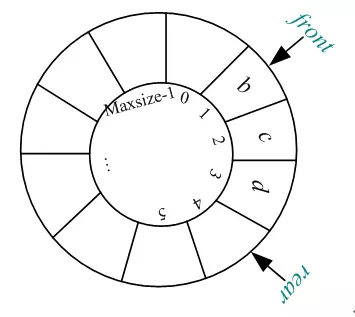
 这种情况队列中元素个数为：Q.rear-Q.front=4-1=3。

2) Q.rear< Q.front，如下图所示：

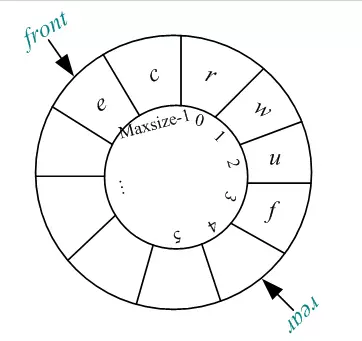
此时，Q.rear=4，Q.front=Maxsize-2，Q.rear-Q.front=6-Maxsize。但是我们可以看到循环队列中的元素实际上为6个，那怎么办呢？当两者之差为负数时，可以将差值+Maxsize计算元素个数，即：Q.rear-Q.front+Maxsize=6-Maxsize+Maxsize =6，元素个数为6。

那么在计算元素个数时，可以分两种情况判断：

Q.rear>= Q.front：元素个数为Q.rear-Q.front；

Q.rear<Q.front：元素个数为Q.rear-Q.front+ Maxsize；

也可以采用取模的方法把两种情况统一为一个语句：

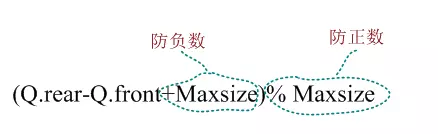
队列中元素个数：(Q.rear-Q.front+Maxsize)% Maxsize

当Q.rear-Q.front为负数时，加上Maxsize再取余正好是元素个数，如(-2+6)%6=4；当Q.rear-Q.front为正数时，加上Maxsize超过了最大空间数，取余后正好是元素个数，如(3+6)%6=3。

(6)、调试

#pragma once

#include <iostream>

using std::cout;
using std::endl;
using std::cin;

template <class Type>
class Queue
{
private:
    Type* queue;
    int rear;
    int front;
    int size;
public:
    explicit Queue(int totalsize = 30);  //队列大小默认为30
    ~Queue();
    bool isEmpty();
    bool isFull();
    void enqueue(Type data);
    void dequeue(Type & data);   //data对应于主函数中的实参,用于显示出队的元素
    Type getFront();             //取队首元素
    int queueLength();          //队列中元素个数
    /*void show();*/
};

/*队列初始化*/
template <class Type>
Queue<Type>::Queue(int totalsize)
{
    queue = new Type[totalsize];
    size = totalsize;
    front = 0;
    rear = 0;
}

/*析构函数*/
template <class Type>
Queue<Type>::~Queue()
{
    delete[] queue;
    size = rear = front = 0;
}

/*判断队列是否为空*/
template <class Type>
bool Queue<Type>::isEmpty()
{
    if (front == rear)
        return true;   //如果为空，则返回true
    else
        return false;
}

/*判断队列是否已满*/
template <class Type>
bool Queue<Type>::isFull()
{
    if (front == (rear+1)%size)
        return true;   //如果已满，则返回true
    else
        return false;
}

/*入队*/
template <class Type>
void Queue<Type>::enqueue(Type data)
{
    if (isFull())
    {
        cout << "The queue is full!" << endl;
        return;
    }
    queue[rear] = data;         //元素入队
    rear = (rear + 1) % size;   //队为加1,为防止溢出.rear加1后对size取余
}

/*
01)出队
02)有缺陷：队列中最后一个元素不会出队
*/
template <class Type>
void Queue<Type>::dequeue(Type & data)
{
    if (isEmpty())
    {
        cout << "The queue is empty!" << endl;
        return;
    }
    data = queue[front];          //由于形参是引用,所以形参的改变也会影响到实参,这里是要引用的目的是便于显示
    front = (front + 1) % size;   //将front加1，为防止溢出.front加1后对size取余
}

/*取队首元素*/
template <class Type>
Type Queue<Type>::getFront()
{
    if (isEmpty())
        return 0;
    else
        return queue[front];  //返回队首元素
}

/*返回队列中元素个数*/
template <class Type>
int Queue<Type>::queueLength()
{
    return (((rear - front) + size) % size);
}

//template <class Type>
//void Queue<Type>::show()
//{
//    int n = queueLength();
//    for (int i = 0; i < n; i++)
//    {
//        cout << queue[i];
//    }
//}

#include "queue.h"

int main()
{
    int x;
    int temp;
    int size = 6;
    Queue<int>* queue = new Queue<int>(size);
    cout << "请输入一个整数，按字母q结束：";
    cin >> x;
    while (x != 0)
    {
        queue->enqueue(x);
        cout << "请输入一个整数，按字母q结束：";
        cin >> x;
    }
    cout << "队中元素个数为：" << queue->queueLength() << endl;
    for (int i = 0; i <= queue->queueLength(); i++)
    {
        queue->dequeue(temp);
        cout << "出队的元素是：" << temp << endl;
    }

    system("pause");
    return 0;
}

运行结果：

 

 是for循环出了问题，不能使用函数queue->queueLength()写在for循环里边

#include "queue.h"

int main()
{
    int x;
    int temp;
    int size = 6;
    Queue<int>* queue = new Queue<int>(size);
    cout << "请输入一个整数，按字母q结束：";
    cin >> x;
    while (x != 0)
    {
        queue->enqueue(x);
        cout << "请输入一个整数，按字母q结束：";
        cin >> x;
    }
    cout << "队中元素个数为：" << queue->queueLength() << endl;
    int n = queue->queueLength();
    for (int i = 0; i <= n; i++)
    {
        queue->dequeue(temp);
        cout << "出队的元素是：" << temp << endl;
    }
    /*queue->dequeue(temp);
    cout << "出队的元素是：" << temp << endl;
    queue->dequeue(temp);
    cout << "出队的元素是：" << temp << endl;
    queue->dequeue(temp);
    cout << "出队的元素是：" << temp << endl;
    queue->dequeue(temp);
    cout << "出队的元素是：" << temp << endl;
    queue->dequeue(temp);
    cout << "出队的元素是：" << temp << endl;
    queue->dequeue(temp);
    cout << "出队的元素是：" << temp << endl;

    queue->dequeue(temp);
    cout << "出队的元素是：" << temp << endl;*/

    system("pause");
    return 0;
}

（7）C++中的queue类

用法：

queue<int> Q;              　　　　//定义一个int型队列
Q.empty();                    　　     //返回队列是否为空
Q.size();                                  //返回当前队列长度
Q.front();                                //返回当前队列的第一个元素
Q.back();                                //返回当前队列的最后一个元素
Q.push();                 　　  　 　//在队列后面插入一个元素, 比如插入数字5: Q.push(5)
Q.pop();                                //从当前队列里,移出第一个元素

#include <iostream>
#include <queue>

using namespace std;
int main()
{
       queue<int> Q;
       cout<<"queue empty?  "<<Q.empty()<<endl;

       for(int i=0;i<5;i++)
       {
              Q.push(i);        //进队列
       }

       cout<<"queue empty?  "<<Q.empty()<<endl;
       cout<<"queue size:   "<<Q.size()<<endl;
       cout<<endl;

       for(int i=0;i<5;i++)
       { 
              cout<<"queue front:  "<<Q.front()<<endl;    
              Q.pop();                //出队列
       }

       return 0;
}

参考博客：https://www.cnblogs.com/lifexy/p/8884048.html

7、栈

（1）自己的方法实现

栈的最基本操作是后进先出，其实前边已经实现了这种功能，只是函数名字不是push()和pop()，比如链表的初始化和创建

#pragma once
/*栈的列表实现*/
#include <iostream>

using std::cout;
using std::endl;

typedef int Type;
struct Stack
{
    Type data;
    Stack* next;
};


void initStack(Stack** head);
bool isEmpty(Stack** head);
void push(Stack** head, Type data);    //该data是传入到栈的数据,不可以省略
void pop(Stack** head, Type & data);   //该data是传入到主函数用于显示,可以省略
 

#include "stack.h"

void initStack(Stack** head)
{
    if ((*head) == NULL)
        return;
    (*head) = new Stack;
    (*head)->next = NULL;
    (*head)->data = 0;
}

bool isEmpty(Stack** head)
{
    return (*head)->next == NULL ? true : false;
}

/*利用链表的头插法实现入栈操作*/
void push(Stack** head, Type data)
{
    Stack* node;
    node = new Stack;
    node->next = (*head)->next;
    node->data = data;
    (*head)->next = node;
}

/*传入的是头结点*/
void pop(Stack** head, Type & data)
{
    Stack* node;
    if (isEmpty(&(*head)))
    {
        cout << "栈已空！" << endl;
        return;
    }
    node = (*head)->next;       //node为头结点的下一个节点,即要输出的数据的节点
    data = node->data;
    (*head)->next = node->next;
    delete node;
}

/*栈测试代码*/
#include "stack.h"

Type data;

int main()
{
    Stack* stack;
    initStack(&stack);
    cout << "入栈的数据为：" << 1 << endl;
    push(&stack, 1);
    cout << "入栈的数据为：" << 2 << endl;
    push(&stack, 2);
    cout << "入栈的数据为：" << 3 << endl;
    push(&stack, 3);

    cout << endl;

    pop(&stack, data);
    cout << "出栈的数据为：" << data << endl;
    pop(&stack, data);
    cout << "出栈的数据为：" << data << endl;
    pop(&stack, data);
    cout << "出栈的数据为：" << data << endl;

    pop(&stack, data);

    system("pause");
    return 0;
}

运行结果：

 2019.10.02 晚 

于杭电二教南336

（2）使用C++库函数stack实现

C++中的stack为程序员实现了堆栈的全部功能，也就是说实现了一个先进后出(FILO)的数据结构。

#include <iostream>
#include <stack>

using namespace std;

int main()
{
    stack<int> s;
    s.push(1);    //入栈
    s.push(2);
    s.push(3);
    s.push(4);
    s.push(5);

    cout << "栈中元素个数为：" << s.size() << endl;

    while (!s.empty())           //如果栈中元素为空，empty()则返回0
    {
        cout << s.top() << " ";  //top()返回栈顶元素
        s.pop();                 //将当前栈顶元素出栈
    }
    cout << endl;
    system("pause");
    return 0;
}

运行结果：

8、快速排序

快速排序算法是一种基于交换的高效的排序算法，它采用了分治法的思想：

1、从数列中取出一个数作为基准数（枢轴，pivot）。 

2、将数组进行划分(partition)，将比基准数大的元素都移至枢轴右边，将小于等于基准数的元素都移至枢轴左边。

3、再对左右的子区间重复第二步的划分操作，直至每个子区间只有一个元素。

快排最重要的一步就是划分了。划分的过程用通俗的语言讲就是“挖坑”和“填坑”。

实现方法一：

算法流程如下所示：

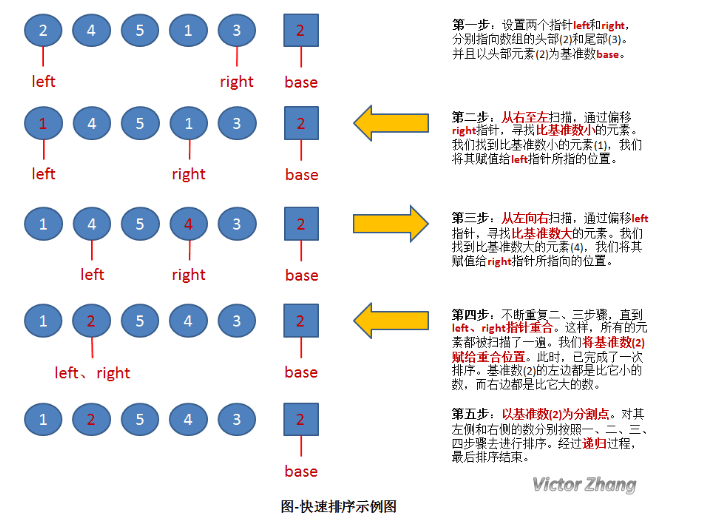
参考博客：https://www.cnblogs.com/miracleswgm/p/9199124.html

/*快速排序*/
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <time.h>

using namespace std;

void QuickSort(int array[], int start, int last)
{
    int i = start;
    int j = last;
    int temp = array[i];
    /*下面的循环直到i=j结束，即找到中心，再以i为中心，分别对左右分别进行快速排序*/
    if (i < j)
    {
        while (i < j)
        {
            //
            while (i < j &&  array[j] >= temp)  //从右向左扫描,找到比temp小的值,并退出循环
                j--;                            //通过自减j,找到第一个比temp小的值的位置j
            if (i < j)
            {
                array[i] = array[j];            //将第一个比temp小的值赋在数组中i的位置上
                i++;                            //赋值后将左边指针自加1
            }

            while (i < j && temp > array[i])    //从左向右扫描,找到比temp大的值,并退出循环
                i++;                            //通过自增i,找到第一个比temp大的值的位置i
            if (i < j)
            {
                array[j] = array[i];            //将第一个比temp大的值赋在数组中j的位置
                j--;                            //赋值后将右边指针自减1
            }

        }
        //把基准数放到中间i位置
        array[i] = temp;
        //递归方法，以i为中心，分左右进行快速排序
        QuickSort(array, start, i - 1);  //对从start到i-1的数字进行快速排序
        QuickSort(array, i + 1, last);   //对从i+1到last的数字进行快速排序
    }
}

void PrintArray(int array[], int len)
{
    for (int i = 0; i < len; i++)
    {
        cout << array[i] << " ";
    }
    cout << endl;
}

int main(void)
{
    const int NUM = 10;
    int array[NUM] = { 0 };
    srand((unsigned int)time(nullptr));
    for (int i = 0; i < NUM; i++)
    {
        array[i] = rand() % 100 + 1;
    }
    cout << "排序前：" << endl;
    PrintArray(array, NUM);
    cout << "排序后：" << endl;
    QuickSort(array, 0, NUM - 1);
    PrintArray(array, NUM);

    system("pause");
    return 0;
}

/*递归*/
/*
void recurs(argumentlist)
{
    statment1;
    if (test)
        recurs(arguments);
    statment2;
}
01)通常是将递归调用放在if语句中，例如上述递归调用recurs(arguments);放在了if语句中
02)当test为true时,每个recurs()都将执行statment1,然后再调用recurs(),而不会执行statment2；
03)当test为false时,当前调用执行statment2,程序将控制权返回给调用它的recurs(),而该recurs()将执行它的statment2部分,然后结束
   并将控制权返回给前一个调用，以此类推；
04)因此，如果recurs()执行了5次递归调用，则statment1将按照函数调用顺序执行5次，statment2将按照与函数调用相反的顺序执行5次
*/

执行结果：

快速排序实现方法二：

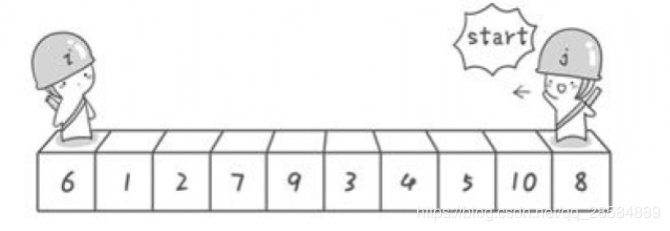
假如要对6  1  2 7  9  3  4  5 10  8 这十个数字进行从小到大排序：

(1)选第一个数字6为基准数，分别从左边探测第一个比6大的数，从右边探测第一个比6小的数，如果找到了，则交换二者，注意如果选左边第一个数作为基准数，则此时要先  从右边开始扫描；若选右边第一个数作为基准数，则先从左边开始扫描；为方便，令i指向第一个位置，j指向最后一个位置，刚开始的时候让i指向序列的最左边（即i=1），指向数字6。让j指向序列的最右边（即j=10），指向数字8；

 

 

(2)先让j向左移动，即j--，直到找到第一个比6小的位置，即5停下来；然后让i向右移动，即i++，直到找到第一个比6大的位置，即7停下来；交换i和j位置处的值，即交换5和7；

 

(3)接下来开始j继续向左挪动（再友情提醒，每次必须是哨兵j先出发），直到在4的位置停下来，i也继续向右挪动的，他发现了9（比基准数6要大，满足要求）之后停了下来。交换i和j位置处的值，即交换9和4；

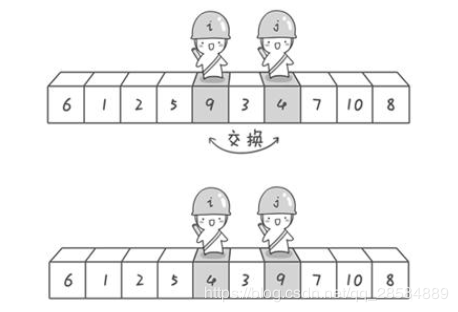
(4)j继续先向右移动(j--)，在3的位置停下来，假如i遇到比6大的值，一定是会停下来的，如果没有遇到，则i和j相遇，此时是要交换首位置和此时j所处的位置的值，满足了6的左边全是比6小的值 和 6的右边全是比6大的值的特点；这也许是必须先从右边移动的原因了吧，关键是在于相遇时的值的确定的问题，即假如先从右边开始移动的话，那么相遇处的值一定是会比基准值小的，在相遇时，要交换相遇位置的值和首位值的值，如下所示:

 

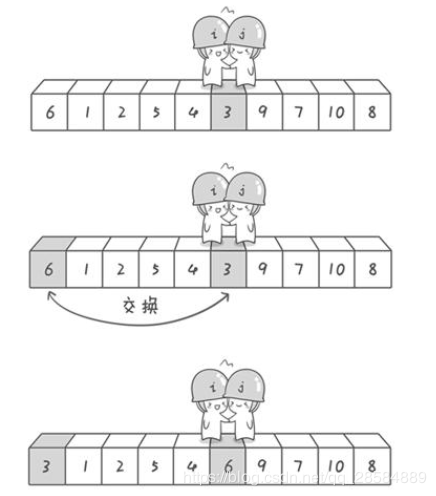
     到此第一轮“探测”真正结束。此时以基准数6为分界点，6左边的数都小于等于6，6右边的数都大于等于6。回顾一下刚才的过程，其实哨兵j的使命就是要找小于基准数的数，而哨兵i的使命就是要找大于基准数的数，直到i和j碰头为止。

此时我们已经将原来的序列，以6为分界点拆分成了两个序列，左边的序列是“3  1 2  5  4”，右边的序列是“9  7  10  8”。接下来还需要分别处理这两个序列，使用递归即可。

霸气的图描述算法全过程：

参考博客：https://blog.csdn.net/qq_28584889/article/details/88136498

实现代码：

/*方法二实现快速排序*/
void QuickSort(int arr[], int left, int right)
{
    int i = left;
    int j = right;
    int base = arr[i];  //以最左边的值为基准值
    if (i > j)
        return;
    while (i < j)
    {
        while (base <= arr[j] && i<j)     //找到比temp小的值(此时为从小到大排序,如果是要从大到小排序,则此处找比temp大的值)
            j--;
        while (base >= arr[i] && i<j)     //找到比temp大的值(此时为从小到大排序,如果是要从大到小排序,则此处找比temp小的值)
            i++;
        if (i < j)
        {
            int temp = arr[i];     //交换位置i个位置j处的值
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    arr[left] = arr[i];           //将i和j相遇处的值放在首位置,因为是从右边开始探索比基准值小的值,所以i和j相遇处的值一定比6小
    arr[i] = base;                //将基准值放在"中间位置",该"中间位置"的左边全是比base小的值,右边全是比base大的值
    QuickSort(arr, left, i - 1); 
    QuickSort(arr, i + 1, right);
}

void PrintArray(int array[], int len)
{
    for (int i = 0; i < len; i++)
    {
        cout << array[i] << " ";
    }
    cout << endl;
}

int main(void)
{
    const int NUM = 10;
    int array[NUM] = { 0 };
    srand((unsigned int)time(nullptr));
    for (int i = 0; i < NUM; i++)
    {
        array[i] = rand() % 100 + 1;
    }
    cout << "排序前：" << endl;
    PrintArray(array, NUM);
    cout << "排序后：" << endl;
    QuickSort(array, 0, NUM - 1);
    PrintArray(array, NUM);

    system("pause");
    return 0;
}

/*递归*/
/*
void recurs(argumentlist)
{
    statment1;
    if (test)
        recurs(arguments);
    statment2;
}
01)通常是将递归调用放在if语句中，例如上述递归调用recurs(arguments);放在了if语句中
02)当test为true时,每个recurs()都将执行statment1,然后再调用recurs(),而不会执行statment2；
03)当test为false时,当前调用执行statment2,程序将控制权返回给调用它的recurs(),而该recurs()将执行它的statment2部分,然后结束
   并将控制权返回给前一个调用，以此类推；
04)因此，如果recurs()执行了5次递归调用，则statment1将按照函数调用顺序执行5次，statment2将按照与函数调用相反的顺序执行5次
*/

运行结果：

 (3)使用快速排序算法找到数组中第k大的值(笔试题)

int QuickSort(vector<int> arr,int left,int right,int k)
{
    int i=left;
    int j=right;
    int base=arr[i];
    while(i<j)
    {
        while(base>=arr[j] && i<j)
            j--;
        while(base<=arr[i] && i<j)
            i++;
        if(i<j)
        {
            int temp=arr[i];
            arr[i]=arr[j];
            arr[j]=temp;
        }
    }
    arr[left]=arr[i];
    arr[i]=base;
    if(k == i+1)  //数组元素从0开始
        return arr[i];
    else if(k<i+1)      //说明第k大的元素在数组前半段
        return QuickSort(arr,left,i-1,k);
    else                //说明第k大元素在数组后半段
        return QuickSort(arr,i+1,right,k);
}

牛客网原题位置：https://www.nowcoder.com/practice/e016ad9b7f0b45048c58a9f27ba618bf 

 (4)快速排序是一种不稳定的排序方法的原因

 

9、冒泡排序

原理：

(1)两两比较相邻元素A(I)和A(I+1)(I=1,2,…N-1),如果A(I)>A(I+1),则交换A(I)和A(I+1)的位置；

(2)对剩下的N-1个元素，再两两进行比较，按同样规则交换它们的位置,经过N-2次比较,将次最大值交换到A(N-1)的位置;

(3)如法炮制,经过N-1趟的“冒泡处理”,每趟进行N-i次的比较,全部数列有序。

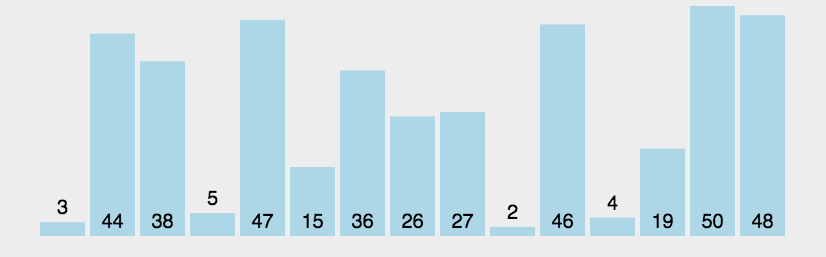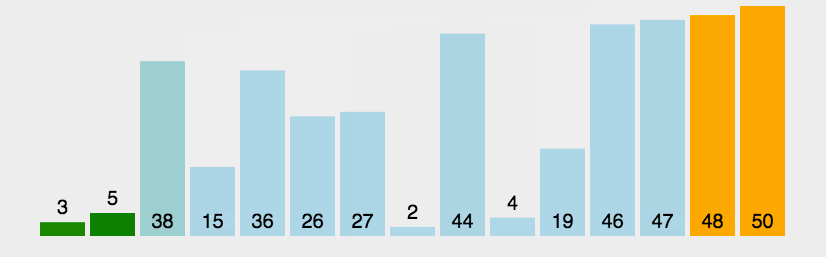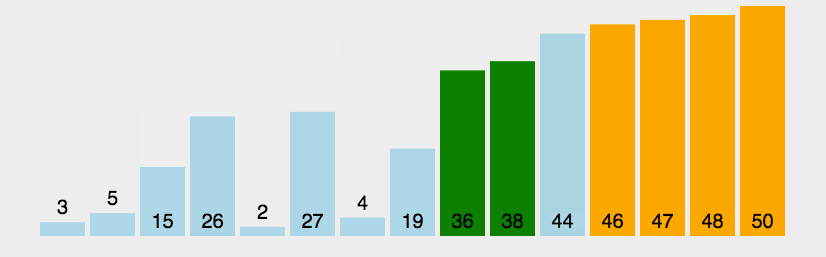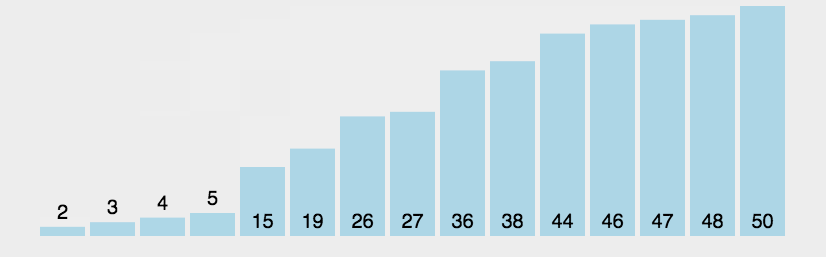
该图片地址：https://img-blog.csdnimg.cn/20190326182928474.gif （注：有的浏览器可能播放不了该图片中的动画）

代码（使用srand()和rand()自动生成数组）：

#include <iostream>
#include <time.h>    //for time()

using namespace std;


/*冒泡排序*/
void BubbleSort(int arr[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = 0; j < n - i - 1; j++)
        {
            if (arr[j] > arr[j + 1])        //如果前一个数比后一个数大,则交换二者的顺序;总的来说就是将大的数字后移
            {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

/*打印数组*/
void PrintArray(int arr[], int n)
{
    for (int i = 0; i < n; i++)
        cout << arr[i] << ",";
    cout << endl;
}

int main()
{
    const int NUM = 10;                    //NUM如果作为数组大小,必须为常量          
    int array[NUM];                      
    srand((unsigned int)time(nullptr));    //初始化随机生成函数
    for (int i = 0; i < NUM; i++)
    {
        array[i] = rand() % 100 + 1;       //随机生成1-100以内的数字
    }
    cout << "排序前: " << endl;
    PrintArray(array, NUM);
    cout << "排序后: " << endl;
    BubbleSort(array, NUM);
    PrintArray(array, NUM);

    system("pause");
    return 0;
}

(1)i=0即可完成将数组中最大值放到数组最后的位置，第一次循环n-1-0次

(2)i=1即可完成将数组中第二大值放到数组倒数第二的位置 ，第二次循环n-1-1次，由于在数组中n-2到n-1位置已经排序完成,故下一次循环n-1-2次即可

(3)i=1即可完成将数组中第三大值放到数组倒数第三的位置 ，第三次循环n-1-2次,由于在数组中n-3到n-1位置已经排序完成,故下一次循环n-1-3次即可

即第二次层循环中j结束条件为j< n - i -1

运行结果：

10、生成n位格雷码

在一组数的编码中，若任意两个相邻的代码只有一位二进制数不同， 则称这种编码为格雷码(Gray Code)

例如：

1位格雷码为：0  1
2位格雷码为：00 01 11 10
3位格雷码为：000 001 011 010 110 111 101 100

格雷码有如下规律：

• 除了1之外，其他所有位数的格雷码的个数都是2的n次方
• n=3的gray码其实就是对n=2的gray码首位添加0或1生成的，添加0后变成(000,001,011,010)，添加1后需要顺序反向就变成(110,111,101,100)，组合在一起就是(000,001,011,010,110,111,101,100)

#include <iostream>
#include <vector>
#include <string>

using std::endl;
using std::cout;
using std::cin;
using std::string;
using std::vector;

vector<string> getGray(int n)
{
    vector<string> gray;
    vector<string> lastGray;
    if (n == 1)
    {
        gray.push_back("0");
        gray.push_back("1");
        return gray;
    }
    lastGray = getGray(n - 1);
    /*在n-1位格雷码的前面加(顺序)0*/
    for (int i = 0; i < lastGray.size(); i++)
        gray.push_back("0" + lastGray[i]);
    /*在n-1为格雷码的前面(反序)加1*/
    for (int i = lastGray.size() - 1; i >= 0; i--)
        gray.push_back("1" + lastGray[i]);
    return gray;
}

int main()
{
    vector<string> gray;
    int n = 3;
    gray = getGray(n);
    cout << n << "位格雷码为：" << endl;
    for (int i = 0; i < gray.size(); i++)
        cout << gray[i] << " ";
    cout << endl;

    system("pause");
    return 0;
}

运行结果：

11、二叉树

1、基本概念以及初级实现和遍历方法

对于二叉树，有深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法；广度遍历即我们寻常所说的层次遍历。

以图片的方式呈现吧

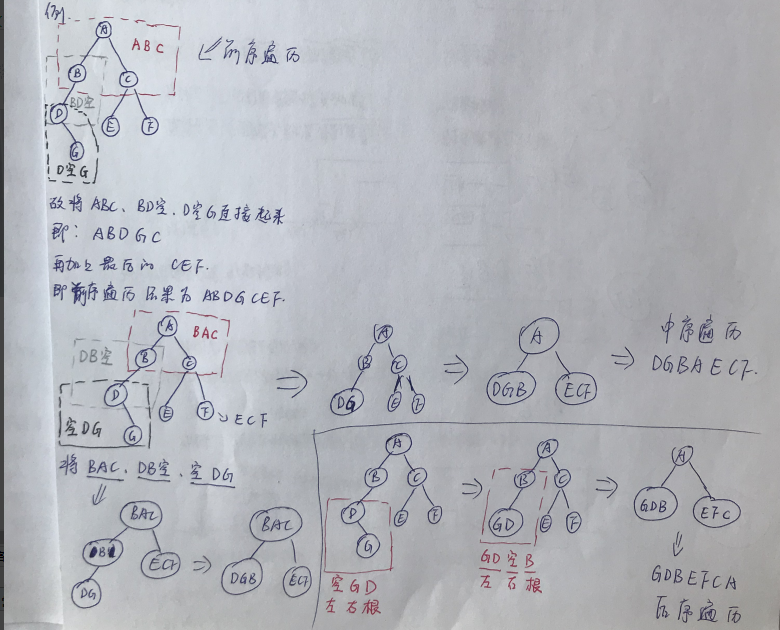
#include <iostream>

using namespace std;

struct treeNode
{
    char data;
    treeNode* LChild;
    treeNode* RChild;
};

//typedef struct treeNode* LPTREE;
#define LPTREE treeNode*

//指针一般用LP开头
LPTREE createNode(const char data)  //此处的LPTREE就是一个指针，如果传入的数据为'A',那么'A'就是const类型的,data如果不是const就会报错
{
    LPTREE newNode = (LPTREE)malloc(sizeof(treeNode));
    //LPTREE newNode = new treeNode;
    newNode->data = data;
    newNode->LChild = NULL;
    newNode->RChild = NULL;
    return newNode;
}

//插入数据
void insertNode(LPTREE parentNode, LPTREE LChild, LPTREE RChild)
{
    parentNode->LChild = LChild;
    parentNode->RChild = RChild;
}

//打印当前结点数据
void printCurNodeData(LPTREE curData)
{
    cout << curData->data << "\t";
}

//递归法遍历
//先序遍历：根左右
void preOrder(treeNode* root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        printCurNodeData(root);  //前序遍历先打印根节点  根
        preOrder(root->LChild);  //再打印根节点的左节点  左
        preOrder(root->RChild);  //再打印根节点的右节点  右
    }
}

//中序遍历：左根右
void midOrder(LPTREE root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        midOrder(root->LChild);  //左
        printCurNodeData(root);  //根
        midOrder(root->RChild);  //右
    }
}

//后序遍历：左右根
void lastOrder(LPTREE root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        lastOrder(root->LChild);  //左
        lastOrder(root->RChild);  //右
        printCurNodeData(root);   //根
    }
}

int main()
{
    LPTREE A = createNode('A');
    LPTREE B = createNode('B');
    LPTREE C = createNode('C');
    LPTREE D = createNode('D');
    LPTREE E = createNode('E');
    LPTREE F = createNode('F');
    LPTREE G = createNode('G');

    //很死板的创建二叉树方法
    insertNode(A, B, C);
    insertNode(B, D, NULL);
    insertNode(D, NULL, G);
    insertNode(C, E, F);

    cout << "先序遍历" << endl;
    preOrder(A);

    cout << "\n\n中序遍历\n";
    midOrder(A);

    cout << "\n\n后序遍历\n";
    lastOrder(A);

    system("pause");
    return 0;
}

原理：以三个结点为例

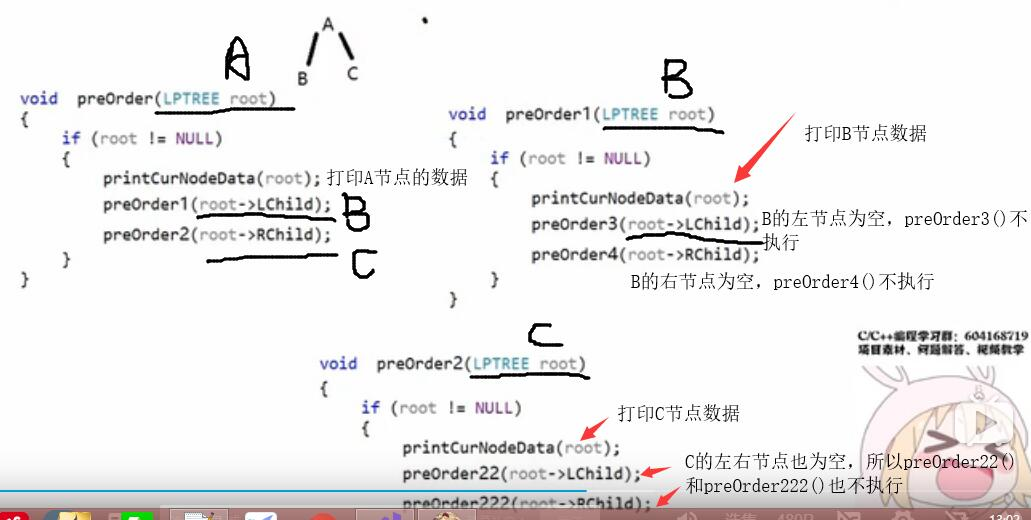
执行结果：

2、非递归方法实现三种遍历

(1)非递归方式前序遍历---使用栈数组

(2)非递归方式中序遍历---使用栈数组

(3)非递归方式后序遍历---使用栈数组

 

 

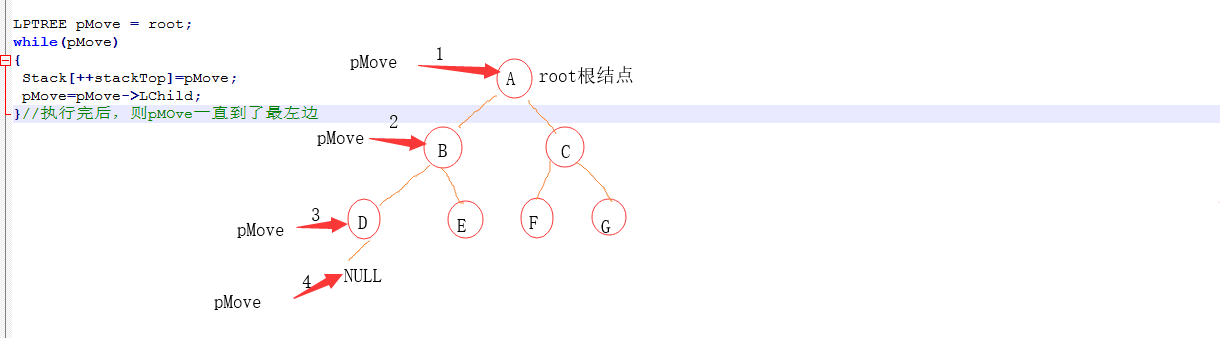
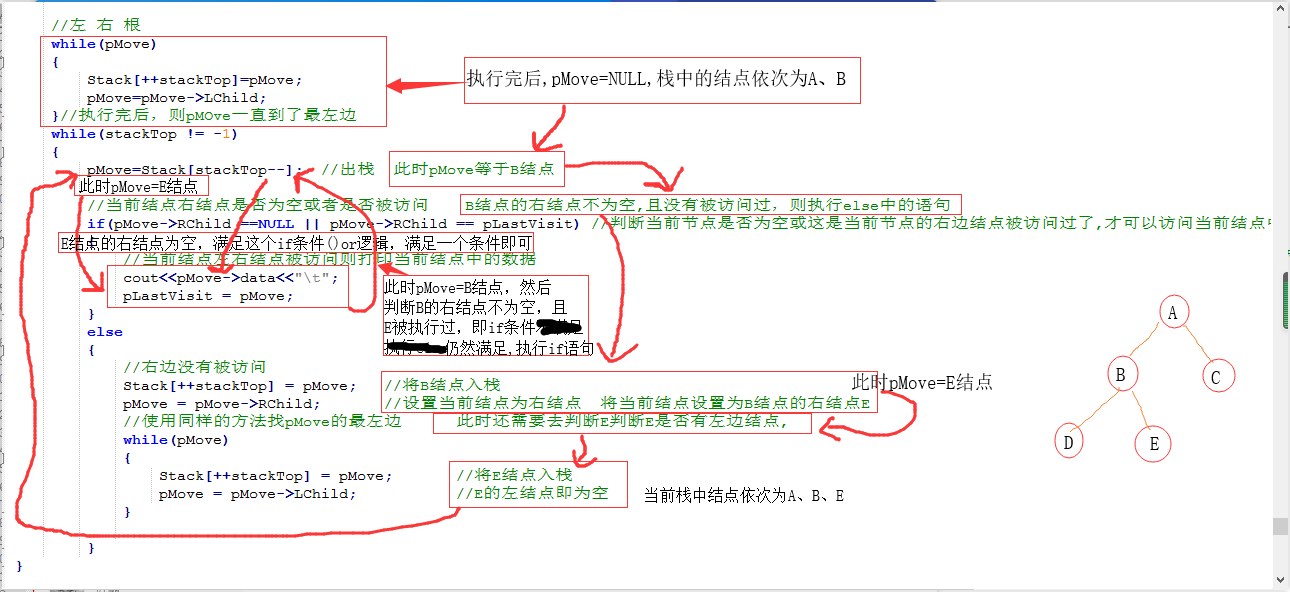
 非递归遍历代码实现：

#include <iostream>

using namespace std;

struct treeNode
{
    char data;
    treeNode* LChild;
    treeNode* RChild;
};

//typedef struct treeNode* LPTREE;
#define LPTREE treeNode*

//指针一般用LP开头
LPTREE createNode(const char data)  //此处的LPTREE就是一个指针，如果传入的数据为'A',那么'A'就是const类型的,data如果不是const就会报错
{
    LPTREE newNode = (LPTREE)malloc(sizeof(treeNode));
    //LPTREE newNode = new treeNode;
    newNode->data = data;
    newNode->LChild = NULL;
    newNode->RChild = NULL;
    return newNode;
}

//插入数据
void insertNode(LPTREE parentNode, LPTREE LChild, LPTREE RChild)
{
    parentNode->LChild = LChild;
    parentNode->RChild = RChild;
}

//打印当前结点数据
void printCurNodeData(LPTREE curData)
{
    cout << curData->data << "\t";
}

//递归法遍历
//先序遍历：根左右
void preOrder(treeNode* root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        printCurNodeData(root);  //前序遍历先打印根节点  根
        preOrder(root->LChild);  //再打印根节点的左节点  左
        preOrder(root->RChild);  //再打印根节点的右节点  右
    }
}

//中序遍历：左根右
void midOrder(LPTREE root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        midOrder(root->LChild);  //左
        printCurNodeData(root);  //根
        midOrder(root->RChild);  //右
    }
}

//后序遍历：左右根
void lastOrder(LPTREE root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        lastOrder(root->LChild);  //左
        lastOrder(root->RChild);  //右
        printCurNodeData(root);   //根
    }
}

//非递归方式前序遍历---使用栈数组
void preOderByStack(LPTREE root)
{
    if (root == NULL)
        return;
    //住准备栈
    LPTREE Stack[10];   //一般使用数组栈，很少再写一个栈实现
    int stackTop = -1;  //栈顶标记
    LPTREE pMove = root;  //从根节点开始打印

    //当栈里面还有路径可以退或者是当前结点pMOve不为空
    while (stackTop != -1 || pMove)
    {
        //根左右
        //下面的这个循环即可找到最左边的节点
        while (pMove)
        {
            //把走过的路径入栈+打印走过的结点
            cout << pMove->data << "\t";    //打印
            Stack[++stackTop] = pMove;  //入栈，一定是++stackTop,因为stackTop初始化为-1
            /*
               如果stackTop初始化为50，则入栈的时候写成stack[++stackTop-50] = pMove;即可
            */
            pMove = pMove->LChild;  //将当前pMove的左节点赋给pMove
        }
        //找到最左边的节点后便无路可走，那么此时出栈
        if (stackTop != -1)
        {
            pMove = Stack[stackTop];  //获取栈顶元素
            stackTop--;  //伪出栈
            pMove = pMove->RChild;    //将当前结点的右结点赋给pMove
        }
    }
}

//非递归方式中序遍历---使用栈数组
/*
01)定义一个指针移动到最左边，把走过的地方入栈
02)无路的时候，出栈，打印当前结点中的元素
03)出栈后，打印当前结点元素，判断当前结点是否存z右边结点，如果存在就去右边
*/
void midOrderByStack(LPTREE root)
{
    if (root == NULL)
        return;
    LPTREE Stack[10];
    int stackTop = -1;

    //定义移动指针，初始化指向根结点root
    LPTREE pMove = root;
    //当栈里面还有路径可以退或者是当前结点pMOve不为空
    while (stackTop != -1 || pMove)
    {
        //走到最左边，把走做的路径入栈
        while (pMove)
        {
            Stack[++stackTop] = pMove;  //将当前结点入栈(走过的结点入栈)
            pMove = pMove->LChild;      //将当前结点的右结点赋给当前结点
        }
        //当当前节点的左结点为空，即无路可走时执行下面代码
        if (stackTop != -1)
        {
            pMove = Stack[stackTop--];  //先将栈中最上面元素赋给pMove：pMove = Stack[stackTop]；然后stackTop--
            cout << pMove->data << "\t";    //打印当前结点根结点中的元素
            pMove = pMove->RChild;
        }
    }
}

//非递归方式后序遍历---使用栈数组
void lastOrderByStack(LPTREE root)
{
    if (root == NULL)
        return;
    LPTREE Stack[10];
    int stackTop = -1;

    //定义移动指针，初始化指向根结点root
    LPTREE pMove = root;

    LPTREE pLastVisit = NULL;  //最后一次访问的标记

    //左 右 根
    while (pMove)
    {
        Stack[++stackTop] = pMove;
        pMove = pMove->LChild;
    }//执行完后，则pMOve一直到了最左边
    while (stackTop != -1)
    {
        pMove = Stack[stackTop--];  //出栈  此时pMove等于B结点

        //当前结点右结点是否为空或者是否被访问    B结点的右结点不为空,且没有被访问过，则执行else中的语句
        if (pMove->RChild == NULL || pMove->RChild == pLastVisit) //判断当前节点是否为空或这是当前节点的右边结点被访问过了,才可以访问当前结点中的数据
        {
            //当前结点左右结点被访问则打印当前结点中的数据
            cout << pMove->data << "\t";
            pLastVisit = pMove;
        }
        else
        {
            //右边没有被访问
            Stack[++stackTop] = pMove;   //将B结点入栈
            pMove = pMove->RChild;       //设置当前结点为右结点  将当前结点设置为B结点的右结点E
            //使用同样的方法找pMove的最左边      此时还需要去判断E判断E是否有左边结点,   
            while (pMove)
            {
                Stack[++stackTop] = pMove;       //将E结点入栈
                pMove = pMove->LChild;              //E的左结点即为空 
            }

        }
    }
}


int main()
{
    LPTREE A = createNode('A');
    LPTREE B = createNode('B');
    LPTREE C = createNode('C');
    LPTREE D = createNode('D');
    LPTREE E = createNode('E');
    LPTREE F = createNode('F');
    LPTREE G = createNode('G');

    //很死板的创建二叉树方法
    insertNode(A, B, C);
    insertNode(B, D, NULL);
    insertNode(D, NULL, G);
    insertNode(C, E, F);

    cout << "先序遍历" << endl;
    preOrder(A);

    cout << "\n\n非递归方式先序遍历\n" << endl;
    preOderByStack(A);

    cout << "\n\n中序遍历\n";
    midOrder(A);

    cout << "\n\n非递归方式中序遍历\n";
    midOrderByStack(A);

    cout << "\n\n后序遍历\n";
    lastOrder(A);

    cout << "\n\n非递归后序遍历\n";
    lastOrderByStack(A);

    system("pause");
    return 0;
}

执行结果：

(4)层序遍历---使用队列

原理：

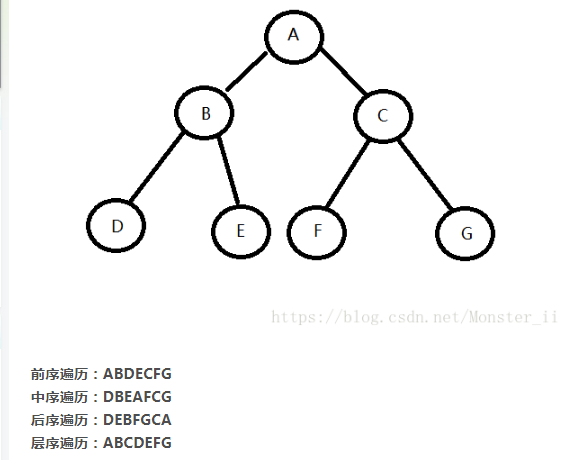
 代码实现：

#include <iostream>
#include <queue>

using namespace std;

struct treeNode
{
    char data;
    treeNode* LChild;
    treeNode* RChild;
};

//typedef struct treeNode* LPTREE;
#define LPTREE treeNode*

//指针一般用LP开头
LPTREE createNode(const char data)  //此处的LPTREE就是一个指针，如果传入的数据为'A',那么'A'就是const类型的,data如果不是const就会报错
{
    LPTREE newNode = (LPTREE)malloc(sizeof(treeNode));
    //LPTREE newNode = new treeNode;
    newNode->data = data;
    newNode->LChild = NULL;
    newNode->RChild = NULL;
    return newNode;
}

//插入数据
void insertNode(LPTREE parentNode, LPTREE LChild, LPTREE RChild)
{
    parentNode->LChild = LChild;
    parentNode->RChild = RChild;
}

//打印当前结点数据
void printCurNodeData(LPTREE curData)
{
    cout << curData->data << "\t";
}

//递归法遍历
//先序遍历：根左右
void preOrder(treeNode* root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        printCurNodeData(root);  //前序遍历先打印根节点  根
        preOrder(root->LChild);  //再打印根节点的左节点  左
        preOrder(root->RChild);  //再打印根节点的右节点  右
    }
}

//中序遍历：左根右
void midOrder(LPTREE root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        midOrder(root->LChild);  //左
        printCurNodeData(root);  //根
        midOrder(root->RChild);  //右
    }
}

//后序遍历：左右根
void lastOrder(LPTREE root)  //传入要打印的树的根节点
{
    if (root != NULL)
    {
        lastOrder(root->LChild);  //左
        lastOrder(root->RChild);  //右
        printCurNodeData(root);   //根
    }
}

//非递归方式前序遍历---使用栈数组
void preOderByStack(LPTREE root)
{
    if (root == NULL)
        return;
    //住准备栈
    LPTREE Stack[10];   //一般使用数组栈，很少再写一个栈实现
    int stackTop = -1;  //栈顶标记
    LPTREE pMove = root;  //从根节点开始打印

    //当栈里面还有路径可以退或者是当前结点pMOve不为空
    while (stackTop != -1 || pMove)
    {
        //根左右
        //下面的这个循环即可找到最左边的节点
        while (pMove)
        {
            //把走过的路径入栈+打印走过的结点
            cout << pMove->data << "\t";    //打印
            Stack[++stackTop] = pMove;  //入栈，一定是++stackTop,因为stackTop初始化为-1
            /*
               如果stackTop初始化为50，则入栈的时候写成stack[++stackTop-50] = pMove;即可
            */
            pMove = pMove->LChild;  //将当前pMove的左节点赋给pMove
        }
        //找到最左边的节点后便无路可走，那么此时出栈
        if (stackTop != -1)
        {
            pMove = Stack[stackTop];  //获取栈顶元素
            stackTop--;  //伪出栈
            pMove = pMove->RChild;    //将当前结点的右结点赋给pMove
        }
    }
}

//非递归方式中序遍历---使用栈数组
/*
01)定义一个指针移动到最左边，把走过的地方入栈
02)无路的时候，出栈，打印当前结点中的元素
03)出栈后，打印当前结点元素，判断当前结点是否存z右边结点，如果存在就去右边
*/
void midOrderByStack(LPTREE root)
{
    if (root == NULL)
        return;
    LPTREE Stack[10];
    int stackTop = -1;

    //定义移动指针，初始化指向根结点root
    LPTREE pMove = root;
    //当栈里面还有路径可以退或者是当前结点pMOve不为空
    while (stackTop != -1 || pMove)
    {
        //走到最左边，把走做的路径入栈
        while (pMove)
        {
            Stack[++stackTop] = pMove;  //将当前结点入栈(走过的结点入栈)
            pMove = pMove->LChild;      //将当前结点的右结点赋给当前结点
        }
        //当当前节点的左结点为空，即无路可走时执行下面代码
        if (stackTop != -1)
        {
            pMove = Stack[stackTop--];  //先将栈中最上面元素赋给pMove：pMove = Stack[stackTop]；然后stackTop--
            cout << pMove->data << "\t";    //打印当前结点根结点中的元素
            pMove = pMove->RChild;
        }
    }
}

//非递归方式后序遍历---使用栈数组
void lastOrderByStack(LPTREE root)
{
    if (root == NULL)
        return;
    LPTREE Stack[10];
    int stackTop = -1;

    //定义移动指针，初始化指向根结点root
    LPTREE pMove = root;

    LPTREE pLastVisit = NULL;  //最后一次访问的标记

    //左 右 根
    while (pMove)
    {
        Stack[++stackTop] = pMove;
        pMove = pMove->LChild;
    }//执行完后，则pMOve一直到了最左边
    while (stackTop != -1)
    {
        pMove = Stack[stackTop--];  //出栈  此时pMove等于B结点

        //当前结点右结点是否为空或者是否被访问    B结点的右结点不为空,且没有被访问过，则执行else中的语句
        if (pMove->RChild == NULL || pMove->RChild == pLastVisit) //判断当前节点是否为空或这是当前节点的右边结点被访问过了,才可以访问当前结点中的数据
        {
            //当前结点左右结点被访问则打印当前结点中的数据
            cout << pMove->data << "\t";
            pLastVisit = pMove;
        }
        else
        {
            //右边没有被访问
            Stack[++stackTop] = pMove;   //将B结点入栈
            pMove = pMove->RChild;       //设置当前结点为右结点  将当前结点设置为B结点的右结点E
            //使用同样的方法找pMove的最左边      此时还需要去判断E判断E是否有左边结点,   
            while (pMove)
            {
                Stack[++stackTop] = pMove;       //将E结点入栈
                pMove = pMove->LChild;              //E的左结点即为空 
            }

        }
    }
}

//层序遍历---使用队列
void levelOrderByQueue(LPTREE root)
{
    if (root == NULL)
        return;
    queue<LPTREE> qu;    //创建队列
    qu.push(root);       //先将根结点入队
    LPTREE pMove;
    while (qu.size() != 0)
    {
        pMove = qu.front();                 //取出队首元素，此时pMove=root
        qu.pop();                         //将队首元素丢弃
        cout << pMove->data << "\t";
        if (pMove->LChild)                 //如果pMove的左结点不为空，则将pMOve的左结点先入队，注必须是左结点先入队
            qu.push(pMove->LChild);
        if (pMove->RChild)               //如果pMove的左结点不为空，则将pMOve的左结点先入队
            qu.push(pMove->RChild);
    }
}



int main()
{
    LPTREE A = createNode('A');
    LPTREE B = createNode('B');
    LPTREE C = createNode('C');
    LPTREE D = createNode('D');
    LPTREE E = createNode('E');
    LPTREE F = createNode('F');
    LPTREE G = createNode('G');

    //很死板的创建二叉树方法
    insertNode(A, B, C);
    insertNode(B, D, NULL);
    insertNode(D, NULL, G);
    insertNode(C, E, F);

    cout << "先序遍历" << endl;
    preOrder(A);

    cout << "\n\n非递归方式先序遍历\n" << endl;
    preOderByStack(A);

    cout << "\n\n中序遍历\n";
    midOrder(A);

    cout << "\n\n非递归方式中序遍历\n";
    midOrderByStack(A);

    cout << "\n\n后序遍历\n";
    lastOrder(A);

    cout << "\n\n非递归后序遍历\n";
    lastOrderByStack(A);

    cout << "\n\n层序遍历\n";
    levelOrderByQueue(A);

    system("pause");
    return 0;
}

测试结果：

3、二叉树中的平衡的概念(顺便引出平衡二叉树的概念)

平衡：当结点固定时，左右子树的高度越接近，这棵二叉树就越平衡
平衡二叉树：根结点的左右子高度差为1

 

 

 

 

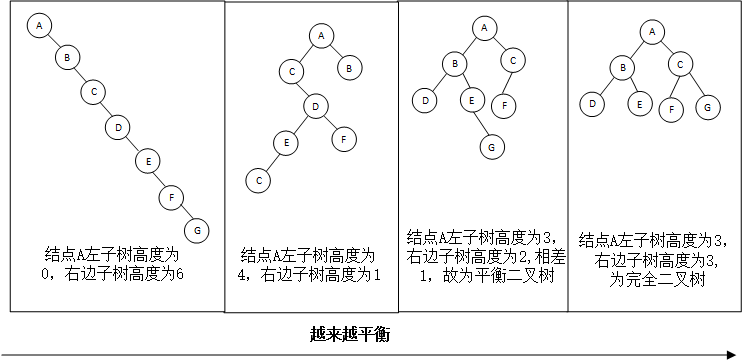
12、C++中的四个智能指针:auto_ptr,shared_ptr,weak_ptr,unique_ptr，其中auto_ptr已经被C++11抛弃

1、auto_ptr(C++98中的放案,C++11已经抛弃)

//auto_ptr
#include <iostream>
#include <memory>  //for auto_ptr、shared_ptr...
#include <string>

using namespace std;

class Test
{
private:
    string str;
public:
    Test(string s):str(s)     //使用成员初始化列表为类私有数据赋值
    {
        cout << "Tets类对象已创建: " << str << "\n";
    }
    ~Test()
    {
        cout << "Test类对象已删除：" << str << endl;
    }
    string & getStr()
    {
        return str;  //返回私有数据
    }
    void setStr(string s)
    {
        str = s;
    }
    void print()
    {
        cout << str << endl;  //访问Test类对象指针p的数据
    }
};

int main()
{
    //为了更好的观察到类对象指针pTest被释放的过程，此处加一个大括号
    {
        auto_ptr<Test> pTest(new Test("123"));  //使用auto_ptr创建指向Test类对象的指针pTest,当pTest过期时候自动释放内存
        pTest->setStr("HelloWorld");            //修改pTest指向的Test类对象中数据的内容
        pTest->print();                         //打印pTest指向的Test类对象中数据的内容


        /*
        auto_ptr类成员函数reset()的使用
        01)使用auto_ptr类成员函数对pTest指向的对象重新绑定,此时auto_ptr会释放掉pTest原指向的内存,相当于原类对象不存在了,故会调用Test析构函数;
           创建pTest新指向的类对象,故会调用pTest构造函数
        03)故下面这句会调用Test类析构函数和构造函数,而auto_ptr释放掉原pTest指向的类对象内存是默默执行的
        04)当我们想要在中途释放资源，而不是等到智能指针被析构时才释放，我们可以使用ptest.reset(); 语句
        */
        pTest.reset(new Test("123")); 
        pTest->print();


        /*
        auto_ptr类成员函数release()的使用
        */        
        pTest.release(); //只是将pTest赋值为空,但是它原来指向的内存并没有被释放(没有执行Test的析构函数),相当于它只是释放了对资源的所有权
    }

    system("pause");
    return 0;
}



/*
使用成员初始化列表的原因：
在创建继承类对象时候。需要首先对基类中的私有数据进行赋值，再对继承类中的私有数据进行赋值，
这个时候要是用成员初始化列表
*/

运行结果：

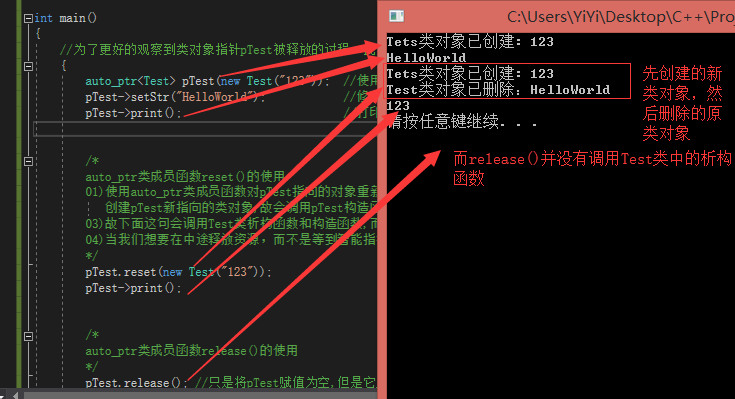
2、auto_ptr存在的问题：

但是下面的语句将有潜在的问题

auto_ptr<string> pStr1(new string("Hello"));
auto_ptr<string> pStr2;
pStr2 = pStr1;

此时理论上第三行不会报，错实际上在VS2017下已报错，pStr2剥夺了pStr1的所有权，pStr1变成了空指针，当程序运行时访问pStr1将会报，如果pStr2原来不是空指针，那么auto_ptr会释放掉pStr2原来指向的内存，基于这个原因，应该避免把auto_ptr放到容器中，因为算法对容器操作时，很难避免STL内部对容器实现了赋值传递操作，这样会使容器中很多元素被置为NULL。判断一个智能指针是否为空不能使用if(ptest == NULL)，应该使用if(ptest.get() == NULL)。
所以auto_ptr的缺点是：存在潜在的内存崩溃问题！

2、unique_ptr

unique_ptr 是一个独享所有权的智能指针，它提供了严格意义上的所有权，包括：
1)、拥有它指向的对象
2)、无法进行复制构造，无法进行复制赋值操作。即无法使两个unique_ptr指向同一个对象。但是可以进行移动构造和移动赋值操作(使用move()函数)
      方法如下：

unique_ptr<Test> ptest(new Test("123"));//调用构造函数，输出Test creat
unique_ptr<Test> ptest2(new Test("456"));//调用构造函数，输出Test creat
ptest->print();//输出123
ptest2 = std::move(ptest);//不能直接ptest2 = ptest，调用了move后ptest2原本的对象会被释放，ptest2对象指向原本ptest对象的内存,最后ptest变为空指针，输出Test delete 456
if (ptest == NULL)
    cout << "ptest = NULL\n";//因为两个unique_ptr不能指向同一内存地址，所以经过前面move后ptest会被赋值NULL，输出ptest=NUL

3)、保存指向某个对象的指针，当它本身被删除释放的时候，会使用给定的删除器释放它指向的对象

 具体使用方法：

//#include <iostream>
//
//using namespace std;
//
//struct treeNode
//{
//    char data;
//    treeNode* LChild;
//    treeNode* RChild;
//};
//
////typedef struct treeNode* LPTREE;
//#define LPTREE treeNode*
//
////指针一般用LP开头
//LPTREE createNode(const char data)  //此处的LPTREE就是一个指针，如果传入的数据为'A',那么'A'就是const类型的,data如果不是const就会报错
//{
//    LPTREE newNode = (LPTREE)malloc(sizeof(treeNode));
//    //LPTREE newNode = new treeNode;
//    newNode->data = data;
//    newNode->LChild = NULL;
//    newNode->RChild = NULL;
//    return newNode;
//}
//
////插入数据
//void insertNode(LPTREE parentNode, LPTREE LChild, LPTREE RChild)
//{
//    parentNode->LChild = LChild;
//    parentNode->RChild = RChild;
//}
//
////打印当前结点数据
//void printCurNodeData(LPTREE curData)
//{
//    cout << curData->data << "\t";
//}
//
////递归法遍历
////先序遍历：根左右
//void preOrder(treeNode* root)  //传入要打印的树的根节点
//{
//    if (root != NULL)
//    {
//        printCurNodeData(root);  //前序遍历先打印根节点  根
//        preOrder(root->LChild);  //再打印根节点的左节点  左
//        preOrder(root->RChild);  //再打印根节点的右节点  右
//    }
//}
//
////中序遍历：左根右
//void midOrder(LPTREE root)  //传入要打印的树的根节点
//{
//    if (root != NULL)
//    {
//        midOrder(root->LChild);  //左
//        printCurNodeData(root);  //根
//        midOrder(root->RChild);  //右
//    }
//}
//
////后序遍历：左右根
//void lastOrder(LPTREE root)  //传入要打印的树的根节点
//{
//    if (root != NULL)
//    {
//        lastOrder(root->LChild);  //左
//        lastOrder(root->RChild);  //右
//        printCurNodeData(root);   //根
//    }
//}
//
////非递归方式前序遍历---使用栈数组
//void preOderByStack(LPTREE root)
//{
//    if (root == NULL)
//        return;
//    //住准备栈
//    LPTREE Stack[10];   //一般使用数组栈，很少再写一个栈实现
//    int stackTop = -1;  //栈顶标记
//    LPTREE pMove = root;  //从根节点开始打印
//
//    //当栈里面还有路径可以退或者是当前结点pMOve不为空
//    while (stackTop != -1 || pMove)
//    {
//        //根左右
//        //下面的这个循环即可找到最左边的节点
//        while (pMove)
//        {
//            //把走过的路径入栈+打印走过的结点
//            cout << pMove->data << "\t";    //打印
//            Stack[++stackTop] = pMove;  //入栈，一定是++stackTop,因为stackTop初始化为-1
//            /*
//               如果stackTop初始化为50，则入栈的时候写成stack[++stackTop-50] = pMove;即可
//            */
//            pMove = pMove->LChild;  //将当前pMove的左节点赋给pMove
//        }
//        //找到最左边的节点后便无路可走，那么此时出栈
//        if (stackTop != -1)
//        {
//            pMove = Stack[stackTop];  //获取栈顶元素
//            stackTop--;  //伪出栈
//            pMove = pMove->RChild;    //将当前结点的右结点赋给pMove
//        }
//    }
//}
//
////非递归方式中序遍历---使用栈数组
///*
//01)定义一个指针移动到最左边，把走过的地方入栈
//02)无路的时候，出栈，打印当前结点中的元素
//03)出栈后，打印当前结点元素，判断当前结点是否存z右边结点，如果存在就去右边
//*/
//void midOrderByStack(LPTREE root)
//{
//    if (root == NULL)
//        return;
//    LPTREE Stack[10];
//    int stackTop = -1;
//
//    //定义移动指针，初始化指向根结点root
//    LPTREE pMove = root;
//    //当栈里面还有路径可以退或者是当前结点pMOve不为空
//    while (stackTop != -1 || pMove)
//    {
//        //走到最左边，把走做的路径入栈
//        while (pMove)
//        {
//            Stack[++stackTop] = pMove;  //将当前结点入栈(走过的结点入栈)
//            pMove = pMove->LChild;      //将当前结点的右结点赋给当前结点
//        }
//        //当当前节点的左结点为空，即无路可走时执行下面代码
//        if (stackTop != -1)
//        {
//            pMove = Stack[stackTop--];  //先将栈中最上面元素赋给pMove：pMove = Stack[stackTop]；然后stackTop--
//            cout << pMove->data << "\t";    //打印当前结点根结点中的元素
//            pMove = pMove->RChild;
//        }
//    }
//}
//
////非递归方式后序遍历---使用栈数组
//void lastOrderByStack(LPTREE root)
//{
//    if (root == NULL)
//        return;
//    LPTREE Stack[10];
//    int stackTop = -1;
//
//    //定义移动指针，初始化指向根结点root
//    LPTREE pMove = root;
//
//    LPTREE pLastVisit = NULL;  //最后一次访问的标记
//
//    //左 右 根
//    while (pMove)
//    {
//        Stack[++stackTop] = pMove;
//        pMove = pMove->LChild;
//    }//执行完后，则pMOve一直到了最左边
//    while (stackTop != -1)
//    {
//        pMove = Stack[stackTop--];  //出栈  此时pMove等于B结点
//
//        //当前结点右结点是否为空或者是否被访问    B结点的右结点不为空,且没有被访问过，则执行else中的语句
//        if (pMove->RChild == NULL || pMove->RChild == pLastVisit) //判断当前节点是否为空或这是当前节点的右边结点被访问过了,才可以访问当前结点中的数据
//        {
//            //当前结点左右结点被访问则打印当前结点中的数据
//            cout << pMove->data << "\t";
//            pLastVisit = pMove;
//        }
//        else
//        {
//            //右边没有被访问
//            Stack[++stackTop] = pMove;   //将B结点入栈
//            pMove = pMove->RChild;       //设置当前结点为右结点  将当前结点设置为B结点的右结点E
//            //使用同样的方法找pMove的最左边      此时还需要去判断E判断E是否有左边结点,   
//            while (pMove)
//            {
//                Stack[++stackTop] = pMove;       //将E结点入栈
//                pMove = pMove->LChild;              //E的左结点即为空 
//            }
//
//        }
//    }
//}
//
//
//int main()
//{
//    LPTREE A = createNode('A');
//    LPTREE B = createNode('B');
//    LPTREE C = createNode('C');
//    LPTREE D = createNode('D');
//    LPTREE E = createNode('E');
//    LPTREE F = createNode('F');
//    LPTREE G = createNode('G');
//
//    //很死板的创建二叉树方法
//    insertNode(A, B, C);
//    insertNode(B, D, NULL);
//    insertNode(D, NULL, G);
//    insertNode(C, E, F);
//
//    cout << "先序遍历" << endl;
//    preOrder(A);
//
//    cout << "\n\n非递归方式先序遍历\n" << endl;
//    preOderByStack(A);
//
//    cout << "\n\n中序遍历\n";
//    midOrder(A);
//
//    cout << "\n\n非递归方式中序遍历\n";
//    midOrderByStack(A);
//
//    cout << "\n\n后序遍历\n";
//    lastOrder(A);
//
//    cout << "\n\n非递归后序遍历\n";
//    lastOrderByStack(A);
//
//    system("pause");
//    return 0;
//}

//auto_ptr
#include <iostream>
#include <memory>  //for auto_ptr、shared_ptr...
#include <string>

using namespace std;

class Test
{
private:
    string str;
public:
    Test(string s):str(s)     //使用成员初始化列表为类私有数据赋值
    {
        cout << "Tets类对象已创建: " << str << "\n";
    }
    ~Test()
    {
        cout << "Test类对象已删除：" << str << endl;
    }
    string & getStr()
    {
        return str;  //返回私有数据
    }
    void setStr(string s)
    {
        str = s;
    }
    void print()
    {
        cout << str << endl;  //访问Test类对象指针p的数据
    }
};

int main()
{
    //为了更好的观察到类对象指针pTest被释放的过程，此处加一个大括号
    {
        unique_ptr<Test> pTest(new Test("123"));  //使用auto_ptr创建指向Test类对象的指针pTest,当pTest过期时候自动释放内存
        pTest->setStr("HelloWorld");            //修改pTest指向的Test类对象中数据的内容
        pTest->print();                         //打印pTest指向的Test类对象中数据的内容


        /*
        auto_ptr类成员函数reset()的使用
        01)使用auto_ptr类成员函数对pTest指向的对象重新绑定,此时auto_ptr会释放掉pTest原指向的内存,相当于原类对象不存在了,故会调用Test析构函数;
           创建pTest新指向的类对象,故会调用pTest构造函数
        03)故下面这句会调用Test类析构函数和构造函数,而auto_ptr释放掉原pTest指向的类对象内存是默默执行的
        04)当我们想要在中途释放资源，而不是等到智能指针被析构时才释放，我们可以使用ptest.reset(); 语句
        */
        pTest.reset(new Test("123")); 
        pTest->print();


        /*
        auto_ptr类成员函数release()的使用
        */        
        pTest.release(); //只是将pTest赋值为空,但是它原来指向的内存并没有被释放(没有执行Test的析构函数),相当于它只是释放了对资源的所有权
    }

    system("pause");
    return 0;
}



/*
使用成员初始化列表的原因：
在创建继承类对象时候。需要首先对基类中的私有数据进行赋值，再对继承类中的私有数据进行赋值，
这个时候要是用成员初始化列表
*/

另外unique_ptr还有更聪明的地方：当程序试图将一个 unique_ptr 赋值给另一个时，如果源 unique_ptr 是个临时右值，编译器允许这么做；如果源 unique_ptr 将存在一段时间，编译器将禁止这么做，比如：

unique_ptr<string> pu1(new string ("hello world")); 
unique_ptr<string> pu2; 
pu2 = pu1;                                      // #1 不允许
unique_ptr<string> pu3; 
pu3 = unique_ptr<string>(new string ("You"));   // #2 允许

其中#1留下悬挂的unique_ptr(pu1)，这可能导致危害。而#2不会留下悬挂的unique_ptr，因为它调用 unique_ptr 的构造函数，该构造函数创建的临时对象在其所有权让给 pu3 后就会被销毁。这种随情况而已的行为表明，unique_ptr 优于允许两种赋值的auto_ptr 。

注：如果确实想执行类似与#1的操作，要安全的重用这种指针，可给它赋新值。C++有一个标准库函数std::move()，让你能够将一个unique_ptr赋给另一个。尽管转移所有权后 还是有可能出现原有指针调用（调用就崩溃）的情况。但是这个语法能强调你是在转移所有权，让你清晰的知道自己在做什么，从而不乱调用原有指针。

3、shared_ptr

多个shared_ptr指针可以指向相同对象，该对象和其相关资源会在“最后一个引用被销毁”时候释放。

它使用计数机制来表明资源被几个指针共享。可以通过成员函数use_count()来查看资源的所有者个数。除
了可以通过new来构造，还可以通过传入auto_ptr, unique_ptr,weak_ptr来构造。当我们调用release()时，
当前指针会释放资源所有权，计数减一。当计数等于0时，资源会被释放。

shared_ptr类中新建了Counter类对象s,当进行shared_ptr类指针赋值或复制时候，将调用shared_ptr类中的赋值构造函数和复制构造函数，此时将Counter类对象s中的一个int型变量进行自加一即可。

string *pStr = new string("123");
shared_ptr<string> p1(pStr);  //将p1指向pStr指向的内存区域，在shared_ptr构造函数中Counter类对象中的int型变量赋值为1
shared_ptr<string> p2;
p2=p1;  //将调用shared_ptr类中的赋值构造函数,在该函数中将Counter类对象中的int型变量自加一
int a = p1.use_count();  //a=2
int b = p2.use_count();  //b=2

复习何时调用赋值构造函数和复制构造函数：

//假设Test是一个类
Test dog("Hello");
Test cat = dog;  //cat类对象初始化，将调用Test类中的复制构造函数Test(cosnt Test & t)
Test bird;
bird = dog;  //将调用赋值构造函数(对等号的重载) Test & operator=(const Test & t)

 shared_ptr的具体使用方

//shared_ptr
#include <iostream>
#include <memory>  //for auto_ptr、shared_ptr...
#include <string>

using namespace std;

class Test
{
private:
    string str;
public:
    Test(string s):str(s)     //使用成员初始化列表为类私有数据赋值
    {
        cout << "Tets类对象已创建: " << str << "\n";
    }
    ~Test()
    {
        cout << "Test类对象已删除：" << str << endl;
    }
    string & getStr()
    {
        return str;  //返回私有数据
    }
    void setStr(string s)
    {
        str = s;
    }
    void print()
    {
        cout << str << endl;  //访问Test类对象指针p的数据
    }
};

int main()
{
    //为了更好的观察到类对象指针pTest被释放的过程，此处加一个大括号
    {
        shared_ptr<Test> pTest1(new Test("123")); //调用shred_ptr类中的构造函数,并将Counter类对象中int型变量赋值为1
        pTest1->setStr("HelloWorld");             //修改pTest1指向的Test类对象中数据的内容
        pTest1->print();                          //打印pTest1指向的类对象中的内容

        shared_ptr<Test> pTest2;
        pTest2 = pTest1;                                       //调用shared_ptr类中的赋值构造函数,并将Counter类对象中int型变量自加1
        cout << "pTest1.use_count=" << pTest1.use_count() << endl;   //查看pTest1对象下Counter类对象中int型变量的值
        cout << "pTest2.use_count=" << pTest2.use_count() << endl;   //查看pTest2对象下Counter类对象中int型变量的值  一样的，由于use_count()是shared_ptr类函数,故使用.来访问use_count()

        /*Test* pTest3 = new Test("456");
        shared_ptr<Test> pTest4(pTest3);*/  //这样创建的shred_ptr指针不可以使用swap()

        shared_ptr<Test> pTest4(new Test("pTest4"));
        cout << "pTest1= " << (pTest1.get()) << endl;       //查看pTest1指向的对象的地址
        cout << "pTest2= " << (pTest2.get()) << endl;       //查看pTest2指向的对象的地址
        cout << "pTest4= " << (pTest4.get()) << endl;       //查看pTest3指向的对象的地址
        cout << "pTest1.use_count=" << pTest1.use_count() << endl;
        cout << "pTest4.use_count=" << pTest4.use_count() << endl;
        cout << "执行swap(pTest1,pTest4)\n";
        swap(pTest1, pTest4);                              //原来pTest2和pTest1指向相同的类对象,交换之后pTest2还是指向原来的类对象,pTest1指向的类对象变了
        cout << "pTest1= " << (pTest1.get()) << endl;       //查看pTest1指向的对象的地址
        cout << "pTest2= " << (pTest2.get()) << endl;       //查看pTest2指向的对象的地址
        cout << "pTest4= " << (pTest4.get()) << endl;       //查看pTest3指向的对象的地址
        cout << "pTest1.use_count=" << pTest1.use_count() << endl;
        cout << "pTest4.use_count=" << pTest4.use_count() << endl;


        cout << "执行pTest2.reset(new Test(789))\n";
        pTest2.reset(new Test("789")); //更改pTest2指向的对象中的内容，会引起pTest对象中Counter类对象中int型变量减1
        pTest2->print();       //pTest作为指向Test类对象的指针访问Test类中的方法
        cout << "pTest1.use_count=" << pTest1.use_count() << endl;   //查看pTest1对象下Counter类对象中int型变量的值
        cout << "pTest2.use_count=" << pTest2.use_count() << endl;   //查看pTest2对象下Counter类对象中int型变量的值
        cout << "pTest4.use_count=" << pTest4.use_count() << endl;
        //pTest2.release(); //shared_ptr中没有release()
    }

    system("pause");
    return 0;
}

执行结果：

shared_ptr使用一个类实现

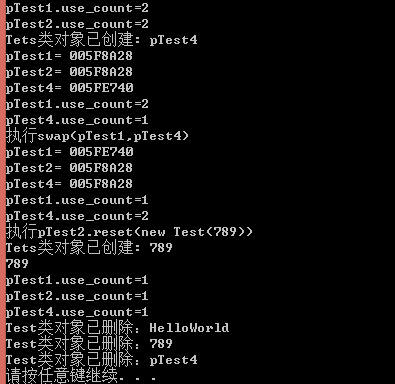
4、weak_ptr

weak_ptr是用来解决shared_ptr相互引用时的死锁问题, 如果说两个shared_ptr相互引用, 那么这两个指针的引用计数永远不可能下降为0, 资源永远不会释放。如下将会出现shared_ptr互锁的现象

详细的shraed_ptr出现互锁的例子：

#include <iostream>  
using namespace std;  
  
#include <memory>  
#include "SharedPtr.h"  
  
struct Node  
{  
    Node(int va)  
        :value(va)  
          
    {  
        cout<<"Node()"<<endl;  
    }  
  
  
    ~Node()  
    {  
        cout<<"~Node()"<<endl;  
    }  
    shared_ptr<Node> _pre;  
    shared_ptr<Node> _next;  
    int value;  
};  
  
void funtest()  
{  
    shared_ptr<Node> sp1(new Node(1));  
    shared_ptr<Node> sp2(new Node(2));  
  
    sp1->_next=sp2;  
    sp2->_pre=sp1;  
}  
int main()  
{  
    funtest();  
    return 0;  
}  

以上代码参考博客 

 

shared_ptr<B> pb(new B());
shared_ptr<A> pa(new A());
pb->pa_ = pa;
pa->pb_ = pb;

waek_ptr的赋值构造函数形式为：WeakPtr<T> &operator=(SharePtr<T> &s);可以看出weak_prt的赋值构造函数形参为shared_ptr
于是可以将shared_ptr指针赋值给weak_ptr指针，但是在该赋值构造函数下，引用计数并没有自加1，从而不会引起函数执行完后引用计数不为0的情况
以下将会解决问题：

shared_ptr<B> pb(new B());
weak_ptr<A> pa(new A());
pb->pa_ = pa;
pa->pb_ = p

5、总结

总结：
由于在使用new创建指针时候，可能存在忘记加delete从而导致出现内存泄漏的情况，于是引入了智能指针
首先是auto_ptr它可以在类构造函数中为指针分配内存空间，在析构函数中释放内存，当指针结束生命周期时候就会自动调用析构函
数
以释放内存空间。但是auto_ptr指针之间不可以相互赋值，编译器会报错
再者就是unique_ptr，它弥补了auto_ptr的缺点，两个指针之间可以赋值，通过类方法move()实现，假如p1=p2，那么p2就会成为空指针，可能以后还会使用p2
故也存在风险
还有就是shared_ptr,它引入了一个引用计数的概念，在构造函数中将该引用计数赋值为1，在和赋值、复制构造函数中都将该引用计数自加1。
在需要将shred_ptr指针销毁的时候，会将该引用计数自减1，等到该引用计数为0时候就会调用析构函数释放内存。
最后就是weak_ptr引入主要是为了解决shred_ptr自锁的问题，解决方法是在类构造函数、赋值构造函数中将shared_ptr类对象作为形参，但是在构造函数和赋值构造函数
、复制构造函数中没有引入引用计数
注：引用计数可以是一个类对象中的一个int型变量

6、测试两个普通指针是否可以指向同一块内存区域

//测试两个普通指针是否可以指向同一块内存区域
#include <iostream>
using namespace std;
class A
{
private:
    int aa;
public:
    A(int temp) :aa(temp) {}
    void dis()
    {
        cout << aa << endl;
    }
};
int main()
{
    A a(112);  //创建一个指向A类对象的指针p_a
    A* p_b;
    A* p_c;
    p_b = &a;
    p_c = p_b;
    p_b->dis();
    p_c->dis();    //即允许两个普通指针同时指向一块内存区域，但是指针指针auto_ptr和unique_ptr是不允许的

    system("pause");
    return 0;
}

不允许将一个auto_ptr指针赋值给另外一个auto_ptr指针的原因是：
假如有两个auto_ptr指针p1和p2，如果将p2赋给p1，那么p2指向的内存会被释放掉，此时p2指针为空指针，再使用p2指针的时候会出错

结果是两个普通指针可以指向同一块内存区域

7、VS2017环境下内存泄漏检测

VS中自带了内存泄露检测工具，若要启用内存泄露检测，则在程序中包括以下语句：

#define _CRTDBG_MAP_ALLOC
#include <crtdbg.h>

它们的先后顺序不能改变。通过包括 crtdbg.h，将malloc和free函数映射到其”Debug”版本_malloc_dbg和_free_dbg，这些函数将跟踪内存分配和释放。此映射只在调试版本(在其中定义了_DEBUG)中发生。#define语句将CRT堆函数的基版本映射到对应的”Debug”版本。
测试代码如下

//以下两条语句顺序不可改变
#define _CRTDBG_MAP_ALLOC  //将 CRT 堆函数的基版本映射到对应的“Debug”版本。 并非绝对需要该语句；但如果没有该语句，内存泄漏转储包含的有用信息将较少。
#include <crtdbg.h>

#include <iostream>
using namespace std;

void getMemory(char* p, int num)
{
    //p = new char[num];                  //new分配的内存不可以定位到内存泄漏的行数
    p = (char*)malloc(sizeof(char)*num);  //maloc分配的内存可以定位到内存泄漏的行数
}

int main()
{
    char* str = NULL;
    getMemory(str, 100);
    cout << "Memory leak test!" << endl;
    _CrtDumpMemoryLeaks();                //将在输出窗口输出内存泄漏信息

    system("pause");
    return 0;
}

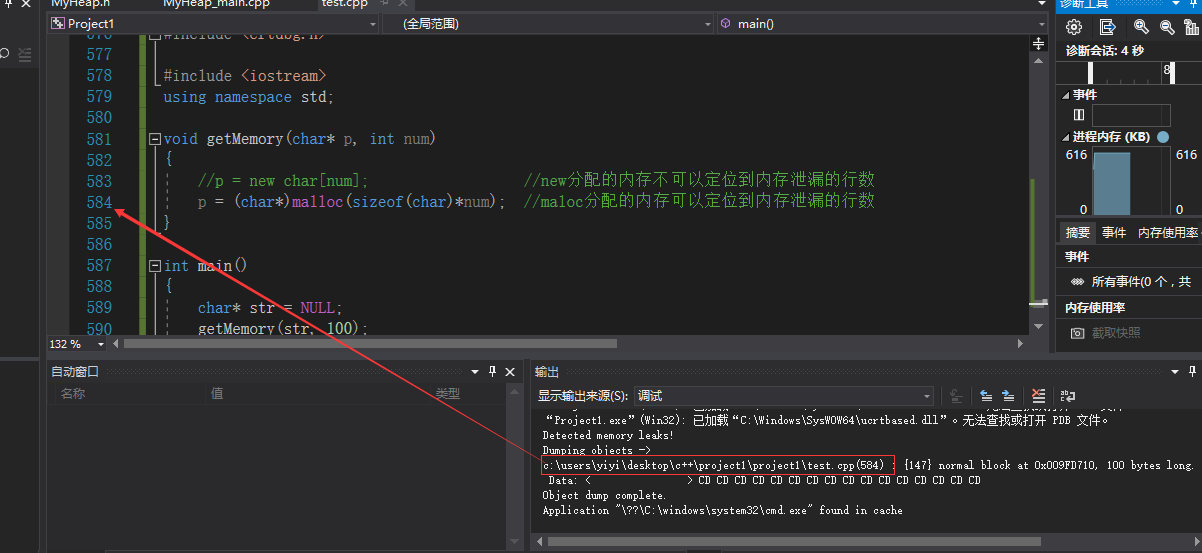
内存泄露检测之使用CRT的Debug技术
基本原理
内存泄露主要指的是我们分配的堆内存没有被释放，随着程序的运行，可能会积少成多，导致系统可用内存降低，甚至造成系统瘫痪。一般分配堆内存的C++方式有：
malloc
new
        当然，如果说更深一层，new最终调用的是malloc，而malloc调用的则是Windows API堆分配函数（如：HeapAlloc）来进行分配堆内存的。但平常我们并不直接调用很底层的函数。
　　Debug版本的 CRT定义了一套调试版本的内存分配函数（如_malloc_dbg)。当你包含了CRTDBG.h后，如果当前是Debug工程，十有八九会有_DEBUG宏，这时，malloc函数会被被映射为_malloc_dbg。
　　当如果是Release版本，它什么都不做。这样以来，如果是Debug版本，我们调用的malloc或者new，其实最终调用的都是_malloc_dbg。而_malloc_dbg会分配多于我们指定的内存大小，用来存储调试信息，用来跟踪内存分配和释放是否对应。
　　现在，我们可以暂时想象CRT是如何跟踪内存泄露的：调用_malloc_dbg，它将分配一个内存地址，将地址存储到一个列表中，当调用free的时候，肯定还是传入该地址，然后从列表中移除。当程序结束的时候，如果没有内存泄露，这个列表就应该为空，如果不为空，那么就出现了内存泄露，CRT库就将这些地址打印到调试窗口中，编译程序员进行排查。当然这个过程要比我说的复杂很多，但原理都差不多。
　　当然，这一切的前提，都是你得直接或者间接的调用malloc，不然一切都是空谈。

以上所有的技术针对的都是针对于malloc，我也说了new最终调用的也是malloc，那new应该也会有效。的确，new的确起了作用，但你会发现，你基本上无法定位你是在哪里调用的new，因为没有源码行号显示，原因是new可能经过了几层调用，才调用到了malloc，而且是在CRT库中调用的malloc，打印的地址，也是CRT的地址，显然这是不对的。CRT虽然是C Rumtime library，但他照顾了C++一些特性，例如new。Debug CRT重载了new，实现了Debug版本的new。所以，我们要多做一些工作，让其正确工作：

//for new显示内存泄漏的行号
#ifdef _DEBUG
#ifndef DBG_NEW
    #define DBG_NEW new ( _NORMAL_BLOCK , __FILE__ , __LINE__ )
    #define new DBG_NEW
#endif
#endif // _DEBUG

//for new显示内存泄漏的行号
#ifdef _DEBUG
#ifndef DBG_NEW
    #define DBG_NEW new ( _NORMAL_BLOCK , __FILE__ , __LINE__ )
    #define new DBG_NEW
#endif
#endif // _DEBUG

//以下两条语句顺序不可改变
#define _CRTDBG_MAP_ALLOC  //将 CRT 堆函数的基版本映射到对应的“Debug”版本。 并非绝对需要该语句；但如果没有该语句，内存泄漏转储包含的有用信息将较少。
#include <crtdbg.h>

#include <iostream>
using namespace std;

void getMemory(char** p, int num)  //这里必须设置成二级指针，否则实参的值是不会变的
{
    *p = new char[num];                  //new分配的内存不可以定位到内存泄漏的行数
    //*p = (char*)malloc(sizeof(char)*num);  //maloc分配的内存可以定位到内存泄漏的行数
    cout << "子函数中p指向的内存地址为:"<< (void*)(*p) << endl;
}

int main()
{
    char* str = NULL;
    getMemory(&str, 100);
    cout << "主函数中str指向的内存地址:" << (void*)str << endl;
    cout << sizeof(str) << endl;
    cout << "Memory leak test!" << endl;
    _CrtDumpMemoryLeaks();                //将在输出窗口输出内存泄漏信息

    delete [] str;

    system("pause");
    return 0;
}

运行结果：

由于主函数中的str和p指向同一块内存，故只在主函数中使用了delete [] str; 没有在子函数中使用delete [] p
故此时出现了报错：

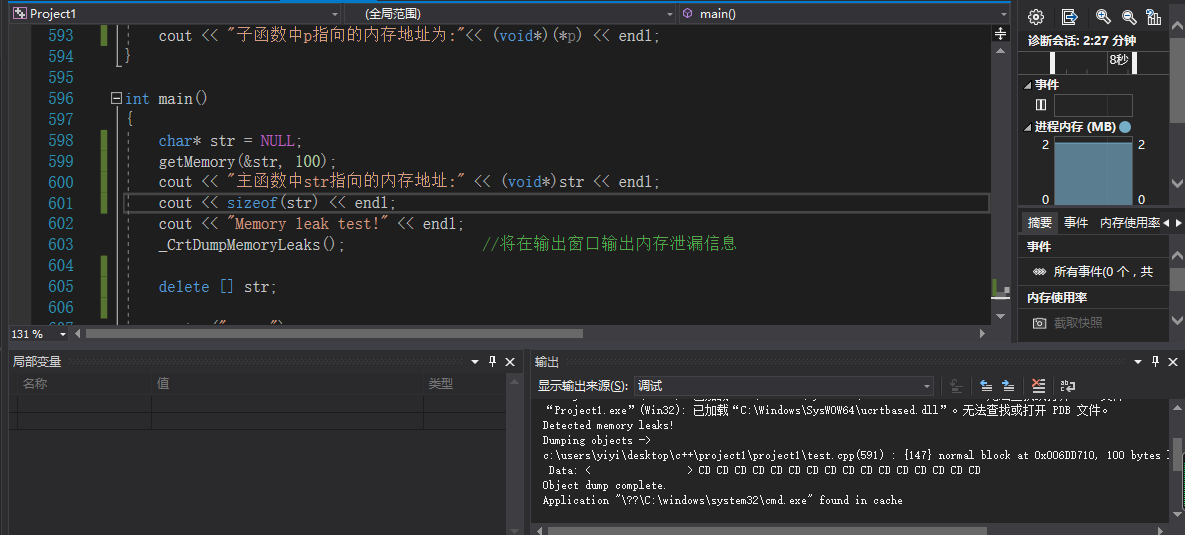
但是，如果程序可能会在多个地方退出该怎么办呢？在每一个可能的出口处调用 _CrtDumpMemoryLeaks 肯定是不可取的，那么这时可以在程序开始处包含下面的调用：_CrtSetDbgFlag ( _CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF );这条语句无论程序在什么地方退出都会自动调用 _CrtDumpMemoryLeaks。注意：这里必须同时设置两个位域标志：_CRTDBG_ALLOC_MEM_DF 和 _CRTDBG_LEAK_CHECK_DF。

参考博客：

https://blog.csdn.net/hongxingabc/article/details/49873541?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

https://blog.csdn.net/song_lipeng/article/details/102931987

8、make_shared  m128

#include <iostream>
#include <memory>    //for shared_ptr
#include <vector>
#include <string>

using namespace std;

int main()
{
    shared_ptr<string> p1 = make_shared<string>("Hello");  //p1指向字符串Hello
    shared_ptr<string> p2 = make_shared<string>(10, 'H');  //p2指向十个H，即"HHHH...."
    shared_ptr<string> p3 = make_shared<string>();         //p3指向NULL

    cout << p1 << endl;   //打印p1指向的地址
    cout << p2 << endl;

    cout << *p1 << endl;  //打印Helllo
    cout << *p2 << endl;

    system("pause");
    return 0;

}

运行结果：

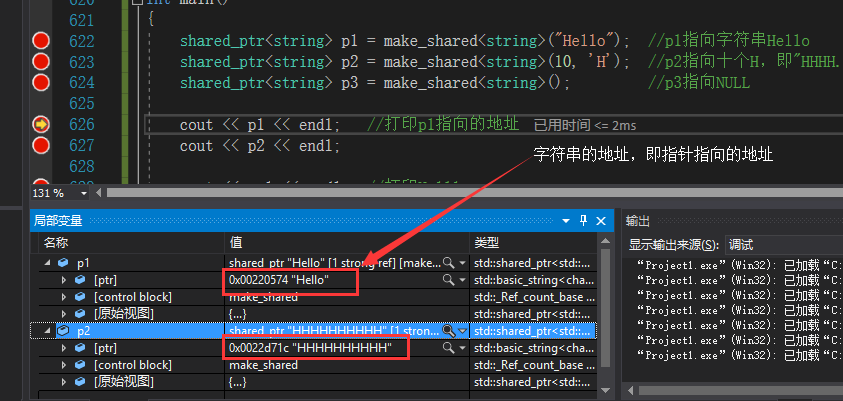
 make_shared和new的区别

make_shared函数的主要功能是在动态内存中分配一个对象并初始化它，返回指向此对象的shared_ptr
new先在堆上分配一块内存用来使用，然后再给智能控制块分配一块内存，但是这两个内存区域是不连续的
make_shared在堆上分配一个足够大的内存，其中包含两部分，上部分是内存(用来使用),下面是智能指针控制块
因此make_shared分配的内存是连续的，访问速度较快

13、友元函数复习

1、以前学习的友元类传送门

2、复习

#include <iostream>

using namespace std;

class A
{
private:
    int dog;
    friend class B;    //使类B成为类A的友元类，以便于在类B中的方法实现里访问类A中的私有数据
public:
    A(int t) :dog(t) {};

};
class B
{
private:
    A a;  //只不过在创建B的类对象时候，需要传入一个A的类对象

public:
    B(A test) :a(test) {};
    void dis()
    {
        cout << "类B中的方法，但是访问的是类A中的数据" << a.dog << endl;
    }

};
int main()
{
    A a(112);  //创建A的类对象
    B b(a);
    b.dis();

    system("pause");
    return 0;

}

假如将类A中的friend class B;去掉，那么会报错如下：

恢复后正常执行如下：

14、虚函数复习

C++的虚函数主要作用是“运行时多态”，父类中提供虚函数的实现，为子类提供默认的函数实现。

子类可以重写父类的虚函数实现子类的特殊化。

1、虚函数和普通函数的区别

假如有两个基类指针，分别指向了一个基类对象和一个继承类对象，然后该基类指针调用了基类和继承类下的一个方法
假如该方法是虚函数，那么要根据基类指针指向的对象去判断执行基类方法还是继承类方法
加入该方法是普通函数，那么两个基类指针调用的都是基类中的方法

原理：

虚函数主要是通过虚函数表和虚函数指针来实现。
虚函数表存放类中函数的地址，加入继承类重写了基类中的虚函数，在继承类的虚函数表中会将基类对应的函数地址覆盖掉；
虚函数指针存放在类对象中(会放在类对象地址开始处)，并且它执行该类对象所在的虚函数表。

普通函数不存在虚函数表，它只有一个函数地址，不存在继承类函数地址覆盖掉基类函数地址的情况，一般是基类强制子类使用
某个函数

2、纯虚函数

C++中包含纯虚函数的类，被称为是“抽象类”。抽象类不能使用new出对象，只有实现了这个纯虚函数的子类才能new出对象。

C++中的纯虚函数更像是“只提供申明，没有实现”，是对子类的约束，是“接口继承”。

C++中的纯虚函数也是一种“运行时多态”。

4、函数指针定义方法

/*函数指针实现方法一*/
//形式1：返回类型(*函数名)(参数表)

/*函数指针实现方法一*/
//形式1：返回类型(*函数名)(参数表)
#include <iostream>

using namespace std;

char fun(int a)
{
    cout << a << endl;
    return 0;
}

int main()
{
    char(*pFun)(int);  //定义一个函数指针，它可以指向一个返回值为char型变量、形参为int型变量的函数

    pFun = fun;
    (*pFun)(112);  //执行fun()函数，和fun(112);效果是一样的

    system("pause");
    return 0;
}

/*函数指针实现方法二*/
//形式2：typedef 返回类型(*新类型)(参数表)

/*函数指针实现方法二*/
//形式2：typedef  返回类型(*新类型)(参数表)
#include <iostream>

using namespace std;

char fun(int a)
{
    cout << a << endl;
    return 0;
}

int main()
{
    typedef char(*PTRFUN)(int);  //定义一个函数指针，它可以指向一个返回值为char型变量、形参为int型变量的函数
    PTRFUN pFun;                 //像int、char等类型一样使用PTRFUN

    pFun = fun;
    (*pFun)(112);  //执行fun()函数，和fun(112);效果是一样的

    system("pause");
    return 0;
}

注typedef最常用：

int i;//定义一个整型变量i  
typedef myInt int；
myInt j;//定义一个整型变量

 5、虚函数表的进一步解释

 

 

15、堆排序(重新学习)

1、一个一个的插入实现方法

c malloc 堆内存
C++ new 堆内存

二叉树：一个结点最多只能有两个结点
满二叉树：一个结点要么有结点，要么没有结点，且叶结点全在同一层

满二叉树结点数：(2n次方)-1，其中n为层数
完全二叉树：满二叉树从下往上、从右向左删除结点后的数位完全二叉树

struct nodeList //链表
{
　　int data;
　　nodeList *nextNode;
};

struct node //二叉树
{
　　int data;
　　node* pLChild;
　　node* pRChild;
};

针对完全二叉树可以使用数组来盛放每个结点(完全二叉树的优势)
假设根结点下标为0开始
已知父结点下标为n，则左子结点的下标为2n+1
已知父结点下标为n，则右子结点的下标为2n+2
已知左子结点下标为m，则父结点的下标为(m-1)/2
已知右子结点下标为m，则父结点的下标为(m-2)/2

如果m=1,则其父结点下标为(1-1)/2=0
如果m=2,则其父结点下标为(2-1)/2=0
即在计算机中(m-1)/2=(m-2)/2
int型变量相除只看个位

堆：有序的完全二叉树，但是这个有序只是限定父子之间有序
01)最大堆(大顶堆)：父结点中存的数大于子结点中存的数
02)最下堆(小顶堆)：父结点中存的数小于子结点中存的数
所以堆即是完全二叉树也是一个数组，因为完全二叉树可以使用数组表示方便

堆排序原理：

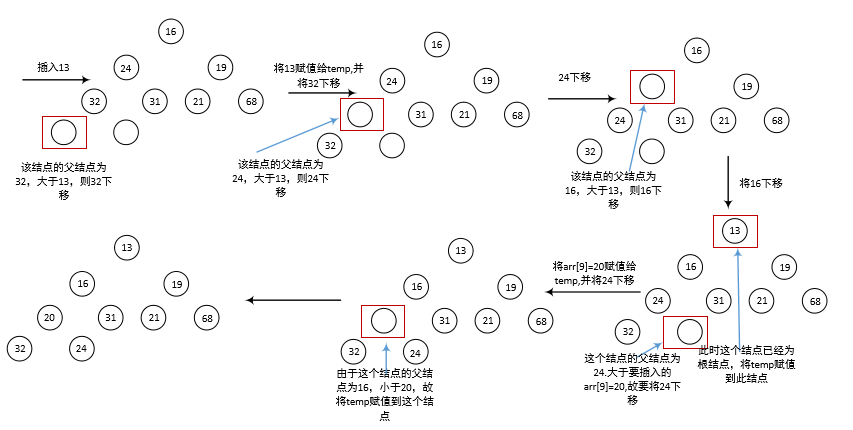
以下是使用类模板方法实现堆，因此在该h文件中对函数做了实现

#pragma once

#include <iostream>

using namespace std;

template <class T>
class MyHeap
{
    T* pBuff;  //数组首地址
    size_t size;  //堆元素个数
    size_t maxSize;  //堆容量
public:
    MyHeap()
    {
        pBuff = NULL;
        size = 0;
        maxSize = 0;
    }
    ~MyHeap()
    {
        if (pBuff)
            delete pBuff;
        size = maxSize = 0;
    }
    //1、一个一个元素插入到堆中
    void insertDataToHeap(const T & data);
    //2、删除堆顶元素
    //3、用数组来初始化堆
    //4、打印数组中的元素
    void _travel();
private:

};

//1、一个一个元素插入到堆中(实现小顶堆)
template <class T>
void MyHeap<T>::insertDataToHeap(const T & data)
{
    //1.1使用完全二叉树的方式插入,即数组挨个赋值
    if (maxSize <= size)  //如果当前数组中元素个数大于数组容量
    {
        //新开内存是原内存的1.5倍或者是原内存加1
        //maxSize >> 1等价于maxSize=maxSize*1.5
        maxSize = maxSize + (((maxSize >> 1) > 1) ? (maxSize >> 1) : 1);

        T* pTemp = new T[maxSize];  //开内存
        if (pBuff != NULL)  //如果原来有内存,将原来内存数据拷贝到新内存中
        {
            memcpy(pTemp, pBuff, sizeof(T)*size); //将原pBuff中的数据拷贝到pTemp中，拷贝sizeof(T)*size个字节
            delete[] pBuff;  //释放pBuff            
        }
        pBuff = pTemp;    //将pBuff重新指向pTemp指向的内存,pBuff指向的内存消失,但是pBuff指针还是存在的    
    }
    pBuff[size++] = data;  //将数字插入数组

    //1.2检查父是否小于子  这一步在第四步中有对应的代码

    //1.3临时存储插入数据
    T temp = data;
    int currendIndex = size - 1;  //加入当前有五个元素,那么最后的元素下标为4
    int parentIndex;              //当前父结点下标
    //1.4循环比较当前位置a和其父结点b位置是否满足父小于子
         //如果满足或b没有父了则循环结束，否则让结点b位置的数字替代a结点中的数字
         //注：a结点是位置放的是要插入的数字
    //当前下标为0则循环结束
    while (currendIndex)
    {
        parentIndex = (currendIndex - 1) / 2;  //在计算机中(currendIndex-1)/2=(currendIndex-2)/2，所以不用分currendIndex是左结点下标还是右结点下标
        if (pBuff[parentIndex] > temp)  //如果当前结点的父节点大于要插入的数，则冲突
        {
            pBuff[currendIndex] = pBuff[parentIndex];  //用当前节结点的父结点替代当前结点中的数
        }
        else
        {
            break;  //如果不冲突跳出循环

        }
        currendIndex = parentIndex;  //下标向上移动
    }
    //1.5临时存储的新插入数据覆盖当前位置
    pBuff[currendIndex] = temp;
    //_travel();  //打印数据
}

//4、打印数组中的元素
template <class T>
void MyHeap<T>::_travel()
{
    cout << "heap:";
    for (int i = 0; i < size; i++)
        cout << pBuff[i] << " ";
    cout << endl;
}

测试用代码:

#include <iostream>
#include "MyHeap.h"

using namespace std;

int main()
{
    MyHeap<int> heap;
    int arr[] = { 32,21,16,24,31,19,68,13,20 };
    for(int i=0;i<sizeof(arr)/sizeof(arr[0]);i++)
        heap.insertDataToHeap(arr[i]);
    heap._travel();
    
    system("pause");
    return 0;
}

测试结果：

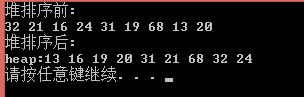
 2、删除堆顶元素，即删除堆中最小元素

      删除堆顶元素后，需要补一个元素进来，那么就首先考虑堆数组中的最后一个元素lastData，但是也不知直接将堆数组中最后一个元素直接赋值
到堆顶，而是先将lastData存起来。然后进行如下的判断：如果lastData大于堆顶元素左结点和右结点中较小的一个结点值，说明当前堆顶不可以放
lastData,可以将(堆顶元素左结点和右结点中较小的一个结点值)放在堆顶，然后继续判断(堆顶元素左结点和右结点中较小的一个结点)的左右结点和lastData
的大小关系，直到找到lastData小于(当前结点i的左右结点较小的一个值),那么结点i就是lastData要存放的地址。

 

 

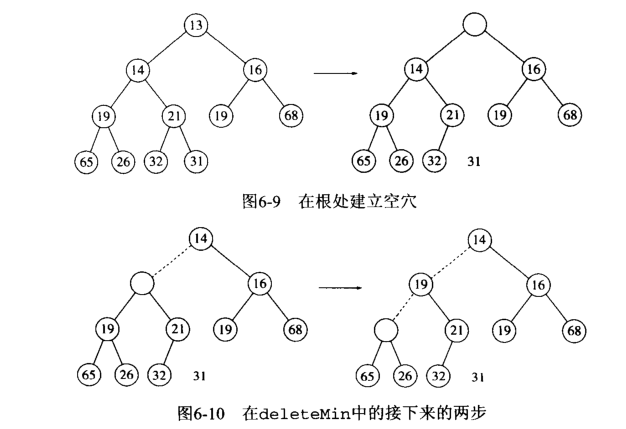
 实现及测试代码：

#pragma once

#include <iostream>

using namespace std;

template <class T>
class MyHeap
{
    T* pBuff;  //数组首地址
    size_t size;  //堆元素个数
    size_t maxSize;  //堆容量
public:
    MyHeap()
    {
        pBuff = NULL;
        size = 0;
        maxSize = 0;
    }
    ~MyHeap()
    {
        if (pBuff)
            delete pBuff;
        size = maxSize = 0;
    }
    //1、一个一个元素插入到堆中
    void insertDataToHeap(const T & data);
    //2、删除堆顶元素
    T deleteMinData();  
    //3、用数组来初始化堆
    //4、打印数组中的元素
    void _travel();
private:

};

//1、一个一个元素插入到堆中(实现小顶堆)
template <class T>
void MyHeap<T>::insertDataToHeap(const T & data)
{
    //1.1使用完全二叉树的方式插入,即数组挨个赋值
    if (maxSize <= size)  //如果当前数组中元素个数大于数组容量
    {
        //新开内存是原内存的1.5倍或者是原内存加1
        //maxSize >> 1等价于maxSize=maxSize*1.5
        maxSize = maxSize + (((maxSize >> 1) > 1) ? (maxSize >> 1) : 1);

        T* pTemp = new T[maxSize];  //开内存
        if (pBuff != NULL)  //如果原来有内存,将原来内存数据拷贝到新内存中
        {
            memcpy(pTemp, pBuff, sizeof(T)*size); //将原pBuff中的数据拷贝到pTemp中，拷贝sizeof(T)*size个字节
            delete[] pBuff;  //释放pBuff            
        }
        pBuff = pTemp;    //将pBuff重新指向pTemp指向的内存,pBuff指向的内存消失,但是pBuff指针还是存在的    
    }
    pBuff[size++] = data;  //将数字插入数组

    //1.2检查父是否小于子  这一步在第四步中有对应的代码

    //1.3临时存储插入数据
    T temp = data;
    int currendIndex = size - 1;  //加入当前有五个元素,那么最后的元素下标为4
    int parentIndex;              //当前父结点下标
    //1.4循环比较当前位置a和其父结点b位置是否满足父小于子
         //如果满足或b没有父了则循环结束，否则让结点b位置的数字替代a结点中的数字
         //注：a结点是位置放的是要插入的数字
    //当前下标为0则循环结束
    while (currendIndex)
    {
        parentIndex = (currendIndex - 1) / 2;  //在计算机中(currendIndex-1)/2=(currendIndex-2)/2，所以不用分currendIndex是左结点下标还是右结点下标
        if (pBuff[parentIndex] > temp)  //如果当前结点的父节点大于要插入的数，则冲突
        {
            pBuff[currendIndex] = pBuff[parentIndex];  //用当前节结点的父结点替代当前结点中的数
        }
        else
        {
            break;  //如果不冲突跳出循环
        }
        currendIndex = parentIndex;  //下标向上移动
    }
    //1.5临时存储的新插入数据覆盖当前位置
    pBuff[currendIndex] = temp;
    //_travel();  //打印数据
}

template <class T>
T MyHeap<T>::deleteMinData()
{
    if (size == 0)
        return 0;
    T minData = pBuff[0];  //保存栈顶即最小元素
    //T lastData = pBuff[size--];  //刚才这一句写成这个样子导致lastData没有值,这是因为数组中一共有size个数，最后一个数的下标是size-1
    T lastData = pBuff[--size];  //将堆中最后一个元素赋值给lastData后，size自减1，这是由于删除堆顶元素后，堆数组内元素减少1
    int currnetIndex = 0;  //当前元素(栈顶元素)的下标，即0
    int i, child;          //child为结点i的左结点或右结点
    for (i = currnetIndex; 2 * i + 1 < size; i = child)
    {
        child = 2 * i + 1;  //设置child为结点i的左结点
        if (child != size && pBuff[child] > pBuff[child + 1])
            child++;    //如果当前结点的右结点小于左结点,那么让child成为右结点
        if (pBuff[child] < lastData)
            pBuff[i] = pBuff[child];  //如果堆数组中最后一个元素大于当前节点i左结点或者是右结点中较小的一个数字,那么说明需要将左结点或者是右结点中较小的一个数字填充在当前节点i上
        else
            break;                    //否则说明数组中最后一个元素比当前节点i左结点或者是右结点中较小的一个数字还要小，那么当前结点的索引i就是要存放lastData的地方
    }  //执行完for循环后，就找到了一个结点i来存放lastData
    pBuff[i] = lastData;

    return minData;
}

//4、打印数组中的元素
template <class T>
void MyHeap<T>::_travel()
{
    cout << "heap:";
    for (int i = 0; i < size; i++)
        cout << pBuff[i] << " ";
    cout << endl;
}

//删除堆顶元素，即删除堆中最小元素
//删除堆顶元素后，需要补一个元素进来，那么就首先考虑堆数组中的最后一个元素lastData，但是也不知直接将堆数组中最后一个元素直接赋值
//到堆顶，而是先将lastData存起来。然后进行如下的判断：如果lastData大于堆顶元素左结点和右结点中较小的一个结点值，说明当前堆顶不可以放
//lastData,可以将(堆顶元素左结点和右结点中较小的一个结点值)放在堆顶，然后继续判断(堆顶元素左结点和右结点中较小的一个结点)的左右结点和lastData
//的大小关系，直到找到lastData小于(当前结点i的左右结点较小的一个值),那么结点i就是lastData要存放的地址。

#include <iostream>
#include "MyHeap.h"

using namespace std;

int main()
{
    MyHeap<int> heap;
    int arr[] = { 32,21,16,24,31,19,68,13,20 };
    cout << "堆排序前: \n";
    for (int i = 0; i < 9;i++)
        cout << arr[i] << " ";
    cout << "\n堆排序后:\n";
    for(int i=0;i<sizeof(arr)/sizeof(arr[0]);i++)
        heap.insertDataToHeap(arr[i]);
    heap._travel();
    int temp = heap.deleteMinData();  //删除堆顶元素
    cout << "删除堆顶元素后:\n";
    heap._travel();
    
    system("pause");
    return 0;
}

测试结果：

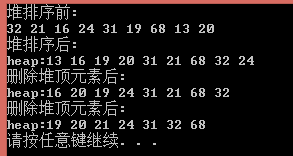
 3、总结

/*
总结(堆数组的插入和删除，以小顶堆为例)
01)堆数组插入一个元素(实际上执行的是堆中新开辟的一个结点执行上滤的操作)
   堆数组插入一个元素是将要堆中新开辟的一个结点执行上滤操作。假如要插入的数据为data,首先将该数据放在一个临时存储区temp,然后
   然后找到堆中最后一个结点的父结点(结点1)，加入结点1的数据大于temp,那么将结点1移动到堆中最后一个结点；然后比较结点1的
   父结点(结点2)和temp的大小，假如结点2中的数据大于temp，则将结点2赋值到结点1，以此类推，直到找到一个结点i，结点i的父
   结点小于temp,将temp赋值到结点i；
02)堆数组删一个元素(实际上执行的是堆顶结点执行下滤的操作)
   堆顶元素被删除，那么我们可以选择堆数组中最后一个元素来弥补这个空缺的位置，但并不是直接将堆数组最后一个元素插入到堆顶就完了。
   假如堆中最后一个元素比堆顶结点的左右结点中较小的一个数还要小，那么就将堆中最后一个元素放在堆顶；
   假如堆中最后一个元素比堆顶结点的左右结点中较小的一个数还要大，那么将顶结点的左右结点中较小的一个数插入到堆顶，假如是左结点较小
   那么再比较该左结点的左右结点和temp的大小，直到找到一个结点i，最后一个元素比结点i的左右结点中较小的一个数还要小，那么我们就将堆
   中最后一个元素放在结点i。
*/

16、二分法

1、二分法查找简答实现

//二分法查找简答实现
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main()
{
    vector<int> value = { 24,56,72,49,15,37,28,57,83,12,32,20,18 };
    int target = 56;
    sort(value.begin(), value.end());  //将数组value进行从小到大排序
    for (int i = 0; i < value.size(); i++)
        cout << value[i] << " ";
    cout << endl;
    int i = 0;
    int j = value.size() - 1;
    while (i <= j)
    {
        int mid = (i + j) / 2;   //找出中间的Index
        if (value[mid] < target)
            i = mid + 1;
        else if (value[mid] > target)
            j = mid - 1;
        else if (value[mid] == target)
        {
            cout << mid << endl;
            system("pause");
            return value[mid];
        }
    }

    system("pause");
    return 0;
}

执行结果：

 2、实例：求f(x) = x ^ 3 - x - 1在[1，1.5]内的一个实根，使误差不超过0.005。

//实例：
//求f(x) = x ^ 3 - x - 1在[1，1.5]内的一个实根，使误差不超过0.005。
#include <iostream>
#include <math.h>

using namespace std;

float getValue(float & x)
{
    return x * x*x - x - 1;
}

int main()
{
    float error = 0.0005f;  //加f是为了防止"“初始化”: 从“double”到“float”截断"警告
    float low = 1.0f;
    float high = 1.5f;
    float middle=0.0f;  //小数点后9个数字
    double test = 1.8;  //小数点后16个数字

    while (fabs((high-low))>=error)                 //区间缩小在error内，则解一定是在这个区间内了
    {
        middle = (low + high) / 2;
        if ((getValue(middle)*getValue(low)) < 0)  //说明在区间[low,middle]内有解,则缩小区间让high=middle
            high = middle;
        else
            low = middle;
    }
    cout << "该方程的解是：" << middle << endl;

    system("pause");
    return 0;
}

运行结果：

3、远亲不如紧邻笔试题---使用二分法实现

题目：链接为：https://www.nowcoder.com/practice/1b2c9a2ba11746958036b29f2e9ee72b?tpId=110&&tqId=33454&rp=1&ru=/activity/oj&qru=/ta/job-code/question-ranking

1)自己先写的(有缺陷，在二分法子函数那里)

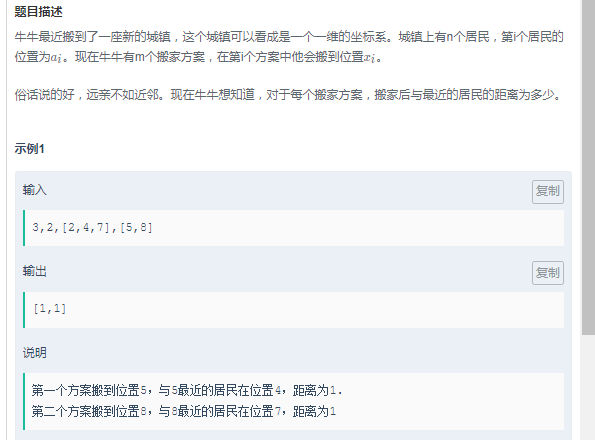
class Solution {
public:
    /**
     * 远亲不如近邻
     * @param n int整型 居民个数
     * @param m int整型 方案个数
     * @param a int整型vector 居民的位置
     * @param x int整型vector 方案对应的位置
     * @return int整型vector
     */
    //其中n为居民个数(邻居个数),数组a为邻居的位置,target为居住方案对应的位置之一
    int TwoDivid(int n,vector<int>& a,int target)
    {
        int low=0;
        int high=n-1;
        int middle;
        sort(a.begin(),a.end());
        while(low<high)
        {
            middle=(low+high)/2;
            if(a[middle]<target)
                low=middle+1;
            if(a[middle]>target)
                high=middle-1;            
        }
        return a[middle];
    }
    vector<int> solve(int n, int m, vector<int>& a, vector<int>& x) 
    {
        vector<int> disShortest(m);  //刚刚由于没有给disShortest初始化数据的个数，导致在使用disShortest[j++]报错数组越界
        int j=0;
        for(int i=0;i<m;i++)
        {
            int value=TwoDivid(n,a,x[i]);
            disShortest[j++]=abs((x[i]-value)); 
        }
        return disShortest;
    }
};

2)看来答案之后的修改版

class Solution {
public:
    /**
     * 远亲不如近邻
     * @param n int整型 居民个数
     * @param m int整型 方案个数
     * @param a int整型vector 居民的位置
     * @param x int整型vector 方案对应的位置
     * @return int整型vector
     */
    //其中n为居民个数(邻居个数),数组a为邻居的位置,target为居住方案对应的位置之一
    int TwoDivid(int n,vector<int>& a,int target)
    {
        int low=0;
        int high=n-1;
        int middle;
        int temp=2e9;      //加入一个很大的数字，以便于在第一次取最小值的时候不取该值
        sort(a.begin(),a.end());
        /*
           01)查找a中最小的大于等于target的位置
           02)由于是找最小的大于等于target的位置，那么只需要在[low,middle]区间内招一个位置和target最接近即可
         */
        if(a[0]>target)         //此时a数组是从小到大已经排序好了的，如果a数组中第一个数都比target大，那么就不需要二分查找了
            temp=a[0]-target;
        else
        {
             while(low<high)
            {
                //middle=(low+high)/2;
                 middle=(low+high)>>1;
                if(a[middle]<=target)
                {
                    temp=min(temp,target-a[middle]); //由于是找最小的大于等于target的位置，那么只需要在[low,middle]区间内招一个位置和target最接近即可
                    low=middle+1;
                }
                //if(a[middle]>target)
                 else
                    high=middle-1;               //由于是找最小的大于等于target的位置,那么在[middle,high]区间内没必要再去取最小值     
            }
        }
        
        /*查找a中最大的小于等于target的位置*/
        if(a[n-1]<target)                  //此时a数组是从小到大已经排序好了的，如果a数组中最后一个数都比target小，那么就不需要二分查找了
            temp=min(temp,target-a[n-1]);//min()中的temp是上面的temp结果
        else
        {
            low=0;
            high=n-1;
             while(low<high)
            {
                //middle=(low+high)/2;
                 middle=(low+high)>>1;
                if(a[middle]<target)
                    low=middle+1;
                //if(a[middle]>=target)
                 else
                 {
                     temp=min(temp,a[middle]-target); 
                     high=middle-1;  
                 }          
            }
        }
        return temp;
    }
    vector<int> solve(int n, int m, vector<int>& a, vector<int>& x) 
    {
        vector<int> disShortest(m);  //刚刚由于没有给disShortest初始化数据的个数，导致在使用disShortest[j++]报错数组越界
        int j=0;
        for(int i=0;i<m;i++)
        {
            int value=TwoDivid(n,a,x[i]);
            disShortest[j++]=value; 
        }
        return disShortest;
    }
};

这个通过率为75%，运行时间超时，但是这个和标准答案差不了哪儿了

03)二分法总结

对于二分法，首先要有一个数组，这个数组的大小是已知的，即区间范围[a,b]是已知的,那么令low=a,high=b,并对a数组进行排序
一般使用vector数组,那么排序的方法为sort(a.begin(),a.end())
在循环里面令middle=(low+high)/2;判断target和a[middle]的大小:
01)如果target>a[middle],则说明target在[middle,high]之间,令low=middle+1;
02)如果target<a[middle],则说明target在[low,middle]之间,令high=middle-1;
循环结束的条件为low>high,则进入循环体的条件为low>=high。在不断地循环的同时，也可以找到target和a[middle]的最小值,即
"远亲不如近邻"这道题。

4、移位与乘除法的关系

a=a*4;   可以替换为：a=a<<2;
b=b/4;   可以替换为：b=b>>2;

说明： 
　　除2 = 右移1位 乘2 = 左移1位 
　　除4 = 右移2位 乘4 = 左移2位 
　　除8 = 右移3位 乘8 = 左移3位 

a=a*9 
　　分析a*9可以拆分成a*(8+1)即a*8+a*1, 因此可以改为： a=(a<<3)+a 
a=a*7 
　　分析a*7可以拆分成a*(8-1)即a*8-a*1, 因此可以改为： a=(a<<3)-a 

2、有符号数据类型的移位操作

对于char、short、int、long这些有符号的数据类型：

对负数进行左移：符号位始终为1，其他位左移

对正数进行左移：所有位左移，即 <<，可能会变成负数

对负数进行右移：取绝对值，然后右移，再取相反数

对正数进行右移：所有位右移，即 >>

3、无符号数据类型的移位操作

对于unsigned char、unsigned short、unsigned int、unsigned long这些无符号数据类型：

参考博客：https://blog.csdn.net/newbird105/article/details/45332621

17、使用stringstream类将string类型转换为int、float、double等类型

//使用stringstream类将string类型转换为int、float、double等类型
#include <iostream>
#include <string>
#include <sstream>
#include <vector>

using namespace std;

string value = "12.2354";
string value2 = "154.122";
vector<string> value3 = { "32.11","68.234","123.32","09.56" };


int main()
{
    double v1 = atof("23.1");    //atof(char*)即atof()参数只能是char类型的，这个是c语言中的函数
    cout << v1 << endl;

    stringstream ss(value);
    float v2;
    ss >> v2;
    cout << v2 << endl;

    stringstream ss2(value2);
    int v3;
    ss2 >> v3;
    cout << v3 << endl;

    vector<float> v4(value3.size());    //必须制定v4的大小，否则在使用v4[j++]的时候会报错数组越界
    int j = 0;
    cout << "string类型: ";
    for (int i = 0; i < value3.size(); i++)
    {
        stringstream ss3(value3[i]);
        ss3 >> v4[j++];
        cout << value3[i] << ",";
    }
    cout << endl;
    cout << "float类型(对string类型加1): ";
    for (int i = 0; i < v4.size(); i++)
        cout << v4[i]+1 << ",";
    cout << endl;


    system("pause");
    return 0;
}

运行结果：

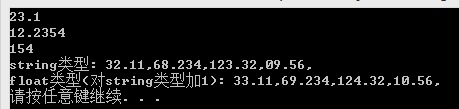
18、归并排序原理和C++实现

 实现原理：采用分治的思想

 

 具体治(合并)的方法为：这里以最长的合并为例

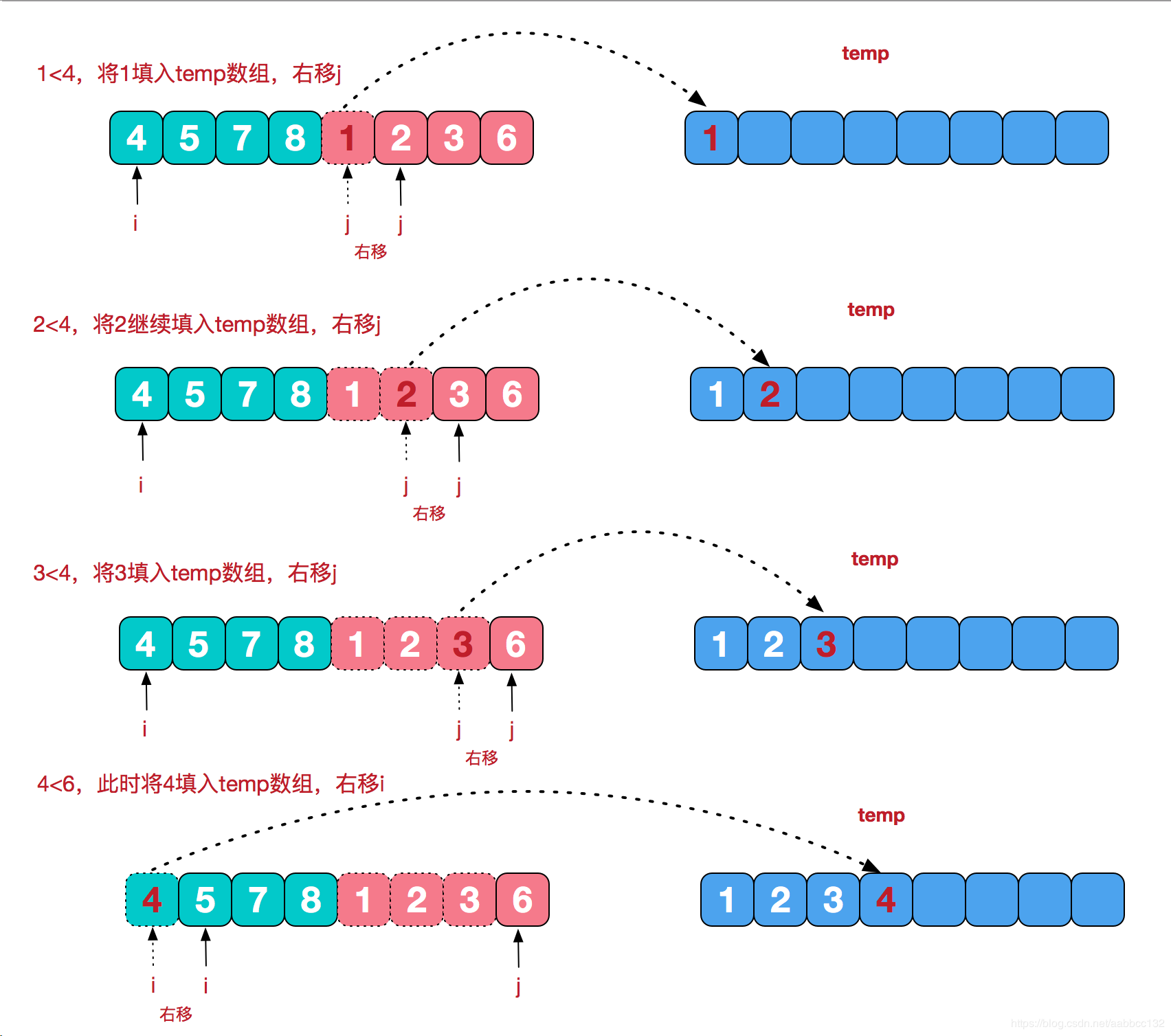
 C++实现：

//归并排序
#include <iostream>

using namespace std;

const int maxn = 9;
int a[maxn] = { 0,8,4,5,7,1,3,6,2 };
int temp[maxn];

void merge(int l, int r, int mid)
{
    int i, j, p;
    i = l;
    j = mid;
    p = l;    //p为temp数组的下标

    while (i < mid && j <= r)  //i<mid表示数组1还有数字,j<=r表示数组2还有数字
    {
        if (a[i] < a[j])
            temp[p++] = a[i++];  //把较小的元素放到temp中去
        else
            temp[p++] = a[j++];  //否则将
    }
    //还有可能i<mid && j<=r只满足一个
    //i<mid表示数组1还有数字，数组2已经没有数字
    while (i < mid)
        temp[p++] = a[i++];
    //j<=r表示数组2还有数字，数组1已经没有数字
    while (j <= r)
        temp[p++] = a[j++];
    p = l; i = l;
    while (p <= r)
        a[i++] = temp[p++];  //将temp数组中的数据copy到a数组中
}

void merge_sort(int l, int r)
{
    if (l < r)
    {
        int mid = (l + r) / 2;
        merge_sort(l, mid);
        merge_sort(mid + 1, r);

        merge(l, r, mid + 1);  //合并，mid+1表示后边那个矩阵的第一个下标
    }
}


int main()
{
    merge_sort(0, 8);
    for (int i = 0; i < maxn; i++)
        cout << a[i] << " ";
    cout << endl;

    system("pause");
    return 0;
}

 19、插入排序

原理即将p指向的元素，向前移动，直到找到一个合适的位置

//插入排序
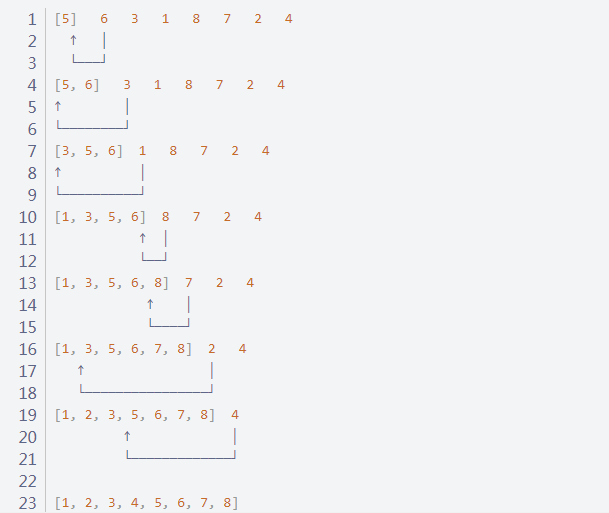
#include <iostream>

using namespace std;

void swap(int & a, int & b)
{
    int temp = a;
    a = b;
    b = temp;
}

//arr为待排序数组,N为数组内元素个数
void insertSort(int* arr, int N)
{
    for (int i = 1; i < N; i++)
    {
        for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--)//如果数组arr中前一个元素arr[i]比后一个元素arr[j+1]大,则交换二者的位置
        {
            swap(arr[j], arr[j + 1]);//相当于将小的值不断的移动到靠前的位置
        }
    }
}

int main()
{
    const int N = 10;
    int arr[N] = { 2,1,4,5,3,8,7,9,0,6 };

    insertSort(arr, N);

    for (int i = 0; i < N; i++)
        cout << arr[i] << " ";
    cout << endl;

    system("pause");
    return 0;
}

插入排序原理，其中N为要排序的数组内元素的个数：

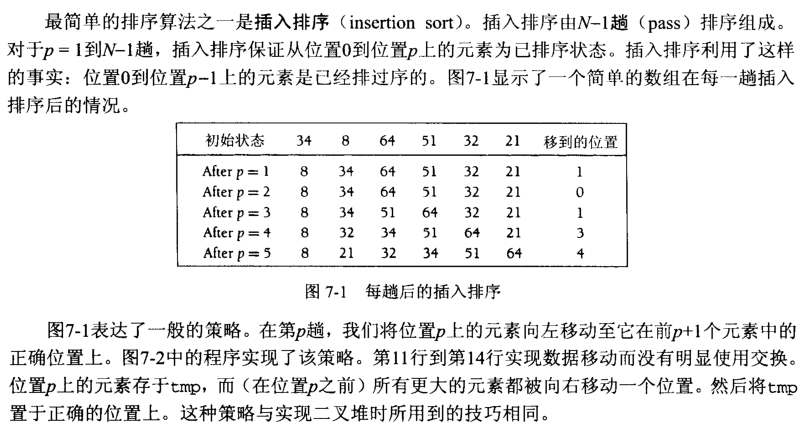
按照上图的思路重新整理的插入排序算法实现：

void insertsort(vector<int>& vec) {
    for (int i = 1; i < vec.size(); ++i) {
        for (int p = i; p > 0 && vec[p] < vec[p - 1]; --p) {
            swap(vec[p], vec[p - 1]);
        }
    }
}

希尔排序(shell排序)m19000

shell排序在不相邻的元素之间比较和交换。利用了插入排序的最佳时间代价特性，它试图将待排序序列变成基本有序的，然后再用插入排序来完成排序工作。

在执行每一次循环时，Shell排序把序列分为互不相连的子序列，并使各个子序列中的元素在整个数组中的间距相同，每个子序列用插入排序进行排序。
举例说明：

以一个整数序列为例来说明{12,45,90,1,34,87,-3,822,23,-222,32}，该组序列包含N=11个数。不少已有的说明中通常举例10个数，这里说明一下，排序算法与序列元素个数无关！ 
首先声明一个参数：增量gap。gap初始值设置为N/2。缩小方式一般为gap=gap/2. 
第一步，gap=N/2=5，每间隔5个元素取一个数，组成一组，一共得到5组：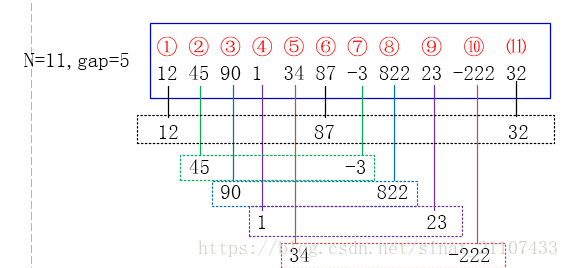 

 

 对每组使用插入排序算法，得到每组的有序数列：

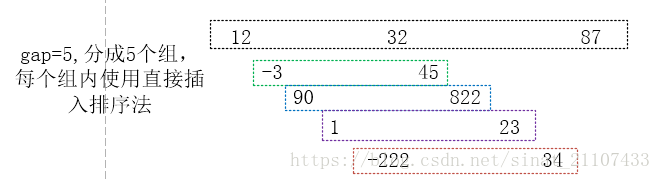
至此，数列已变为：

 

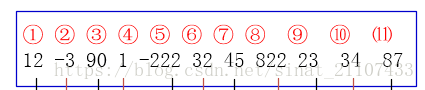
 第二步，缩小gap，gap=gap/2=2，每间隔2取一个数，组成一组，共两组： 

 

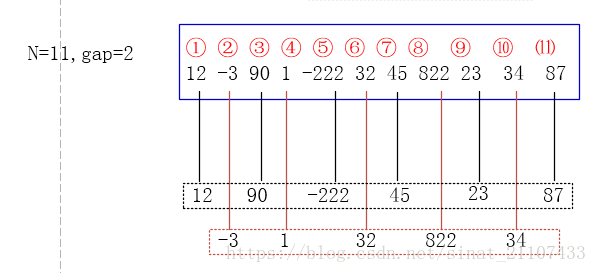
 同理，分别使用插入排序法，得到每组的有序数列： 

 

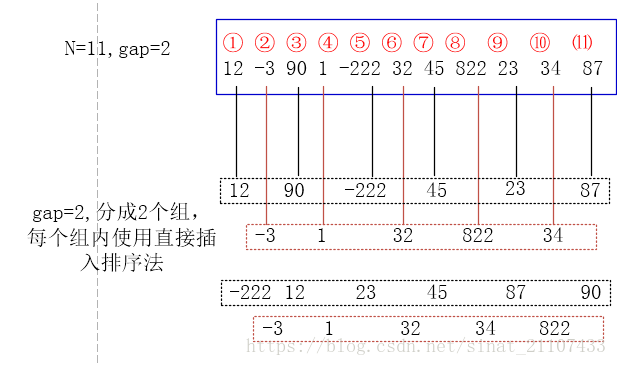
 至此，数列已变为： 

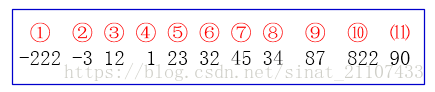
 第三步，进一步缩小gap，gap=gap/2=1，此时只有一组，直接使用插入排序法，玩完成排序，图略。

即shell排序先让一组内的数据有序(也是使用插入排序)，然后再使用插入排序对整组的数据排序 

图片描述：下面的图中一共10个数据，故gap=5

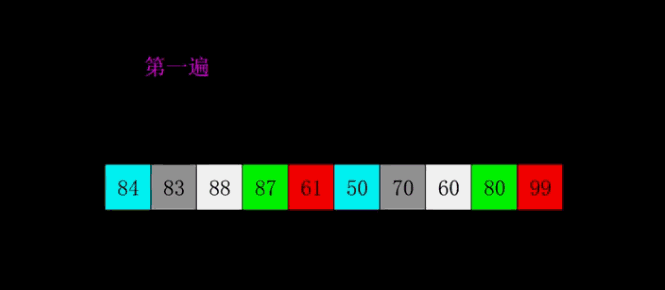
#include <iostream>
#include <vector>
using namespace std;

void shellsort(vector<int> & vec) {
    int gap = vec.size() / 2;
    while (gap >= 1) {
        for (int i = gap; i < vec.size(); ++i) {
            int tmp = vec[i];
            int j;
            for (j = i; j >= gap && tmp < vec[j - gap]; j -= gap)
                vec[j] = vec[j - gap];
            vec[j] = tmp;
        }
        gap /= 2;
    }
}

void insertsort(vector<int>& vec) {
    for (int i = 1; i < vec.size(); ++i) {
        for (int p = i; p > 0 && vec[p] < vec[p - 1]; --p) {
            swap(vec[p], vec[p - 1]);
        }
    }
}

int main() {
    vector<int> vec = { 9,10,5,6,4,7,8,22,0,1,33 };
    shellsort(vec);
    for (int i = 0; i < vec.size(); ++i)
        cout << vec[i] << " ";
    cout << endl;
    
    system("pause");
    return 0;
}

执行结果：

根据自己的理解写的插入排序和shell排序

#include <iostream>
#include <vector>
using namespace std;

void insertSort(vector<int> & vec) {
    for (int i = 1; i < vec.size(); ++i) {
        for (int j = i; j >0 && vec[j]<vec[j-1]; --j) {
            swap(vec[j], vec[j - 1]);
        }
    }
}

void shellSort(vector<int> & vec) {
    int gap = vec.size() / 2;
    while (gap >= 1) {
        for (int i = gap; i < vec.size(); ++i) {
            for (int j = i; j >= gap && vec[j] < vec[j - gap]; j -= gap) {
                swap(vec[j], vec[j - gap]);
            }
        }
        gap /= 2;
    }
}

int main() {

    vector<int> vec = { 23,11,4,46,34,18,90 };
    shellSort(vec);
    for (int i = 0; i < vec.size(); ++i)
        cout << vec[i] << " ";
    cout << endl;

    system("pause");
    return 0;
}

20、单调栈

从名字上就听的出来，单调栈中存放的数据应该是有序的，所以单调栈也分为单调递增栈和单调递减栈

• 单调递增栈：数据出栈的序列为单调递增序列
• 单调递减栈：数据出栈的序列为单调递减序列

ps：这里一定要注意所说的递增递减指的是出栈的顺序，而不是在栈中数据的顺序

现在有一组数10，3，7，4，12。从左到右依次入栈，则如果栈为空或入栈元素值小于栈顶元素值，则入栈；否则，如果入栈则会破坏栈的单调性，则需要把比入栈元素小的元素全部出栈。单调递减的栈反之。

• 10入栈时，栈为空，直接入栈，栈内元素为10。
• 3入栈时，栈顶元素10比3大，则入栈，栈内元素为10，3。
• 7入栈时，栈顶元素3比7小，则栈顶元素出栈，此时栈顶元素为10，比7大，则7入栈，栈内元素为10，7。
• 4入栈时，栈顶元素7比4大，则入栈，栈内元素为10，7，4。
• 12入栈时，栈顶元素4比12小，4出栈，此时栈顶元素为7，仍比12小，栈顶元素7继续出栈，此时栈顶元素为10，仍比12小，10出栈，此时栈为空，12入栈，栈内元素为12。

单调栈的伪代码：

stack<int> st;
//此处一般需要给数组最后添加结束标志符，具体下面例题会有详细讲解
for (遍历这个数组)
{
    while (栈不为空 && 栈顶元素小于当前元素)
    {
        栈顶元素出栈;
        更新结果;
    }
    当前数据入栈;
}

(1)单调栈的应用---逛街

小Q在周末的时候和他的小伙伴来到大城市逛街，一条步行街上有很多高楼，共有n座高楼排成一行。

小Q从第一栋一直走到了最后一栋，小Q从来都没有见到这么多的楼，所以他想知道他在每栋楼的位置处能看到多少栋楼呢？（当前面的楼的高度大于等于后面的楼时，后面的楼将被挡住）

输入描述：

输入第一行将包含一个数字n，代表楼的栋数，接下来的一行将包含n个数字wi(1<=i<=n)，代表每一栋楼的高度。

1<=n<=100000;

1<=wi<=100000; 

输出描述：

输出一行，包含空格分割的n个数字vi，分别代表小Q在第i栋楼时能看到的楼的数量。

示例输入：

6
5 3 8 3 2 5

示例输出：

3 3 5 4 4 4

说明：

当小Q处于位置3时，他可以向前看到位置2,1处的楼，向后看到位置4,6处的楼，加上第3栋楼，共可看到5栋楼。当小Q处于位置4时，他可以向前看到位置3处的楼，向后看到位置5,6处的楼，加上第4栋楼，共可看到4栋楼

#include <iostream>
#include <stack>
#include <vector>
using namespace std;

int main() {
    int n;
    cin >> n;
    int arr[100001];
    stack<int> sta;
    vector<int> left(n);   //保存向左可以看到的楼的个数
    vector<int> right(n);  //保存向右可以看到的楼的个数
    for (int i = 0; i < n; ++i)
        cin >> arr[i];
    //向左看(构建单调递增栈,但实际上在栈中存储的顺序是单调递减的)
    for (int i = 0; i < n; ++i) {
        //left.push_back(sta.size());
        left[i] = sta.size();  //left从0到n-1开始填充数据
        while (!sta.empty() && sta.top() <= arr[i]) {  //如果栈不为空,且当前元素大于栈顶元素
            sta.pop();  //将栈顶元素出栈
        }
        sta.push(arr[i]);
    }
    //清空栈
    while (!sta.empty())
        sta.pop();
    //向右看
    for (int i = n - 1; i >= 0; --i) {
        right[i]=sta.size();
        while (!sta.empty() && sta.top() <= arr[i]) {
            sta.pop();
        }
        sta.push(arr[i]);
    }
    //输出结果
    for (int i = 0; i < n; ++i)
        cout << left[i] + right[i] + 1 << " ";
    system("pause");
    return 0;
}

 题目链接