Multi-target tracking by Lagrangian relaxation to min-cost network flow
Multi-target tracking by Lagrangian relaxation to min-cost network flow
读 “Multi-target tracking by lagrangian relaxation to min-cost network flow, CVPR,2013”小结。
昨晚老板让看一下这篇文章写几句总结给他，所以就看了看，今天顺便简单总结一下这篇文章。
这篇文章模型的核心依然是网络流算法，但和一般网络流算法不同点在于：一般方法在构建图时直接将每一个observation作为node，而observation之间的相互关系使用edge表示，这样每个edge表示的时相连node之间的相似度或者关联程度；而这篇文章所提模型中，在构建图时使用的是candidate pair作为node，然后pair of candidate pairs之间存在这edge，通过这种方式，能够将连续三帧之间的高阶信息，比如连续三帧之间速度近似恒定，融入到模型中。而正是由于不同的构图方式，导致必须引入一些附加的约束以满足多目标跟踪中 track-detection之间的一对一关系。对于提出的模型，通过适当的拉格朗日松弛可以转化为一般的网络流算法有效求解。
illustrative overview of proposed graph representation
使用一个简单的例子清楚的阐述了模型的构图方式。
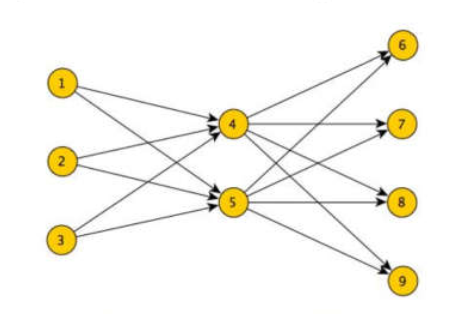
假设现在有连续的三帧图像的observations。第一帧有3个表示为1，2，3，第二帧有两个表示为4，5，第三帧3个表示为6，7，8.一般网络流算法的构图方式如下（这里没有添加源点和汇点）
每条edge的流量是一个二值变量
, 网络流显然应该满足流量守恒约束，每条edge上的代价即相连两个不同帧间observations的匹配程度，然后可以使用最小费用流算法求解模型。上面模型中每条edge上的代价仅仅描述了两帧的相连observations之间的匹配程度，而MTT问题中更高阶的信息往往更加有用。于是作者提出了下面这种构图方式
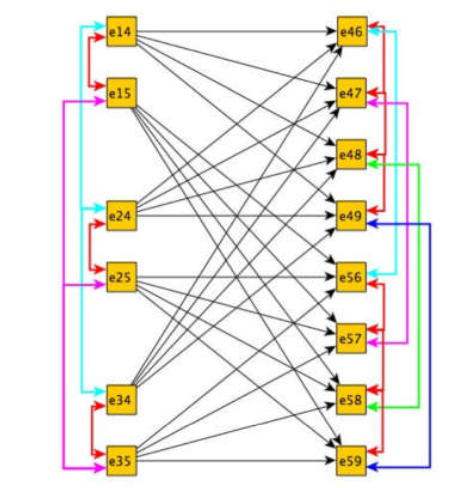
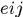表示observations i 和j之间的连接关系，比如
表示observations 1和4之间的连接关系。将连续两帧之间可能存在的匹配作为nodes，比如1，2两帧和2，3两帧的可能匹配都抽象为nodes，然后不同帧间的匹配如果存在公共点，则两个匹配之间存在edge，比如1，2两帧之间的匹配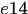
和2，3帧之间的匹配
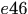之间就存在edge。这样每个edge的cost就是两个匹配之间的相似度，匹配的信息可以包括连接的observations的相对速度和表观差异，这样edge的cost就可以包含相连三帧之间的observations的高阶信息。MTT中一般假设(当然现在好多方法去掉了这个约束)：一条轨迹在任一帧中只能匹配一个observation，同样一个observation只能对应一条轨迹。所以提出的模型中就要对nodes添加额外约束以解决nodes之间的耦合关系，即上图中彩色连线连接的nodes，只能多选一，比如
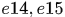，由于两个都经过observation 1，为了满足一一对应约束，必须只能二选一。
problem formulation
形式化表述模型。
现有长度为
的图像序列，第
帧中有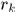
个observations，其集合表示为
, 
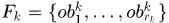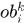表示第k帧的第i个目标。
相邻帧之间可能的匹配对是一个二元组，表示为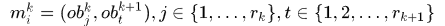
,这些可能的匹配可以由表观相似度，距离相似度等获得。 帧k与k+1之间所有可能的匹配个数表示为
,其集合表示为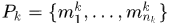
。 那么整个序列中nodes个数为
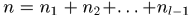,其总的集合表示为
.
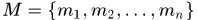由图2进一步细化的图如下：G=(V,E)，其中V包含源点s和汇点t，以及每一个match链接的两个observations，称为incoming node和outgoing node。
.
将每个match表示成两个nodes有两个好处：
1.由于每条边的流量最大为1和流量平衡约束，那么离开outgoing点的流量最多只能为1，因为只有一条进入的link
2.这么做可以将一般网络流算法中unary和binary约束直接添加到match内部的link上，而高阶信息都放在了match与match之间deges上了。
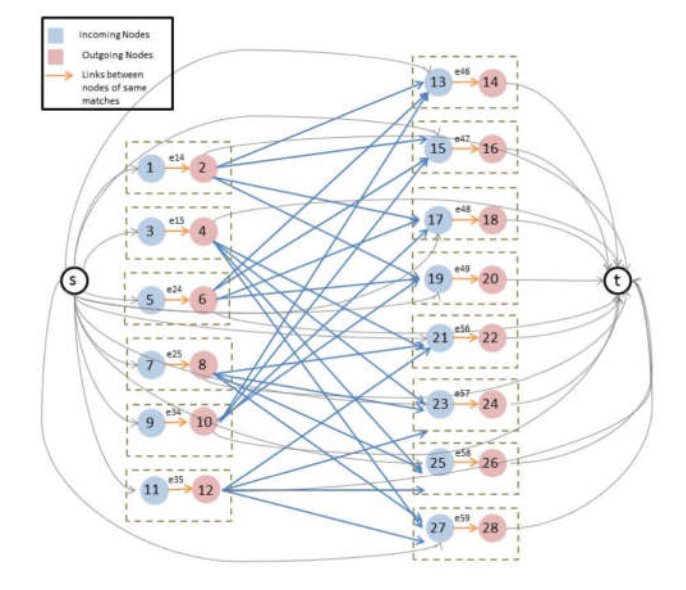
注意这里一直在说连续3帧图像，起始强调3帧只是为了融合高阶信息。像遮挡这种问题就不一定非要是连续帧，通过非连续帧构造类似的图一样可以求解。
整个模型表示如下
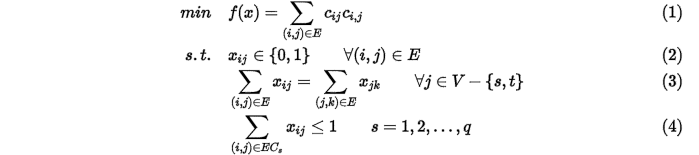
其中
表示边ij的代价，(1)表示最小代价，(2)表示二值约束，(3)表示流量平衡约束，(4)表示附加的用于一一对应的约束。(1)(2)(3)就是一般的网络流算法模型，针对于约束(4),
表示第s个由outgoing和incoming点重合的matches构成的集合，整个序列总共有q个这种集合。
为了求解该模型，将约束(4)通过拉格朗日松弛放到目标式中，然后就可以转换为一般的网络流算法模型进行求解。
其中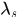
表示拉格朗日乘子
stopping criteria
因为一些约束可能本身过强，始终不可能满足，所以迭代过程可能一直不收敛，这是采用限制最大迭代次数的方式终止算法。
对迭代得到的结果进一步后处理：
连接选中的matches组成tracks
将存在冲突的track拎出来放到一个“competing tracks”的list中
在conflicted tracks中选择lowest cost的track作为正确的track取出
针对于conflicted tracks剩下的tracks，剔除冲突的match看其是否依然能够满足轨迹的条件，比如前后光滑，长度等，满足则创建新的轨迹，不满足就扔掉。
Experiments
文中分别在psu，TUD和ETHMS数据库上进行了实验，具体实验结果参见论文。
conclusion
1.该模型相对于一般的网络流算法使用了更高阶的信息
2.但这里的更高阶也仅仅是3阶的信息，现在有一些利用更高阶信息的方法提出，比基于如张量秩一近似的多目标跟踪。
3.模型通过拉格朗日松弛可以有效的转化为一般的网络流算法求解。
4.针对于算法不收敛的情形，采用了一种贪婪算法作为强制算法结束的补
