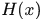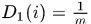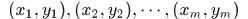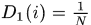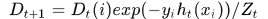AdaBoost 和 Real Adaboost 总结
AdaBoost 和 Real Adaboost 总结
AdaBoost
AdaBoost, Adaptive Boosting(自适应增强), 是一种集成学习算法(ensemble learning),由Yoav Freund 和 Robert Schapire 于1995年提出。其思想是通过多个简单的弱分类器集成一个具有较高准确率的强分类器。
经典AdaBoost算法过程
输入:训练数据
,其中
分别对应着样本特征和样本标签
输出:最终的强分类器
初始化:样本权重分布
循环:t=1,...,T
....-针对权重样本训练弱分类器
....-计算弱分类器的错误率,
是示性函数
....-计算弱分类器的权重
....-使用当前的弱分类器更新样本的分布,其中
是归一化常数
最终的前分类器为:
AdaBoost过程示意图
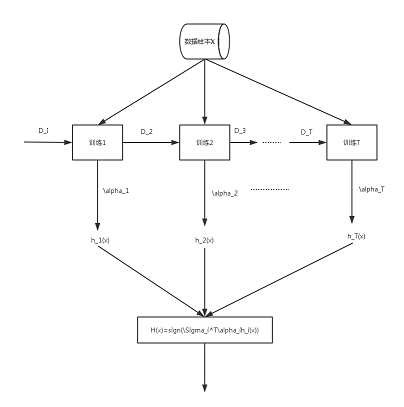
更新迭代原理
从直观上理解,首先,当错误率$\epsilon$越大时,分类器的权重$\alpha$越小,这符合一般解释及分类器性能越高置信度也就越大,在最终的表决中所占比重也就越大。其次,在新样本分布的更新过程中,分类正确的样本在下次分类器学习中作用越小,而分错的样本在下次分类器学习中的作用越大,这样可以是新的分类器设计更集中在之前错分的样本分类上,使整体的分类性能提高。
从理论上推导:
AdaBoost采用的是指数误差函数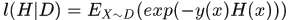 ,其中D是样本的分布,
,其中D是样本的分布, 表示样本的标签,
表示样本的标签,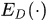 表示在分布D上计算期望。
表示在分布D上计算期望。
i. 首先是权重的更新,希望分类器 产生的总体指数误差最小,则
产生的总体指数误差最小,则

其中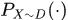 表示某个分布上的概率分布函数。于是得到
表示某个分布上的概率分布函数。于是得到

即分类器权重的更新公式
ii. 接下来将推导分布的更新:
已获得前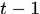 个分类器,我们希望获得第t个分类器能纠 正之前错误分类,使指数误差函数最小。
个分类器,我们希望获得第t个分类器能纠 正之前错误分类,使指数误差函数最小。
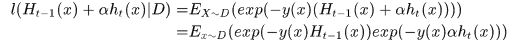
泰勒展开 :
:

这是因为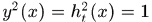

令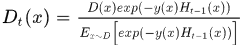 表示一个新的分布,则上式可以写作:
表示一个新的分布,则上式可以写作:
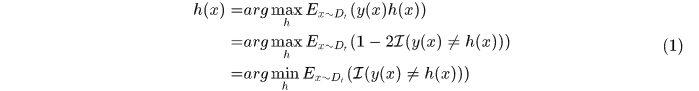
类似的

于是得到分布的更新公式。
AdaBoost的误差上界
在更新分布时有归一化常数

指数误差函数:

AdaBoost分析
虽然在AdaBoost中对弱分类器没有限制,可以是基于多维特征的决策树,SVM等,但通常每个弱分类器都是基于所有特征中某一维构建的,并且输出结果只有+1,-1两种(二分类问题),所以在训练时每一轮迭代相当于挑选最好的特征。
Real AdaBoost
Real AdaBoost 过程:
给定训练集:
训练集样本的初始分布:
循环t=1,2,...,T: (T是弱分类器的个数)
.... - 将每一维特征的取值空间划分为若干个不相交的
.... - 计算在每个子空间上上正负样本的权重

.... - 计算每一个弱分类器的输出,
,其中
是一个很小的正常量用于平滑。
.... - 计算归一化因子
.... - 选择Z最小的的弱分类器作为该轮迭代选出的弱分类器
.... - 更新样本分布
最终的强分类器为:, b是阈值。
Real AdaBoost 的理解
相对于AdaBoost而言,Real AdaBoost中弱分类器不再仅输出{+1,-1},而是输出[-1,1]间的实数,所以称为Real AdaBoost, 我们可以认为输出的值其实就是AdaBoost里的权重加权后的结果,即 ,所以Real AdaBoost也符合AdaBoost的框架
,所以Real AdaBoost也符合AdaBoost的框架
Real AdaBoost 的每个弱分类器设计是一种决策树的简单形式,而每个叶子节点判断依据是将该区间样本分类为样本数最多的那一类。简单的阈值化函数适用于线性可分情况,而对于线性不可分情形,采用这种分区间,即决策树的形式能取得较好的性能。
每次迭代都希望寻找最小分类误差的分类器,而Z值越小表示在对应样本分布下该分类器对应的正负样本个数差别越大,分类结果的置信度越高
下面我们从理论上分析迭代过程:
指数误差函数为:

每次迭代的目标是寻找一个误差最小的分类器,即 最小,那么由AdaBoost框架得到
最小,那么由AdaBoost框架得到
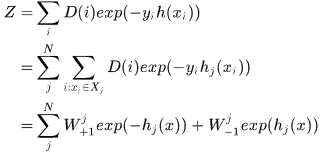
其中 是在该维度上分成N个区间后,落在第j个区间分类器输出值,为了使Z最小,可以得到
是在该维度上分成N个区间后,落在第j个区间分类器输出值,为了使Z最小,可以得到
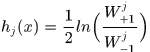
此时Z取得最小值
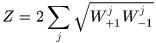
为了使输出函数更加平滑,也为了抑制差距太大或者一方为0的情形,引入平滑因子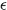 ,一般情况下令
,一般情况下令
Adaboost和Real Adaboost中弱分类器的区别示意图:

matlab实现Real AdaBoost
References:
《机器学习》,周志华著
李志轩,复杂场景中监控视频事件检测算法[D],北京邮电大学,2014