Python数据结构与算法
⭐个人笔记,面向基础,欢迎指正,禁止转载⭐
递归-汉诺塔
查看代码
A = [1,2,3,4] B = [] C = [] def hanoi(n, A, B, C): if n == 1: # 终止条件 C.append(A.pop()) return else: hanoi(n - 1, A, C, B) # 将A经过C移动到B print(n,A,B,C) C.append(A.pop()) # 此时A还剩下最大的盘子,将这个盘子移动到C hanoi(n - 1, B, A, C) # 将B通过A移动到最后一根C hanoi(len(A), A, B, C) # 递归调用 print(A, B, C)
查找算法
列表查找
import time def get_time(f): def inner(*arg,**kwarg): s_time = time.time() res = f(*arg,**kwarg) e_time = time.time() print('耗时:{%.5f}秒' %(e_time - s_time)) return res return inner li = [1,2,3,4,5,96,55,45] #顺序查找,线性查找 def linear_search(list,val): for ind,dest in enumerate(list): if dest== val: return ind else: return None # print(linear_search(li,55))
二分查找
#二分查找,前提是有序 @get_time def dehalf_search(list,val): lt = list.sort() left = 0 right = len(li)-1 while left<=right:#区间内还有候选值 mid = (left+right)//2 #总是向下整取 if list[mid] == val: return mid elif list[mid]>val: right = mid-1 else: #mid<val left = mid+1 print(left, right, mid) else: return None
排序算法
冒泡排序(基础)
import random #冒泡排序,一共会走N-1趟,复杂度n^2 def bubble_sort(arr): for i in range(len(arr)-1): #趟数 counter = False for j in range(len(arr)-i-1):#每一趟需要对比的次数 if arr[j]<arr[j+1]: arr[j],arr[j+1] = arr[j+1],arr[j] counter = True #上一趟没有发生数据交换认为已经排序完成, if counter == False: break; array = [random.randint(0,1000) for i in range(10)] print(array) bubble_sort(array) print(array)
选择排序(基础)
#选择排序:每次取最小的放到新的列表中,时间复杂度O(N*2) def select_sort(arr): print("选择排序:") arr_new = [] #缺点一:多占了内存 for i in range(len(arr)): min_val = min(arr) #缺点二:不是O(1)的操作 arr_new.append(min_val) arr.remove(min_val) #缺点二:不是O(1)的操作,时间复杂度会增加 return arr_new array = [random.randint(0,1000) for i in range(10)] print(array) print(select_sort(array))#原本array里面的值全部被remove #选择排序优化:不新开内存,本组内部进行交换;假设最小值 def select_sort_upgrade(arr): print("选择排序-升级版:") for i in range(len(arr)-1): #第几趟 min_loc = i #假设最小数为无序区的第一个数 for j in range(i+1,len(arr)): if arr[j] < arr[min_loc]: min_loc = j arr[i],arr[min_loc] = arr[min_loc],arr[i] print(arr) array = [random.randint(0,1000) for i in range(10)] print(array) select_sort_upgrade(array) print(array)
插入排序(基础)
#插入排序:类似于打牌中插牌的过程,O(n^2) def insert_sort(arr): print("插入排序:") for i in range(1,len(arr)): #i表示摸到的牌的下标,手里已经有一张 temp = arr[i] j = i-1 #手里的牌的下标 while arr[j]>temp and j>=0: #当j为0的时候代表第一张牌的位置,移动之后就结束 arr[j+1] = arr[j] #手里的牌依次往右挪 j-=1 #把j往左移 arr[j+1] = temp #将抽到的牌插入右移后空出来的位置 array = [random.randint(0,1000) for i in range(10)] print(array) insert_sort(array) print(array)
快速排序(进阶)
import sys #修改递归最大深度,因为当最坏情况时非常容易超出默认的最大递归深度999 sys.setrecursionlimit(100000) # 快速排序:递归,时间复杂度nlog(n),每一层是logn,一共有a层,可以视为n,实际a比n小;最坏的情况是n^2,可以先随机化再排序 def partition(li, left, right): temp = li[left] # 先抽第一张 while left < right: # 判断双指针,递归的结束条件 # 先从后往前 while li[right] >= temp and left < right: # 从后往前找,找比temp小的数,使用left<right来确保当所有数比第一张大时,内存不溢出 right -= 1 # 再往左看一个 li[left] = li[right] # 如果数组内所有的数都比li[left]大或者找到了,把右边的值写到左边 print("右边找完:", li) # 再从前往后 while li[left] <= temp and left < right: # 从前往后找,找比temp大的数,使用left<right来确保当所有数比第一张大时,内存不溢出 left += 1 li[right] = li[left] # 如果数组内所有的数都比li[right]小或者找到了,把左边的值写到右边 print("左边找完:", li) # 执行完后保证左边的全部比temp小,右边全部比temp大,然后继续下一张牌【】这张牌还是第一张 li[left] = temp # 把原来的值写到空白的地方 return left # 返回middle的值 def quick_sort(li, left, right): if left < right: # 至少有两个元素 mid = partition(li, left, right) # 被分成两部分,继续递归调用来排序这两部分 quick_sort(li, left, mid - 1) quick_sort(li, mid+1, right) li = [5, 7, 4, 6, 3, 1, 2, 9, 8] print("快速排序:") quick_sort(li, 0, len(li) - 1) print("找完:", li)
堆排序(进阶)
堆
堆是一种特殊的完全二叉树(不是堆栈的堆,堆栈的堆是动态分配的内存区域)
大根堆:堆中任意节点都比其孩子节点大
小根堆:堆中任意节点都比其孩子节点小
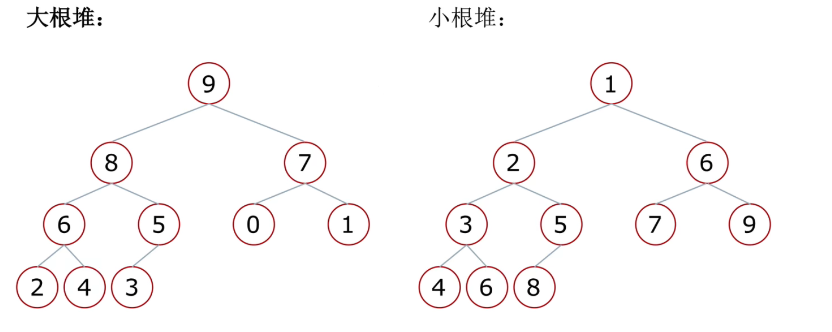
堆的性质:当根节点的左右子树都是堆时,可以通过一次向下调整自动将新元素按照大根堆的性质进行插入
堆排序
# 堆排序:时间复杂度 n*log(n) # 向下调整一次:默认已经是按照大根堆的形式建立了堆 #log(n) def shift(li, Top, Low): # Top:堆顶的位置下标 # Low:最有一个没有检查的位置下标 i = Top # 另存堆顶的下标 j = 2 * i + 1 # 先看左孩子的下标 tmp = li[i] # 另存堆顶 while j <= Low: # 只要孩子节点存在,不超过最后一个节点的下标 if j + 1 <= Low and li[j + 1] > li[j]: # 如果右孩子比左孩子大,并且右孩子存在 j = j + 1 # j放在右孩子上 if li[j] > tmp: li[i] = li[j] # 互换位置 # 更新下标,继续下一层 i = j j = 2 * i + 1 else: # tmp更大 li[i] = tmp # 放到某一级领导的节点上面 break else: # 没有孩子节点了 li[i] = tmp # 放到某一级领导的节点上面 def heap_sort(li): #第一步:利用向下调整建堆,农村包围城市 n = len(li) for i in range(((n-1)-1)//2,-1,-1): shift(li,i,n-1) #建堆完成,挨个出数,先出省长 for i in range(n-1,-1,-1): # i指向当前堆的最后一个位置 li[0] ,li[i] = li[i],li[0] shift(li,0,i-1) #i-1是新的最后元素的下标 #完成 array = [random.randint(0, 100) for i in range(10)] print(array) heap_sort(array) print("堆排序完成",array)
# python内置模块heapq进行堆排序 import heapq import ramdom array = [random.randint(0, 100) for i in range(10)] print(array) heapq.heapify(array)#建堆 for i in range(len(array)): print(heapq.heappop(array),end=',')#每次拿出最小的值,重新存到新列表中就可以了
归并排序(进阶)
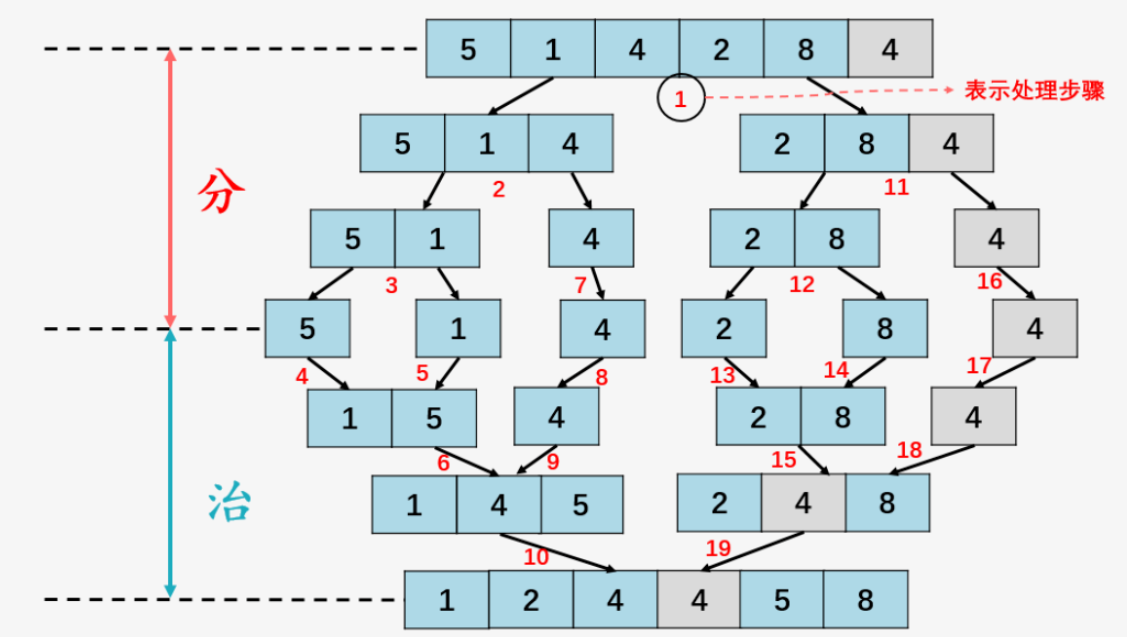
查看代码
# 归并排序:将一个大数组划分为两部分,然后依次进行合并,合并过程中再进行比较排序下,时间复杂度nlog(n):logn层二叉树,每层n # 一次归并:两段列表都是有序的 def merge(li, low, mid, high): i = low # 第一个数下标 j = mid + 1 # 第二个数下标 ltmp = [] # 临时列表 while i <= mid and j <= high: # 左右两边都有数 if li[i] < li[j]: ltmp.append(li[i]) i += 1 # 更新i的下标 else: ltmp.append(li[j]) j += 1 # 更新i的下标 # 执行完后,两部分有一部分没数了,将剩下的继续存到ltmp中 while i <= mid: ltmp.append(li[i]) i += 1 while j <= high: ltmp.append(li[j]) j +=1 # 重新写回 li[low:high + 1] = ltmp # 校验merge li = [2,4,5,7,1,3,6,8] merge(li,0,3,7) print(li) # 递归归并 def merge_sort(li, low, high): if low < high: # 至少有两个数,递归的终止条件 mid = (low + high) // 2 merge_sort(li, low, mid) # 递归左边,直到一个数就是一个分组,然后返回依次归并,归并的过程中排序 merge_sort(li, mid + 1, high) # 递归右边 merge(li, low, mid, high) #合并 array = [random.randint(0, 100) for i in range(10)] print('归并排序', array) merge_sort(array,0,len(array)-1) print('排序完成', array)
排序算法总结
冒泡排序:将紧挨着的两个对比排序
选择排序:每次找最小的一个数放到新的内存中
插入排序:从左到右依次拿出一个数,重新从左往右找第一张比此数大的树位置,放到该位置前面
快速排序:取第一个元素P,使P归位(左边都小,右边都大),递归
堆排序:利用堆的向下归位性质,遍历列表,每次取第i个非叶子节点的元素进行向下归位
归并排序:合并时进行比较按序放到新的数组中,递归
Python数据结构基础
数据结构概述
数据结构是多个对象构成的且对象之间存在一种或多种相互关系的数据集合。程序=数据结构+算法。
线性结构:数据结构中的元素存在一对一的相互关系。比如list、array、dict、set
数据结构:数据结构中的元素存在一对多的相互关系。比如heap
图结构:数据结构中的元素存在多对多的相互关系。
线性结构:列表
概念
列表是一个有序的元素集合列表中的元素是顺序存储的,是一块儿连续的内存:my_list = [1, 2, 3, 'apple', 'banana']
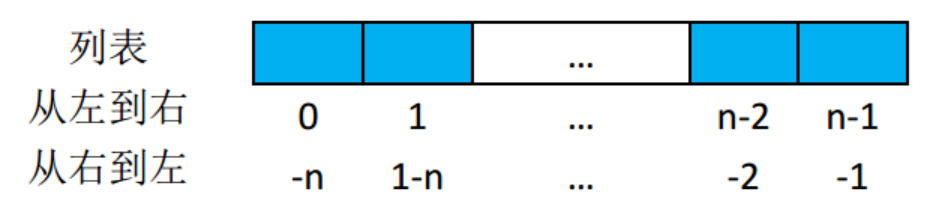
列表操作的时间复杂度
按下标查找:list[x] = O(1)
增加:list.append() = O(1)
插入:list.insert() = O(n)
删除:list.remove() = O(n)
Python列表和C数组的不同
Python列表中元素类型可以不尽相同,C数组的元素成员的数据类型唯一
Python列表长度不唯一,C数组长度唯一
所有的线性结构,本质保存的是数据地址。
P列表和C数组的不同根本在于语言的编译行为不同,Python编译时不需要明确指定成员数据类型和大小。
线性结构:栈
概念
栈是一个数据集合,只能在固定一端进行插入/删除
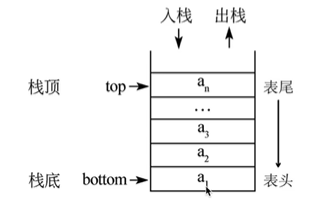
栈特点
LIFO:last-in、first-out
栈操作时间复杂度
进栈:stack.push() = O(1)
出栈:stack.pop() = O(1)
取栈顶:stack.gettop() = O(1)
取栈低:stack.getbottom() = O(n)
栈的实现
列表实现
class Stack: def __init__(self): self.stack = [] def push(self, element): self.stack.append(element) def pop(self): return self.stack.pop() def gettop(self): if len(self.stack) > 0: return self.stack[-1] # 列表的最后一个元素 else: return None def getbottom(self): if len(self.stack) > 0: return self.stack[0] # 列表的第一个元素,这里是利用列表实现的,因此时间复杂度只是O(1) else: return None
线性结构:队列
概念
队列(Quene)是一个数据集合,仅允许从列表的一端插入,另一端进行删除
进行插入的称为队尾,插入动作成为入队
进行删除的一端成为队头,删除动作成为出队

队列特点
FIFO:Fisrt-in,First-Out
队列操作时间复杂度
站在设计角度,队列的时间复杂度应为:
出队:O(1)
入队:O(1)
队列实现
常规顺序列表的操作remove、insert的对象都是值,不是地址,因此时间复杂度都是O(n),不满足入队出队O(1)的时间复杂度要求
因此使用环形队列,插入删除操作使用双指针指向队尾/队首即可:
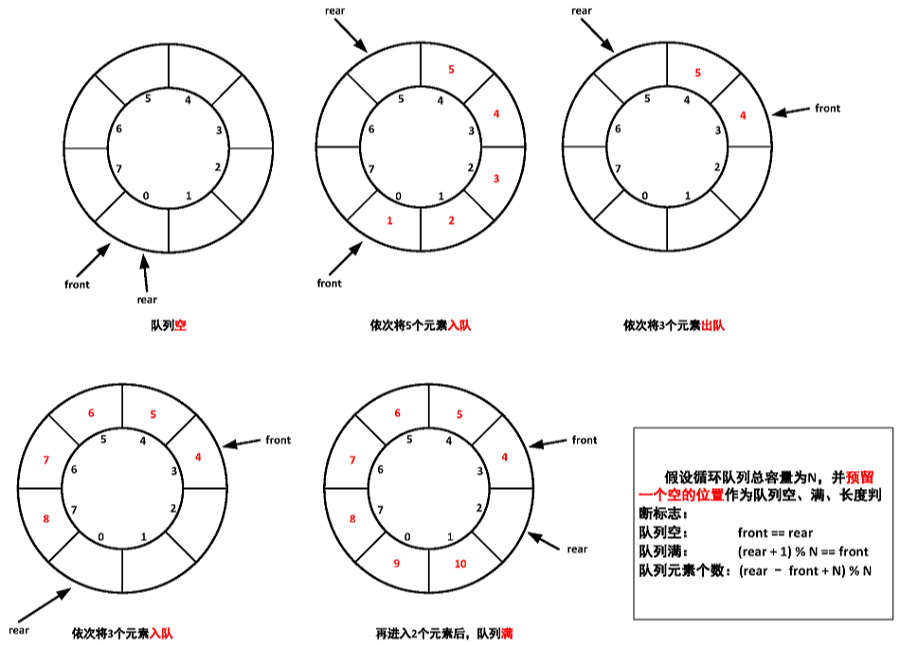
综上,可以得出简单规律:
队空:front = rear
队满:front = (rear + 1)
n个入队后:rear = rear + n
n个出队后:front = front + n
队列元素个数:rear - front
还需要考虑环形时的情况,即rear已经到达了下一圈,front还在上一圈:
总规律:(rear + n + size)% size = front
队空:front = rear
队满:front = (rear + 1) % size
n个入队后:rear = (rear + n) % size
n个出队后:front = (front + n) % size
队列元素个数:(rear - front + size) % size
class Quene: def __init__(self, size=100): self.quene = [0 for _ in range(size)] # 最开始时就必须声明长度 self.rear = 0 # 队尾 self.front = 0 # 队首 self.size = size def push(self, element): if not self.is_full(): self.rear = (self.rear + 1) % self.size self.quene[self.rear] = element else: raise IndexError('Quene is full.') # 抛出错误 def pop(self): if not self.is_empty(): self.front = (self.front + 1) % self.size return self.quene[self.front] else: raise IndexError('Quene is empty.') # 抛出错误 def Size(self): print('quene size = ',(self.rear-self.front + self.size) % self.size) return (self.rear-self.front + self.size) % self.size def is_empty(self): return self.rear == self.front def is_full(self): return (self.rear + 1) % self.size == self.front
双向队列
队列的两端都支持插入与删除
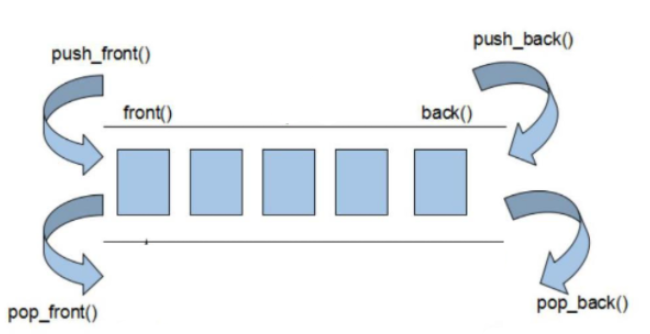
Python的内置队列
Python的内置模块deque是一种支持双向队列的类,因此具备在两端同时入队/出队的操作。一般常用单向队列:
# 队列内置模块 from collections import deque q = deque() # 空队列 # 单向队列操作 q.append(1) # 队尾入队 q.popleft() # 队首出队 # 双向队列操作 q.appendleft(1) # 队首进队 q.pop() # 队尾出队
线性结构:链表
概念
链表是一系列节点组成的元素集合。每个节点都包含本节点信息和指向下一个节点的指针next。最终串联成一个链表。

单链表
单链表实现
头插法
每次从链头插入新节点。
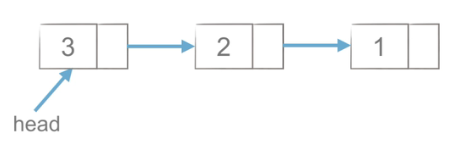
class Node: def __init__(self,item): self.item = item self.next = None def Head_insert(li): head = Node(li[0]) #插入头 for element in li[1:]: node = Node(element) node.next = head head = node return head
尾插法
每次从链尾插入新节点。

class Node: def __init__(self,item): self.item = item self.next = None def Tail_insert(li): head = Node(li[0]) tail = head #每一个尾看做一个头 for element in li[1:]: node = Node(element) tail.next = node tail = node return head
单链表操作
插入:O(1)
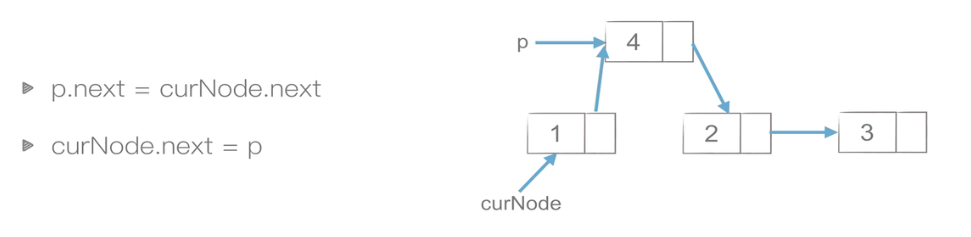
删除:O(1)
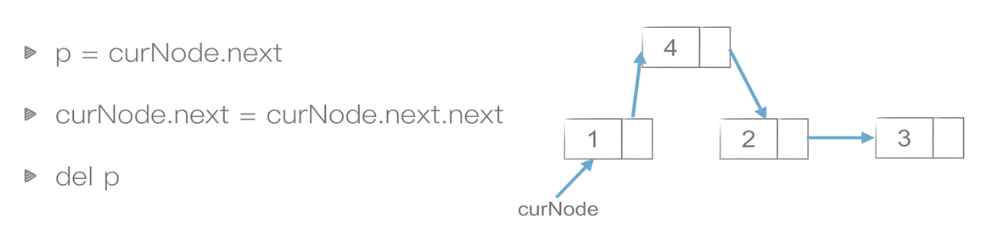
双链表
概念
链表的每个节点有两个指针,分别指向前一个节点和后一个节点。
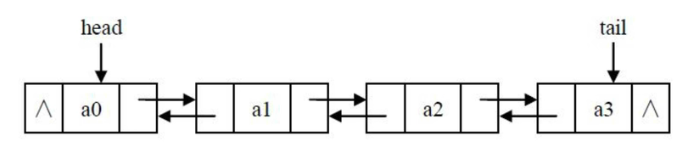
双链表操作
插入:O(1)
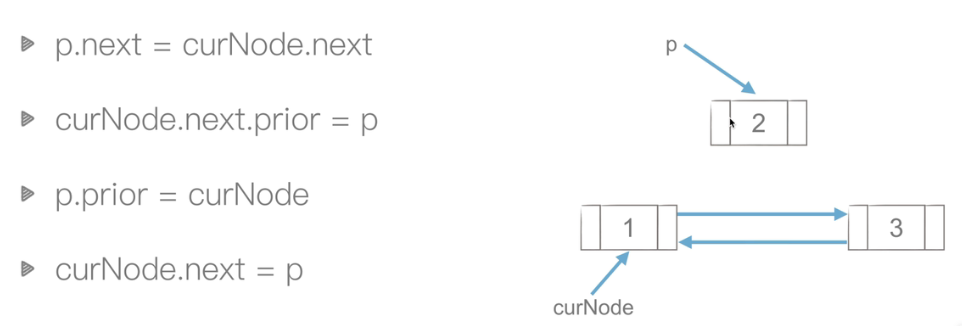
删除:O(1)
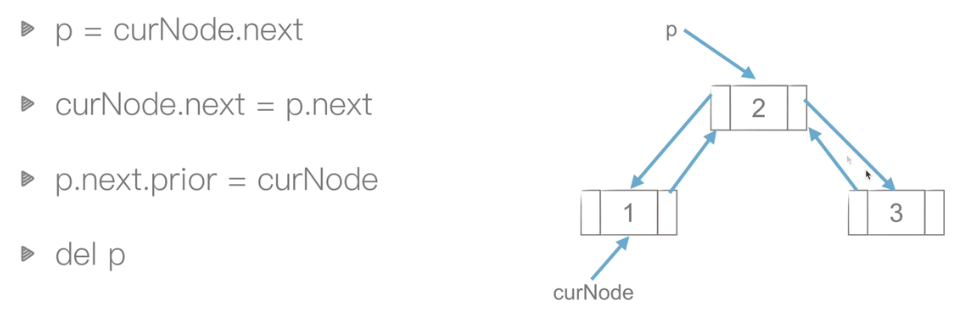
线性结构:哈希表
概念
通过一个哈希函数来计算储存位置的数据结构。
哈希表构成
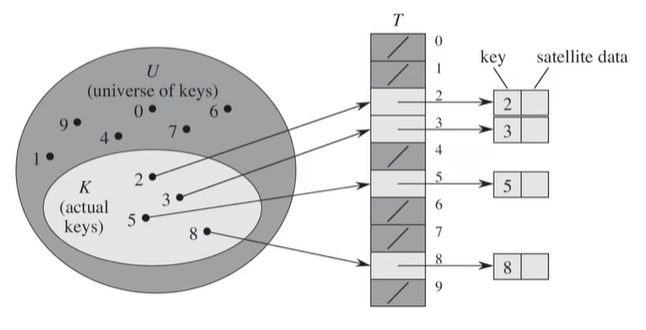
直接寻址表如上图,是一种根据Key查询value的列表T结构。
哈希表是将key作为形参传入一个函数中,通过传入key来计算并返回key在列表T中的下标,此函数为哈希函数。因此查找某一个(key,value)时O(n)时间将随之变大,而传入哈希函数可以直接计算出key的位置,时间复杂度降低为O(1).
哈希表 = 哈希函数 + 直接寻址表T
哈希函数
常规的哈希函数有除法、乘法、全域哈希三种:

哈希冲突
由于哈希函数返回值是有一定规律的,而储存的值的总数量是无限的。因此对于任何哈希函数,都会存在两个key映射到一个value的情况。
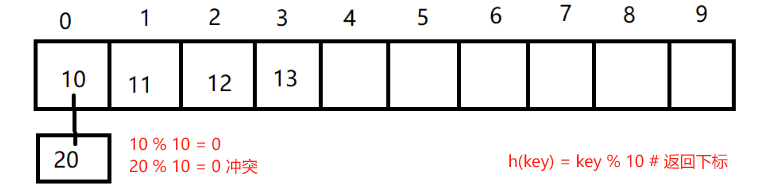
一个哈希函数应尽量把避免这种情况。平均将(key,value)分配到一个位置。所以针对某些特殊场景,也有更加高级的独特的哈希函数来尽量避免哈希冲突。
常见避免哈希冲突的方法有以下两种:
开放寻址法
如果哈希函数的返回的位置已经有值,将探查新的位置来储存这个值。开放寻址法有线性探查、二次探查、二度哈希三种方法来解决哈希冲突。
线性探查:如果位置i被占用,则探查i+1,i+2,...
二次探查:如果位置i被占用,则探查i+1^2,i-1^2,i+2^2,i-2^2,...
二度哈希:有n个哈希函数,如果哈希函数h1发生冲突,则尝试使用h2,h3,...
拉链法
哈希表的每个位置链接一个链表,当冲突发生时,冲突的元素将加到该链表链尾
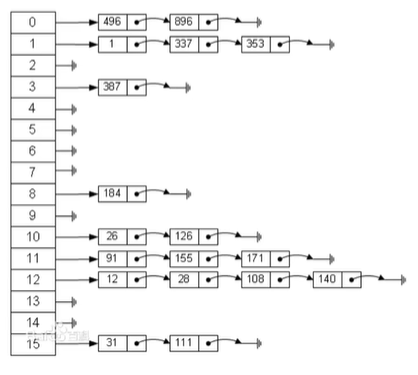
哈希表操作
insert(key,value):插入键值对
get(key):如果存在键为key的键值则返回value,否则返回空值
delete(key):删除键为key的键值对
哈希表因为解决哈希冲突的方法不同,时间复杂度也有不同,这里不做进一步讨论。
python中的字典与集合本质都是哈希表。
拉链法哈希表实现
查看代码
class Linklist: # 定义节点 class Node: def __init__(self, item=None): self.item = item self.next = None # 定义迭代器 class LinkListerIterator: def __init__(self, node): self.node = node def __next__(self): if self.node: cur_node = self.node self.node = cur_node.next # 重新定位下一个节点 return cur_node.item else: raise StopIteration def __iter__(self): return self # 迭代器的返回值必须是可以迭代的对象 def __init__(self, iterable=None): self.head = None self.tail = None if iterable: self.extend(iterable) # 尾插法 def append(self, obj): s = Linklist.Node(obj) if not self.head: self.head = s self.tail = s else: self.tail.next = s self.tail = s # 循环利用尾插法append()将列表保存起来 def extend(self, iterable): for obj in iterable: self.append(obj) # 查找函数 def find(self, obj): for n in self: if n == obj: return True else: return False # 魔术方法:定义迭代器,利用LinkListerIterator类进行迭代 def __iter__(self): return self.LinkListerIterator(self.head) # 魔术方法:重定义输出方式 def __repr__(self): return "<<" + ",".join(map(str, self)) + ">>" class HashTable: def __init__(self, size=101): self.size = size # 定义直接寻址表大小 self.T = [Linklist() for i in range(self.size)] # 开直接寻址表,每个表项填入一个链表类 def h(self, k): return k % self.size # 哈希函数 def insert(self, k): index = self.h(k) # 查找下标 if self.find(k): print("Duplicate insert.") else: self.T[index].append(k) # 成功查找key = k时,返回 value def find(self, k): index = self.h(k) return self.T[index].find(k) # 返回值 hashtable = HashTable() hashtable.insert(0) hashtable.insert(1) hashtable.insert(202) # 会和0在一起 print(",".join(map(str, hashtable.T)))
哈希应用
可知,哈希函数如果恰当的话,一个value的对应key值唯一,因此可以通过md5、SHA2算法(最优)获取两个文件,变量,字符等对象的哈希值来判断文件是否相同。这种相同为尽可能大大大大大的相同,因为当储存的数据无限多时,哈希冲突一定存在。
树与二叉树
树
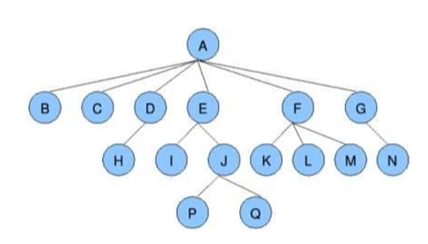
树是一种数据结构,是一种可以递归定义的数据结构
根节点:唯一性;A为根节点
叶子节点:不可分叉的节点,树的末端;B、H、I、P、Q、K、L、M、N为叶子节点
深度:数的最大分叉次数;示例的深度为4
度:数的广度,树的最大宽度;示例为B-C-D-E-F-G,度为6
孩子节点与父节点:描述节点的关系;H为D的孩子节点,D为H的父节点
子树:整树中的一部分;示例中E-I/J就是一个子树
Demo:树状文件系统
查看代码
class Node: def __init__(self, name, type='dir'): self.name = name self.type = type # 'file' or 'dir' self.children = [] # 子节点 self.parent = None # 父节点 def __repr__(self): return self.name class FileSystemTree: def __init__(self): self.root = Node('C:/', 'dir') # 文件系统的根目录 self.now = self.root # 创建文件夹 def mkdir(self, filename): # name必须以/结尾 if filename[-1] != '/': filename += '/' node = Node(filename, 'dir') self.now.children.append(node) # 链接到根目录后 node.parent = self.now # 指定返回路径 # 展示当前目录下的所有目录 def ls(self): return self.now.children # 切换目录,只支持一层 def cd(self,filename): if filename[-1] != '/': filename += '/' if filename == '../': self.now = self.now.parent return for child in self.now.children: if child.name == filename: self.now = child return else: raise ValueError('invalid dir.') tree = FileSystemTree() tree.mkdir('var/') tree.mkdir('bin/') tree.mkdir('user/') print(tree.ls()) tree.cd('bin/') tree.mkdir('python/') print(tree.ls()) tree.cd('../') print(tree.ls())
二叉树
二叉树就是度不超过2的树,也就是每个节点最多有2个孩子节点,称为左孩子节点与右孩子节点
满二叉树:每一层都达到了最大值,也就是生长完全的二叉树
完全二叉树:从满二叉树中的最下排拿走了几个元素的树
非完全二叉树:不是满二叉树和完全二叉树的树
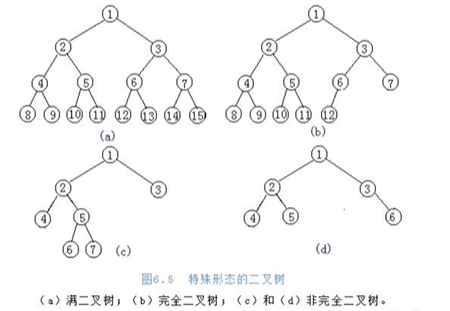
二叉树的存储方式
顺序储存方式:二叉树用列表存,实际是用某种下标关系将列表元素按规律关系想象为一个二叉树

链储存方式:通常用类来保存,类中包含指向上一个节点的指针和指向下一个节点的指针,还有本节点的值。
class BiTreeNode: def __init__(self, data): self.data = data # 节点数据 self.lchild = None # 左孩子节点 self.rchild = None # 右孩子节点
二叉树实现
对于二叉树、任何操作的时间复杂度都是nlogn
A = BiTreeNode('A') B = BiTreeNode('B') C = BiTreeNode('C') D = BiTreeNode('D') E = BiTreeNode('E') F = BiTreeNode('F') G = BiTreeNode('G') E.lchild = A E.rchild = G A.rchild = C C.lchild = B C.rchild = D G.rchild = F ''' E / \ A G \ \ C F / \ B D ''' root = E
遍历

前序遍历
先递归自己、再递归左子树、再递归右子树
前序/后序遍历的第一个一定是根
def pre_order(root): ## 输入根节点 if root: print(root.data,end=',') pre_order(root.lchild) pre_order(root.rchild)

中序遍历
先递归左子树、再递归自己、再递归右子树
def mid_order(root): if root: mid_order(root.lchild) print(root.data,end=',') mid_order(root.rchild)
![]()
后序遍历
先递归左子树、再递归右子树、再递归自己
def post_order(root): if root: post_order(root.lchild) post_order(root.rchild) print(root.data,end=',')

层次遍历
从上往下、从左到右。先遍历第一层、再遍历第二层、第n层......
def layer_order(root): queue = deque() queue.append(root) while len(queue) > 0: # 依次出队 node = queue.popleft() print(node.data, end=',') # 将子节点依次进度完毕 if node.lchild: queue.append(node.lchild) if node.rchild: queue.append(node.rchild)

拓展:二叉搜索树
二叉搜索树是二叉树的一种特殊情况,满足左孩子节点值 ≤ 父节点值 ≤ 右孩子节点值
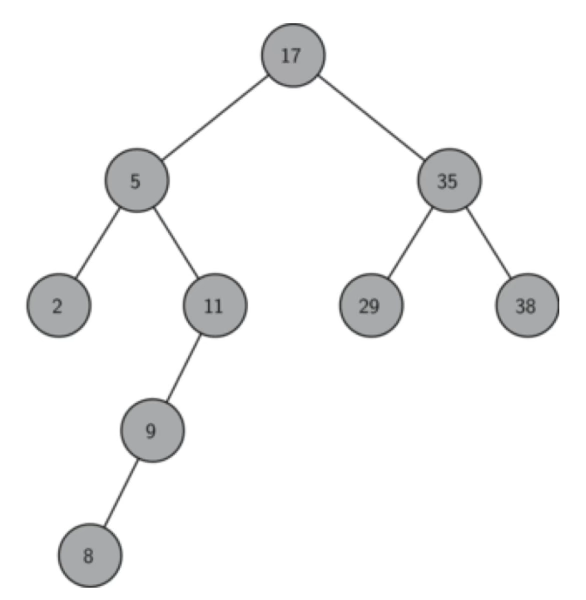
查询
class BiSearchTree: def __init__(self,li = None): self.root = None # 插入传入的列表成员 if li: for val in li: self.insert_no_rec(val) # 查询-递归 def query(self,node,val): if not node: return None if node.data<val: return self.query(node.rchild,val) elif node.data>val: return self.query(node.lchild, val) else: return node # 查询-非递归 def query_no_rec(self,val): p = self.root while p: if p.data < val: p = p.rchild if p.data > val: p = p.lchild else: return p return None
node = tree.query(tree.root,17) print(node.data) node = tree.query_no_rec(17) print(node.data)

插入
class BiSearchTree: def __init__(self,li = None): self.root = None # 插入传入的列表成员 if li: for val in li: self.insert_no_rec(val) def insert_no_rec(self,val): p = self.root if not self.root: # 空树 self.root = BiTreeNode(val) p = self.root return while True: if val < p.data: if p.lchild: p = p.lchild else: # 左孩子不存在 p.lchild = BiTreeNode(val) p.lchild.parent = p print(val,'插入',p.lchild.parent.data,'的左子节点') return elif val > p.data: if p.rchild: p = p.rchild else: # 右孩子不存在 p.rchild = BiTreeNode(val) p.rchild.parent = p print(val,'插入',p.rchild.parent.data,'的右子节点') return else: return def mid_order(self,root): if root: self.mid_order(root.lchild) print(root.data, end=',') self.mid_order(root.rchild)
中序遍历对于搜索二叉树,输出一定是升序的
tree = BiSearchTree([17,5,35,2,11,29,38,9,8]) tree.mid_order(tree.root)

删除
二叉搜索树的删除比较复杂,需要考虑删除非叶子节点时,剩余节点如何重新排布的问题:
情况一:自己就是最下面的子节点/自己就是唯一的根节点
# 情况1:node是叶子节点 def __remove_node_1(self, node): if not node.parent: # 只有一个节点,并且自己就是根节点 self.root = None # 自己不是根节点+清空根节点的子关系 if node == node.parent.lchild: # 自己是父亲的左孩子 node.parent.lchild = None # 隔断联系 else: node.parent.rchild = None # 隔断联系
情况二:自己是父节点,并且是自己父节点的左孩子节点
# 情况21:node是非叶子节点,只有一个左孩子节点 def __remove_node_21(self, node): if not node.parent: # 只有一个节点,并且自己就是根节点 self.root = node.lchild node.lchild.parent = None elif node == node.parent.lchild: # 自己是父亲的左孩子 node.parent.lchild = node.lchild # 自己左孩子变成自己父亲的左孩子 node.lchild.parent = node.parent # 自己左孩子的父亲就是自己的父亲 else: # 自己是父亲的右孩子 node.parent.rchild = node.lchild # 自己左孩子变成自己父亲的右孩子 node.lchild.parent = node.parent # 自己左孩子的父亲就是自己的父亲
情况二:自己是父节点,并且是自己父节点的右孩子节点
def __remove_node_22(self, node): if not node.parent: # 只有一个节点,并且自己就是根节点 self.root = node.rchild node.rchild.parent = None elif node == node.parent.lchild: # 自己是父亲的左孩子 node.parent.lchild = node.rchild # 自己右孩子变成自己父亲的左孩子 node.rchild.parent = node.parent # 自己右孩子的父亲就是自己的父亲 else: # 自己是父亲的右孩子 node.parent.rchild = node.rchild # 自己右孩子变成自己父亲的右孩子 node.rchild.parent = node.parent # 自己右孩子的父亲就是自己的父亲
综合:删除节点后,考虑自己的孩子节点仍是父节点的情况
def delete(self, val): if self.root: node = self.query_no_rec(val) # 找到对应节点 if not node: # 不存在这个数 return False if not node.lchild and not node.rchild: # 没有孩子 self.__remove_node_1(node) elif node.lchild and not node.rchild: # 只有左孩子 self.__remove_node_21(node) elif not node.lchild and node.rchild: # 只有右孩子 self.__remove_node_22(node) else: # 有两个孩子,将其右子树的最小节点删除并替换当前节点 min_node = node.rchild while min_node.lchild: min_node = min_node.lchild # 一直找到最下方的左孩子节点 node.data = min_node.data #替换数据 # 删除节点 if min_node.rchild: self.__remove_node_22(min_node) else: self.__remove_node_1(min_node)
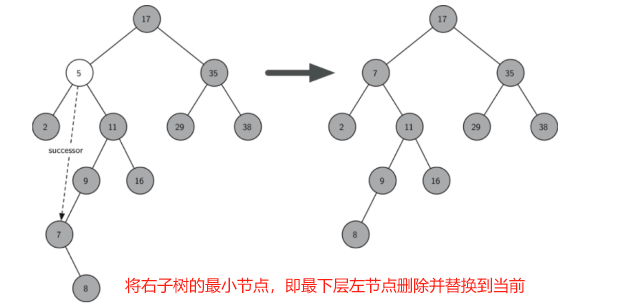
拓展前述:自平衡二叉树
由于二叉树的结构特性,将数据存储到二叉搜索树中,其时间复杂度可以从存储在线性结构的的 O(N) 变成 O(log2 N) 。
但这只是在理想的情况下的效率(如下图左),在实际的操作,树的结构会不断的变换,极端的情况下,可以变为线性结构,时间复杂度近乎于 O(N)。 在数据量非常大情况下,查询速度会非常之低,于是平衡树的概念被提出来了。
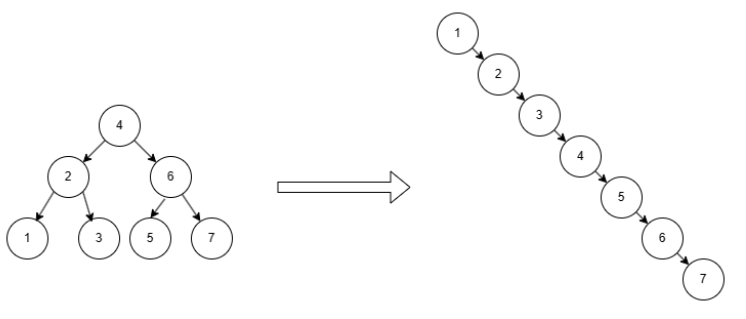
拓展:AVL树
AVL树是一种强平衡的二叉搜索树,要左右子节点的高度差不能大于1,及左右节点各自下方的最长路径差值不能大于1.
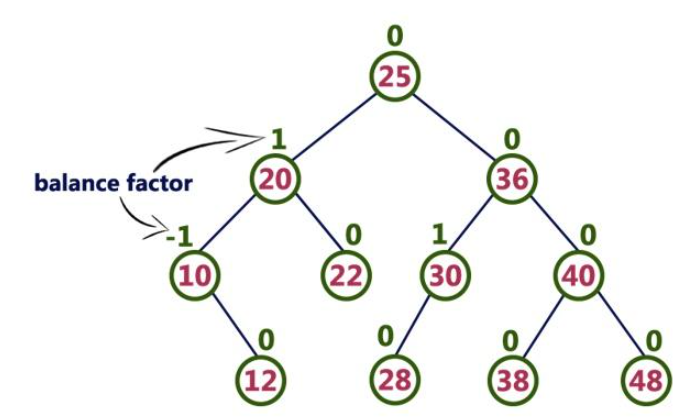
AVL树实现不维护的话,平衡将被打破,因此需要一些特别的操作来维持平衡属性,此为旋转。
不平衡
不平衡一共有四种情况
情况一:不平衡是由于对K的右孩子的右子树插入导致的->左旋
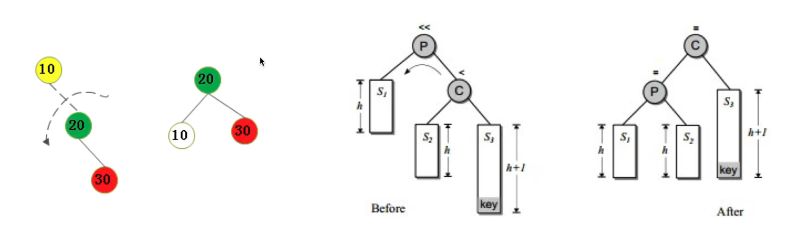
情况二:不平衡是由于对K的左孩子的左子树插入导致的->右旋
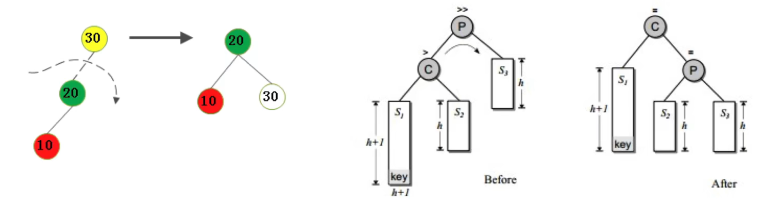
情况三:不平衡是由于对K右孩子的左子树插入导致的->右旋->左旋
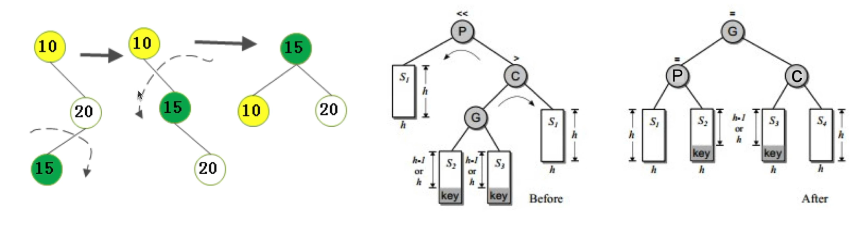
情况四:不平衡是由于对K左孩子的右子树插入导致的->左旋->右旋
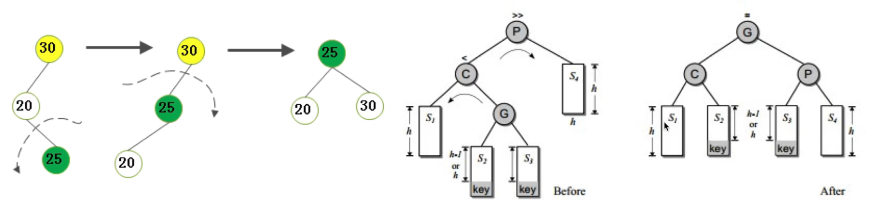
AVL树实现:
查看代码
from 二叉树 import BiTreeNode, BiSearchTree class AVLNode(BiTreeNode): def __init__(self, data): BiTreeNode.__init__(self,data) self.bf = 0 # balanace factor class AVLTree(BiSearchTree): def __init__(self, li=None): BiSearchTree.__init__(self, li) # 情况一 def rotate_left(self, p, c): # s2移到p的右子节点 s2 = c.lchild p.rchild = s2 if s2: s2.parent = p # p移到c的左子节点 c.lchild = p p.parent = c # 更新balance factor p.bf = 0 # p已经平衡 c.bf = 0 # c已经平衡 return c # 情况二 def rotate_right(self, p, c): # s2移到p的左子节点 s2 = c.rchild p.lchild = s2 if s2: s2.parent = p # p移到c的左子节点 c.rchild = p p.parent = c # 更新balance factor p.bf = 0 # p已经平衡 c.bf = 0 # c已经平衡 return c # 情况三 def rotate_right_left(self, p, c): g = c.lchild # 将g的左孩子给p的右孩子节点,,将p挪到g的左孩子节点 s2 = g.lchild p.rchild = s2 if s2: s2.parent = p g.lchild = p p.parent = g # 将g的右孩子给c的左孩子节点,将c挪到g的右孩子节点 s3 = g.rchild c.lchild = s3 if s3: s3.parent = c g.rchild = c c.parent = g # 更新balance factor if g.bf > 0: # # 说明原本S3上有数据,k接着插入到s3 p.bf = -1 c.bf = 0 elif g.bf < 0: # 说明k插到s2 p.bf = 0 c.bf = 1 else: # 插入的是g p.bf = 0 c.bf = 0 g.bf = 0 return g # 情况四 def rotate_left_right(self, p, c): g = c.rchild # 将g的左孩子给c的右孩子节点,,将c挪到g的左孩子节点 s2 = g.lchild c.rchild = s2 if s2: s2.parent = c g.lchild = c c.parent = g # 将g的右孩子给p的左孩子节点,将p挪到g的右孩子节点 s3 = g.rchild p.lchild = s3 if s3: s3.parent = p g.rchild = p p.parent = g # 更新balance factor if g.bf > 0: # 说明k插到s3 p.bf = 0 c.bf = -1 elif g.bf < 0: # 说明k插到s2 p.bf = 1 c.bf = 0 else: # 插入的是g p.bf = 0 c.bf = 0 g.bf = 0 return g # 覆盖父类的方法 def insert_no_rec(self, val): # 和二叉搜索树,先插入 p = self.root if not self.root: # 空树 self.root = AVLNode(val) return while True: if val < p.data: if p.lchild: p = p.lchild else: # 左孩子不存在 p.lchild = AVLNode(val) p.lchild.parent = p node = p.lchild # 保存插入的节点 print(val, 'val插入', p.lchild.parent.data, '的左子节点') break # 结束插入,不能return,因为后续还要旋转 elif val > p.data: if p.rchild: p = p.rchild else: # 右孩子不存在 p.rchild = AVLNode(val) p.rchild.parent = p node = p.rchild # 保存插入的节点 print(val, 'val插入', p.rchild.parent.data, '的右子节点') break else: return # 没有插入可以不调整 # 更新balance factor,从node的parent开始 while node.parent: # node的parent存在 if node.parent.lchild == node: #传递是从左子树来的,左子树更沉了 # 更新node.parent.bf if node.parent.bf < 0: # 看node那边沉,进行旋转 g = node.parent.parent # 为了链接用 x = node.parent # 旋转前的子树的根 if node.bf > 0: print("rotate_left_right") n = self.rotate_left_right(node.parent,node) else: print("rotate_right") n = self.rotate_right(node.parent,node) # 链接g和n elif node.parent.bf > 0:# 原来的是1,插入到了左边,bf不变 node.parent.bf = 0 break else: node.parent.bf = -1 node = node.parent # 继续走循环 continue else: # 从右子树来的,右子树更沉了 if node.parent.bf >0: g = node.parent.parent # 为了链接用 x = node.parent # 旋转前的子树的根 if node.bf < 0: print("rotate_right_left") n = self.rotate_right_left(node.parent, node) else: print("rotate_left") n = self.rotate_left(node.parent, node) # 链接g和n elif node.parent.bf < 0: # 原来的是-1,插入到了右边,bf不变 node.parent.bf = 0 break else: node.parent.bf = 1 node = node.parent # 继续走循环 continue # 链接旋转后的子树,g与n链接起来 n.parent = g if g: if x == g.lchild: g.lchild = n else: g.rchild = n break else: self.root = n break print("------------AVL--------------") tree = AVLTree([9,8,7,6,5,4,3,2,1]) tree.pre_order(tree.root) print("") tree.mid_order(tree.root)
拓展:红黑树
红黑树是一种弱平衡的二叉搜索树,确保最长路径≤2*任意路径。通过给节点打赏红黑颜色标签来判断红黑树是否需要旋转。有兴趣的可以看 最通俗易懂入门红黑树(R-B Tree)-腾讯云开发者社区-腾讯云 (tencent.com)
贪心算法
概念
贪心算法是指,在对问题求解时,总是针对当前情况给出最好的选择。可能不是全局最优解,但一定是局部最优解。
贪心算法的核心是判断贪心算法是否能够用来计算,以及如何贪心?
实例一:找零问题
贪心思想:面值最大的张数最小。
# 找钱问题 # t = [100, 50, 20, 5, 1] def change(t,n): m = [0 for _ in range(len(t))] # 对应的张数 for i,money in enumerate(t): m[i] = n//money #找的张数 n = n % money # 找完还要找多少钱 return m,n print(change([100, 50, 20, 5, 1],376))
![]()
示例二:背包问题

贪心思想:单位最值钱是最先应该拿的。
# 背包问题-分数背包 goods = [(60,10),(100,20),(120,30)] # (价值,重量) goods.sort(key = lambda x: x[0]/x[1],reverse = True) def fractional_package(goods,w): m = [0 for _ in range(len(goods))] # 这是按照排序后的顺序 total = 0 # 拿走的总价值 for i,(prize,weight) in enumerate(goods): if w>=weight: m[i] = 1 # 拿走了全部的 w -= weight total += prize else: m[i] = w/weight w = 0 # 背包被全部占满了 total += m[i]*prize break return m,total print(fractional_package(goods,50))
![]()
示例三:拼接数字最大问题

贪心思想:两两组合分别比较,哪个组合最大就是范围内最优解。
from functools import cmp_to_key li = [32,94,128,1286,6,71] def xy_cmp(x,y): if x+y<y+x: return 1 # y会挪到x前面 elif x+y>y+x: return -1 # y不会挪到x前面 else: return 0 def number_join(li): li_str = list(map(str,li)) li_str.sort(key = cmp_to_key(xy_cmp)) # 升序排序,函数决定要不要转换位置 print(li_str) return ''.join(li_str) #返回列表的拼接,以字符串形式返回 print(number_join(li))

示例四:活动选择问题

贪心思想:最先结束的活动一定是范围内最优解。
from functools import cmp_to_key # (开始时间,结束时间) activities = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 9), (5, 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)] activities.sort(key=lambda x: x[1]) # 按照结束时间进行升序排序 def activitie_selection(a): res = [a[0]] # 最先结束的肯定在里面 # 依次看后面的,没有冲突继续添加 for i in range(1, len(a)): # 当前活动的开始时间大于等于最后一个入选活动的结束时间 # 此时满足条件的一定也是相同开始时间结束最早的,前面已经按照结束时间升序排序 if a[i][0] >= res[-1][1]: res.append(a[i]) # 不冲突,将这个活动添加进来 return res print(activitie_selection(activities))
![]()
动态规划
求解规模为n的问题,可以划分为更小规模的可以独立求解的问题的组合;比较各种组合的解即可得出最优解
斐波那契理解动态规划
F[n]=F[n-1]+F[n-2](n>=2,F[0]=1,F[1]=1)
递归实现
def fibonacci(n): if n == 1 or n ==2: #终止条件 return 1 return fibonacci(n-1)+fibonacci(n-2) #前进
非递归实现(动态规划)
def fibonacci_no_recurision(n): f = [0, 1, 1] if n <= 1: return 1 for i in range(n - 2): num = f[-1] + f[-2] # 每一项都等于前两项之和 f.append(num) return f[-1]
递归实现的斐波那契数列当n=100时,运行时间很长,因为递归的执行效率很低。这个场景下最重要的原因就是子问题的重复计算。因此非递归的思想就是动态规划。
# 递归的重复计算 # f5 = f4 +f3 A操作:计算前两项 # f4 = f3 +f2 A_1操作:A操作中的f4计算前两项 # f3 = f2 +f1 A_2操作:A操作中的f3计算前两项 # f3 = f2 +f1 A_2_1操作:A_2操作中的f3计算前亮相 - 重复计算 # f2 = 1 # ... ...
动态规划的核心:
找出最优子结构:依次递推,动态规划中最难的一点
解决重复子问题:另存子问题结果,不重复计算子
钢条计算问题
问题分析

出售价格与钢条长度之间的关系如上表。现有一段长度为n的钢条,裁剪一次如何裁剪使得收益最大?
1、找出最优子结构:列举出每一种情况下的最优解,后续长度可采用已经求出的长度最优解进行组合

举例长度为6时,6 = 0 + 6 = 1 + 5 = 2 + 4 = 3 + 3
0 + 6 最优解:0 + 17 = 17
1 + 5 最优解:1 + 13 = 14
2 + 4 最优解:5 + 10 = 15
3 + 3 最优解:8 + 8 = 16
即长度为6时,最优解为17。这个过程中我们剔除了4+2、5+1两种,因为重复计算,因此可以看成一边切,一边不切:
最优解 = 切左边最优解(1~n)+剩余右边最优解( n -(1~n)),只需遍历n次即可。
![]()
2、解决重复子问题:依次遍历长度,将每一次求得的最优解保存,下一次直接拿取进行组合
代码实现:最多的钱
# 自顶向下:非动态规划,不保存最优解,直接递归计算 def cut_rod_recurision(p, n): if n == 0: return p[0] else: res = 0 for i in range(1, n+1): # 左边切割,右边不切割。右开导致+1 # 依次比较n的最优值和组合(i+(n-i))= n的最优值那个大,大的返回 res = max(res, p[i] + cut_rod_recurision(p, n - i)) # 递归求解当前n-i的最大值,没有保存 print(i,res) return res print(cut_rod_recurision(price, 7))
# 自底向上:动态规划 def cut_rod_no_recurision(p, n): great = [0] # 保存最优解 for i in range(1, n + 1): res = 0 # 计算i之前所有的最优解 for j in range(1, i + 1): # 遍历所有的组合 res = max(res, p[j] + great[i - j]) great.append(res) # 保存最优解 print(great) return great[n] print(cut_rod_no_recurision(price, 7))
代码重构 :裁剪方案
基于最优的解,我们需要重构来输出最终的裁剪方案。
def cut_solution(p, n): great = [0] # 保存最优解 solution = [0] # 左边的长度 for i in range(1, n + 1): # 计算i之前所有的最优解 maxV = 0 # 价格最大值 leave = 0 # 最大价值时左边不切割的长度 for j in range(1, i + 1): # 遍历所有的组合 if maxV <= (p[j] + great[i - j]): maxV = (p[j] + great[i - j]) leave = j great.append(maxV) # 保存最优解 solution.append(leave) # 保存当前最优解的左边长度 return great[n], (solution[n], n - solution[n]) print(cut_solution(price, 10))
![]()
最长公共子序列
问题分析
一个序列的子序列是在该序列中删去若干元素后得到的序列。比如ABCD与BDF都是ABCDEFG的子序列。
给定两个序列X与Y,求X与Y的最长公共子序列:
例如:X = ABBCBDE Y = DBBCDB 最长公共子序列 = BBCD

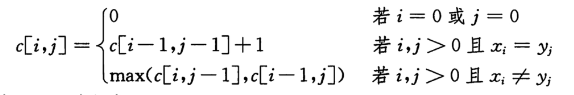
X与Y最后一个字母不同,则去掉X/Y最后一个字母对于最长公共子序列的结果不影响。

代码实现:最大长度
def MaxLength_CommonChildArray(x, y): m = len(x) n = len(y) c = [[0 for _ in range(n + 1)] for _ in range(m + 1)] for i in range(1, m + 1): for j in range(1, n + 1): # 下表是从1开始的,判断最后一个字母是否相同 if x[i - 1] == y[j - 1]: # c[i][j] = c[i - 1][j - 1] + 1 # 从左上方过来的值 else: c[i][j] = max(c[i - 1][j], c[i][j - 1]) return c[m][n] i = 'ABCBDAB' j = 'BDCABA' print(MaxLength_CommonChildArray(i, j))
代码重构:输出序列
def MaxLength_CommonChildArray_Print(x, y): # 输出 m = len(x) n = len(y) c = [[0 for _ in range(n + 1)] for _ in range(m + 1)] # 记录当前的箭头: 1-斜箭头 2-上箭头 3-左箭头 arrow = [[0 for _ in range(n + 1)] for _ in range(m + 1)] for i in range(1, m + 1): for j in range(1, n + 1): # 下表是从1开始的,判断最后一个字母是否相同 if x[i - 1] == y[j - 1]: c[i][j] = c[i - 1][j - 1] + 1 # 从左上方过来的值 arrow[i][j] = 1 elif c[i - 1][j] > c[i][j - 1]: c[i][j] = c[i - 1][j] arrow[i][j] = 2 else: c[i][j] = c[i][j - 1] arrow[i][j] = 3 return c[m][n], arrow def lcs_print(x, y): c, b = MaxLength_CommonChildArray_Print(x, y) i = len(x) j = len(y) res = [] while i > 0 and j > 0: if b[i][j] == 1: res.append(x[i - 1]) i -= 1 j -= 1 elif b[i][j] == 2: # 来自上方 i -= 1 else: # 来自左方 j -= 1 return "".join(reversed(res))

本文来自博客园,作者:{张一默},转载请注明原文链接:https://www.cnblogs.com/YiMo9929/p/17822854.html





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
2022-12-14 C++:类模板知识回顾