DS博客作业03--树
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| :----: | :----: | :----: |
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 | 陈宇杭 |
0. PTA得分截图

1. 本周学习总结
1.1 二叉树结构
1.1.1 二叉树的2种存储结构
- 二叉树有顺序存储结构和链式存储结构两种存储结构。
-
顺序存储结构
二叉树的顺序存储结构就是用一组地址连续的存储单元来存放二叉树的数据元素,因此必须确定好树种各数据元素的存放次序,使得各数据元素在这个存放次序中的相互位置能反映出数据元素之间的逻辑关系。
对于一般二叉树,则需要添加一些并不存在的空结点,令其成为一颗完全二叉树形式。
顺序存储结构结构体定义
typedef ElemType SqBinTree[MaxSize]; -
链式存储结构
二叉树的链式存储结构是指用一个链表来存储一棵二叉树,二叉树中的每一个节点用链表中的一个节点来储存。
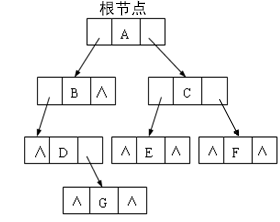
链式存储结构结构体定义
typedef struct BNode { char data;//存放数据 BNode* Lchild;//节点左孩子 BNode* Rchild;//节点右孩子 }; -
两种存储方式的优与劣
顺序存储结构
优点:节点的数据是按照层次依次按顺序排列,并可以通过下标的关系确定双亲与孩子的关系,结构简约而复杂;
缺点:在存储非满二叉树时,需要添加额外节点来凑成完全二叉树,会对空间造成极大的浪费,同时使得二叉树的插入删除等操作不够便捷;链式存储结构
优点:对于顺序结构更加直观的体现二叉树之间节点的关系,同时在存储非满二叉树时比较节省存储空间,并且支持多种遍历方式;
缺点:相邻节点的关系虽然紧密,但寻找某个特定的节点则需要遍历二叉树,并不算方便;
-
1.1.2 二叉树的构造
-
通过顺序表构造二叉树
已知一个二叉树的完整顺序序列,可通过顺序表中的节点关系来构造二叉树;
在顺序序列中,若头结点用1表示,则双亲与孩子的关系为(双亲 i,左孩子 2i,右孩子 2i+1);
如此按顺序构建二叉树;代码
BeTree PreCreateTree(int& i, string str)
{
if (i < length)
{
if (str[i] == '#')
return NULL;
BeTree T = new BNode;
T->data = str[i];
T->Lchild = PreCreateTree(++i, str);
T->Rchild = PreCreateTree(++i, str);
return T;
}
else
return NULL;
}
-
通过给定遍历序列构造二叉树
已知一个二叉树的给定遍历序列,如abc##de#g##f###,其中NULL节点用'#'表示;
便可直接根据对应方式直接构造二叉树;- 先序
BTree PreCreateBT(string str,int&i) { if(i>=len-1) return NULL; if(str[i]=='#') return NULL; BTree bt=new BTnode; bt->data=str[i]; bt->lchild=PreCreateBT(str,++i); bt->rchild=PreCreateBT(str,++i); }- 中序
BTree InoCreateBT(string str,int&i) { if(i>=len-1) return NULL; if(str[i]=='#') return NULL; BTree bt=new BTnode; bt->lchild=InoCreateBT(str,++i); bt->data=str[i]; bt->rchild=InoCreateBT(str,++i); }- 后序
BTree PostCreateBT(string str,int&i) { if(i>=len-1) return NULL; if(str[i]=='#') return NULL; BTree bt=new BTnode; bt->lchild=PostCreateBT(str,++i); bt->rchild=PostCreateBT(str,++i); bt->data=str[i]; } -
给定先序遍历序列和中序遍历序列构造二叉树
已知先序遍历序列,便可得到根节点的节点数据,再根据中序遍历序列得到根节点左右两边的节点序列;
以此进行递归,便可得到完整的二叉树;代码
BeTree RestoreBeTree(char* preFront, char* preRear, char* inoFront, char* inoRear)//直接传入对应字符串的位置来进行遍历
{
int i = 0;
BeTree T = new BNode;
T->data = *(preFront + i);
while (*(inoFront + i) != *preFront) i++; //得到根节点在中序遍历序列中的位置
if (*(inoFront + i) == *inoRear && *(inoFront + i) == *inoFront)//判断左右子树是否存在
{
T->Lchild = NULL;
T->Rchild = NULL;
}
else if (*(inoFront + i) == *inoRear)
{
T->Lchild = RestoreBeTree(preFront + 1, preFront + i, inoFront, inoFront + i - 1);
T->Rchild = NULL;
}
else if (*(inoFront + i) == *inoFront)
{
T->Lchild = NULL;
T->Rchild = RestoreBeTree(preFront + i + 1, preRear, inoFront + i + 1, inoRear);
}
else
{
T->Lchild = RestoreBeTree(preFront + 1, preFront + i, inoFront, inoFront + i - 1);
T->Rchild = RestoreBeTree(preFront + i + 1, preRear, inoFront + i + 1, inoRear);
}
return T;
}
-
给定后序遍历序列和中序遍历序列构造二叉树
原理同上,因为是后序遍历所以略有不同;
代码
BeTree RestoreBeTree(int* postFront, int* postRear, int* inoFront, int* inoRear)
{
int i = 0;
BeTree T = new BNode;
T->data = *postRear;
while (*(inoFront + i) != *postRear) i++; //得到根节点在中序遍历序列中的位置
if (*(inoFront + i) == *inoRear && *(inoFront + i) == *inoFront)//判断左右子树是否存在
{
T->Lchild = NULL;
T->Rchild = NULL;
}
else if (*(inoFront + i) == *inoRear)
{
T->Lchild = RestoreBeTree(postFront, postFront + i - 1, inoFront, inoFront + i - 1);
T->Rchild = NULL;
}
else if (*(inoFront + i) == *inoFront)
{
T->Lchild = NULL;
T->Rchild = RestoreBeTree(postFront + i, postRear - 1, inoFront + i + 1, inoRear);
}
else
{
T->Lchild = RestoreBeTree(postFront, postFront + i - 1, inoFront, inoFront + i - 1);
T->Rchild = RestoreBeTree(postFront + i, postRear - 1, inoFront + i + 1, inoRear);
}
return T;
}
1.1.3 二叉树的遍历
-
二叉树的遍历共四种,分别为先序遍历,中序遍历,后序遍历以及层次遍历;
- 先序遍历
void PreorderPrintLeaves(BinTree BT) { if (BT != NULL) { cout<<BT->Data<<" "; PreorderPrintLeaves(BT->Left); PreorderPrintLeaves(BT->Right); } }- 中序遍历
void PreorderPrintLeaves(BinTree BT) { if (BT != NULL) { PreorderPrintLeaves(BT->Left); cout<<BT->Data<<" "; PreorderPrintLeaves(BT->Right); } }- 后序遍历
void PreorderPrintLeaves(BinTree BT) { if (BT != NULL) { PreorderPrintLeaves(BT->Left); PreorderPrintLeaves(BT->Right); cout<<BT->Data<<" "; } }- 层序遍历
void LevelorderTraversal(BinTree BT) { if (BT == NULL) return; queue<BinTree>Que; BinTree front; Que.push(BT); while (!Que.empty()) { front = Que.front(); Que.pop(); printf("%c", front->data); if (front->lchild != NULL) Que.push(front->lchild); if (front->rchild != NULL) Que.push(front->rchild); } }
1.1.4 线索二叉树
- 线索二叉树设计
线索二叉树,是通过创建线索的方式来利用上原本二叉树的NULL节点,使其指向对应遍历序列的前驱或后继,让查找更加方便;
根据遍历序列的不同,线索二叉树又分为先序线索二叉树、中序线索二叉树和后序线索二叉树;
因此在原有二叉树节点结构体上,额外增加两个标志来判断指针为线索还是孩子;
左标志ltag=0 表示lchild指向左孩子节点; 左标志ltag=1 表示lchild指向前驱节点;
右标志ltag=0 表示lchild指向右孩子节点; 右标志ltag=1 表示lchild指向后继节点

-
结构体修改如下
typedef struct node { ElemType data; //结点数据域 int ltag, rtag; //增加的线索标记 struct node * lchild; //左孩子或线索指针 struct node * rchild; //右孩子或线索指针 } BTNode; //线索二叉树中的结点类型
-
中序线索二叉树特点
- 结点的后继为其右子树中最左下的结点;
- 节点的前驱为其左子树时最后一个访问的结点;
-
代码层面
void Inothread(BiTree root)//创建线索二叉树
{ if(root!=NULL)
{
Inothread(root->lchild);
if(root->lchild == NULL)
{
root->lchild = pre;
root->ltag = 1;
}
if(pre != NULL && pre->rchild == NULL)
{
pre->rchild = root;
pre->Rtag = 1;
}
pre = root;
Inothread(root->lchild);
}
}
BiTree InoPre(BiTree p)//找前驱
{
if(p->ltag == 1)
pre = p->lchild;
else{
for(q=p->lchild;q->rtag==0;q=q->rchild)
pre = q;
}
return pre;
}
BiTree InoNext(BiTree p)//找后继
{
if(p->rtag == 1)
next = p->rchild;
else{
for(q=p->rchild;q->ltag==0;q=q->lchild)
next = q;
}
return next;
}
1.1.5 二叉树的应用--表达式树
在表达式中,各个运算符都具有自己的优先级,如先括号,再乘除,后加减;
而中序遍历比较特殊,在中序遍历下恰好可以满足算式的计算优先级;通常二叉树的层次越深,优先级越高;左右子树表示运算顺序;
- 表达式树如何构造
用栈结构来存储运算符和运算数值等数据;
通过出栈入栈等操作来创建二叉树,并将根节点(存储主要运算符)入栈存储;
如果遇到优先级更高的运算符,则重复创建二叉树并入栈根节点操作;
如果遇到优先级更低的运算符
{
则将根节点数据依次出栈并进行优先级比较,直到出栈的运算符优先级小于此遇到的运算符;
将此前出栈的所有树按顺序连接,先出栈的为后出栈的右孩子节点;
以遇到的运算符创建根节点,并将合并后的树的根节点作为新树的左孩子,并将其入栈;
}
重复操作,直到遍历完数据;
返回二叉树的根节点;
代码
展开
void InitExpTree(BTree& T, string str) //建表达式的二叉树
{
char exp1 = '#', exp2 = '#';
int i = 0;
int len = str.size();
stack Sb;
BTree root = new BiTNode;
root->data = '#';
root->lchild = NULL;
root->rchild = NULL;
Sb.push(root);
for (i = 0; i < len + 1; i++)
{
if (str[i] >= '0' && str[i] <= '9')
{
BTree BT = new BiTNode;
exp1 = Sb.top()->data;
BT->data = str[i];
BT->lchild = NULL;
BT->rchild = NULL;
Sb.push(BT);
continue;
}
else if (In(str[i]))
{
exp2 = str[i];
BTree BT = new BiTNode;
BT->lchild = NULL;
BT->rchild = NULL;
BT->data = str[i];
if (exp2 == '(')
Sb.push(BT);
else if (exp2 == ')')
{
BTree B2 = Sb.top();
Sb.pop();
BTree B1 = Sb.top();
Sb.pop();
Sb.pop();
B1->rchild = B2;
exp1 = Sb.top()->data;
Sb.push(B1);
}
else if (Precede(exp1, exp2) == '<')
{
BTree B = Sb.top();
Sb.pop();
BT->lchild = B;
Sb.push(BT);
}
else if (Precede(exp1, exp2) == '>')
{
char exp = 0;
do
{
BTree B1 = Sb.top();
Sb.pop();
BTree B2 = Sb.top();
Sb.pop();
exp = Sb.top()->data;
B2->rchild = B1;
Sb.push(B2);
} while (Precede(exp,exp2) != '<');
BTree B = Sb.top();
BT->lchild = B;
Sb.pop();
Sb.push(BT);
}
}
else if (str[i] == 0)
{
do
{
BTree B1 = Sb.top();
Sb.pop();
BTree B2 = Sb.top();
if (B2->data == '#')
{
T = B1;
break;
}
Sb.pop();
B2->rchild = B1;
Sb.push(B2);
} while (1);
}
}
}
- 如何计算表达式树
中序遍历表达式二叉树,采用递归返回值进行运算;
代码
展开
double EvaluateExTree(BTree T)//计算表达式树
{
if (T->lchild == NULL && T->rchild == NULL)
return T->data - '0';
else
{
if (T->data == '+')
return EvaluateExTree(T->lchild) + EvaluateExTree(T->rchild);
if (T->data == '-')
return EvaluateExTree(T->lchild) - EvaluateExTree(T->rchild);
if (T->data == '*')
return EvaluateExTree(T->lchild) * EvaluateExTree(T->rchild);
if (T->data == '/')
{
if (EvaluateExTree(T->rchild) == 0)
{
cout << "divide 0 error!" << endl;
exit(0);
}
else
return EvaluateExTree(T->lchild) / EvaluateExTree(T->rchild);
}
}
}
1.2 多叉树结构
1.2.1 多叉树结构
多叉树是树的一个基本类型,通常为一个双亲对应多个孩子;
多叉树的存储结构分为:双亲存储结构,孩子链存储结构,孩子兄弟链存储结构
- 双亲存储结构
以顺序表存储节点数据,额外开辟一个储存空间来记录每个节点的双亲节点在顺序表上的位置;
结构体定义如下;
typedef struct
{
ElemType data;
int parent;
} PTree[MaxSize];
- 孩子链存储结构
以链表存储节点数据,每一个节点都记录着指向所有孩子的指针,在不同的树中结构体的孩子指针个数也会不同,根据其中度的最大值来设定;
结构体定义如下;
typedef struct
{
ElemType data;
struct node *sons[MaxSize];
} TSonNode;
- 孩子兄弟链存储结构
以链表结构进行存储数据,每个节点记录着第一个孩子的指针位置,以及和自己同双亲的另一个兄弟指针;

结构体定义如下;
typedef struct tnode{
ElemType data; //结点的值
struct tnode* son; //指向兄弟
struct tnode* brother; //指向孩子结点
}TSBNode;
1.2.2 多叉树遍历
多叉树遍历方式总体上和二叉树思路相同,根据每棵树的最大度的不同,代码也需要相应调整;
-
若以双亲存储结构存储多叉树,则可以快速的进行层次遍历;
-
若以孩子链存储结构存储多叉树;则其先序遍历思路为:
- 先序遍历:
1) 访问根节点
2) 按照从左往右的顺序先序遍历根节点的每一棵子树
- 先序遍历:
-
若以孩子兄弟链结构存储多叉树,那它本质上就是一颗二叉树,去上面找代码;
1.3 哈夫曼树
1.3.1 哈夫曼树定义
-
定义
哈夫曼树:又称最优二叉树,给定N个权值作为N个叶子结点,构造一棵二叉树,该树的带权路径长度是最小的二叉树。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。 -
用途
哈夫曼树可用于构造使电文编码的代码长度最短的编码方案,以及解决与带权路径长度有关的问题;
1.3.2 哈夫曼树的结构体
哈夫曼树也同二叉树,有顺序存储结构和链式存储结构两种方式存储数据;
typedef struct node //顺序结构
{
char data;//节点值
float weight;//权重
int parent;//双亲节点
int lchild;//左孩子节点
int rchild;//右孩子节点
}HTNode;
typedef struct node;//链式结构
{
char data; //结点数据
float weight; //权重
struct node* parent; //双亲节点
struct node* lchild; //左孩子
struct node* rchild; //右孩子
struct node* next; //指向下一个节点
}HTNode;
1.3.3 哈夫曼树构建及哈夫曼编码
- 主要思路及步骤
步骤一.根据给定的n个权值{w1,w2,……wn},构造n棵只有根结点的二叉树;BT={T1,T2,…,Tn}。
步骤二.在BT中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树,这棵新的二叉树根结点的权值为其左、右子树根结点权值之和。
步骤三.在集合BT中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合BT中。
步骤四.重复步骤一、二,当BT中只剩下一棵二叉树时,这棵二叉树便是所要建立的哈夫曼树。
给定一串权值数据{1,2,2,5,9},并将所有数据构造成节点放入BT中;
选出其中最小的节点'1'和次小的节点'2'构造成新的二叉树,将根节点赋上两个节点权值的和'3';
删除最小和次小的节点,并将新节点并入BT;并排序;
重复上述操作,直到构建出一颗完整的树并返回根节点;
- 哈夫曼编码
哈夫曼编码是可变字长编码的一种,是哈夫曼于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码;
哈夫曼树的应用很广,哈夫曼编码就是其在电讯通信中的应用之一。
广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。
在电讯通信业务中,通常用二进制编码来表示字母或其他字符,并用这样的编码来表示字符序列。
如果需传送的电文为 ‘ABACCDA’,它只用到四种字符,则可以以电文中的字符作为叶子结点构造二叉树。
然后将二叉树中结点引向其左孩子的分支标 ‘0’,引向其右孩子的分支标 ‘1’;
每个字符的编码即为从根到每个叶子的路径上得到的 0, 1 序列。如此得到的即为二进制前缀编码。
以字母出现的次数作为权值构造哈夫曼树;
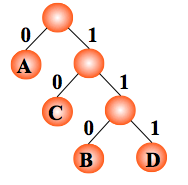
编码: A:0, C:10,B:110,D:111
- 哈夫曼树代码
结构体
typedef struct BNode
{
int weight;
int parent;
int Lchild;
int Rchild;
};
创建哈夫曼树函数
void CreateHFMTree(BeTree node,int& len)
{
int min = -1, nextmin = -1;
int i;
for (i = 0; i < len; i++)
{
if (node[i].parent == -1)
{
if (min == -1)
min = i;
else if (node[i].weight < node[min].weight)
{
nextmin = min;
min = i;
}
else if (node[i].weight >= node[min].weight)
{
if (nextmin == -1)
nextmin = i;
else if (node[i].weight < node[nextmin].weight)
nextmin = i;
}
}
}
node[min].parent = len;
node[nextmin].parent = len;
node[len].parent = -1;
node[len].Lchild = min;
node[len].Rchild = nextmin;
node[len].weight = node[min].weight + node[nextmin].weight;
len++;
return;
}
1.4 并查集
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
- 定义
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示。
- 用途及优势
用途:求无向图的连通分量个数、最小公共祖先、带限制的作业排序,实现Kruskar算法求最小生成树等。
优势:能够实现较快的合并和判断元素所在集合
- 结构体、查找、合并操作
结构体
typedef struct BNode {
int data;
int rank;
int parent;
}BNode, * BeTree;
查找
int FindRoot(BeTree BT, int n)
{
int m = n;
while (BT[m].data != BT[m].parent) m = BT[m].parent;
return m;
}
合并
int trueRoot = FindRoot(BT, root);
for (j = 0; j < p - 1; j++)
{
cin >> num;
int numRoot = FindRoot(BT, num);
if (trueRoot != numRoot)
{
BT[trueRoot].rank += BT[numRoot].rank;
BT[numRoot].parent = trueRoot;
}
}
1.5 谈谈你对树的认识及学习体会
俗话说得好,人不能在一颗树上吊死,但我可以XD;
树作为一种存储结构,完美地体现了分而治之的原则;
在操作树的过程中少不了递归的使用,在不断的递归中,将大事化小,小事化大;
2. PTA实验作业
2.1 二叉树叶子结点带权路径长度和
代码展开
#include
#include
#include
using namespace std;
int length;
typedef struct BNode
{
char data;
BNode* Lchild;
BNode* Rchild;
};
typedef BNode* BeTree;
BeTree CreateTree(int i, string str);//顺序表创建二叉树
void PreOrderLevel(BeTree T, int h, int& len);
int main()
{
int i = 1;
string str;
cin >> str;
length = str.size();
BeTree T = NULL;
T = CreateTree(i,str);
int len = 0;
PreOrderLevel(T,0,len);
cout << len <data = str[i];
Node->Lchild = CreateTree(2 * i, str);
Node->Rchild = CreateTree(2 * i + 1, str);
return Node;
}
else
return NULL;
}
void PreOrderLevel(BeTree T,int h,int &len)
{
if (!T || T->data == '#')
return;
else
{
if (T->Rchild == NULL && T->Lchild == NULL)
len += (T->data - '0') * h;
PreOrderLevel(T->Lchild, h + 1,len);
PreOrderLevel(T->Rchild, h + 1,len);
}
}
2.1.1 解题思路及伪代码
- 主要思路
首先根据题中所给顺序表数据构建二叉树;
遍历二叉树,找到所有叶节点并记录其高度与权值的积;
将所有叶节点的最终数据相加得到带权路径长度和;
- 伪代码
读入数据;
根据所给数据构建二叉树;
遍历二叉树
{
如果是叶节点
带权路径长度和 += 该叶节点高度 * 权值;
}
输出带权路径长度和;
2.1.2 总结解题所用的知识点
顺序表法构建二叉树;
寻找记录某节点的高度;
二叉树的遍历;
2.2 目录树
代码展开
#include
#include
#include
#include
#include
#include
using namespace std;
#define MAX 270
typedef struct BNode
{
char fileName[MAX];
BNode* folderChild;
BNode* fileChild;
BNode* brother;
int file_flag;
};
typedef BNode* BeTree;
void CreateFileTree(BeTree T, char* str);
void PrintFileName(BeTree T, int level);
int main()
{
int n;
int i;
BeTree root = new BNode;
strcpy(root->fileName, "root\0");
root->folderChild = NULL;
root->fileChild = NULL;
root->brother = NULL;
char* str = (char*)malloc(sizeof(char) * MAX);
cin >> n;
getchar();
for (i = 0; i < n; i++)
{
cin >> str;
CreateFileTree(root, str);
}
PrintFileName(root, 0);
return 0;
}
void PrintFileName(BeTree T, int level)
{
if (!T)
return;
for (int i = 0; i < level; i++) cout << " ";
cout << T->fileName << endl;
PrintFileName(T->folderChild, level + 1);
PrintFileName(T->fileChild, level + 1);
PrintFileName(T->brother, level);
}
void CreateFileTree(BeTree T, char* str)
{
int fileFlag = 0;
if (*str == '\0')
{
T->folderChild = NULL;
return;
}
char* p = strchr(str, '\\');
if (!p && *str != '\0')
{
p = strchr(str, '\0');
fileFlag = 1;
}
int len = p - str;
BeTree BT = new BNode;
BT->folderChild = NULL;
BT->fileChild = NULL;
BT->brother = NULL;
strncpy(BT->fileName, str, len);
BT->fileName[len] = 0;
if(fileFlag)
{
BeTree fileChild = T->fileChild;
BeTree pre = T;
while (fileChild)
{
if (strcmp(fileChild->fileName, BT->fileName) > 0)
{
if (pre == T)
T->fileChild = BT;
else
pre->brother = BT;
BT->brother = fileChild;
return;
}
else if (strcmp(fileChild->fileName, BT->fileName) == 0)
return;
pre = fileChild;
fileChild = fileChild->brother;
}
if (pre == T)
T->fileChild = BT;
else
pre->brother = BT;
return;
}
else
{
BeTree folderChild = T->folderChild;
BeTree pre = T;
while (folderChild)
{
if (strcmp(folderChild->fileName, BT->fileName) > 0)
{
if (pre == T)
T->folderChild = BT;
else
pre->brother = BT;
BT->brother = folderChild;
CreateFileTree(BT, p + 1);
return;
}
else if (strcmp(folderChild->fileName, BT->fileName) == 0)
{
CreateFileTree(folderChild, p + 1);
return;
}
pre = folderChild;
folderChild = folderChild->brother;
}
if (pre == T)
T->folderChild = BT;
else
pre->brother = BT;
CreateFileTree(BT, p + 1);
return;
}
}
2.2.1 解题思路及伪代码
- 主要思路
以孩子兄弟链存储文件相关数据;根据题意设两个孩子链,文件孩子链和文件夹孩子链,分别存储文件和文件夹数据;
按照所给数据遍历,若无此文件或文件夹,则新建节点接入对应指针;
- 伪代码
读入数量数据n;
创建根节点root;
循环n次{
读入字符串;
处理字符串(分离);
寻找每一串字符是否对应文件夹
如果对应
进入此文件夹,继续遍历;
如果不对应
根据文件类型按字典顺序接入文件链或文件夹链或对应兄弟链;
}
先序遍历,依次按格式输出;
2.2.2 总结解题所用的知识点
字符串处理;
孩子兄弟链的应用;
字典序排序;
先序遍历操作;
3. 阅读代码
3.1 题目及解题代码

代码展开
int num;
void flatten(struct TreeNode* root) {
num = 0;
struct TreeNode** l = (struct TreeNode**)malloc(0);
preorderTraversal(root, &l);
for (int i = 1; i < num; i++) {
struct TreeNode *prev = l[i - 1], *curr = l[i];
prev->left = NULL;
prev->right = curr;
}
free(l);
}
void preorderTraversal(struct TreeNode* root, struct TreeNode*** l) {
if (root != NULL) {
num++;
(*l) = (struct TreeNode**)realloc((*l), sizeof(struct TreeNode*) * num);
(*l)[num - 1] = root;
preorderTraversal(root->left, l);
preorderTraversal(root->right, l);
}
}
3.2 该题的设计思路及伪代码
将二叉树展开为单链表,主要考察先序遍历和建树操作和部分细节;
- 伪代码
读取顺序表;
构建二叉树;
先序遍历二叉树并记录先序序列;
按照先序遍历序列构建单链表;
遍历单链表并输出答案
3.3 分析该题目解题优势及难点
将二叉树展开为单链表之后,单链表中的节点顺序即为二叉树的前序遍历访问各节点的顺序;
因此,可以对二叉树进行前序遍历,获得各节点被访问到的顺序;
将二叉树展开为链表之后会破坏二叉树的结构,因此在前序遍历结束之后更新每个节点的左右子节点的信息;
最后将二叉树展开为单链表;
- 难点
二叉树的遍历转换;
二叉树的建树操作;



