RSA加密算法

 

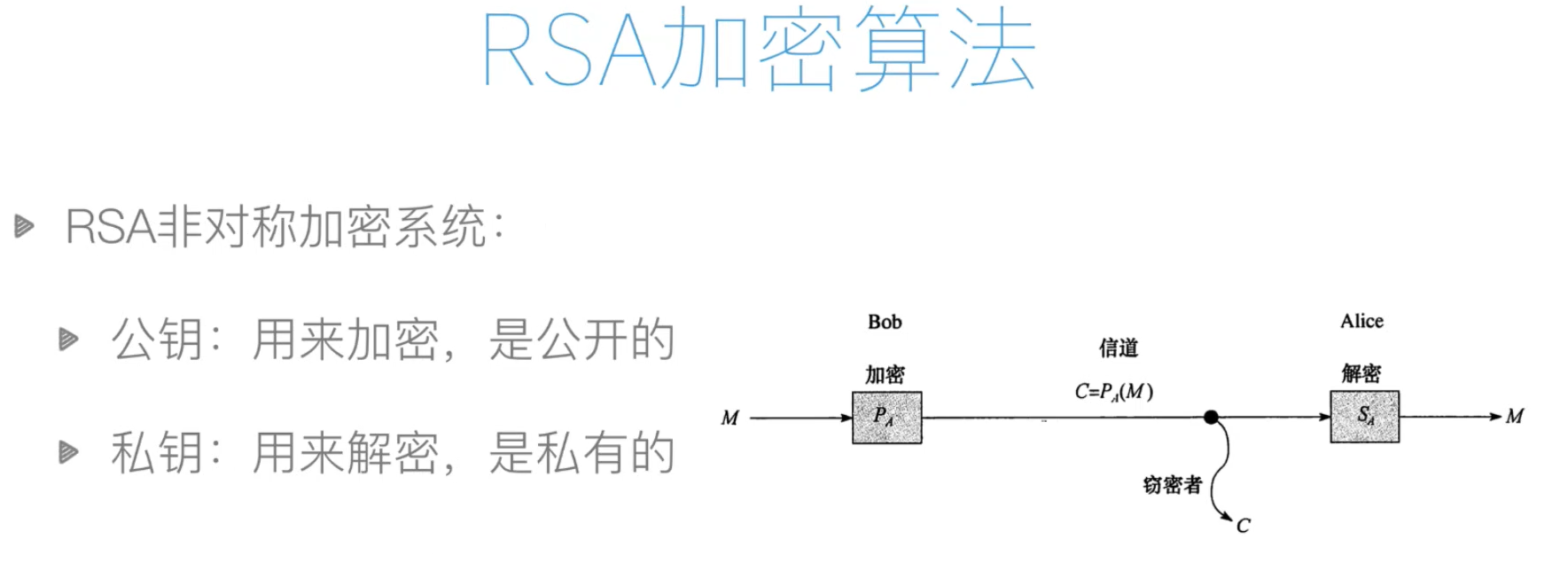
RSA算法运用了数学“两个大的质数相乘，难以在短时间内将其因式分解”的这么一套看似简单事实上真的是很困难的一个数学难题......

RSA加密算法的安全性

当p和q是一个大素数的时候，从它们的积pq去分解因子p和q，这是一个公认的数学难题。然而，虽然RSA的安全性依赖于大数的因子分解，但并没有从理论上证明破译RSA的难度与大数分解难度等价。 1994年彼得·秀尔（Peter Shor）证明一台量子计算机可以在多项式时间内进行因数分解。假如量子计算机有朝一日可以成为一种可行的技术的话，那么秀尔的算法可以淘汰RSA和相关的衍生算法。（即依赖于分解大整数困难性的加密算法） 另外，假如N的长度小于或等于256位，那么用一台个人电脑在几个小时内就可以分解它的因子了。1999年，数百台电脑合作分解了一个512位长的N。1997年后开发的系统，用户应使用1024位密钥，证书认证机构应用2048位或以上。  

RSA加密算法的缺点

虽然RSA加密算法作为目前最优秀的公钥方案之一，在发表三十多年的时间里，经历了各种攻击的考验，逐渐为人们接受。但是，也不是说RSA没有任何缺点。由于没有从理论上证明破译RSA的难度与大数分解难度的等价性。所以，RSA的重大缺陷是无法从理论上把握它的保密性能如何。在实践上，RSA也有一些缺点： 产生密钥很麻烦，受到素数产生技术的限制，因而难以做到一次一密； 分组长度太大，为保证安全性，n 至少也要 600 bits 以上，使运算代价很高，尤其是速度较慢