动态规划DP算法

 

 

 

、

 

 

 

 

 

 

 

 

 

 

 

 

python实现钢条切割问题与最长工公共序列问题

#动态规划算法DP代码：

#递归法计算斐波那契数列f(n)=f(n-1)+f(n-2)
#递归算法-执行效率比较低，相同的问题算了好多遍—子问题的重新计算
def fibnacci(n):
    if n==1 or n==2:
        return 1
    else:
        return fibnacci(n-1)+fibnacci(n-2)
print(fibnacci(5))

#非递归算法-执行效率高
#动态规划DP思想=最优子结构，递推式子+重复子问题存储
def fibnacci1(n):
    f=[0,1,1]
    if n>2:
        for i in range(n-2):
            num=f[-1]+f[-2]
            f.append(num)
    return f[n]
print(fibnacci1(100))

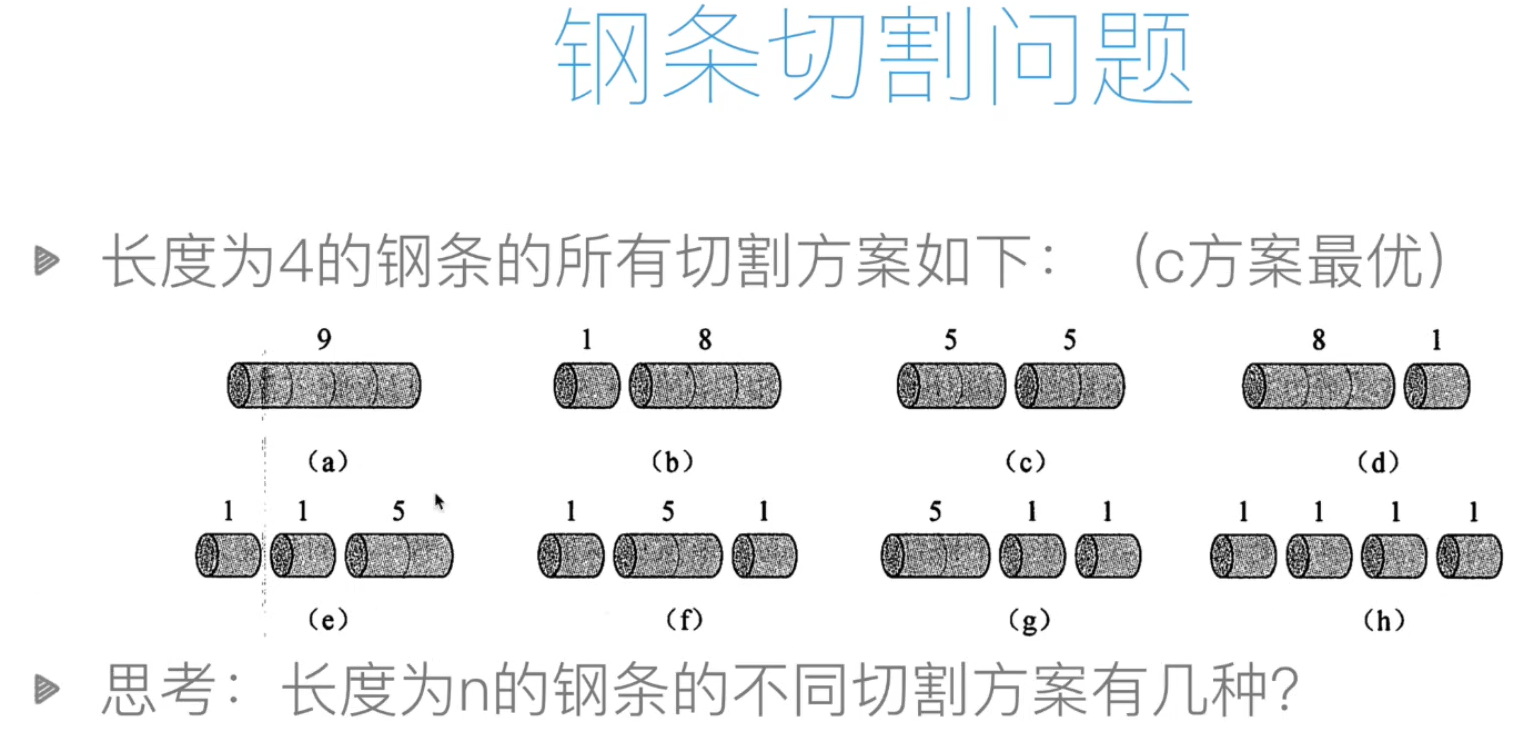
#钢条切割问题的递归算法
from cal_time import *
p=[0,1,5,8,9,10,17,17,20,21,23,24,26,27,27,28,30,33,36,39,40]
P=[0,1,5,8,9,10,17,17,20,24,30]

#使用递归的思想进行计算算法1
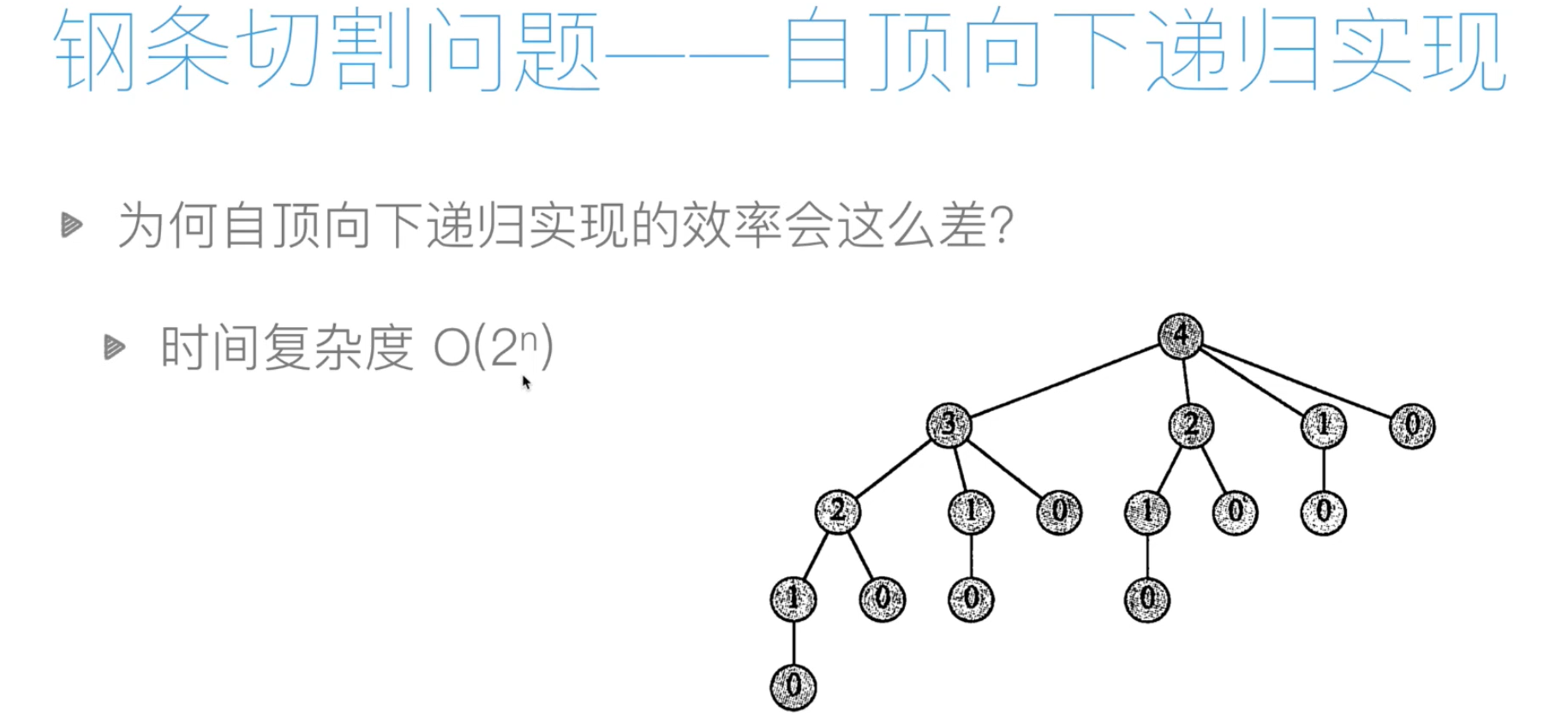
#自定向顶上，时间复杂度度为O（2**n）
def cut_rod_recurision(p,n):
    if n==0:
        return 0
    else:
        res=p[n]
        for i in range(1,n):
            res=max(res,cut_rod_recurision(p,i)+cut_rod_recurision(p,n-i))
        return res
#使用递归的思想计算算法2
def cut_rod_recurision2(p,n):
    if n==0:
        return 0
    else:
        res=0
        for i in range(1,n+1):
            res=max(res,p[i]+cut_rod_recurision2(p,n-i))
        return res

#使用动态规划DP的思想实现钢条切割问题
#自底向上思想
@cal_time
def cut_rod_DP(p,n):
    r=[0]
    for i in range(1,n+1):
        res=0
        for j in range(1,i+1):
            res=max(res,p[j]+r[i-j])
        r.append(res)
    return r[n]

#输出解决方案的切割长度函数
def cut_rod_extend(p,n):
    r=[0]  #最优的解对应的值
    s=[0]
    for i in range(1,n+1):
        res_r=0  #记录价格的最优值
        res_s=0  #记录左边不切的部分的长度
        for j in range(1,i+1):
            if p[j]+r[i-j]>res_r:
                res_r=p[j]+r[i-j]
                res_s=j
        r.append(res_r)
        s.append(res_s)
    return r[n],s
def cut_rod_solution(p,n):
    r,s=cut_rod_extend(p,n)
    ans=[]
    while n>0:
        ans.append(s[n])
        n-=s[n]
    return ans
#递归算法输出函数运行时间需要进行函数的重新定义
@cal_time
def c1(p,n):
    return cut_rod_recurision(p,n)
@cal_time
def c2(p,n):
    return cut_rod_recurision2(p,n)

print(c1(p,15))
print(c2(p,20))
print(cut_rod_solution(p,20))
print(cut_rod_DP(p,20))

#使用动态规划DP的思想实现最长公共子序列的问题

#最长公共子序列问题
#使用动态规划算法来进行解决
def lcs_length(x,y):
    m=len(x)
    n=len(y)
    c=[[0 for _ in range(n+1)] for _ in  range(m+1)]  #创建一个m行n列的二维列表
    for i in range(1,m+1):
        for j in range(1,n+1):
            if x[i-1]==y[j-1]:    #i,j的字符匹配的时候，来自于左上方的数值+1
                c[i][j]=c[i-1][j-1]+1
            else:
                c[i][j]=max(c[i-1][j],c[i][j-1])
    return c[m][n]

def lcs(x,y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]  #1为左上方，2上方，3左方
    for i in range(1,m+1):
        for j in range(1,n+1):
            if x[i-1]==y[j-1]:    #i,j的字符匹配的时候，来自于左上方的数值+1
                c[i][j]=c[i-1][j-1]+1
                b[i][j]=1  #记录来自的方向
            elif c[i-1][j]>c[i][j-1]:  #来自于上方
                c[i][j]=max(c[i-1][j],c[i][j-1])
                b[i][j]=2
            else:
                c[i][j] = max(c[i - 1][j], c[i][j - 1])
                b[i][j]=3
    return c[m][n],b
#回溯法找回输出的最优方案
def lcs_trackback(x,y):
    c,b=lcs(x,y)
    i=len(x)
    j=len(y)
    res=[]
    while i>0 and j>0:
        if b[i][j]==1: #来自左上方
            res.append(x[i-1])
            i=i-1
            j=j-1
        elif b[i][j]==2:  #来自上方
            i-=1
        else:  #来自左方
            j-=1
    return "".join(reversed(res))

c,b=lcs("ABCBDAB","BDCABA")
print(c)
print(lcs_trackback("ABCBDAB","BDCABA"))