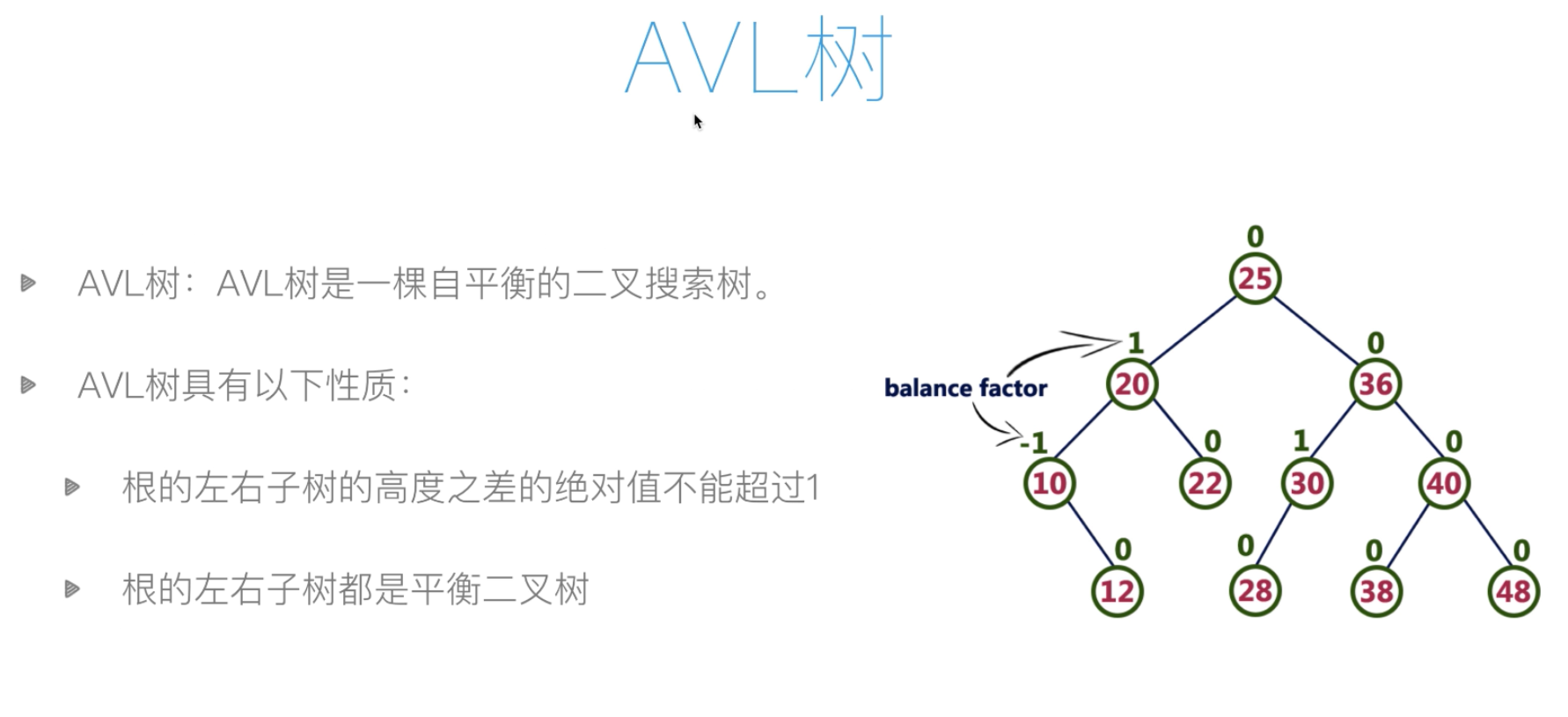
AVL树数据结构

 

 

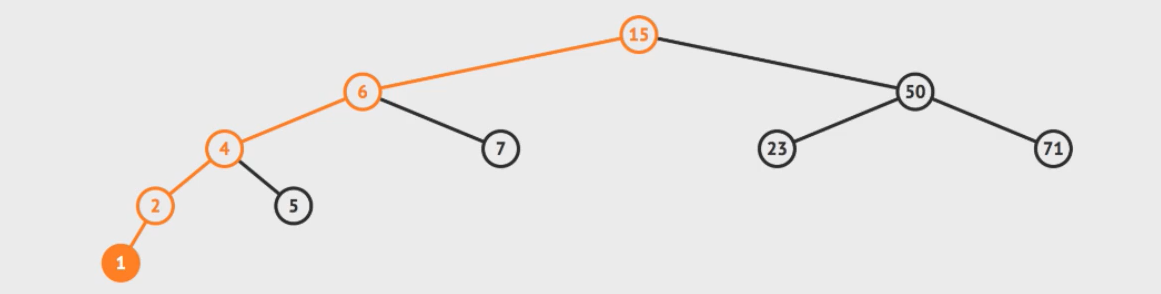
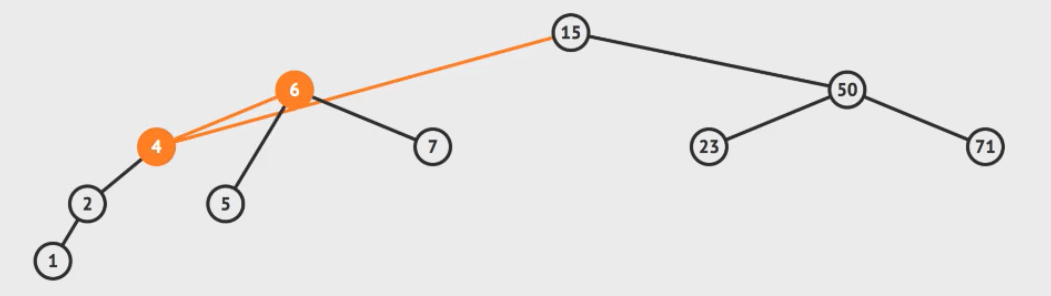
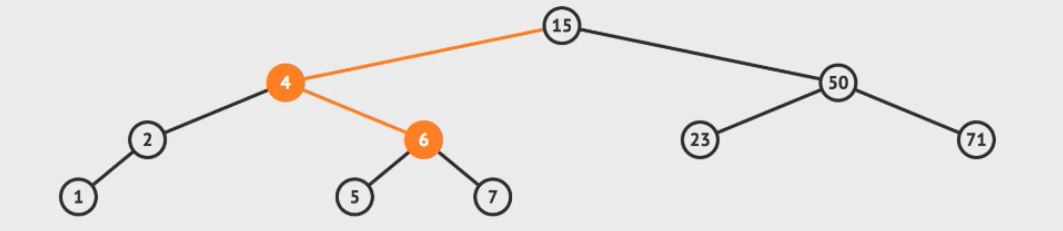
python实现AVL树的代码:

 

from BST import BiTreeNode1,BST #导入二叉搜索树的类进行继承

class AVLNode(BiTreeNode1):
    def __init__(self,data):
        BiTreeNode1.__init__(self,data)
    self.bf=0   #balance factor属性判断左右子树的高度差

class AVLTree(BST):
    def __init__(self,li=None):
        BST.__init__(self,li)

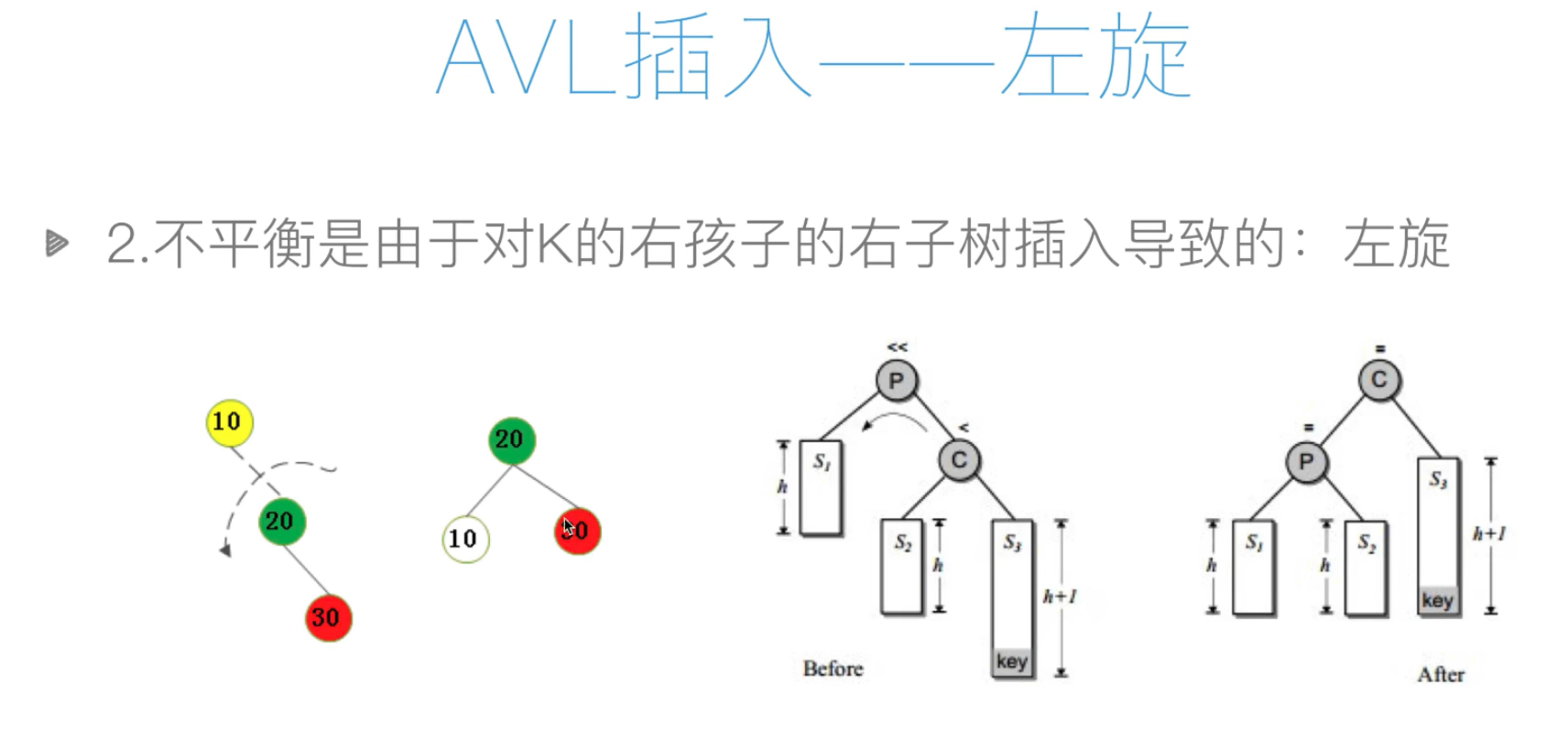
    #左旋函数-在右孩子的右子树插入元素
    def rotate_left(self,p,c):
        s2=c.lchild
        p.rchild=s2
        if s2:
            s2.parent=p
        c.lchild=p
        p.parent=c
        #插入左旋完成之后bf常数均为0
        p.bf=0
        c.bf=0
        return c
    #右旋函数-在左孩子的左子树插入元素
    def rotate_right(self,p,c):
        s2=c.rchild
        p.lchild=s2
        if s2:
            s2.parent=p
        c.rchild=p
        p.parent=c

        p.bf=0
        c.bf=0
        return c
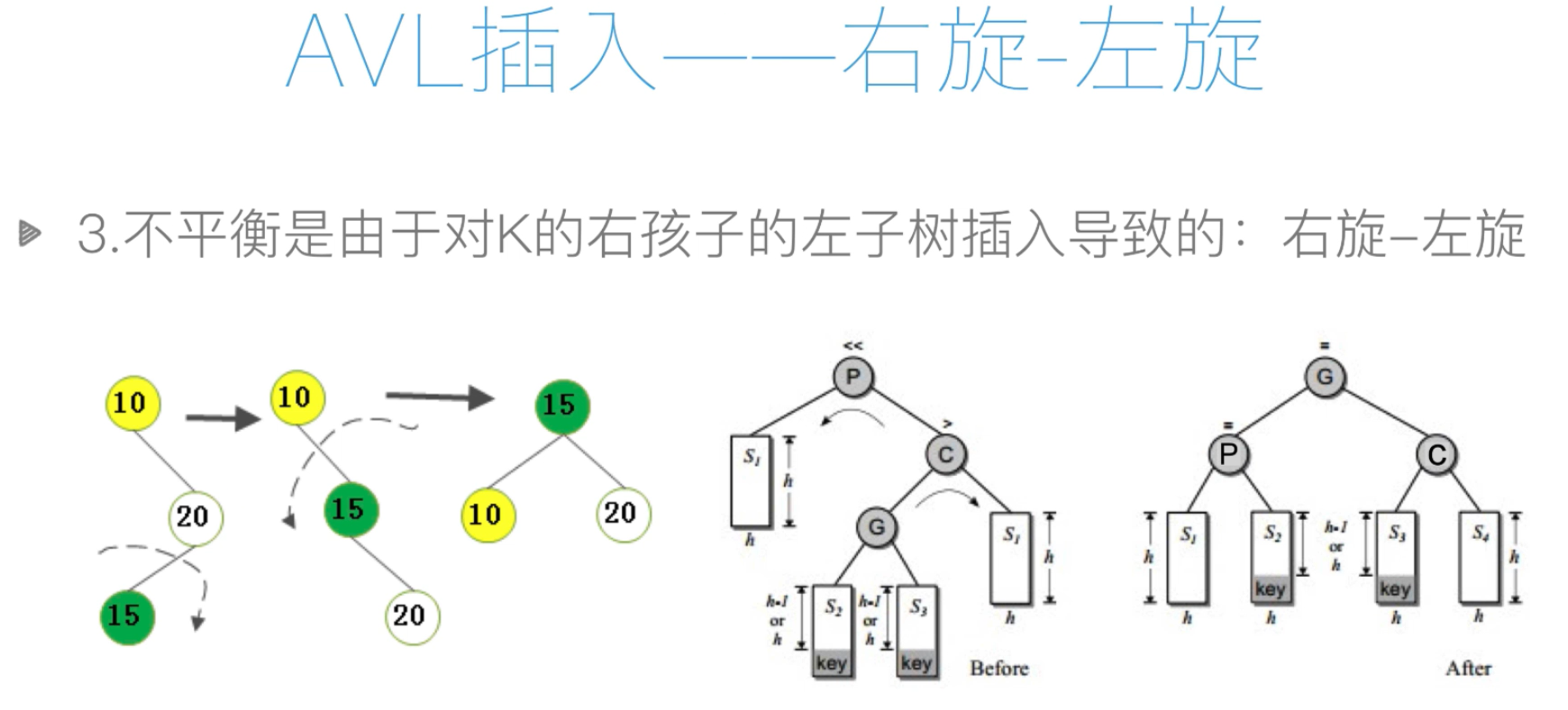
    #先右旋-后左旋函数：右孩子的左子树插入元素
    def rotate_right_left(self,p,c):
        #先右旋
        g=c.lchild
        s3=g.rchild
        c.lchild=s3
        if s3:
            s3.parent=c
        g.rchild=c
        c.parent=g
        #后左旋
        s2=g.lchild
        p.rchild=s2
        if s2:
            s2.parent=p
        g.lchild=p
        p.parent=g
        #更新bf
        if g.bf>0:
            p.bf=-1
            c.bf=0
        elif g.bf<0:
            p.bf=0
            c.bf=1
        else:
            p.bf=0
            c.bf=0
        g.bf=0
        return g
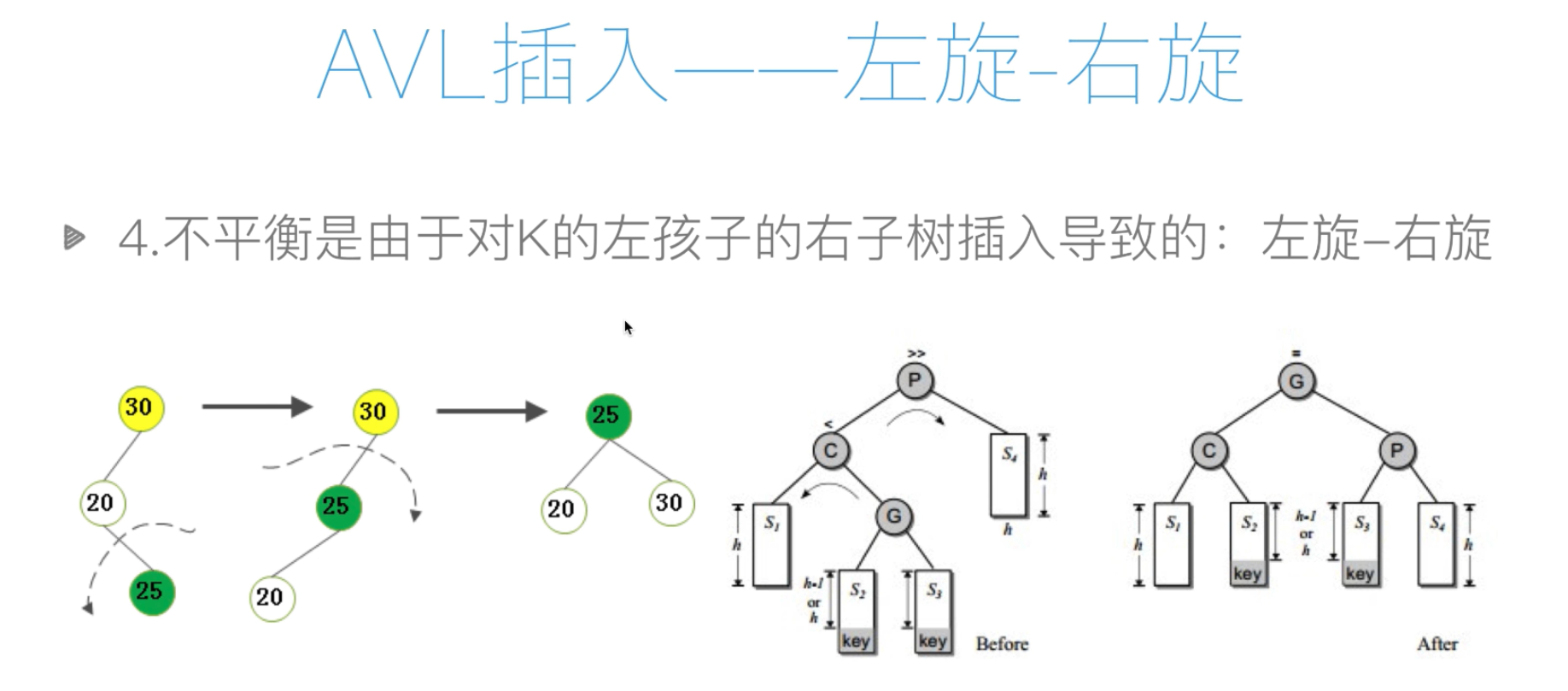
    #先左旋后右旋函数
    def rotate_left_right(self,p,c):
        g=c.rchild

        s2=g.lchild
        c.rchild=s2
        if s2:
            s2.parent=c
        g.rchild=c
        c.parent=g

        s3=g.rchild
        p.lchild=s3
        if s3:
            s3.parent=p
        g.rchild=p
        p.parent=g
        #更新bf
        if g.bf<0:
            p.bf=1
            c.bf=0
        elif g.bf>0:
            p.bf=0
            c.bf=-1
        else:
            p.bf=0
            c.bf=0
        g.bf=0
        return g
　　#插入函数
    def insert_1(self,val):
        #第一步：做插入函数
        p = self.root
        if not p:  # 空树情况下
            self.root = BiTreeNode1(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:  # 左孩子不存在
                    p.lchild = BiTreeNode1(val)
                    p.lchild.parent = p
                    node=p.lchild  #node表示插入的节点
                    break
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode1(val)
                    p.rchild.parent = p
                    node=p.rchild
                    break
            else:  #等于的节点插入
                return
        #第二步操作：更新balance factor
        while node.parent:    #node.parent不空
            if node.parent.lchild==node:  #传递是从左子树传递过来的，左子树更沉了
                #更新node.parent的bf
                if  node.parent.bf<0:  #原来的node.parent.bf=-1，更新之后变为-2，需要进行旋转调节
                    #看node哪边沉
                    g = node.parent.parent
                    x=node.parent #旋转之前子树的根
                    if node.bf>0:   #左旋右旋的情况
                        n=self.rotate_left_right(node.parent,node)
                    else:  #左旋的情况
                        n=self.rotate_right(node.parent,node)
                    #记得把n和g连接起来

                elif node.parent.bf>0:  #如果原来的大于0，为1，则更新之后变为0
                    node.parent.bf=0
                    break
                else: #原来的node.parent.bf=0，更新之后变为-1
                    node.parent.bf=-1
                    node=node.parentcontinue
            else:#传递是右子树传递来的，右子树更加沉了
                #更新node.parent+=1
                if node.parent.bf>0: #原来的node.parent.bf=1，更新之后变为2，需要进行旋转调节
                    #做旋转
                    #看node哪边沉
                    g=node.parent.parent #为了连接旋转之后的子树
                    x = node.parent  # 旋转之前子树的根
                    if node.bf<0:  #node.bf=-1，进行右旋左旋
                        n=self.rotate_right_left(node.parent,node) #n为旋转之后的子节点
                    else:
                        n=self.rotate_left(node.parent,node)
                elif node.parent.bf<0:#原来的node.parent.bf=-1，更新之后变为0
                    node.parent.bf=0
                    break
                else:#原来的node.parent.bf=0，更新之后变为1
                    node.parent.bf=1
                    node=node.parent
                    continue
            #连接旋转之后的子树，进行迭代旋转
            n.parent=g
            if g:  #如果g不是空
                if x==g.lchild:
                    g.lchild=n
                else:
                    g.rchild=n
                break
            else:
                self.root=n
                break

tree=AVLTree([9,8,7,6,5,4,3,2,1])
tree.pre_order(tree.root)
print()
tree.in_order(tree.root)