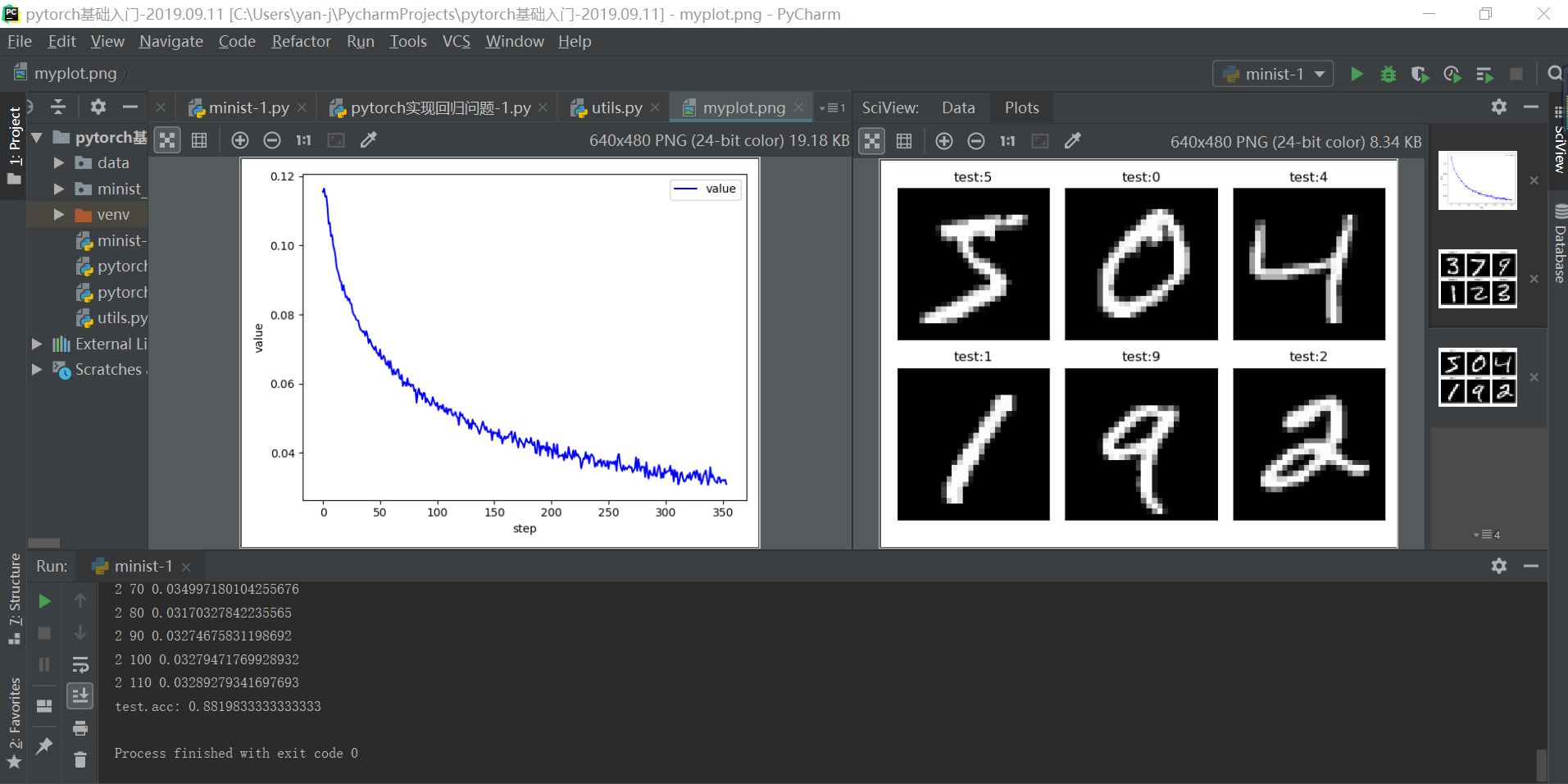
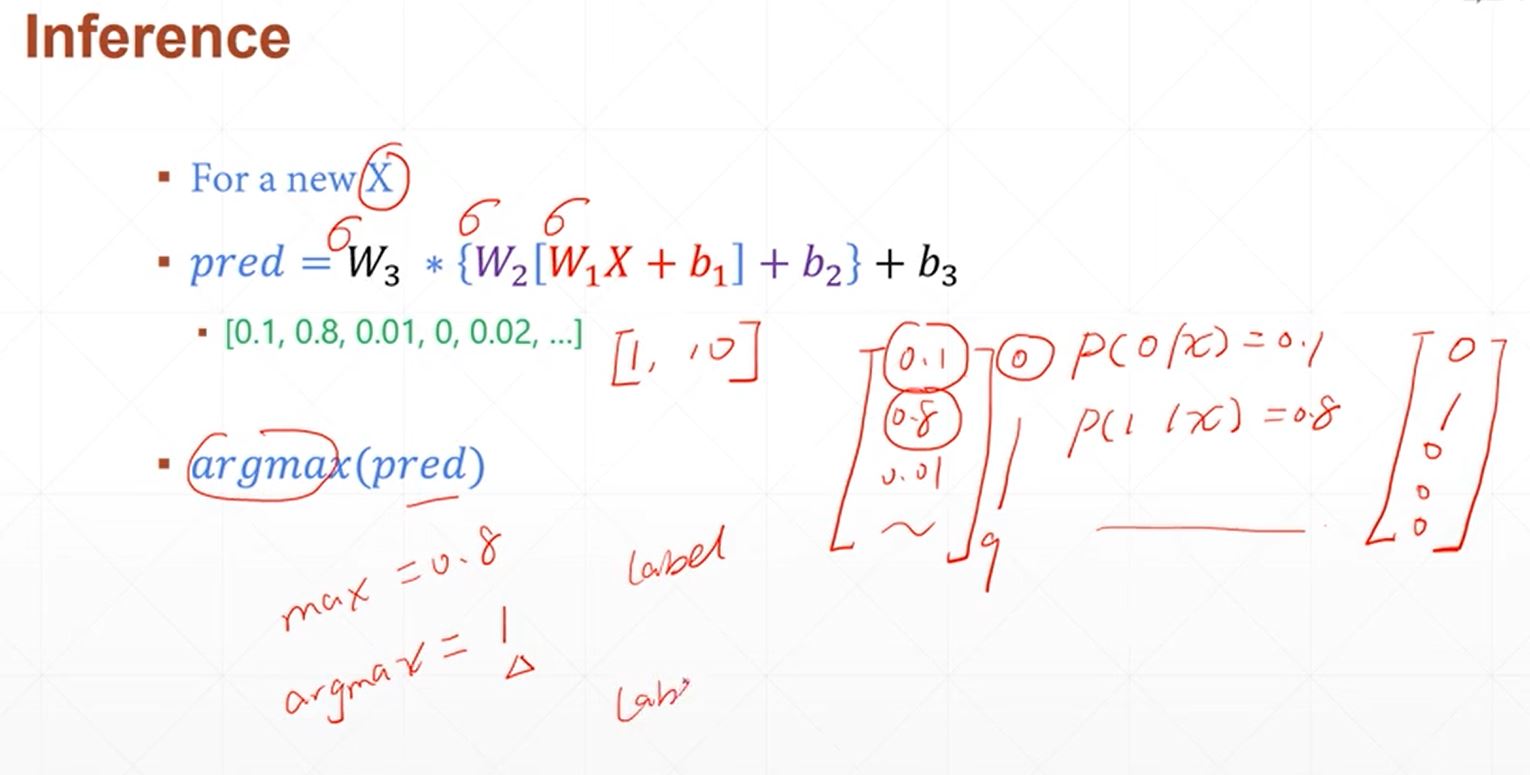利用平pytorch搭建简单的神经网络实现minist手写字体的识别,采用三层线性函数迭代运算,使得其具备一定的非线性转化与运算能力,其数学原理如下:

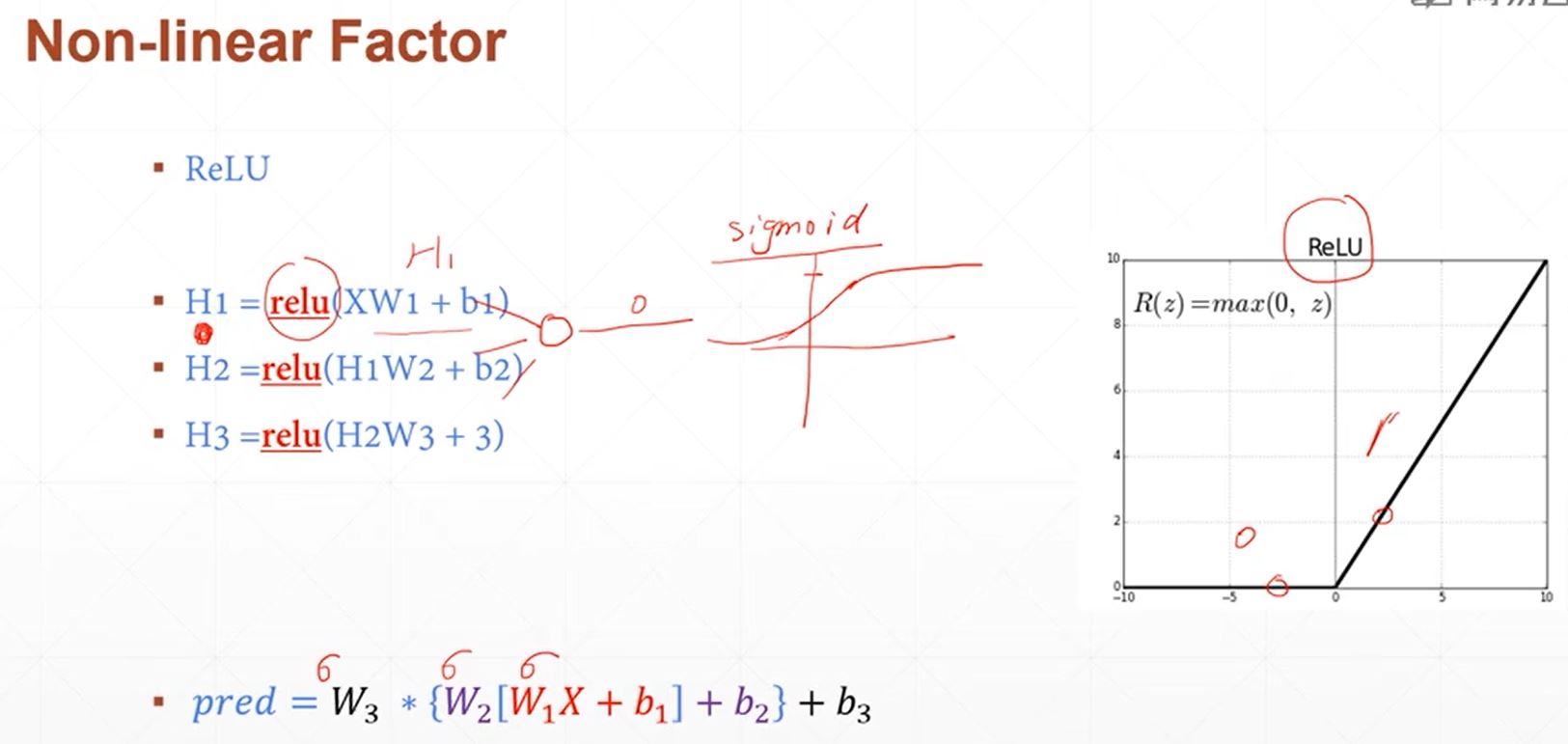
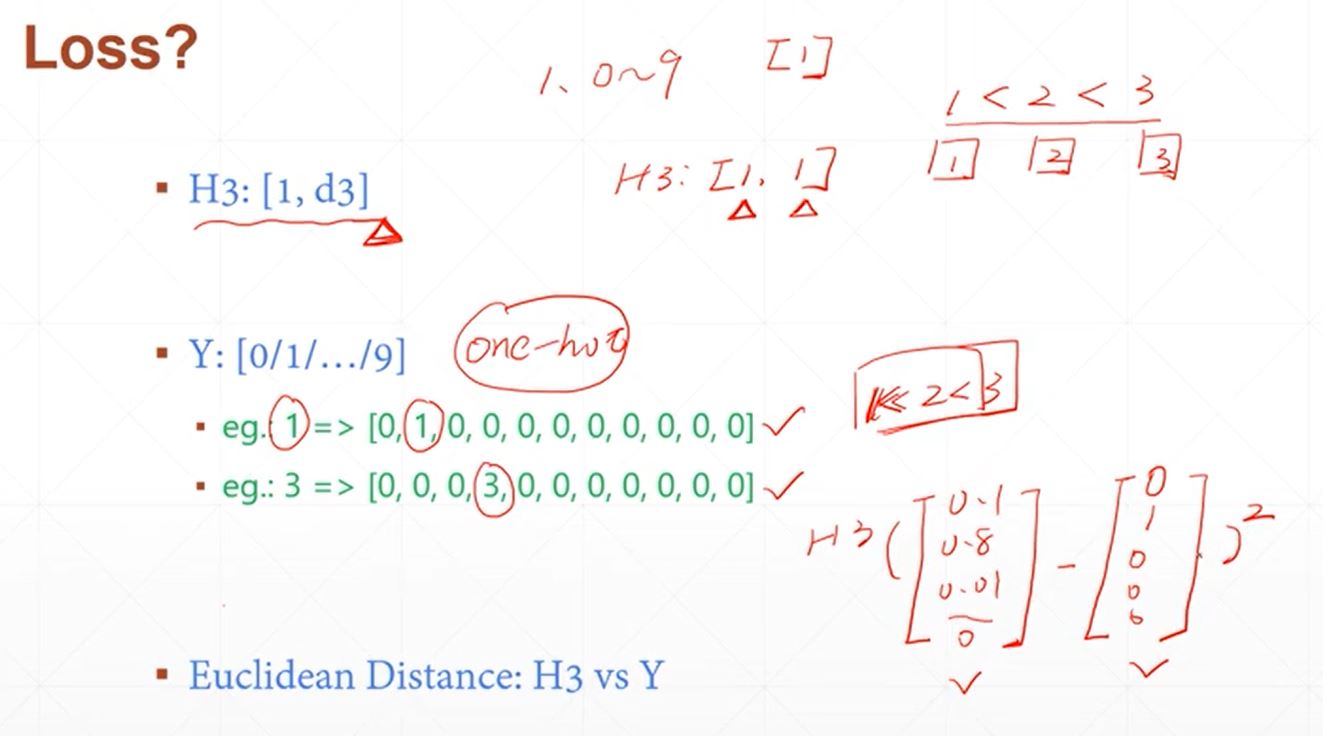
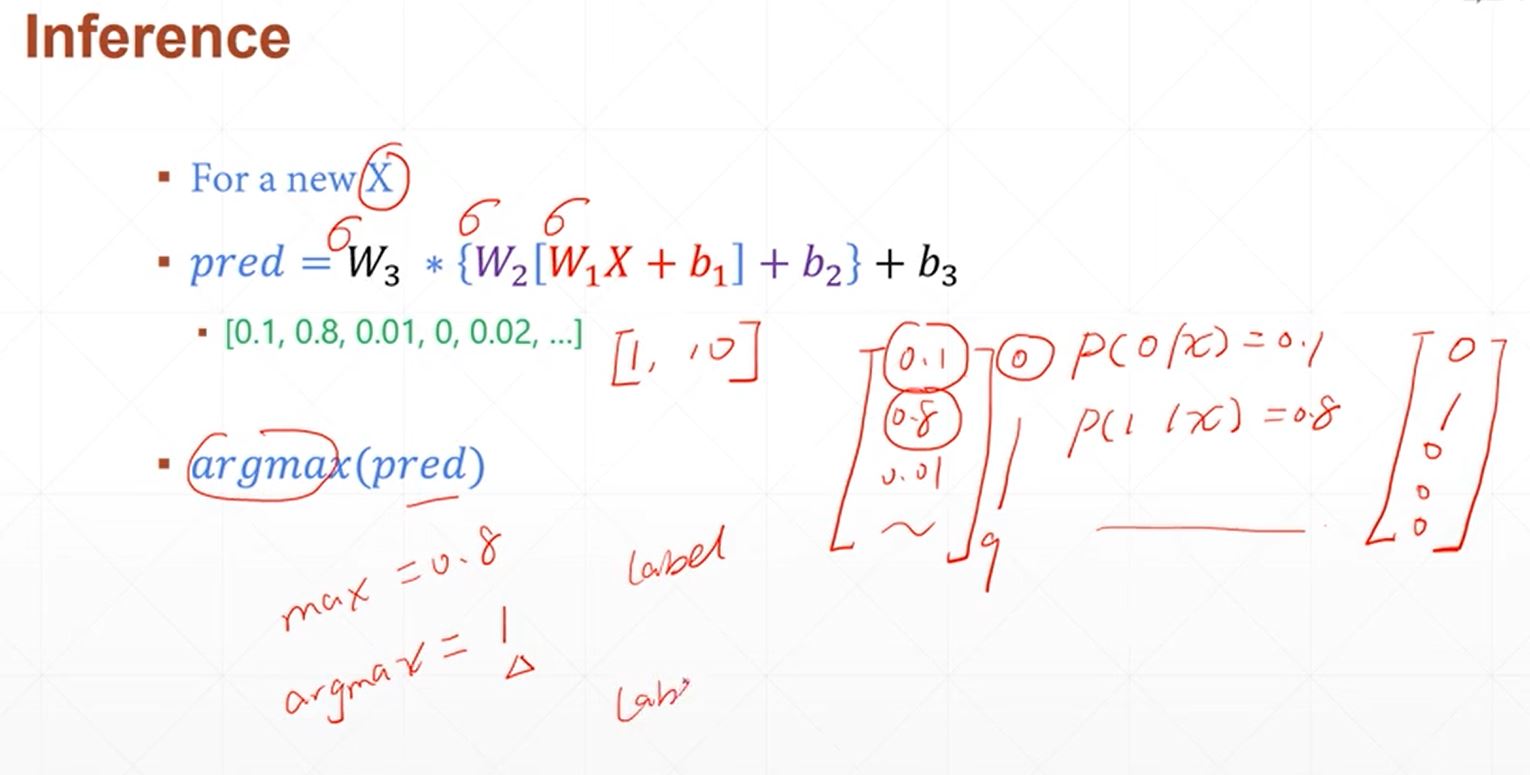
其具体实现代码如下所示:
import torch
import matplotlib.pyplot as plt
def plot_curve(data): #曲线输出函数构建
fig=plt.figure()
plt.plot(range(len(data)),data,color="blue")
plt.legend(["value"],loc="upper right")
plt.xlabel("step")
plt.ylabel("value")
plt.show()
def plot_image(img,label,name): #输出二维图像灰度图
fig=plt.figure()
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(img[i][0]*0.3081+0.1307,cmap="gray",interpolation="none")
plt.title("{}:{}".format(name, label[i].item()))
plt.xticks([])
plt.yticks([])
plt.show()
def one_hot(label,depth=10): #根据分类结果的数目将结果转换为一定的矩阵形式[n,1],n为分类结果的数目
out=torch.zeros(label.size(0),depth)
idx=torch.LongTensor(label).view(-1,1)
out.scatter_(dim=1,index=idx,value=1)
return out
batch_size=512
import torch
from torch import nn #完成神经网络的构建包
from torch.nn import functional as F #包含常用的函数包
from torch import optim #优化工具包
import torchvision #视觉工具包
import matplotlib.pyplot as plt
from utils import plot_curve,plot_image,one_hot
#step1 load dataset 加载数据包
train_loader=torch.utils.data.DataLoader(
torchvision.datasets.MNIST("minist_data",train=True,download=True,transform=torchvision.transforms.Compose(
[torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,),(0.3081,))
])),
batch_size=batch_size,shuffle=True)
test_loader=torch.utils.data.DataLoader(
torchvision.datasets.MNIST("minist_data",train=True,download=False,transform=torchvision.transforms.Compose(
[torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,),(0.3081,))
])),
batch_size=batch_size,shuffle=False)
x,y=next(iter(train_loader))
print(x.shape,y.shape)
plot_image(x,y,"image")
print(x)
print(y)
#构建神经网络结构
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
#xw+b
self.fc1=nn.Linear(28*28,256)
self.fc2=nn.Linear(256,64)
self.fc3=nn.Linear(64,10)
def forward(self, x):
#x:[b,1,28,28]
#h1=relu(xw1+b1)
x=F.relu(self.fc1(x))
#h2=relu(h1w2+b2)
x=F.relu(self.fc2(x))
#h3=h2w3+b3
x=(self.fc3(x))
return x
net=Net()
#[w1,b1,w2,b2,w3,b3]
optimizer=optim.SGD(net.parameters(),lr=0.01,momentum=0.9)
train_loss=[]
for epoch in range(3):
for batch_idx,(x,y) in enumerate(train_loader):
#x:[b,1,28,28],y:[512]
x=x.view(x.size(0),28*28)
# => [b,10]
out =net(x)
# [b,10]
y_onehot=one_hot(y)
#loss=mse(out,y_onehot)
loss= F.mse_loss(out,y_onehot)
optimizer.zero_grad()
loss.backward()
#w'=w-lr*grad
optimizer.step()
train_loss.append(loss.item())
if batch_idx %10==0:
print(epoch,batch_idx,loss.item()) #输出其预测loss损失函数的变化曲线
plot_curve(train_loss)
#get optimal [w1,b1,w2,b2,w3,b3]
total_correct=0
for x,y in test_loader:
x=x.view(x.size(0),28*28)
out=net(x)
pred=out.argmax(dim=1)
correct=pred.eq(y).sum().float().item()
total_correct+=correct
total_num=len(test_loader.dataset)
acc=total_correct/total_num
print("test.acc:",acc) #输出整体预测的准确度
x,y=next(iter(test_loader))
out=net(x.view(x.size(0),28*28))
pred=out.argmax(dim=1)
plot_image(x,pred,"test")
实现结果如下所示: