决策树算法原理

//2019.08.17
#决策树算法
1、决策树算法是一种非参数的决策算法，它根据数据的不同特征进行多层次的分类和判断，最终决策出所需要预测的结果。它既可以解决分类算法，也可以解决回归问题，具有很好的解释能力。

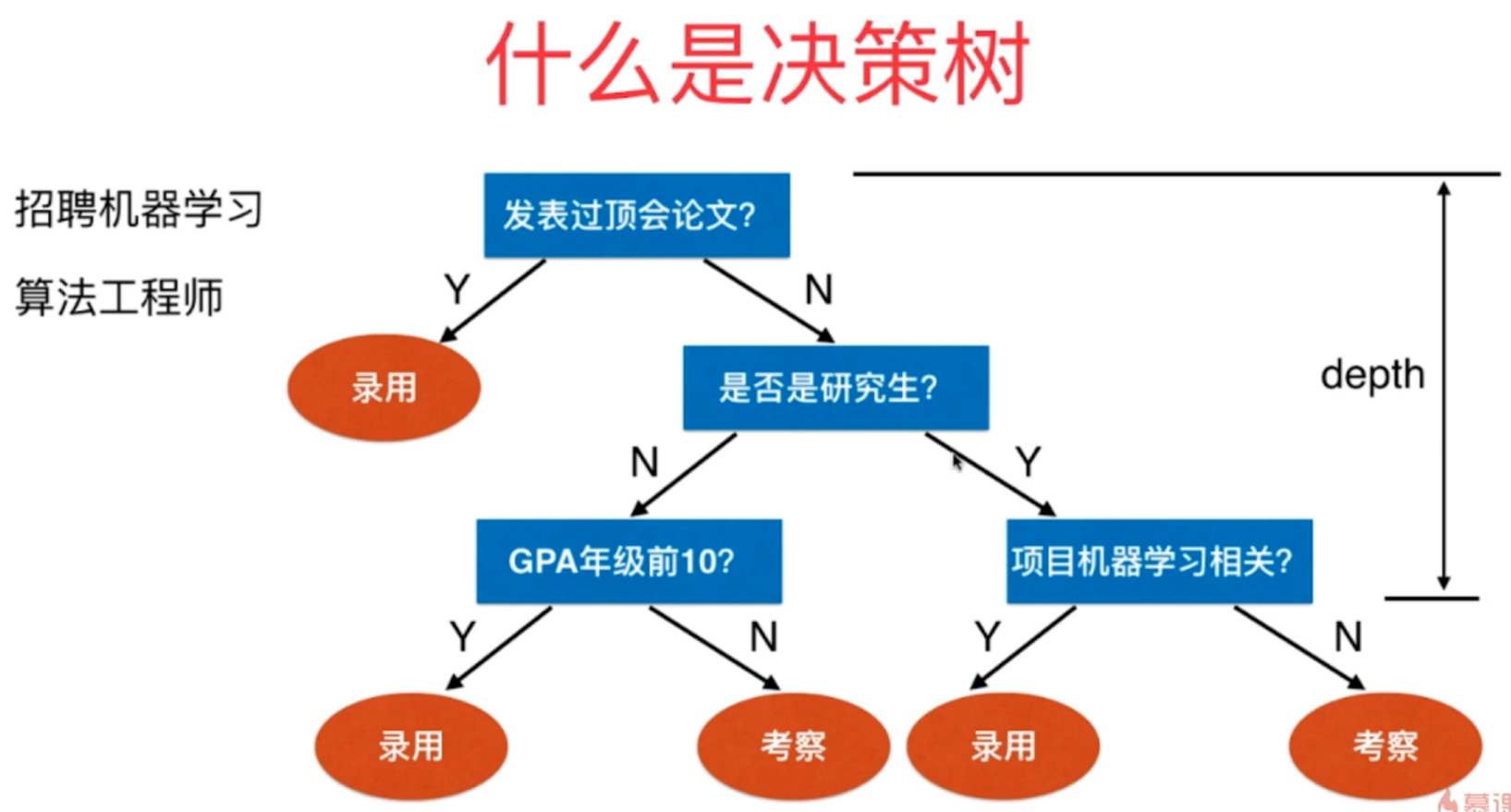
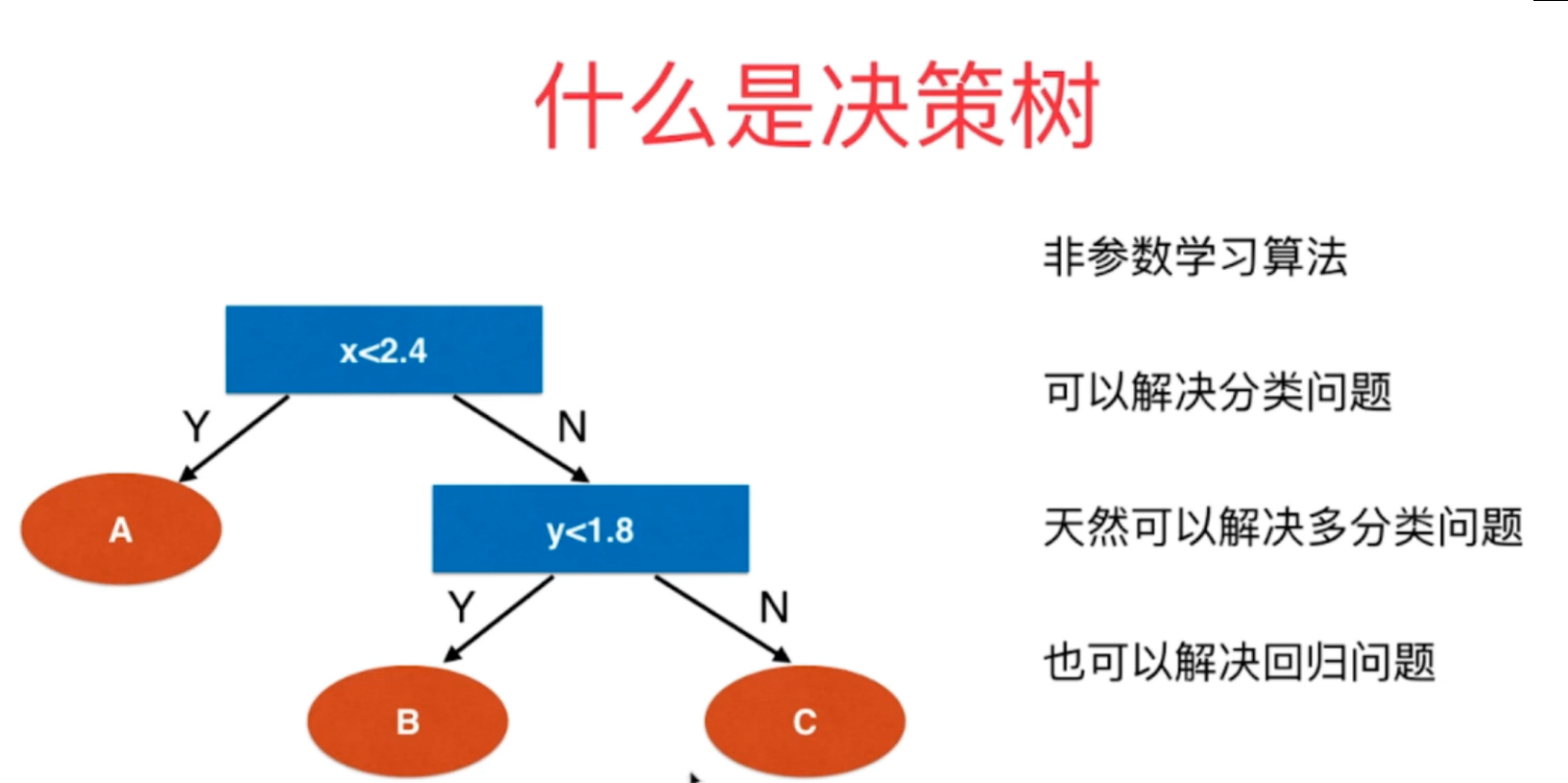
图 原理图
2、对于决策树的构建方法具有多种出发点，它具有多种构建方式，如何构建决策树的出发点主要在于决策树每一个决策点上需要在哪些维度上进行划分以及在这些维度的哪些阈值节点做划分等细节问题。

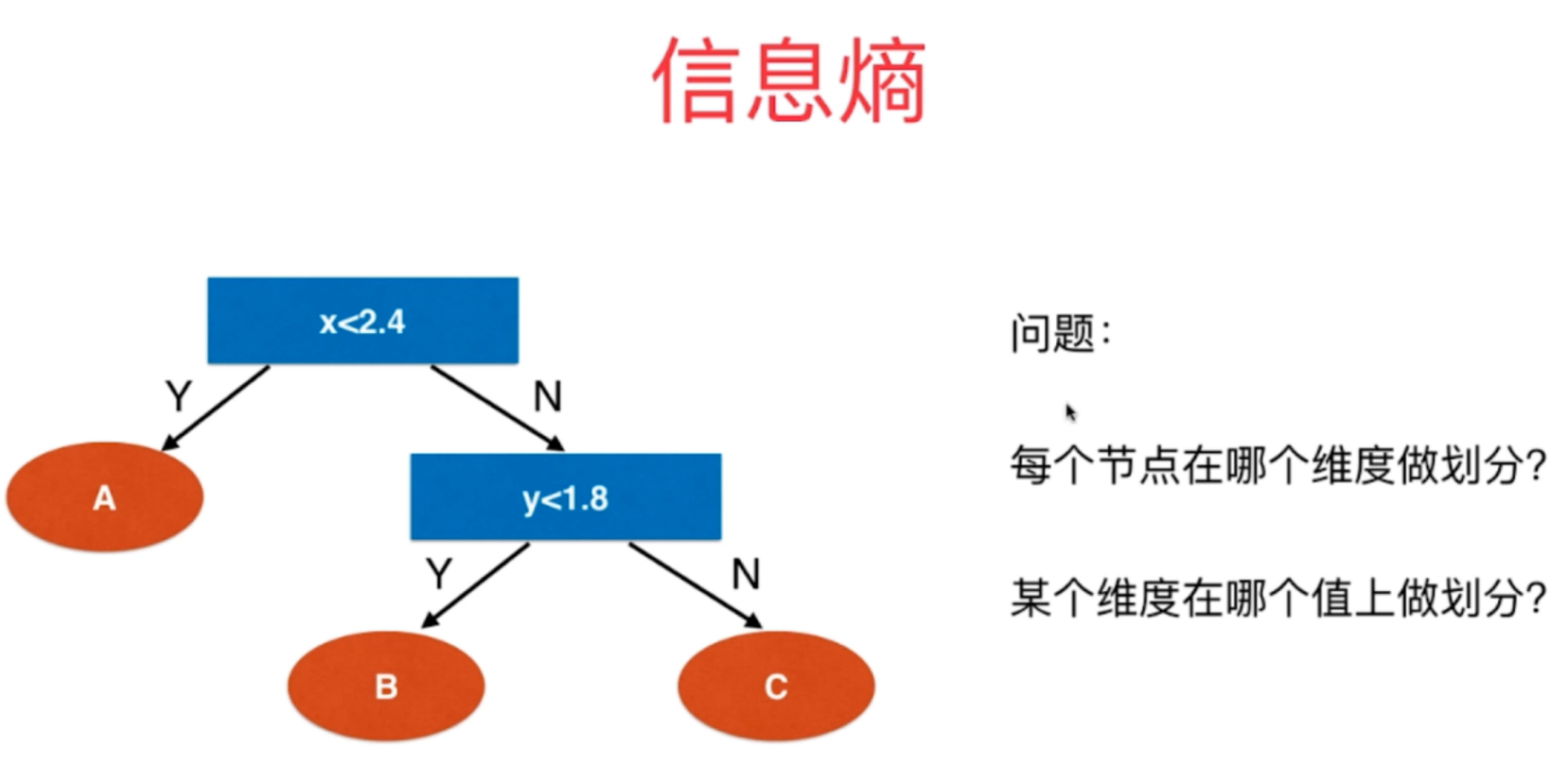
3、信息熵entropy是决策树构建过程中最为常见的一种构建方式，熵在信息论中的含义是随机变量的不确定度，熵越大，不确定性越大，越不确定，熵越小，表示不确定度越小，越确定。

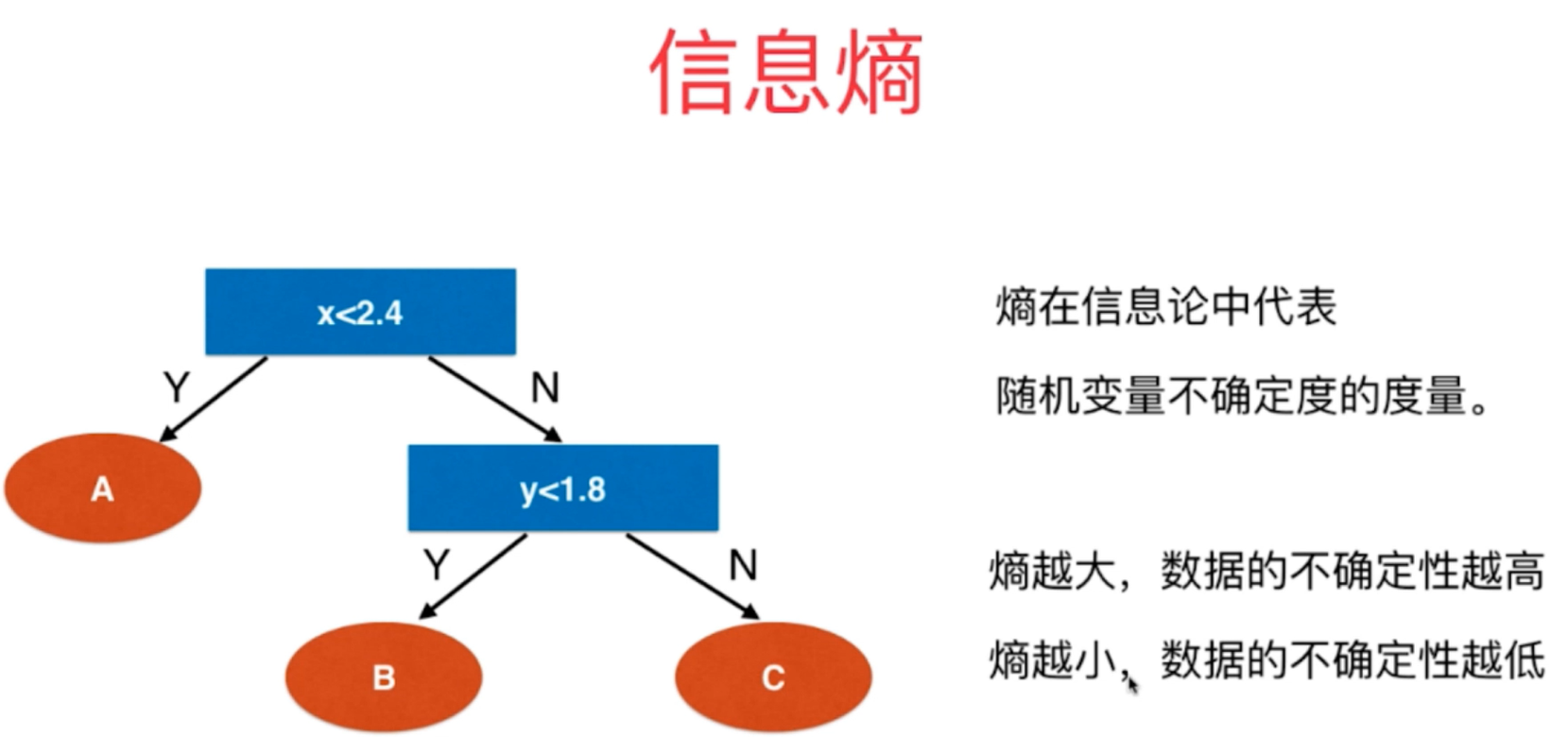
图
4、信息熵的划分方式总体原则是不断地使得整体的决策系统的熵值越来越小，使得系统越来越确定的方向发展。

5、基尼系数gini是决策树划分的另外一种方式，它和信息熵的原理是类似的，随着基尼系数的增大，整体的随机性在不断地增大。

6、对于基尼系数和信息熵的决策树划分方式，其效果一般情况下都是大致相同的，只是信息熵的计算方式比起基尼系数要慢一些，sklearn中默认选用的是基尼系数。因此，对于决策树的决策方式信息熵和基尼系数这个超参数对于模型的好坏并没有太大的影响。

7、CART的决策树形式既可以解决回归问题，也可以解决分类问题，它的思想是以数据的摸一个维度以及该维度下的阈值来进行分类和计算，它的整体数据结构是二叉树的形式。

8、决策树的训练复杂度比较高，训练过程比较复杂，时间较长，另外作为一种非参数决策算法，它很容易出现过拟合的现象。因此，我们需要对于决策树的算法进行剪枝，从而降低模型的复杂度，并且可以比较好的避免过拟合的现象。
9、决策树的主要超参数有max_depth(最大深度2-4),min_samples_split(继续拆分树时最小划分的样本总数，越小越容易过拟合，也不能太大，10左右),min_samples_leaf(最小叶子节点所必须的样本数，最小为1，越小越容易过拟合，6),max_leaf_nodes(最多拆分的节点数，越多越复杂，越容易过拟合，4)

 10、决策树的局限性：作为一种非参数的机器学习算法，它的决策边界总是平行于坐标轴的，这是由于算法的原理造成的，这个特点也造成了决策树决策边界的局限性——只能是平行于特征轴的超平面，而不能与坐标轴产生一定的的夹角(倾斜超平面)，这会使得训练数据边缘之后的数据因为决策边界划分的原因而产生很大的误差。另外，鉴于它是一种非参数学习算法，因此它对一些个别数据还是比较敏感的，这会很大程度影响模型训练的好坏。

 

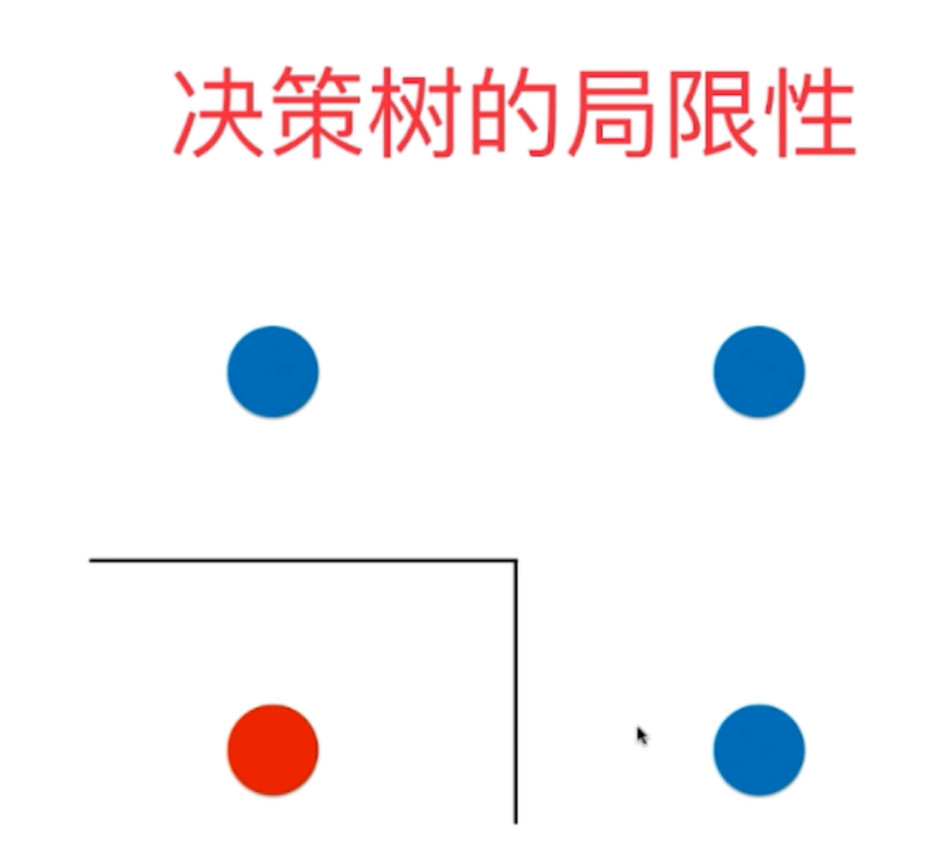
决策树的决策边界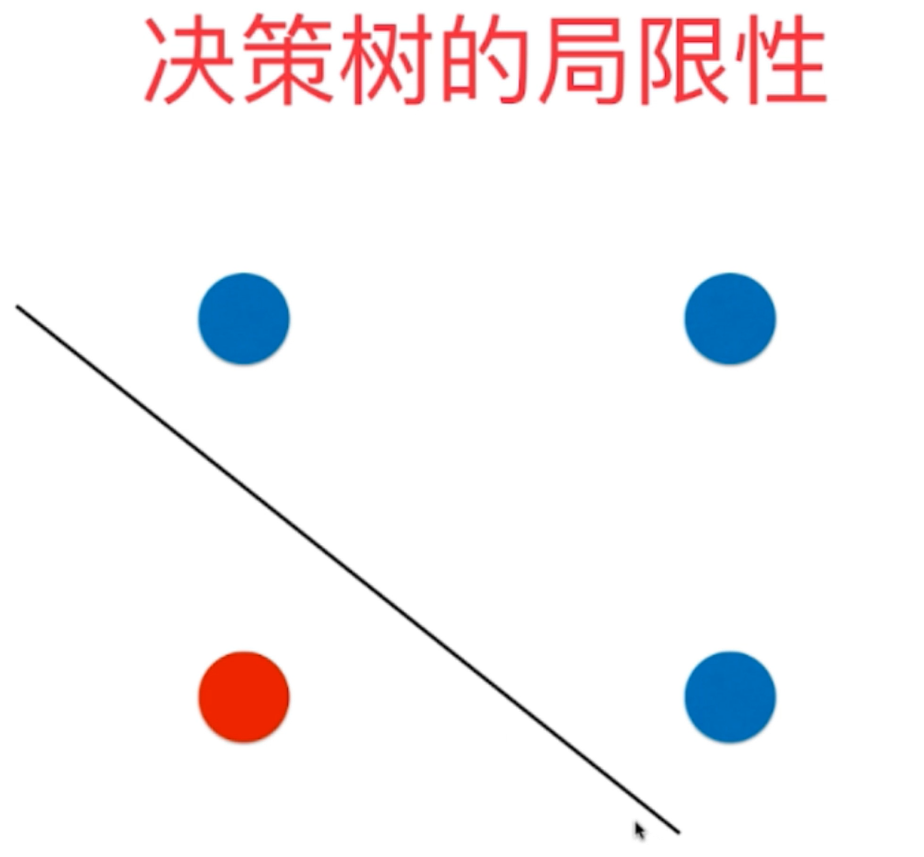

 

实际数据的划分边界

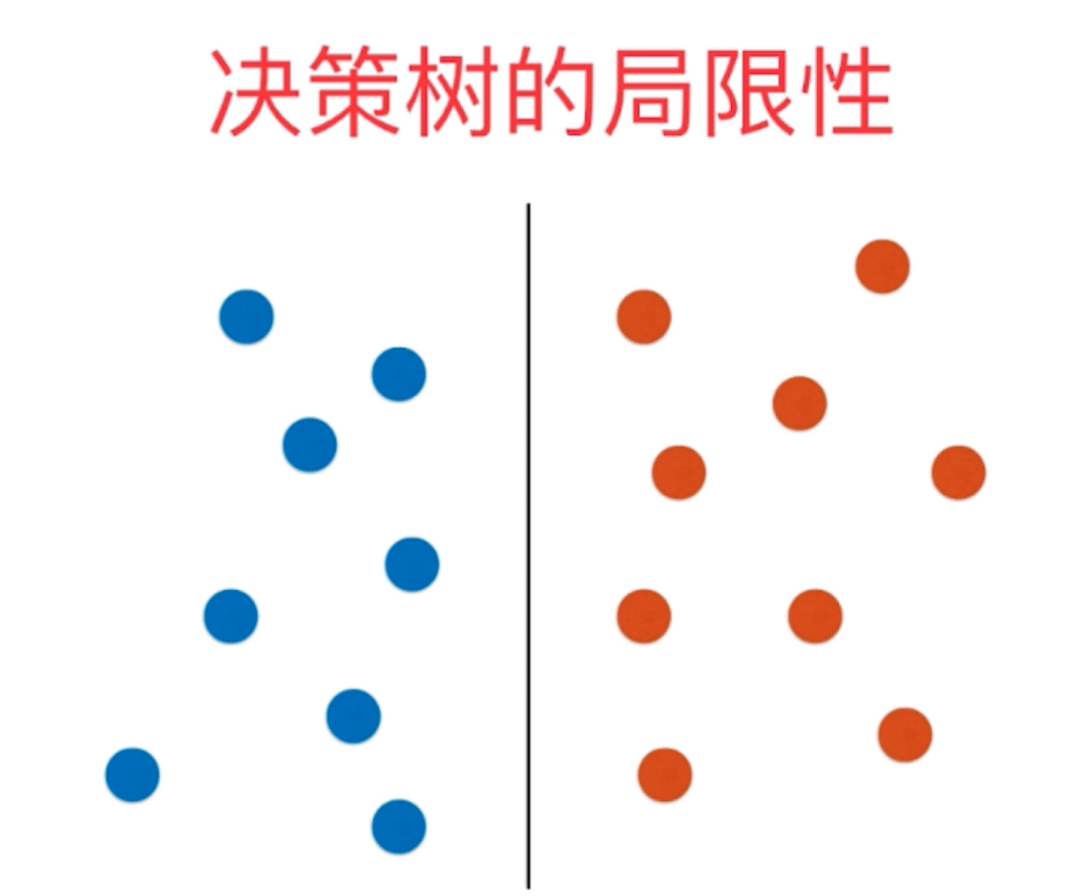
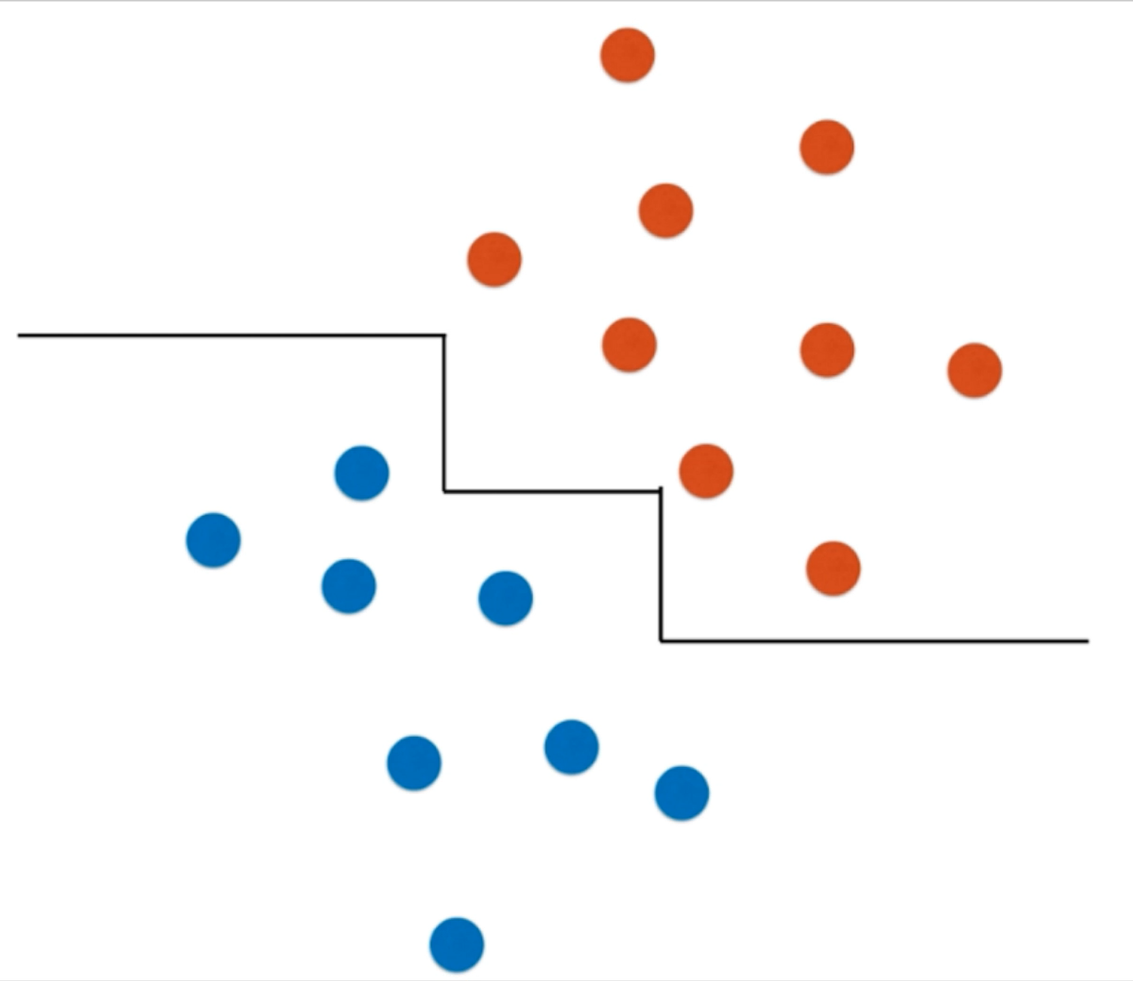
当数据分布由水平旋转一定的角之后，决策树的决策边界由竖直不能转变为倾斜的斜线，而只能变为锯齿线，并且在数据的左右两边决策边界由于训练数据量少的原因，形成了平行于x轴的决策边界，而这会造成很大的数据预测误差（因为两边数据可能是以斜线划分）。

 

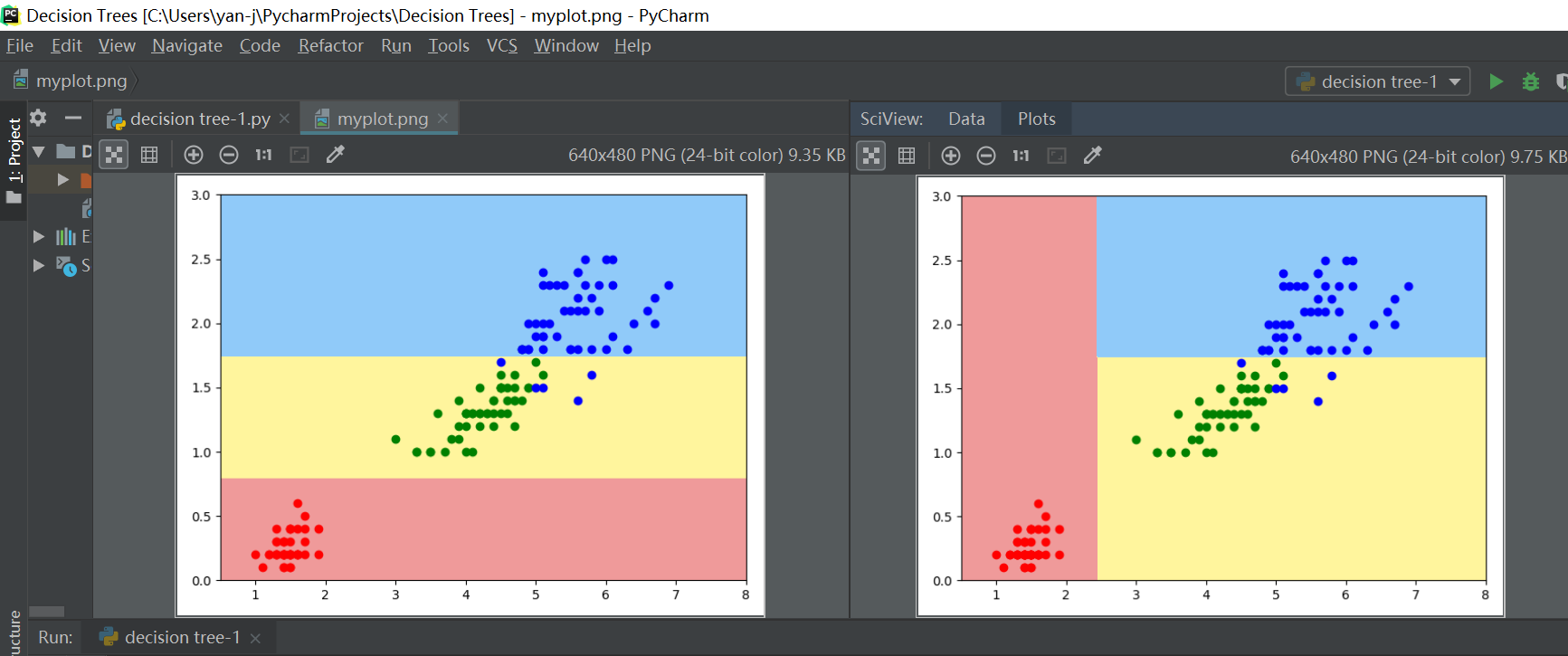
因为删除了训练数据集x的一个样本数据，造成了决策树决策边界非常大的变化。（非参数学习算法对于个别数据的高敏感性）