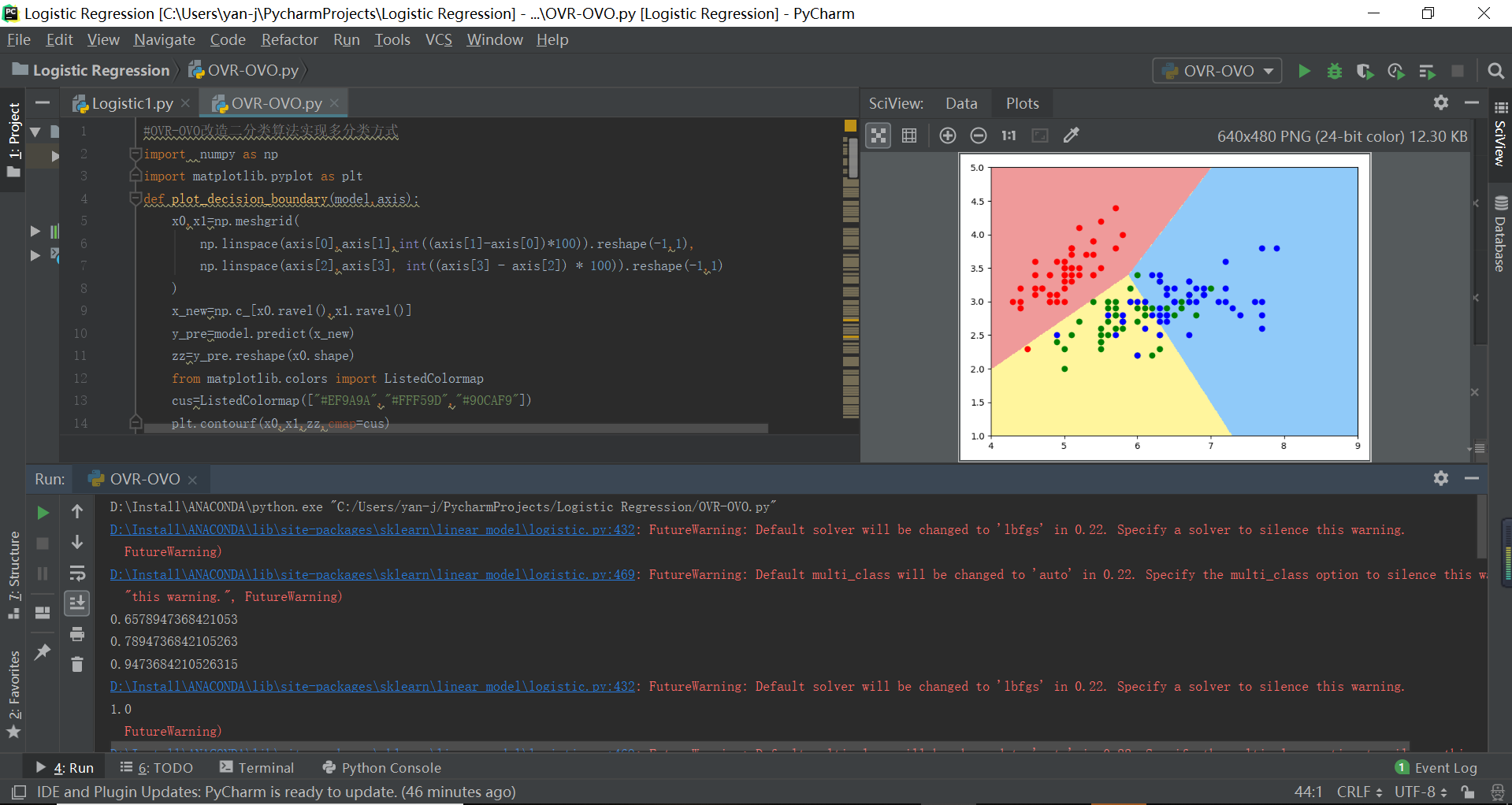
sklearn实现多分类逻辑回归
sklearn实现多分类逻辑回归
#二分类逻辑回归算法改造适用于多分类问题
1、对于逻辑回归算法主要是用回归的算法解决分类的问题,它只能解决二分类的问题,不过经过一定的改造便可以进行多分类问题,主要的改造方式有两大类:
(1)OVR/A(One VS Rest/ALL)
(2)OVO(One VS One)
2、对于OVR的改造方式,主要是指将多个分类结果(假设为n)分成是其中一种分类结果的和(其他),这样便可以有n种分类的模型进行训练,最终选择得分最高的的(预测率最高的的)便为分类结果即可。它所训练的时间是原来分类时间的n倍
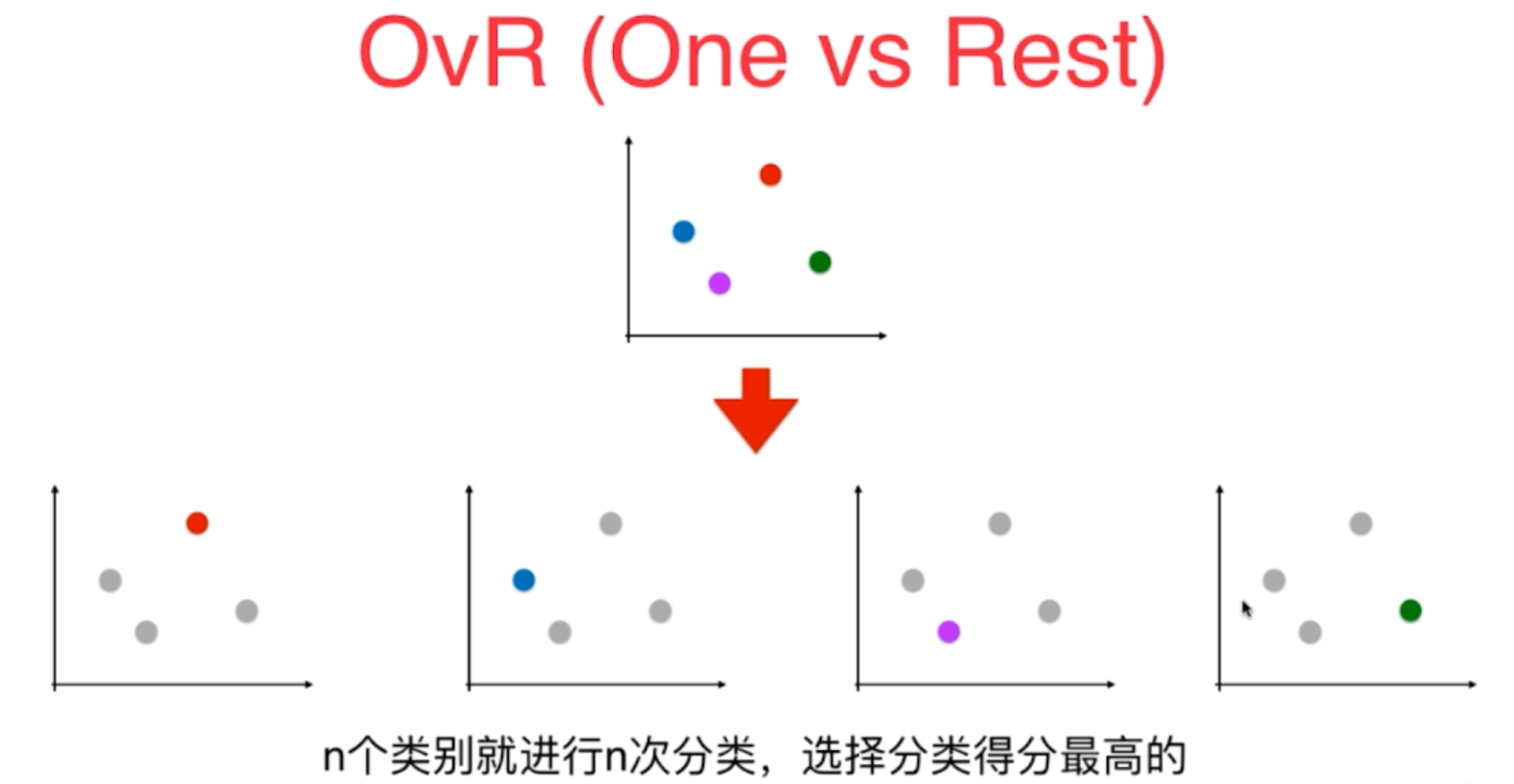
图1
3、对于OVO的方式,主要是将n个数据分类结果任意两个进行组合,然后对其单独进行训练和预测,最终在所有的预测种类中比较其赢数最高的即为分类结果,这样的分类方式最终将训练分为n(n-1)/2个模型,计算时间相对较长,不过这样的方式每次训练各个种类之间不混淆也不影响,因此比较准确。
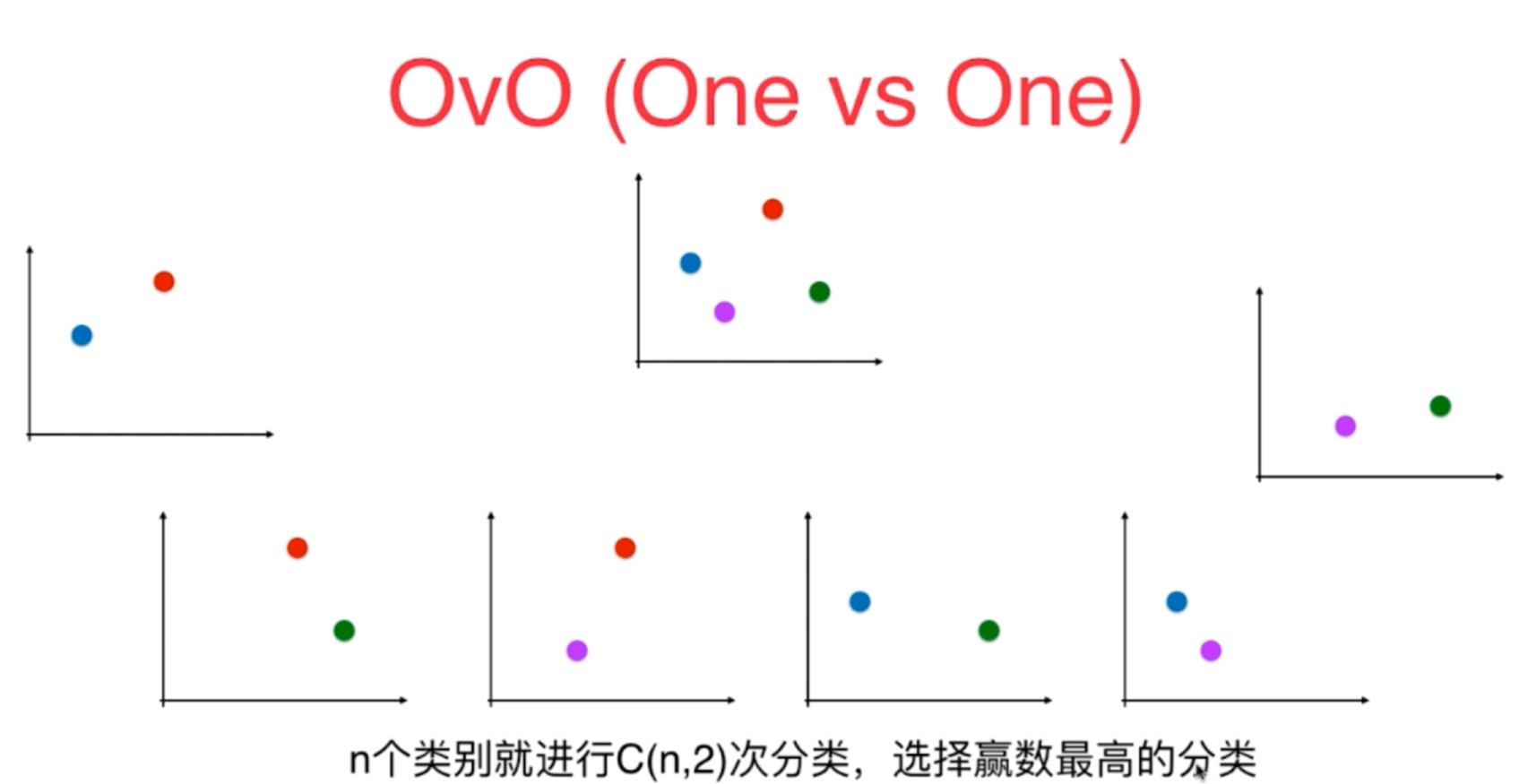
图2
4、sklearn中含有将逻辑回归进行多分类的函数封装,可以直接进行调用,当然也可以自己进行底层实现,都是比较方便的。在sklearn中实现逻辑回归的多分类任务具体实现代码如下所示:
#OVR-OVO改造二分类算法实现多分类方式
import numpy as np
import matplotlib.pyplot as plt
def plot_decision_boundary(model,axis): #两个数据特征基础下输出决策边界函数
x0,x1=np.meshgrid(
np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2],axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1,1)
)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_pre=model.predict(x_new)
zz=y_pre.reshape(x0.shape)
from matplotlib.colors import ListedColormap
cus=ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])
plt.contourf(x0,x1,zz,cmap=cus)
#采用iris数据集的两个数据特征进行模型训练与验证
from sklearn import datasets
d=datasets.load_iris()
x=d.data[:,:2] #选取特征数据集的前两个数据特征,方便输出决策出边界进行训练结果的对比
y=d.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.linear_model import LogisticRegression
#OVR方式的调用-默认方式
log_reg=LogisticRegression() #不输入参数时,默认情况下是OVR方式
log_reg.fit(x_train,y_train)
print(log_reg.score(x_test,y_test))
plot_decision_boundary(log_reg,axis=[4,9,1,5])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.scatter(x[y==2,0],x[y==2,1],color="b")
plt.show()
#OVO的方式进行逻辑回归函数参数的定义,结果明显好于OVR方式
log_reg1=LogisticRegression(multi_class="multinomial",solver="newton-cg")
log_reg1.fit(x_train,y_train)
print(log_reg1.score(x_test,y_test))
plot_decision_boundary(log_reg1,axis=[4,9,1,5])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.scatter(x[y==2,0],x[y==2,1],color="b")
plt.show()
#采用iris数据的所有特征数据
x=d.data
y=d.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.linear_model import LogisticRegression
#OVR方式的调用-默认胡方式
log_reg=LogisticRegression() #不输入参数时,默认情况下是OVR方式
log_reg.fit(x_train,y_train)
print(log_reg.score(x_test,y_test))
#采用OVO的方式进行逻辑回归函数参数的定义,结果明显好于OVR方式
log_reg1=LogisticRegression(multi_class="multinomial",solver="newton-cg")
log_reg1.fit(x_train,y_train)
print(log_reg1.score(x_test,y_test))
实现结果如下所示: