sklearn中的多项式回归算法
sklearn中的多项式回归算法
1、多项式回归法
多项式回归的思路和线性回归的思路以及优化算法是一致的,它是在线性回归的基础上在原来的数据集维度特征上增加一些另外的多项式特征,使得原始数据集的维度增加,然后基于升维后的数据集用线性回归的思路进行求解,从而得到相应的预测结果和各项的系数。
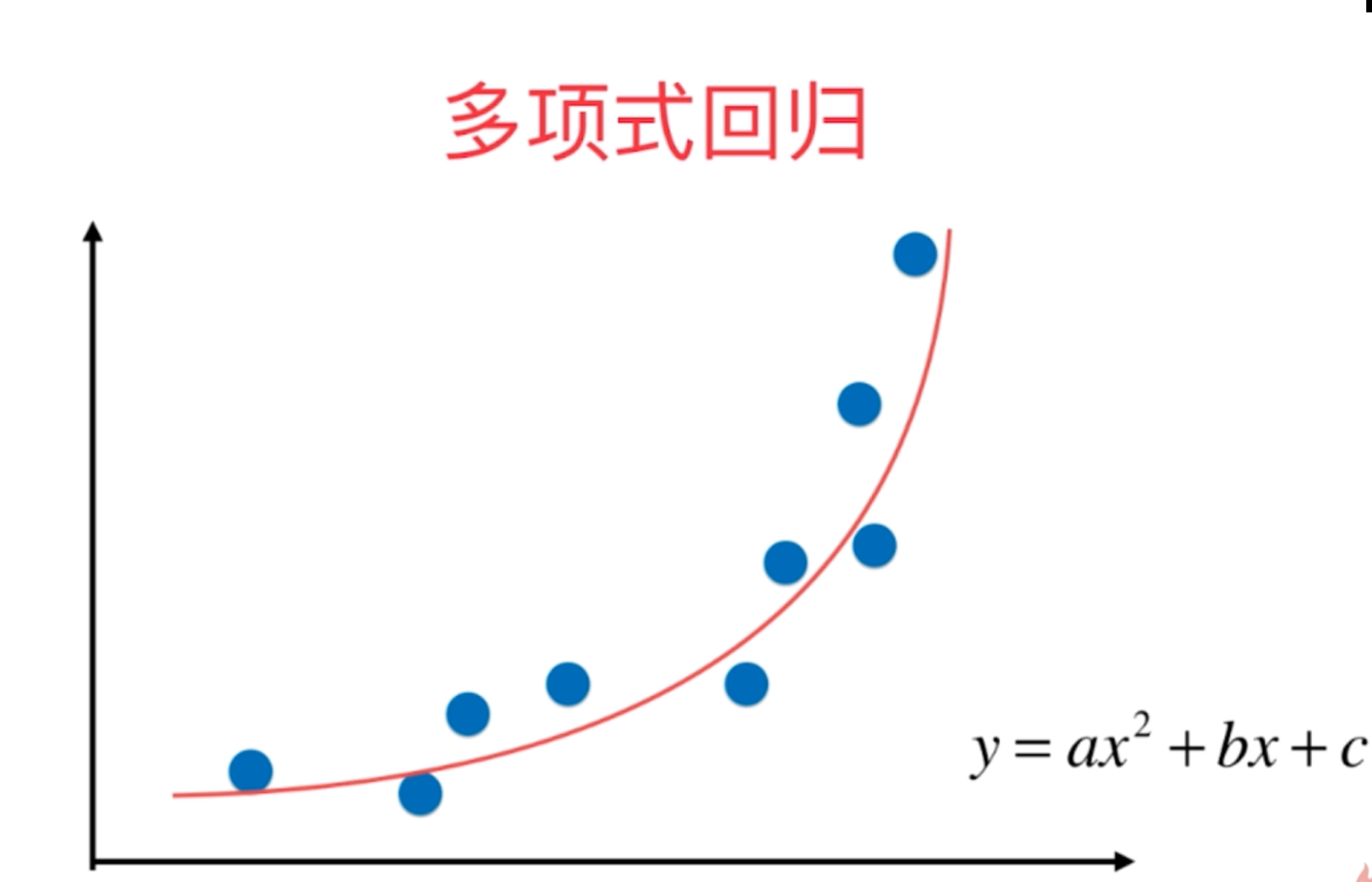
2、多项式回归的函数在pyhton的sklearn机器学习库中没有专门的定义,因为它只是线性回归方式的一种特例,但是我们自己可以按照多元线性回归的方式对整个过程进行相关的定义,然后包装成为一个函数进行相关的调用即可。
3、对于多项式回归方式的实现过程有以下两种:
(1)原理实现的过程代码(以一元二次函数的拟合为例):
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.figure()
plt.scatter(x,y)
from sklearn.linear_model import LinearRegression
l1=LinearRegression()
l1.fit(X,y)
y_p=l1.predict(X)
plt.plot(X,y_p,"r")
print(l1.score(X,y))
###1-1多项式回归的思路(使用线性回归的的思路,添加新的特征即可,即原数据集的维数增加)
print((x**2).shape)
x2=np.hstack([X,X**2])
print(x2.shape)
L2=LinearRegression()
L2.fit(x2,y)
y_p2=L2.predict(x2)
plt.figure()
plt.scatter(x,y)
plt.plot(X,y_p,"g")
plt.plot(np.sort(x),y_p2[np.argsort(x)],"r") #输出多维数据时的拟合结果
plt.show()
print(L2.score(x2,y))
print(L2.coef_,L2.intercept_)
(2)sklearn中的整体实现过程:
#sklearn中的多项式回归和pipeline
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
from sklearn.preprocessing import PolynomialFeatures
p1=PolynomialFeatures(degree=2) #degree的含义是多项式数据中添加特征的最高次数
p1.fit(X)
x3=p1.transform(X)
print(x3.shape)
print(x3[:5,0])
print(x3[:5,1])
print(x3[:5,2])
print(x3[:5,])
from sklearn.linear_model import LinearRegression
l3=LinearRegression()
l3.fit(x3,y)
y_p3=l3.predict(x3)
plt.figure()
plt.scatter(x,y)
plt.plot(np.sort(x),y_p3[np.argsort(x)],"r")
plt.show()
print(l3.score(x3,y))
print(l3.coef_,L2.intercept_)
print(x3.shape)
(3)利用上述原理进行函数的自我封装调用代码:
#自己封装一个多项式回归的函数
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
def polynomialRegression(degree):
return Pipeline([("poly",PolynomialFeatures(degree=degree)),
("std_scaler",StandardScaler()),
( "lin_reg",LinearRegression())
])
poly2_reg=polynomialRegression(10)
poly2_reg.fit(X,y)
y2=poly2_reg.predict(X)
print(mean_squared_error(y,y2))
print(poly2_reg.score(X,y))
plt.figure()
plt.scatter(X,y)
plt.plot(np.sort(x),y2[np.argsort(x)],"r")
plt.show()
x1=np.linspace(-3,3,100).reshape(100,1)
y11=poly2_reg.predict(x1)
plt.plot(x1,y11,"r")
#plt.axis([-3,3,-1,10])
plt.show()
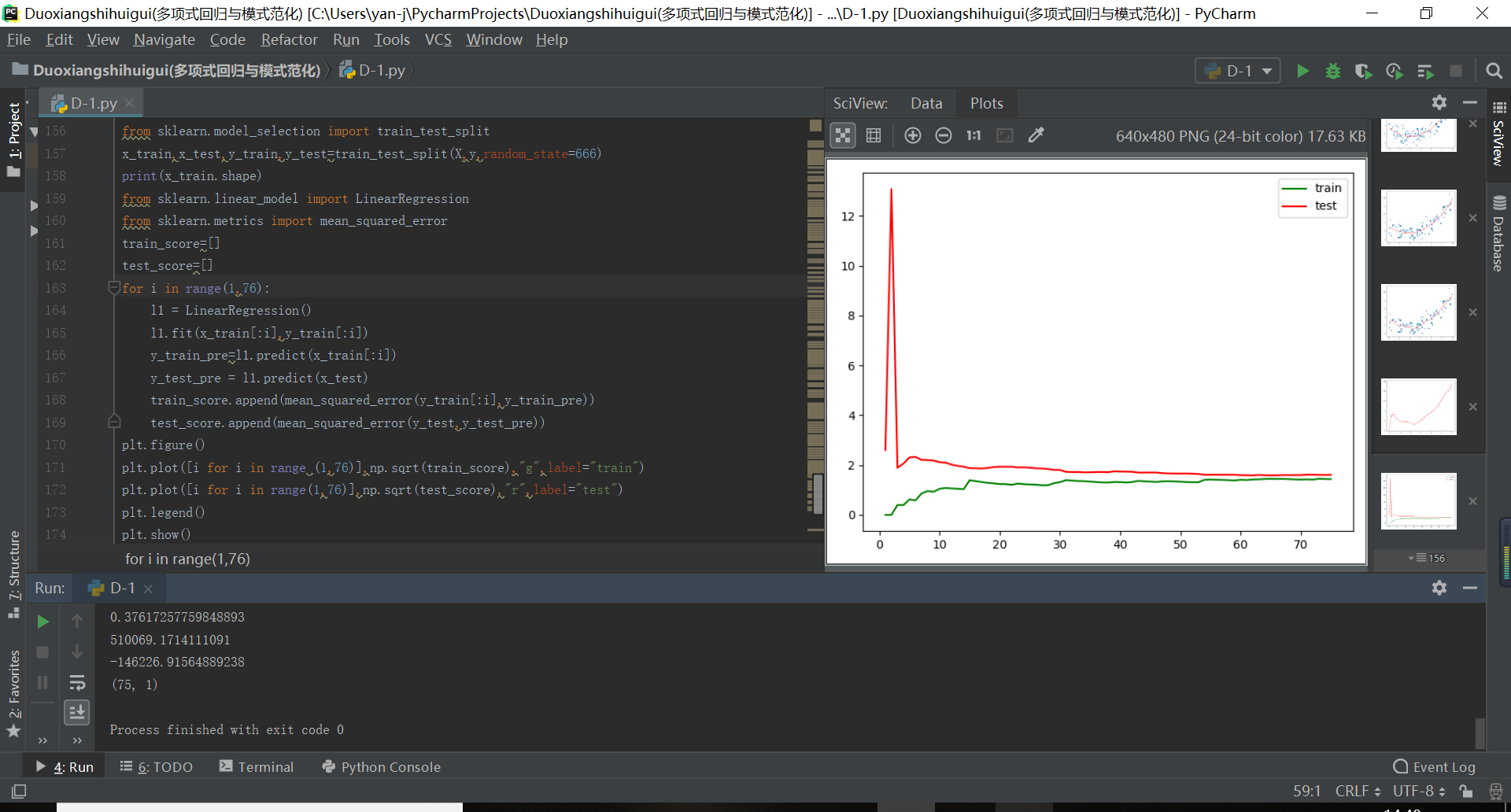
运行结果如下所示: